当前位置： 首页 > news >正文

[BUG记录]UART占用CPUload过高问题

news 2026/2/9 22:58:11

目录

  • 关键词
  • 平台说明
  • 一、背景
  • 二、根本原因
  • 三、措施

  

关键词

嵌入式、C语言、autosar、TDA4

平台说明

项目Value
OSautosar OS
autosar厂商vector
芯片厂商TI
编程语言C，C++
编译器HighTec (GCC)

一、背景

  在基于TDA4开发的域控中使用到了UART打印debug信息，不管是A核还是R核都用到了。但是发现CPUload异常升高。

二、根本原因

  因为使用到了UART的同步打印，导致系统等待时间过长，消耗了不必要的资源。

三、措施

  改为异步打印，减少不必要的debug内容。

相关文章：

[BUG记录]UART占用CPUload过高问题

目录 关键词平台说明一、背景二、根本原因三、措施 关键词 嵌入式、C语言、autosar、TDA4 平台说明 项目ValueOSautosar OSautosar厂商vector芯片厂商TI编程语言C，C编译器HighTec (GCC) 一、背景 在基于TDA4开发的域控中使用到了UART打印debug信息，不…...

编程日记 2023/12/14 7:10:05

Flutter常用命令

一、环境安装 flutter --version 查看当前安装的flutter 版本 flutter upgrade 升级当前的flutter 版本 flutter doctor 检查环境安装是否完成 二、项目编译运行 flutter clean 清空build目录 flutter pub get 获取pub插件包 flutter run --设备名称 运行项目到指定设…...

编程日记 2023/12/14 7:02:58

【C++】POCO学习总结（十四）：引用计数、共享指针、缓冲区管理

【C】郭老二博文之：C目录 1、Poco::AutoPtr 智能指针 1.1 说明 Poco::AutoPtr是一个含有引用计数的“智能”指针模版。 Poco::AutoPtr用于支持引用计数的类实例化。支持引用计数的类需要有以下要求： 维护一个引用计数(在创建时初始化为1)实现void du…...

编程日记 2023/12/14 7:01:57

Python之禅

import this 这是 Python 社区中著名的 "The Zen of Python"（Python之禅）文档，由 Python 创始人之一的 Tim Peters 撰写。这个文档包含了一系列关于编程和代码设计哲学的原则，以指导 Python 社区的开发者。以下是这些原…...

编程日记 2023/12/14 7:00:57

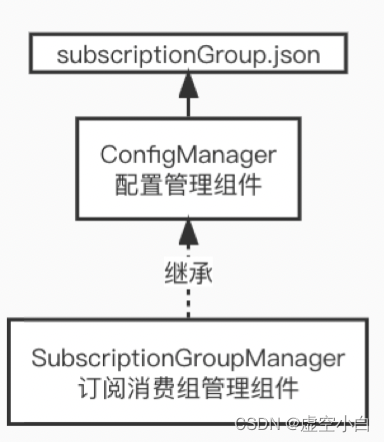
RocketMQ源码 Broker-SubscriptionGroupManager 订阅组管理组件源码分析

前言 SubscriptionGroupManager 继承了ConfigManager配置管理组件，拥有将内存数据持久化到磁盘文件subscriptionGroup.json的能力。它主要负责维护所有消费组在内存中的订阅数据。 源码版本：4.9.3 源码架构图 核心数据结构 主要的数据结构比较简单&am…...

编程日记 2023/12/14 6:59:55

go-zero开发入门-API网关鉴权开发示例

本文是go-zero开发入门-API网关开发示例一文的延伸，继续之前请先阅读此文。 在项目根目录下创建子目录 middleware，在此目录下创建文件 auth.go，内容如下： // 鉴权中间件 package middlewareimport ("context""e…...

编程日记 2023/12/14 6:56:53

[LLM]nanoGPT---训练一个写唐诗的GPT

karpathy/nanoGPT: The simplest, fastest repository for training/finetuning medium-sized GPTs. (github.com) 原有模型使用的莎士比亚的戏剧数据集, 如果需要一个写唐诗机器人，需要使用唐诗的文本数据， 一个不错的唐诗，宋词数据的下载…...

编程日记 2023/12/14 6:55:53

docker compose部署wordpress

准备机器： 192.168.58.151 （关闭防火墙和selinux） 安装好docker服务 （详细参照：http://t.csdnimg.cn/usG0s 中的国内源安装docker） 部署wordpress: 创建目录： [rootdocker ~]# mkdir…...

编程日记 2023/12/14 6:54:52

【docker四】使用Docker-compose一键部署Wordpress平台

目录 一、YAML 文件格式及编写注意事项（重要） 1、yaml文件使用时注意事项： 2、yaml文件的基本数据结构： 2.1、声明变量（标量。是单个的不可再分的值，类型：字符串，整数&#xff0c…...

编程日记 2023/12/14 6:48:47

HTML程序大全(1)：简易计算器

HTML代码&#xff0c;主要创建了几个按钮。 <div class"container"><div class"output" id"output">0</div><button class"button" onclick"clearOutput()" id"clear">C</button>…...

编程日记 2023/12/14 6:46:45

esp32服务器与android客户端的tcp通讯

esp32 //esp32作为服务端 #include <WiFi.h>#define LED_BUILTIN 2 // 创建热点 const char *ssid "ESP32"; const char *password "12345678"; const int port 1122; //端口 WiFiServer server(port); void setup() {delay(5000);pinMode(LED_…...

编程日记 2023/12/14 6:44:44

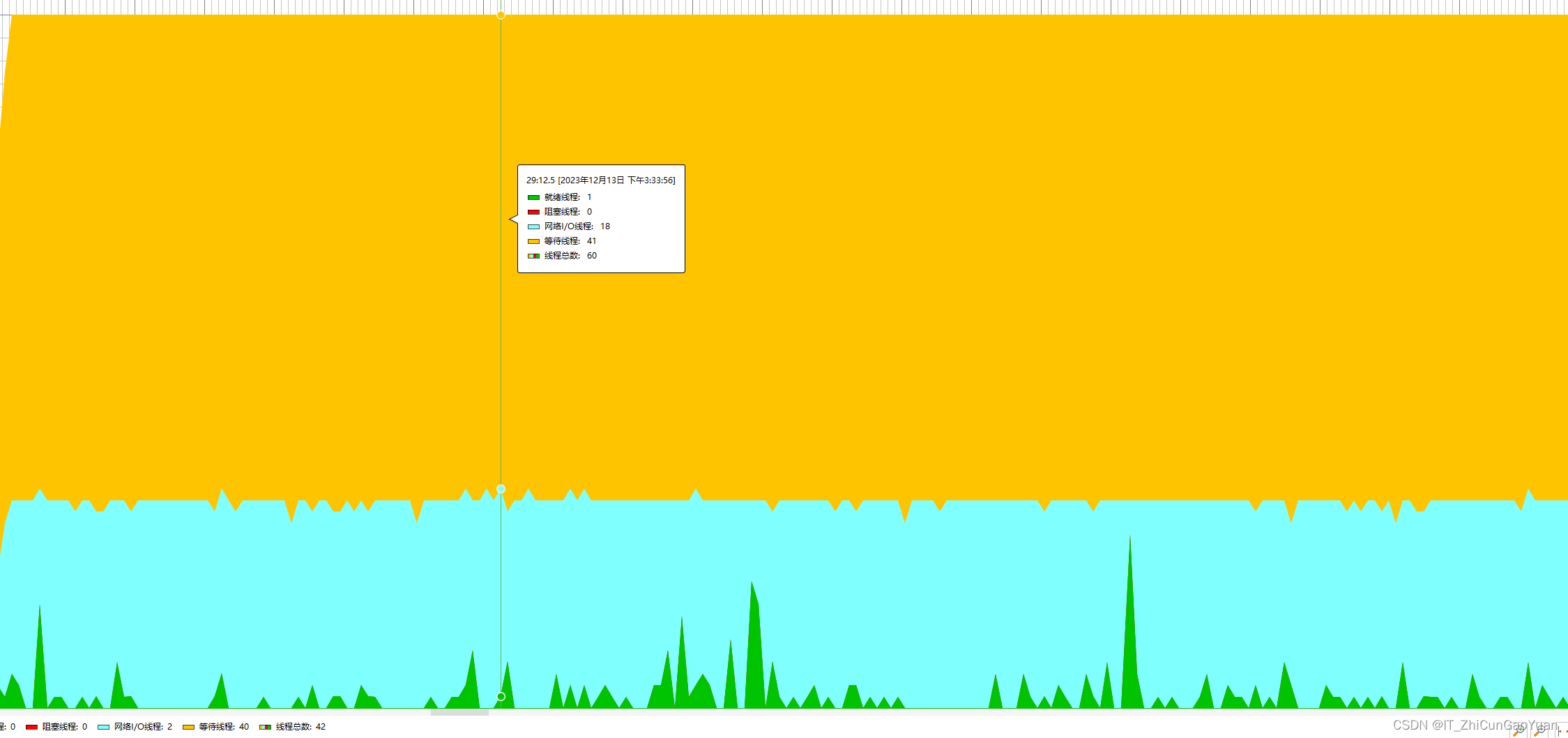
自定义Mybatis LanguageDriver性能优化

场景&#xff1a;高并发情况下mybatis 动态sql 解析 锁问题优化 优化前 并发测试 XMLLanguageDriver 类 的 createSqlSource 方法有锁 而且 每次执行时都会走该方法 优化前 &#xff1a; 线程有Block 优化后的 LanguageDriver public class CustomXMLLanguageDriver im…...

编程日记 2023/12/14 6:41:41

DevEco Studio 鸿蒙（HarmonyOS）项目结构

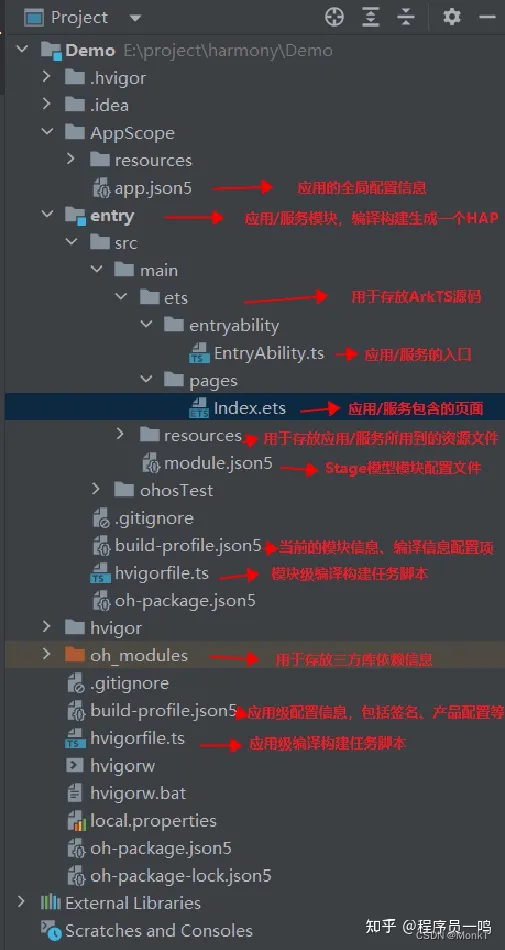
DevEco Studio 鸿蒙&#xff08;HarmonyOS&#xff09;项目结构 一、操作环境 操作系统: Windows 10 专业版 IDE:DevEco Studio 3.1 SDK:HarmonyOS 3.1 二、项目结构 创建简单的Hello World移动应用项目结构如下图 由上到下说明各个文件夹的作用 .hvigor&#xff1a;存…...

编程日记 2023/12/14 6:38:39

Springboot整合篇Druid

一、概述 1.1简介 Druid 是阿里巴巴开源平台上一个数据库连接池实现&#xff0c;结合了 C3P0、DBCP 等 DB 池的优点&#xff0c;同时加入了日志监控。 它本身还自带一个监控平台&#xff0c;可以查看时时产生的sql、uri等监控数据&#xff0c;可以排查慢sql、慢请求&#xff0…...

编程日记 2023/12/14 6:36:37

uniapp 微信小程序 封装axios 包含请求拦截、响应拦截、无感刷新令牌功能

前言&#xff1a; 1、为什么不适用uniapp自带的请求功能&#xff1f; 答&#xff1a;uniapp自带的请求功能&#xff0c;再刷新了令牌后&#xff0c;重新请求返回的数据无法返回给发起请求的方法。也就是说&#xff0c;刷新令牌后重新发起的请求和第一次发起请求的方法是割裂的。…...

编程日记 2023/12/14 6:34:36

C语言精选——选择题Day41

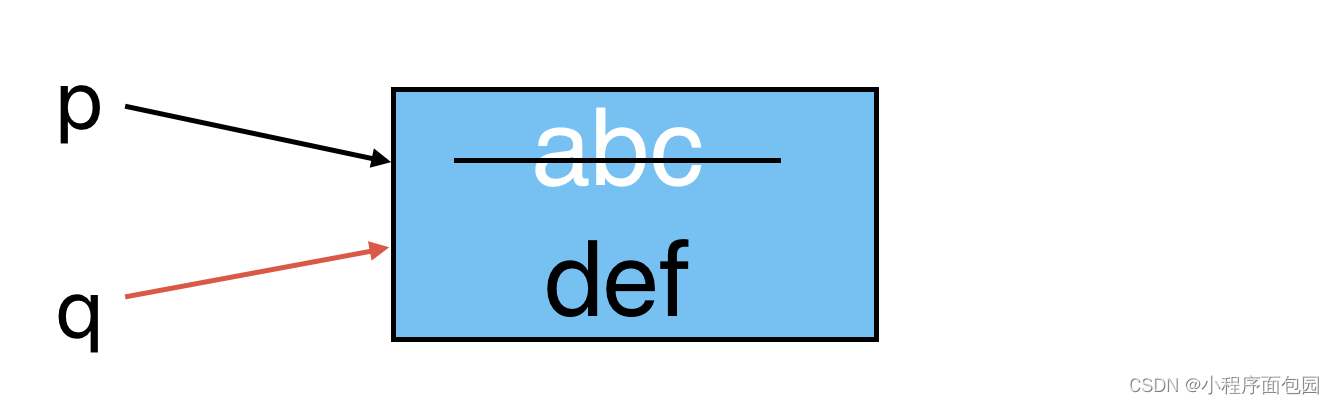
第一题 1. 有以下程序段&#xff1a; char *p, *q; p (char *)malloc(sizeof(char) * 20); q p; scanf("%s %s", p, q); printf("%s %s\n", p, q); 若从键盘输入&#xff1a;abc def↙&#xff0c;则输出结果是&#xff08; &#xff09; A&#xff1a;d…...

编程日记 2023/12/14 6:33:35

Tomcat头上有个叉叉

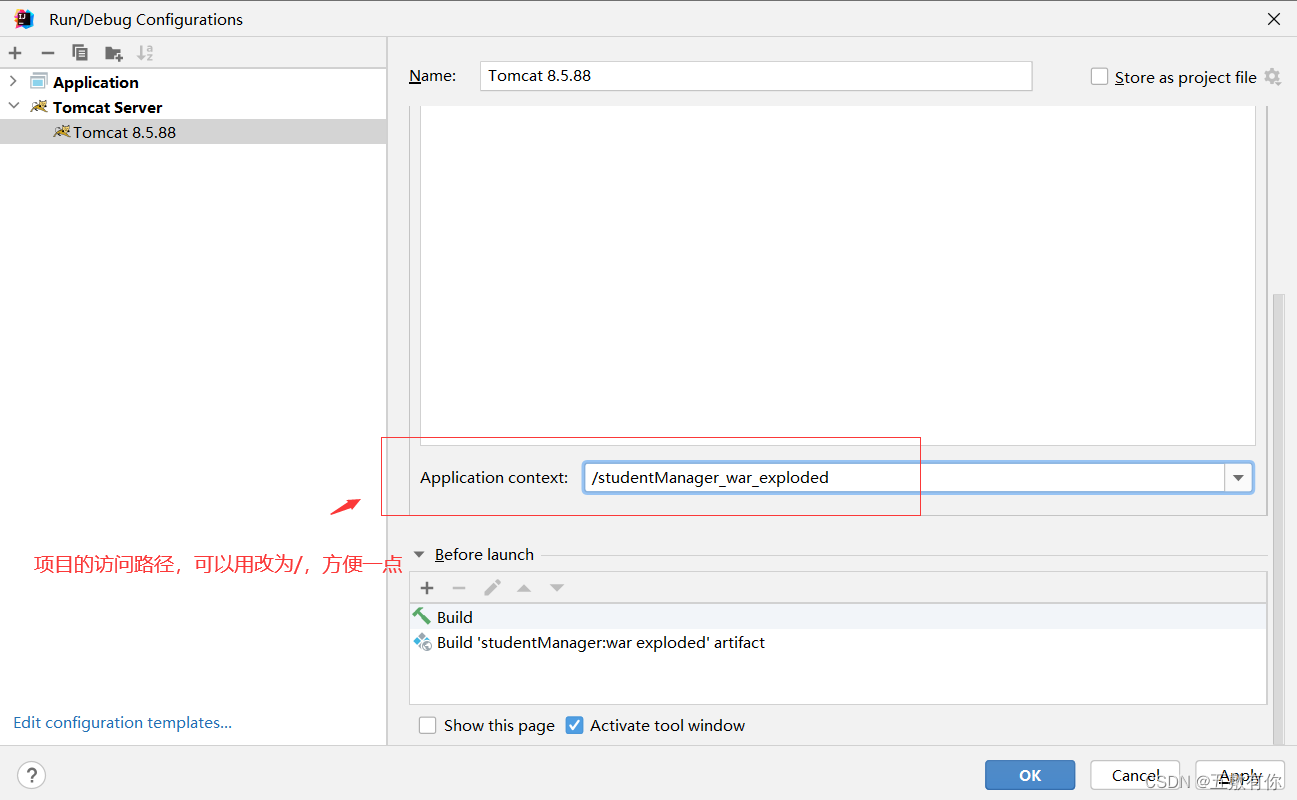
问题原因&#xff1a; 这是因为它就是个空的tomcat,并没有导入项目运行 解决方案&#xff1a; war模式&#xff1a;发布模式&#xff0c;正式发布时用&#xff0c;将WEB工程以war包的形式上传到服务器 war exploded模式&#xff1a;开发时用&#xff0c;将WEB工程的文件夹直接…...

编程日记 2023/12/14 6:32:34

Linux shell编程学习笔记35：seq

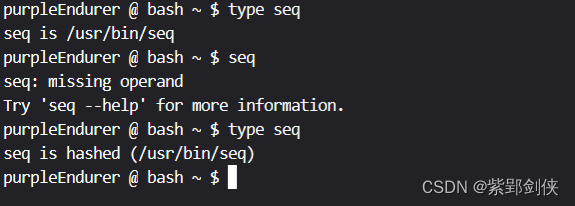
0 前言 在使用 for 循环语句时&#xff0c;我们经常使用到序列。比如&#xff1a; for i in 1 2 3 4 5 6 7 8 9 10; do echo "$i * 2 $(expr $i \* 2)"; done 其中的 1 2 3 4 5 6 7 8 9 10;就是一个整数序列 。 为了方便我们使用数字序列&#xff0c;Linux提供了…...

编程日记 2023/12/14 6:29:32

Nougat：结合光学神经网络，引领学术PDF文档的智能解析、挖掘学术论文PDF的价值

Nougat&#xff1a;结合光学神经网络&#xff0c;引领学术PDF文档的智能解析、挖掘学术论文PDF的价值 这是Nougat的官方存储库&#xff0c;Nougat是一种学术文档PDF解析器&#xff0c;可以理解LaTeX数学和表格。 Project page: https://facebookresearch.github.io/nougat/ …...

编程日记 2023/12/14 6:28:31

涉密网络的IP查询防护策略

涉密网络的安全性对于维护国家、企业及个人的核心利益至关重要。在当今数字化时代&#xff0c;网络攻击日益猖獗&#xff0c;其中IP查询是攻击者获取目标信息的一种常见手段。本文将探讨涉密网络中防护IP查询的关键策略&#xff0c;以确保网络的机密性和安全性。 1. 专用VPN和…...

编程日记 2023/12/14 6:27:30

MPNet：旋转机械轻量化故障诊断模型详解python代码复现

目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块（MBFM） 2.2 残差注意力金字塔模块（RAPM） 2.2.1 空间金字塔注意力（SPA） 2.2.2 金字塔残差块（PRBlock） 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

编程新知 2026/2/7 5:16:28

【JVM】- 内存结构

引言 JVM&#xff1a;Java Virtual Machine 定义&#xff1a;Java虚拟机&#xff0c;Java二进制字节码的运行环境好处&#xff1a; 一次编写&#xff0c;到处运行自动内存管理&#xff0c;垃圾回收的功能数组下标越界检查&#xff08;会抛异常&#xff0c;不会覆盖到其他代码…...

编程新知 2026/1/30 13:40:43

UDP(Echoserver)

网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法&#xff1a;netstat [选项] 功能&#xff1a;查看网络状态 常用选项&#xff1a; n 拒绝显示别名&#…...

编程新知 2026/1/24 7:56:15

1688商品列表API与其他数据源的对接思路

将1688商品列表API与其他数据源对接时&#xff0c;需结合业务场景设计数据流转链路&#xff0c;重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点&#xff1a; 一、核心对接场景与目标 商品数据同步 场景&#xff1a;将1688商品信息…...

编程新知 2025/11/30 16:55:32

OPENCV形态学基础之二腐蚀

一.腐蚀的原理 (图1) 数学表达式&#xff1a;dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一&#xff0c;腐蚀跟膨胀属于反向操作&#xff0c;膨胀是把图像图像变大&#xff0c;而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

编程新知 2026/2/8 22:00:17

安卓基础（aar）

重新设置java21的环境&#xff0c;临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的&#xff1a; MyApp/ ├── app/ …...

编程新知 2026/1/25 8:10:56

智能AI电话机器人系统的识别能力现状与发展水平

一、引言 随着人工智能技术的飞速发展&#xff0c;AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术&#xff0c;在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

编程新知 2025/6/11 3:05:02

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档&#xff09;&#xff0c;如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下&#xff0c;风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

编程新知 2026/2/9 17:44:07

SQL慢可能是触发了ring buffer

简介 最近在进行 postgresql 性能排查的时候，发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升，且低水位伴随在整个慢 SQL，一直是 buferIO 的等待事件，此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ，但…...

编程新知 2025/10/2 9:17:52

FFmpeg：Windows系统小白安装及其使用

一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】&#xff0c;注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录&#xff08;即exe所在文件夹&#xff09;加入系统变量…...

编程新知 2026/1/31 14:34:46