ARM流水灯
.text
.global _start
_start:
@LED1
@1.RCC时钟使能GPIOE RCC_MP_AHB4ENSETR[4]->1
LDR R0,=0x50000a28
LDR R1,[R0]
ORR R1,R1,#(0x1<<4)
STR R1,[R0]
@2.设置PE10为输出模式 GPIOE_MODER[21:20]->01
@先清0
LDR R0,=0x50006000
LDR R1,[R0]
BIC R1,R1,#(0x3<<20)
@再置位
ORR R1,R1,#(0x1<<20)
STR R1,[R0]
@3.设置PE10为推挽输出 GPIOE_OTYPER[10]->0
LDR R0,=0x50006004
LDR R1,[R0]
BIC R1,R1,#(0x1<<10)
STR R1,[R0]
@4.设置PE10为低速输出 GPIOE_OSPEEDR[21:20]->00
LDR R0,=0x50006008
LDR R1,[R0]
BIC R1,R1,#(0x3<<20)
STR R1,[R0]
@5.设置PE10输出无上拉下拉 GPIOE_PUPDR[21:20]->00
LDR R0,=0x5000600C
LDR R1,[R0]
BIC R1,R1,#(0x3<<20)
STR R1,[R0]
@LED2
@1.RCC时钟使能GPIOE RCC_MP_AHB4ENSETR[5]->1
LDR R0,=0x50000a28
LDR R1,[R0]
ORR R1,R1,#(0x1<<5)
STR R1,[R0]
@2.设置PF10为输出模式 GPIOF_MODER[21:20]->01
@先清0
LDR R0,=0x50007000
LDR R1,[R0]
BIC R1,R1,#(0x3<<20)
@再置位
ORR R1,R1,#(0x1<<20)
STR R1,[R0]
@3.设置PF10为推挽输出 GPIOF_OTYPER[10]->0
LDR R0,=0x50007004
LDR R1,[R0]
BIC R1,R1,#(0x1<<10)
STR R1,[R0]
@4.设置PF10为低速输出 GPIOF_OSPEEDR[21:20]->00
LDR R0,=0x50007008
LDR R1,[R0]
BIC R1,R1,#(0x3<<20)
STR R1,[R0]
@5.设置PF10输出无上拉下拉 GPIOF_PUPDR[21:20]->00
LDR R0,=0x5000700C
LDR R1,[R0]
BIC R1,R1,#(0x3<<20)
STR R1,[R0]
@LED3
@1.RCC时钟使能GPIOE RCC_MP_AHB4ENSETR[4]->1
LDR R0,=0x50000a28
LDR R1,[R0]
ORR R1,R1,#(0x1<<4)
STR R1,[R0]
@2.设置PE8为输出模式 GPIOE_MODER[17:16]->01
@先清0
LDR R0,=0x50006000
LDR R1,[R0]
BIC R1,R1,#(0x3<<16)
@再置位
ORR R1,R1,#(0x1<<16)
STR R1,[R0]
@3.设置PE8为推挽输出 GPIOE_OTYPER[8]->0
LDR R0,=0x50006004
LDR R1,[R0]
BIC R1,R1,#(0x1<<8)
STR R1,[R0]
@4.设置PE8为低速输出 GPIOE_OSPEEDR[17:16]->00
LDR R0,=0x50006008
LDR R1,[R0]
BIC R1,R1,#(0x3<<16)
STR R1,[R0]
@5.设置PE8输出无上拉下拉 GPIOE_PUPDR[17:16]->00
LDR R0,=0x5000700C
LDR R1,[R0]
BIC R1,R1,#(0x3<<16)
STR R1,[R0]@LED1闪烁
loop:
@LED1亮
BL led1_on
bl delay
@LED1灭
BL led1_off
bl delay
@LED2亮
BL led2_on
bl delay
@LED2灭
BL led2_off
bl delay
@LED3亮
BL led3_on
bl delay
@LED2灭
BL led3_off
bl delayb loop@LED1亮
led1_on:LDR R0,=0x50006014LDR R1,[R0]ORR R1,R1,#(0x1<<10)STR R1,[R0] mov pc,lr
@LED1灭
led1_off:LDR R0,=0x50006014LDR R1,[R0]BIC R1,R1,#(0x1<<10)STR R1,[R0] mov pc,lr
@LED2亮
led2_on:LDR R0,=0x50007014LDR R1,[R0]ORR R1,R1,#(0x1<<10)STR R1,[R0] mov pc,lr
@LED2灭
led2_off:LDR R0,=0x50007014LDR R1,[R0]BIC R1,R1,#(0x1<<10)STR R1,[R0] mov pc,lr
@LED3亮
led3_on:LDR R0,=0x50006014LDR R1,[R0]ORR R1,R1,#(0x1<<8)STR R1,[R0] mov pc,lr
@LED3灭
led3_off:LDR R0,=0x50006014LDR R1,[R0]BIC R1,R1,#(0x1<<8)STR R1,[R0] mov pc,lr@封装汇编的延时函数
delay:LDR R1,=0X10000000
mm:cmp R1,#0SUBNE R1,R1,#1BNE mmmov pc,lr.end
LDE1:

LED2:

LED3:

相关文章:

ARM流水灯
.text .global _start _start: LED1 1.RCC时钟使能GPIOE RCC_MP_AHB4ENSETR[4]->1 LDR R0,0x50000a28 LDR R1,[R0] ORR R1,R1,#(0x1<<4) STR R1,[R0] 2.设置PE10为输出模式 GPIOE_MODER[21:20]->01 先清0 LDR R0,0x50006000 LDR R1,[R0] BIC R1,R1,#(0x3<&…...

docker-compose单机容器编排
Dockerfile:先配置好文件,然后build,镜像-------->容器。 docker-conpose 既可以基于dockerfile,也可以基于镜像,一键式拉起镜像和容器。 docker-compose核心就是yml文件,可以定义容器的一切。通过yml配置,直接运行…...

matlab信号分选系统算法-完整算法结构
matlab信号分选系统算法 针对得到的脉冲流PDW进行信号分选,包括重频恒定、重频抖动、重频参差和重频滑变四种脉间调制类型。 这里我们先进行数据的仿真,后续边仿真边分享思路:首先根据信号类型,分别产生重频恒定、重频抖动、重…...
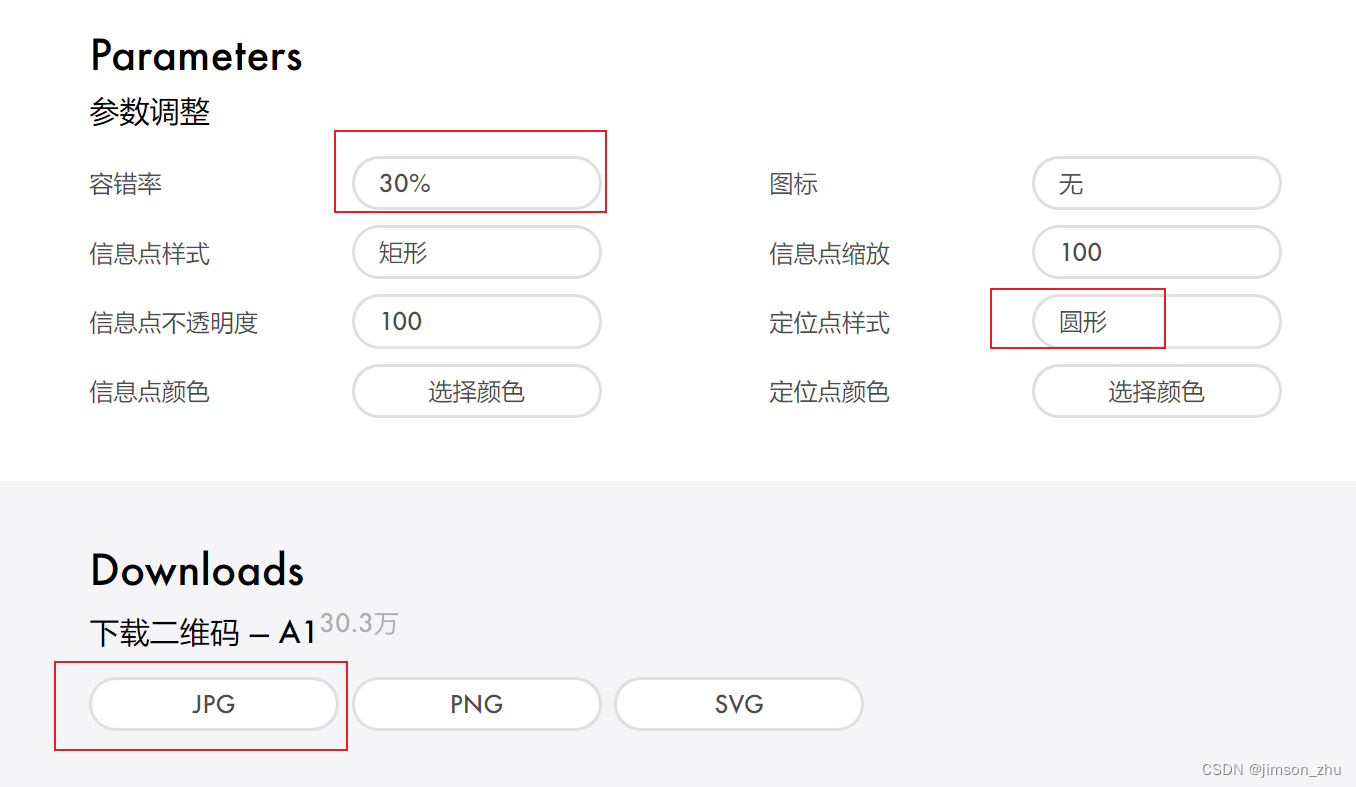
十八)Stable Diffusion使用教程:艺术二维码案例
今天说说怎么样使用SD生成艺术二维码。 我们直接上图。 方式有三种,分别如下: 1)方式一:直接 contronet 的tile模型进行控制 使用QRBTF Classic生成你的二维码。 首先输入网址,选择喜欢的二维码样式(推荐第一种就行): 然后选择相应参数,这里推荐最大的容错率,定…...

【LeetCode每日一题】53. 最大子数组和
https://leetcode.cn/problems/maximum-subarray/description/ 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 方式一:暴力…...

机器学习笔记 什么是协方差矩阵?
一、协方差矩阵 协方差矩阵是一种矩阵,用于表示随机向量中给定的元素对之间的协方差值。协方差矩阵也可以称为色散矩阵或方差-协方差矩阵。这是因为每个元素的方差是沿着矩阵的主对角线表示的。 协方差矩阵始终是方阵。此外,它是半正定且对称的。该矩阵在随机建模和主成分分析…...
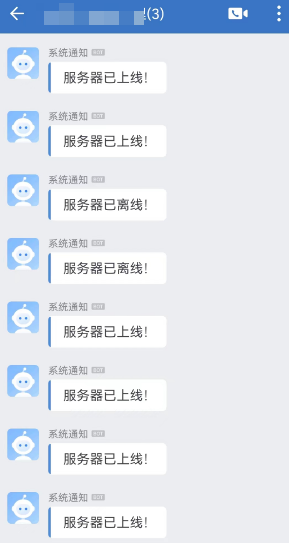
使用Python监控服务器在线状态
前言 在公司内网有一台服务器,有动态的公网IP,使用DDNS对外提供服务,但是会因为停电、服务器卡死等原因导致服务器离线。服务器离线后无法及时获知,因此需要实现在服务器离线的时候能够发送消息到手机上。 思路梳理 公司办理的…...
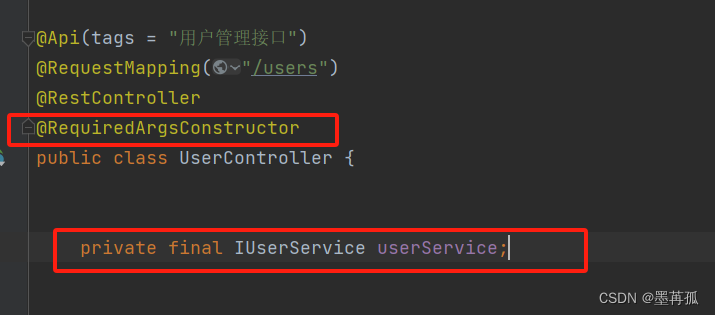
【JAVA】黑马MybatisPlus 学习笔记【二】【核心功能】
2.核心功能 刚才的案例中都是以id为条件的简单CRUD,一些复杂条件的SQL语句就要用到一些更高级的功能了。 2.1.条件构造器 除了新增以外,修改、删除、查询的SQL语句都需要指定where条件。因此BaseMapper中提供的相关方法除了以id作为where条件以外&…...
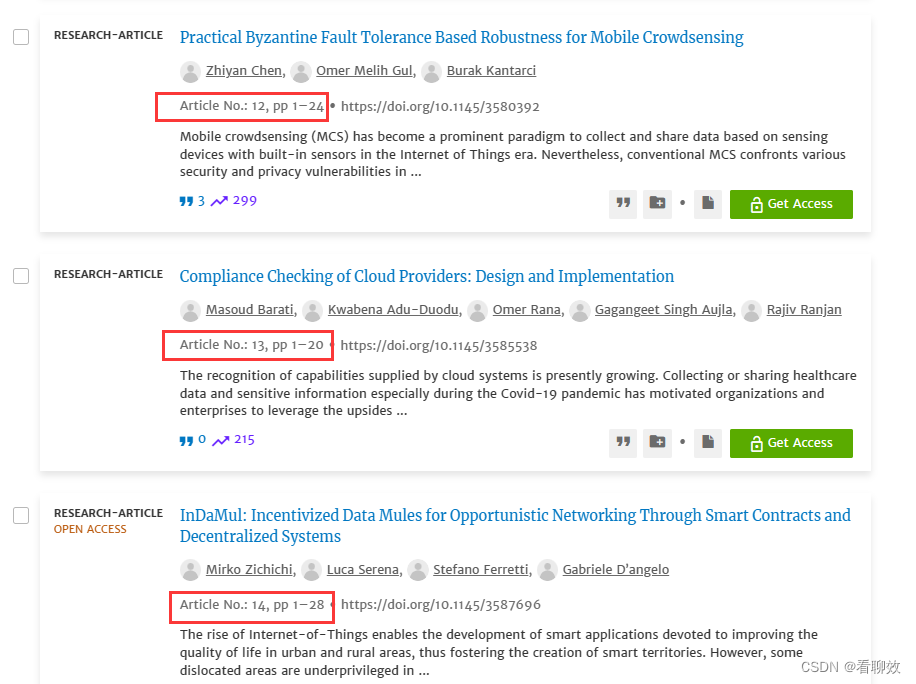
区块链实验室(30) - 区块链期刊:Distributed Ledger Technologies: Research and Practice
区块链涉及多学科及技术,众多期刊接收区块链文章。Distributed Ledger Technologies: Research and Practice是ACM出版集团的一本期刊。 Distributed Ledger Technologies: Research and Practice创刊历史很短,始于2022年,出版期数也不多。 载…...

Nginx【通俗易懂】《中篇》
目录 1.Url重写rewrite 2.防盗链 3.静态资源压缩 4.跨域问题 1.Url重写rewrite 🤩🤩🤩 1.1.rewrite书写格式 rewrite是实现URL重写的关键指令,根据regex(正则表达式)部分内容,重定向到rep…...

组件的二次封装
在React中,使用扩展运算符(...)来传递props的作用是将一个对象的所有可枚举属性(包括自身的和继承的)复制到新创建的对象中。当我们在二次封装组件时使用它,可以方便地将所有传递给我们的props传递给基础组…...
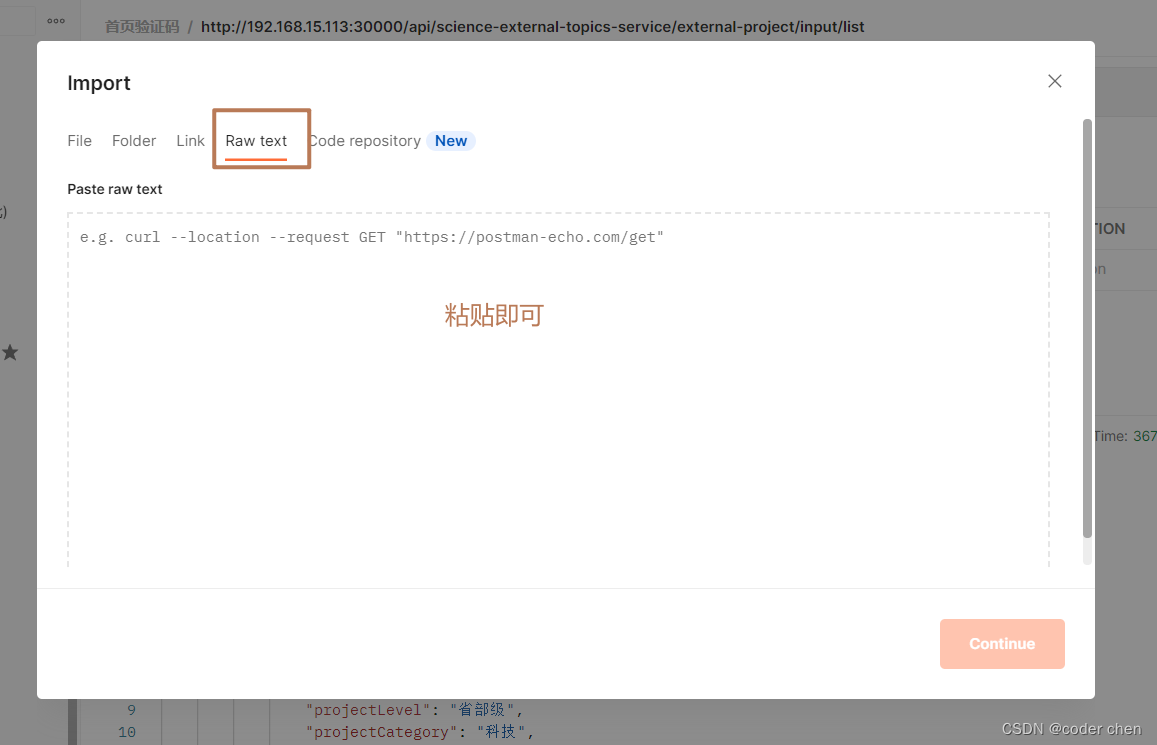
curl+postman 在java开发中的使用(提高效率)
概念 curl 是一个常用的命令行工具,用于发送各种类型的 HTTP 请求,包括 GET、POST、PUT、DELETE 等。它也可以用来下载文件、上传文件、设置 cookie、发送 multipart/form-data 等等。 使用 调用post接口 实际中的接口: curl --location…...
【电子取证:FTK IMAGER 篇】DD、E01系统镜像动态仿真
文章目录 【电子取证:FTK Imager 篇】DD、E01系统镜像动态仿真一、DD、E01系统镜像动态仿真 (一)使用到的软件 1、FTK Imager (v4.5.0.3)2、VMware Workstation 15 Pro (v15.5.2)(二)FTK Imager 挂载镜像 1、选择 …...

netcat瑞士军刀
netcat瑞士军刀 1、nc简介3、从示例中学习2、命令格式及常用参数 1、nc简介 nc(netcat)是一个短小精悍、功能实用、简单可靠的网络工具,主要有如下作用: (1)端口侦听,nc 可以作为 server 以 TC…...

【征稿倒计时十天】第三届高性能计算与通信工程国际学术会议(HPCCE 2023)
【有ISSN、ISBN号!!往届均已完成EI检索】 第三届高性能计算与通信工程国际学术会议(HPCCE 2023) 2023 3rd International Conference on High Performance Computing and Communication Engineering (HPCCE 2023) 2023年12月22-24日 | 中国哈尔滨 第三…...
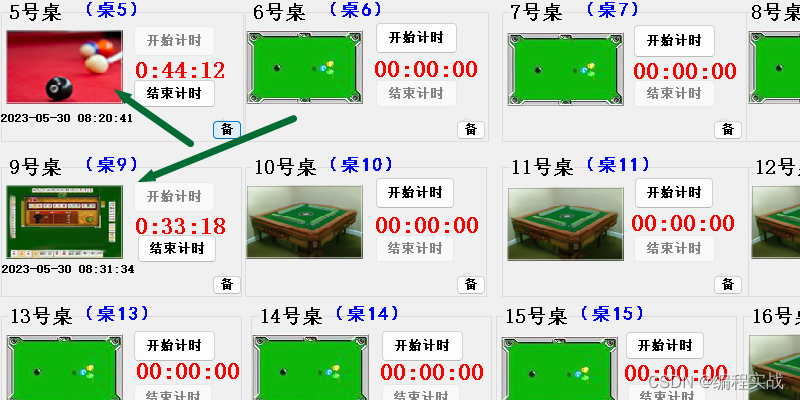
编程应用实际场景:台球厅怎么样用电脑给客人计时,台球计时收费系统操作教程
一、前言 准确控制顾客在店内游玩的时间,从而控制店内的各项成本,并提升店内的客流量。在顾客享受计时项目的时候,可以同时添加其他食物消费,并将单据合并统一结账。软件中的会员功能可以为客户办理会员可以使用灯控器控灯&#…...
云计算大屏,可视化云计算分析平台(云实时数据大屏PSD源文件)
大屏组件可以让UI设计师的工作更加便捷,使其更高效快速的完成设计任务。现分享可视化云分析系统、可视化云计算分析平台、云实时数据大屏的大屏Photoshop源文件,开箱即用! 若需 更多行业 相关的大屏,请移步小7的另一篇文章&#…...

高频js-----js执行机制 Event Loop
修改代码,让代码每隔1秒输出1-5 for (var i 0; i < 5;i) {setTimeout(() > {console.log(i)}, 1000)} 首先我们需要了解js的执行机制 (Event Loop) js是单线层,如果现在执行上面代码的话 会输出 5个5 这里不明白的同学可以去看一下我以前发布的关于EventLoop的文章 …...
恢复出厂设置后在 Android 上恢复照片的 6 种常用方法
恢复出厂设置可帮助您删除电子设备的所有信息并将其恢复到原始系统状态。但是,如果您不小心按下了恢复出厂设置按钮并从 Android 设备中删除了所有难忘的照片,该怎么办?好吧,您无需担心,因为可以通过以下一些方法来恢复…...

人工智能_机器学习065_SVM支持向量机KKT条件_深度理解KKT条件下的损失函数求解过程_公式详细推导_---人工智能工作笔记0105
之前我们已经说了KKT条件,其实就是用来解决 如何实现对,不等式条件下的,目标函数的求解问题,之前我们说的拉格朗日乘数法,是用来对 等式条件下的目标函数进行求解. KKT条件是这样做的,添加了一个阿尔法平方对吧,这个阿尔法平方肯定是大于0的,那么 可以结合下面的文章去看,也…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
