代码随想录算法训练营第37天|● 738.单调递增的数字 ● 968.监控二叉树 ● 总结
738. 单调递增的数字
中等
相关标签
相关企业
提示
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
示例 1:
输入: n = 10输出: 9
示例 2:
输入: n = 1234输出: 1234
示例 3:
输入: n = 332输出: 299
提示:
- 0 <= n <= 10(9)
思路
- 从后往前遍历
- 一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]–,然后strNum[i]给为9,这样这个整数就是89,即小于98的最大的单调递增整数。
代码
func monotoneIncreasingDigits(N int) int {s := strconv.Itoa(N)//将数字转为字符串,方便使用下标ss := []byte(s)//将字符串转为byte数组,方便更改。n := len(ss)if n <= 1 {return N}// 从后向前遍历332的数值变化为:332 -> 329 -> 299for i := n-1; i > 0; i-- {if ss[i-1] > ss[i] { //前一个大于后一位,前一位减1,后面的全部置为9ss[i-1] -= 1for j := i; j < n; j++ { //后面的全部置为9ss[j] = '9'}} }res, _ := strconv.Atoi(string(ss))return res
}
968. 监控二叉树
困难
相关标签
相关企业
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
[图片]
输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
[图片]
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是 [1, 1000]。
- 每个节点的值都是 0。
思路
- 局部最优:让叶子节点的父节点安摄像头
- 此时这道题目还有两个难点:
- 二叉树的遍历:后序遍历
- 如何隔两个节点放一个摄像头
- 如何隔两个节点放一个摄像头,来看看这个状态应该如何转移,先来看看每个节点可能有几种状态:有如下三种:
- 该节点无覆盖
- 本节点有摄像头
- 本节点有覆盖
相关文章:

代码随想录算法训练营第37天|● 738.单调递增的数字 ● 968.监控二叉树 ● 总结
738. 单调递增的数字 中等 相关标签 相关企业 提示 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 示例 1: 输入: n 10输出: …...

出现 java: 找不到符号 符号: 变量 log 的解决方法
目录 1. 问题所示2. 原理分析3. 解决方法3.1 增加编译参数3.2 增加lombok插件3.3 清楚本地缓存1. 问题所示 使用Springboot启动项目的时候,出现如下bug: java: 找不到符号符号: 变量 log位置: 类 org.springblade.example.consumer.rpc.BlogStu...
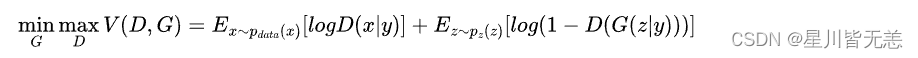
大数据机器学习与深度学习—— 生成对抗网络(GAN)
GAN概述 在讲GAN之前,先讲一个小趣事,你知道GAN是怎么被发明的吗?据Ian Goodfellow自己说: 之前他一直在研究生成模型,可能是一时兴起,有一天他在酒吧喝酒时,在酒吧里跟朋友讨论起生成模型。然…...

vue前端访问Django channels WebSocket失败
现象 前端报错:SSH.vue:51 WebSocket connection to ‘ws://127.0.0.1:8000/server/terminal/120.59.88.26/22/1/’ failed: 后端报错:Not Found: /server/terminal/120.79.83.26/22/1/ 原因 django的版本与channels的版本不匹配(django…...

厉害了!水浸监控技术有升级啦
水浸监控在今天的社会中变得愈发重要,特别是在各种行业和场所。面对突发的水灾,及时有效的监测和预警系统可以帮助组织减少损失,保障人员和财产的安全。 客户案例 商业办公楼 合肥某大型商业办公楼面临着水灾风险,而传统的监控系…...

【开题报告】基于SpringBoot的大学生心理教育平台的设计与实现
1.研究背景 大学生心理健康问题一直备受关注。随着社会压力的增加、人际关系的复杂化以及学业与就业压力等因素的影响,大学生心理健康问题日益突出。因此,设计并实现基于SpringBoot的大学生心理教育平台具有重要的研究意义和实践价值。 (1&…...
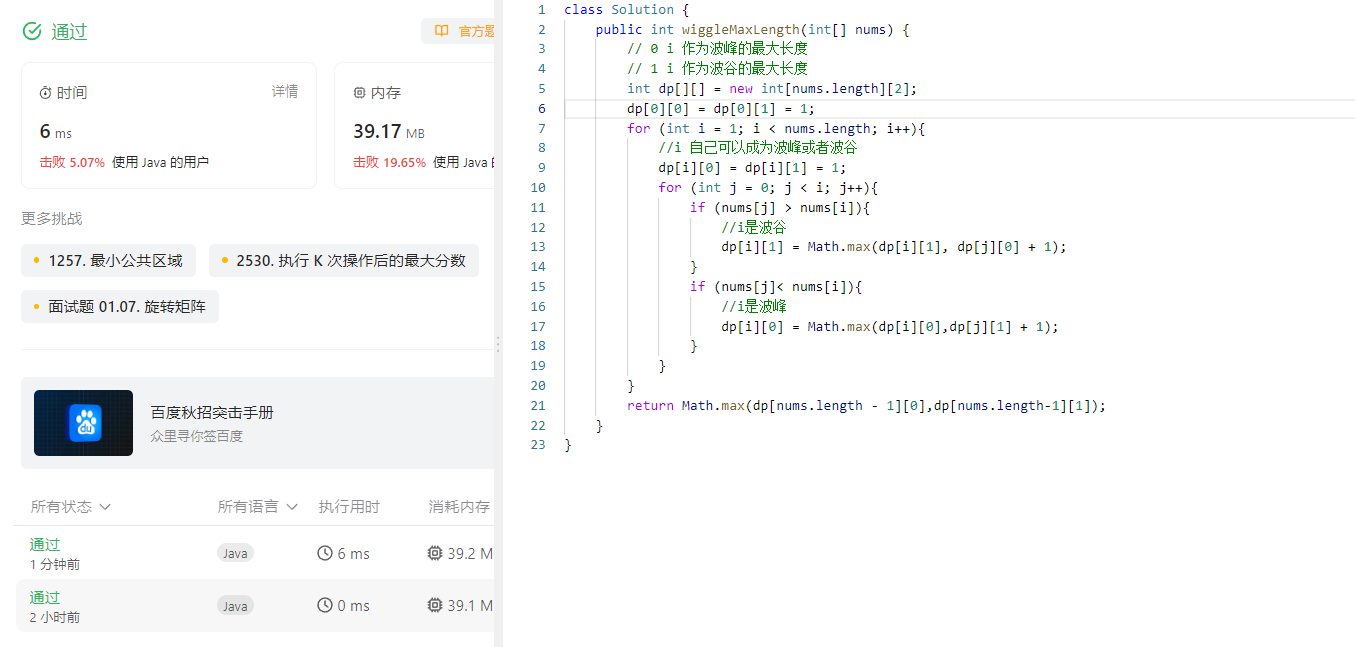
376. 摆动序列
376. 摆动序列 原题链接:完成情况:解题思路:参考代码:_376摆动序列_376摆动序列 错误经验吸取 原题链接: 376. 摆动序列 https://leetcode.cn/problems/wiggle-subsequence/description/ 完成情况: 解题…...

现在个人想上架微信小游戏已经这么难了吗...
引言 大家好,最近我突然想起来我还有一款微信小游戏还没有上架,于是捣鼓了一天把游戏完善了一下,然后准备提交审核,却发现异常的艰难... 1.为什么难? 相信大家都大概知道,自从微信平台宣布 9月1日起&…...
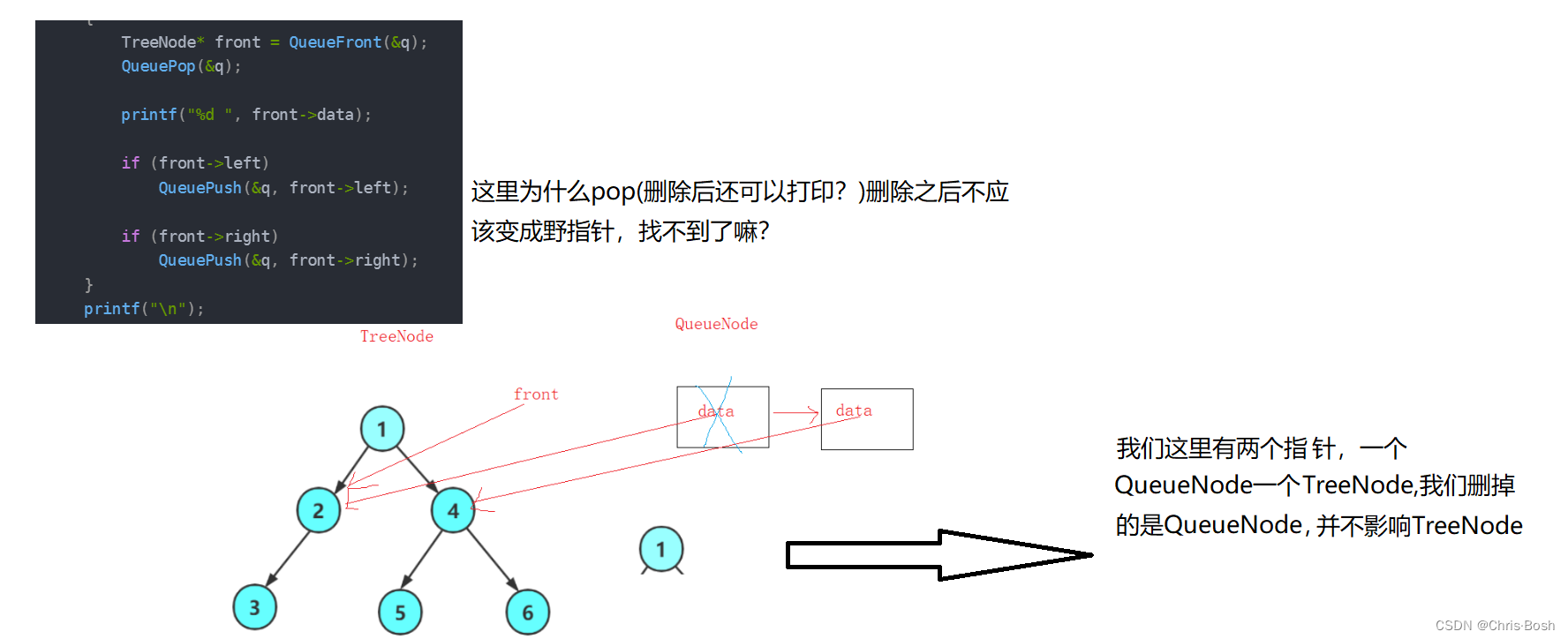
C语言数据结构-----二叉树(2)堆的深入理解及应用、链式二叉树的讲解及代码实现
前言 本篇文章讲述的内容有部分是上一节写过的。重复内容不会再进行说明,大家可以看上一节内容 链接: C语言数据结构-----二叉树(1)认识数、二叉树、堆及堆的代码实现 文章目录 前言1.使用堆解决TOP-K问题2.向下调整堆的时间复杂度与向上调整堆的时间复杂度对比3.堆…...

【算法】【动规】等差数列划分
跳转汇总链接 👉🔗算法题汇总链接 1.2 等差数列划分 🔗题目链接 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是…...
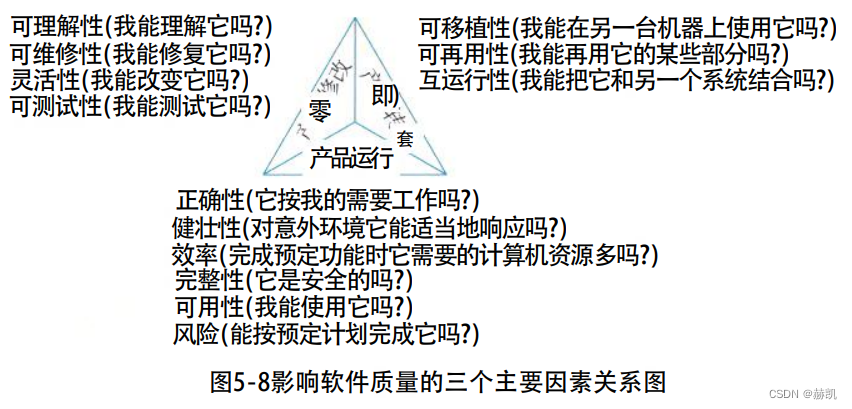
系统架构设计师教程(五)软件工程基础知识
软件工程基础知识 5.1 软件工程5.1.1 软件工程定义5.1.2 软件过程模型5.1.3 敏捷模型敏捷开发的特点敏捷方法的核心思想主要敏捷方法简介 5.1.4 统一过程模型 (RUP)RUP的生命周期RUP中的核心概念RUP的特点 5.1.5 软件能力成熟度模型 5.2 需求工程5.2.1 需求获取需求获取的基本步…...
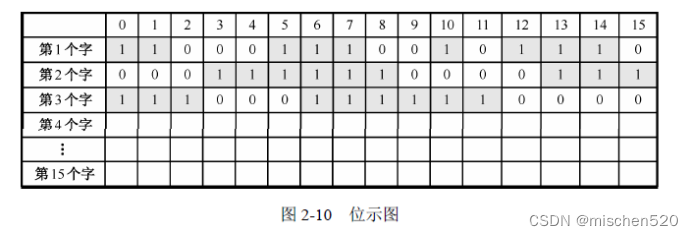
计算机中的文件管理
操作系统对计算机的管理包括两个方面:硬件资源和软件资源。硬件资源的管理包括CPU 的管理、存储器的管理、设备管理等,主要解决硬件资源的有效和合理利用问题。 软件资源包括各种系统程序、各种应用程序、各种用户程序,也包括大量的文档材料、…...

Linux常见排错思路及命令
Linux常见排错思路及命令 一、引言 在Linux系统中,由于其高度可配置和可定制的特性,可能会遇到各种问题。本文将介绍一些常见的排错思路,并提供一些常用的命令,以帮助您快速定位和解决问题。 二、常见排错思路 查看系统日志 …...

【springboot】【easyexcel】excel文件读取
目录 pom.xmlExcelVo逐行读取并处理全部读取并处理向ExcelListener 传参 pom.xml <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.1.1</version> </dependency>ExcelVo 字段映射…...
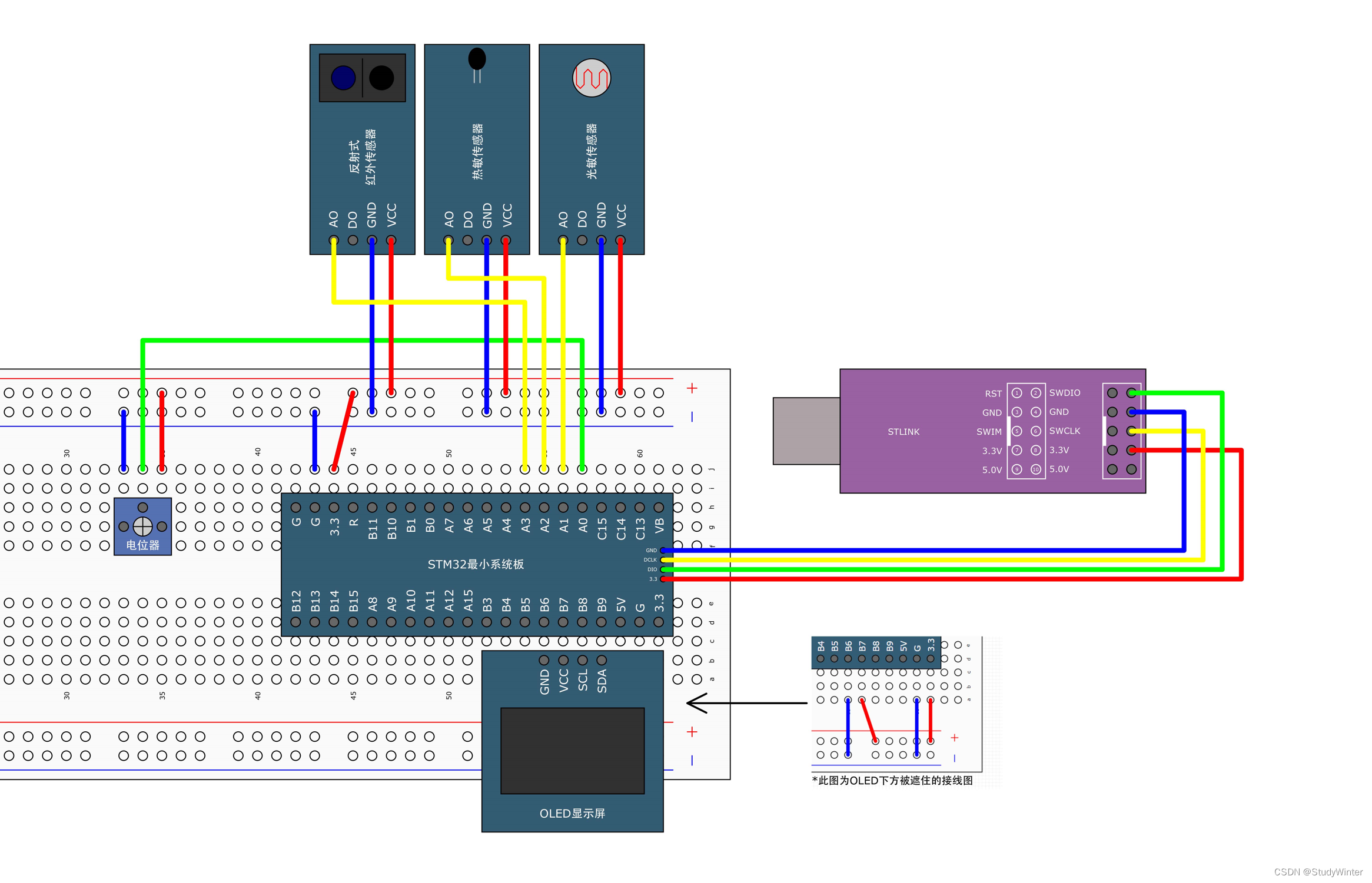
【STM32】ADC模数转换器
1 ADC简介 ADC(Analog-Digital Converter)模拟-数字转换器 ADC可以将引脚上连续变化的模拟电压转换为内存中存储的数字变量,建立模拟电路到数字电路的桥梁 STM32是数字电路,只有高低电平,没有几V电压的概念ÿ…...

Git篇---第九篇
系列文章目录 文章目录 系列文章目录前言一、使用过git merge和git rebase吗?它们之间有什么区别?二、使用过git cherry-pick,有什么作用?前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看…...

Paper Reading: (ACRST) 基于自适应类再平衡自训练的半监督目标检测
目录 简介工作重点方法CropBankFBRAFFRTwo-stage Pseudo-label Filtering 实验与SOTA比较消融实验 简介 题目:《Semi-Supervised Object Detection with Adaptive Class-Rebalancing Self-Training》,AAAI’22, 基于自适应类再平衡自训练的半…...

2023年贺岁电影:一眼多,二眼好多
如果从11月末开始统计,今年贺岁档共有72部贺岁片,平均一天就有2部电影上映,看完总计需要花费7400分钟。 这个数量几乎快赶上2021年到2022年贺岁片的总和。 今年电影市场快速回暖以来,多部爆款作品接力上映,持续刺激市…...

软件测试面试中基础与功能的问题
一、 你们的测试流程是怎么样的? 答:1.项目开始阶段, BA (需求分析师) 从用户方收集需求并将需求转化为规格说明书,接 下来在 项目组领导 会组织需求评审。 2.需求评审通过后,BA 会组织 项目…...

map|二分查找|离线查询|LeetCode:2736最大和查询
本文涉及的基础知识点 二分查找算法合集 题目 给你两个长度为 n 、下标从 0 开始的整数数组 nums1 和 nums2 ,另给你一个下标从 1 开始的二维数组 queries ,其中 queries[i] [xi, yi] 。 对于第 i 个查询,在所有满足 nums1[j] > xi 且…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
