MIT线性代数笔记-第28讲-正定矩阵,最小值
目录
- 28.正定矩阵,最小值
- 打赏
28.正定矩阵,最小值
由第 26 26 26讲的末尾可知在矩阵为实对称矩阵时,正定矩阵有以下四种判定方法(都是充要条件):
- 所有特征值都为正
- 左上角所有 k k k阶子矩阵行列式都为正( 1 ≤ k ≤ n 1 \le k \le n 1≤k≤n)
- 所有主元都为正
- 对于任意非零实向量 x ⃗ \vec{x} x均满足 x ⃗ T M x ⃗ > 0 \vec{x}^T M \vec{x} > 0 xTMx>0
其中最后一种常常作为正定矩阵的定义
当上述判定条件中的正都换为非负时,得到的就是半正定矩阵
对于一个实对称矩阵 A A A, x ⃗ T A x ⃗ \vec{x}^T A \vec{x} xTAx等于一个由二次项构成的多项式,这种形式就是矩阵的二次型
例: 对于矩阵 A = [ 2 6 6 7 ] A = \begin{bmatrix} 2 & 6 \\ 6 & 7 \end{bmatrix} A=[2667],它的二次型为 x ⃗ T A x ⃗ = [ x 1 x 2 ] [ 2 6 6 7 ] [ x 1 x 2 ] = 2 x 1 2 + 12 x 1 x 2 + 7 x 2 2 \vec{x}^T A \vec{x} = \begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} 2 & 6 \\ 6 & 7 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = 2 x_1^2 + 12 x_1 x_2 + 7 x_2^2 xTAx=[x1x2][2667][x1x2]=2x12+12x1x2+7x22
-
容易证明无论对于多少阶的实对称矩阵,得到的都是二次项构成的多项式,即不存在三次型,四次型等
也就是说如果一个实对称矩阵的二次型恒大于零,那么它是一个正定矩阵,当考虑一个多元二次函数是否恒为正时,可以找到对应的对称矩阵并判断是否为正定矩阵
如果这个多元二次函数有二次项或常数项,可以给 x ⃗ \vec{x} x末尾添加一个元素 1 1 1,那么对应的对称矩阵最后一个元素即为常数项的值,最后一列和最后一行的元素(除最后一个)依次为对应的自变量的系数的二分之一
即函数 f ( x 1 , ⋯ , x n ) = a 1 , 1 x 1 2 + ⋯ + a n , n x n 2 + b 1 x 1 + ⋯ + b n x n + c f(x_1 , \cdots , x_n) = a_{1 , 1} x_1^2 + \cdots + a_{n , n} x_n^2 + b_1 x_1 + \cdots + b_n x_n + c f(x1,⋯,xn)=a1,1x12+⋯+an,nxn2+b1x1+⋯+bnxn+c(其中 a i , j a_{i , j} ai,j表示 x i x j x_i x_j xixj的系数)对应的对称矩阵为
[ a 1 , 1 a 1 , 2 2 ⋯ b 1 2 a 1 , 2 2 a 2 , 2 ⋯ b 2 2 ⋮ ⋮ ⋱ ⋮ b 1 2 b 2 2 ⋯ c ] \begin{bmatrix} a_{1 , 1} & \dfrac{a_{1 , 2}}{2} & \cdots & \dfrac{b_1}{2} \\ \dfrac{a_{1 , 2}}{2} & a_{2 , 2} & \cdots & \dfrac{b_2}{2} \\ \vdots & \vdots & \ddots & \vdots \\ \dfrac{b_1}{2} & \dfrac{b_2}{2} & \cdots & c \end{bmatrix} a1,12a1,2⋮2b12a1,2a2,2⋮2b2⋯⋯⋱⋯2b12b2⋮c ,不过此时“对应的对称矩阵是正定矩阵”就成了充分条件而非充要条件
-
考虑将一个二阶实对称矩阵的二次型表示为图像,继续使用刚才的例子 [ 2 6 6 7 ] \begin{bmatrix} 2 & 6 \\ 6 & 7 \end{bmatrix} [2667]得到 z = 2 x 2 + 12 x y + 7 y 2 z = 2x^2 + 12xy + 7y^2 z=2x2+12xy+7y2
- 当 y = 0 , x = 0 y = 0 , x = 0 y=0,x=0时,分别得到 z O x zOx zOx面和 y O z yOz yOz面上的二次函数
- 当 x = y x = y x=y时,得到一个 z O x zOx zOx面和 y O z yOz yOz面中间的二次函数
依此类推可以发现在部分情况下 z < 0 z < 0 z<0,并且可以想象到这个函数图像类似一个马鞍,原点是一个鞍点,在某个方向是极大值,在另一个方向是极小值
反之,当矩阵为正定矩阵时,图像类似一个碗(抛物面)
此时将图像水平切开,即令 z z z为一个常数,那么马鞍图像的截面为一个双曲线,碗图像的截面为一个椭圆
-
把刚才的例子的最后一个元素换为 20 20 20,得到 [ 2 6 6 20 ] \begin{bmatrix} 2 & 6 \\ 6 & 20 \end{bmatrix} [26620]
二者的二次型分别配方得到 { 2 x 1 2 + 12 x 1 x 2 + 7 x 2 2 = 2 ( x + 3 y ) 2 − 11 y 2 2 x 1 2 + 12 x 1 x 2 + 20 x 2 2 = 2 ( x + 3 y ) 2 + 2 y 2 \left \{ \begin{matrix} 2 x_1^2 + 12 x_1 x_2 + 7 x_2^2 = 2(x + 3y)^2 - 11y^2 \\ 2 x_1^2 + 12 x_1 x_2 + 20 x_2^2 = 2(x + 3y)^2 + 2y^2 \end{matrix} \right. {2x12+12x1x2+7x22=2(x+3y)2−11y22x12+12x1x2+20x22=2(x+3y)2+2y2
实际上配方后这些平方的系数和实对称矩阵的主元有关
例如 [ 2 6 6 20 ] L U \begin{bmatrix} 2 & 6 \\ 6 & 20 \end{bmatrix} LU [26620]LU分解后得到 [ 1 0 3 1 ] [ 2 6 0 2 ] L U \begin{matrix} \begin{bmatrix} 1 & 0 \\ 3 & 1 \end{bmatrix} & \begin{bmatrix} 2 & 6 \\ 0 & 2 \end{bmatrix} \\ L & U \end{matrix} [1301]L[2062]U,两个主元分别用作平方的系数,而 3 3 3用作第一个平方里 y y y的系数
n n n阶实对称矩阵的二次型可以写成 d 1 ( x 1 + ⋯ + e 1 , n x n ) 2 + d 2 ( x 2 + ⋯ + e 2 , n x n ) 2 + ⋯ + d n x n 2 d_1(x_1 + \cdots + e_{1 , n} x_n)^2 + d_2(x_2 + \cdots + e_{2 , n} x_n)^2 + \cdots + d_n x_n^2 d1(x1+⋯+e1,nxn)2+d2(x2+⋯+e2,nxn)2+⋯+dnxn2
模拟一下消元过程可以发现 d i = u i , i , e i , j = l j , i d_i = u_{i , i} , e_{i , j} = l_{j , i} di=ui,i,ei,j=lj,i( u , l u , l u,l表示 L U LU LU分解后 U , L U , L U,L中的元素),这是可以证明的,但是我还没找到描述起来比较简洁的证明方法
由此可以发现平方项的系数即为对应主元,所以正定矩阵的主元均为正数
-
已知某个二元函数 f ( x , y ) f(x , y) f(x,y)在 ( x 0 y 0 ) (x_0 y_0) (x0y0)处有极小值的一个充分条件是函数在 ( x 0 , y 0 ) (x_0 , y_0) (x0,y0)的某邻域内连续且有一阶及二阶偏导数,又 f x ( x 0 , y 0 ) = f x ( x 0 , y 0 ) = 0 , f x x ( x 0 , y 0 ) f y y ( x 0 , y 0 ) − f x y 2 ( x 0 , y 0 ) > 0 f_x(x_0 , y_0) = f_x(x_0 , y_0) = 0 , f_{xx}(x_0 , y_0) f_{yy}(x_0 , y_0) - f_{xy}^2(x_0 , y_0) > 0 fx(x0,y0)=fx(x0,y0)=0,fxx(x0,y0)fyy(x0,y0)−fxy2(x0,y0)>0且 f x x ( x 0 , y 0 ) > 0 f_{xx}(x_0 , y_0) > 0 fxx(x0,y0)>0
易证最后两个条件刚好与矩阵 [ f x x ( x 0 , y 0 ) f x y ( x 0 , y 0 ) f y x ( x 0 , y 0 ) f y y ( x 0 , y 0 ) ] \begin{bmatrix} f_{xx}(x_0 , y_0) & f_{xy}(x_0 , y_0) \\ f_{yx}(x_0 , y_0) & f_{yy}(x_0 , y_0) \end{bmatrix} [fxx(x0,y0)fyx(x0,y0)fxy(x0,y0)fyy(x0,y0)]是正定矩阵等价
这还可以推广至更加多元的函数
证明: 暂时不会证明 \color{OrangeRed}暂时不会证明 暂时不会证明
-
对于一个二阶正定矩阵 A A A,把它拆为 Q Λ Q T Q \Lambda Q^T QΛQT,其中的 Q , Q T Q , Q^T Q,QT可以分别被视为行向量和列向量的旋转矩阵,并且二者导致的旋转一样
令 x ⃗ T A x ⃗ = x ⃗ T Q Λ Q T x ⃗ = 1 \vec{x}^T A \vec{x} = \vec{x}^T Q \Lambda Q^T \vec{x} = 1 xTAx=xTQΛQTx=1,依本讲第 2 2 2点可知这是一个中心在原点正上方的平行于 x O y xOy xOy面的斜椭圆的方程,容易发现两个特征值分别决定斜椭圆长轴和短轴长度,即 2 1 λ 1 , 2 1 λ 2 2 \sqrt{\dfrac{1}{\lambda_1}} , 2 \sqrt{\dfrac{1}{\lambda_2}} 2λ11,2λ21分别为长轴和短轴长度(其中 λ 1 < λ 2 \lambda_1 < \lambda_2 λ1<λ2),两个特征向量分别与长轴和短轴方向一致
推广到更加高阶,这种关系也是成立的,比如三阶正定矩阵的三个特征值倒数的平方根的两倍分别等于对应椭球的三个主轴长度,三个特征向量分别与三个主轴方向一致
这就是为什么这种拆分被称为主轴定理
证明: 暂时不会证明 \color{OrangeRed}暂时不会证明 暂时不会证明
打赏
制作不易,若有帮助,欢迎打赏!


相关文章:

MIT线性代数笔记-第28讲-正定矩阵,最小值
目录 28.正定矩阵,最小值打赏 28.正定矩阵,最小值 由第 26 26 26讲的末尾可知在矩阵为实对称矩阵时,正定矩阵有以下四种判定方法(都是充要条件): 所有特征值都为正左上角所有 k k k阶子矩阵行列式都为正&…...
Python:五种算法RFO、GWO、DBO、HHO、SSA求解23个测试函数
一、五种算法介绍 (1)红狐优化算法(Red fox optimization,RFO) (2)灰狼优化算法(Grey Wolf Optimizer,GWO) (3)蜣螂优化算法(Dung beetle opti…...

如何参与开源项目
大家好,受卡哥邀请,和大家分享一下开源活动的相关经验。首先简要自我介绍一下,我目前在一所985研二在读,主要学习大数据方向,从去年开始参与开源活动近一年时间,也对多个Apache框架有所贡献。 由于学校或专…...
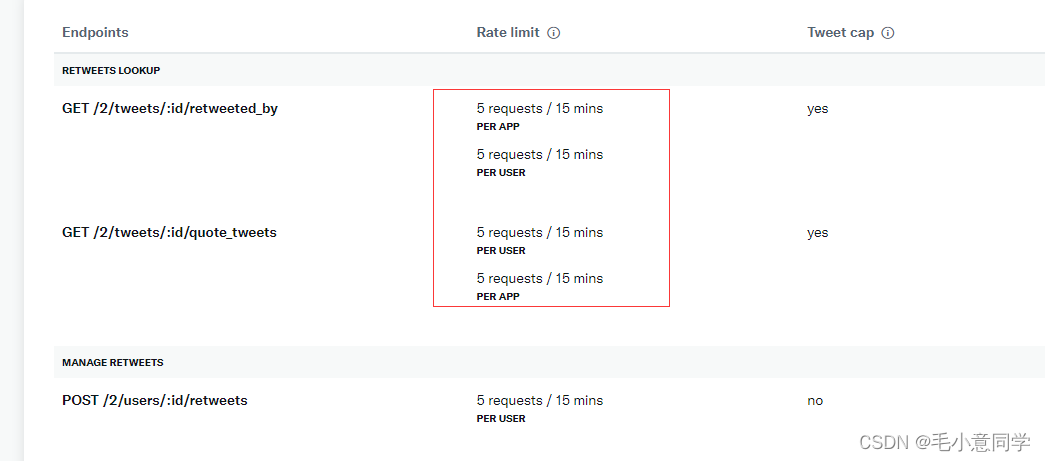
twitter开发如何避坑
此篇介绍在twitter开发过程中遇到的坑(尤其是费用的坑)。 一坑:免费接口少! 刚开始申请免费API使用的时候,twitter官方只会给你三个免费接口使用。 发twitter、删推文、查看用户信息。 这三个接口远远不够开发中使用…...
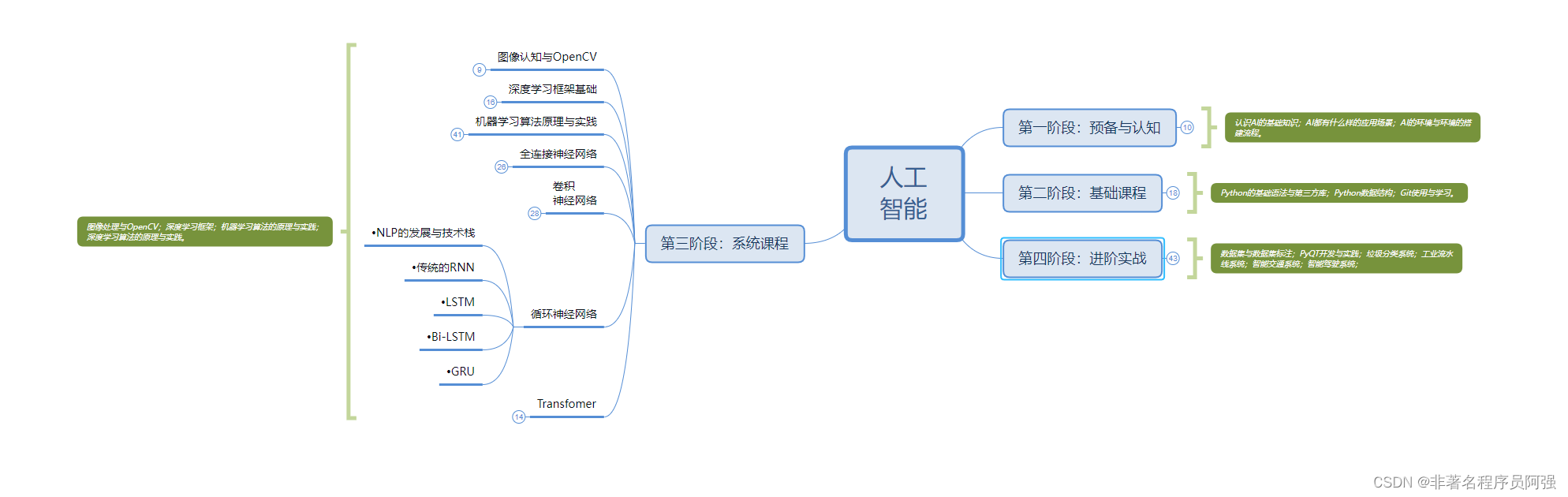
人工智能算法合集
人工智能(Artificial Intelligence,AI)作为当今世界最热门的技术领域之一,正日益改变着我们的生活方式、工作方式甚至整个社会结构。在人工智能领域中,算法是至关重要的一环,它们是实现人工智能技术应用的核…...

PythonStudio:一款国人写的python及窗口开发编辑IDE,可以替代pyqt designer等设计器了
本款软件只有十几兆,功能算是强大的,国人写的,很不错的python界面IDE.顶部有下载链接。下面有网盘下载链接,或者从官网直接下载。 目前产品免费,以后估计会有收费版本。主页链接:PythonStudio-硅量实验室 作…...
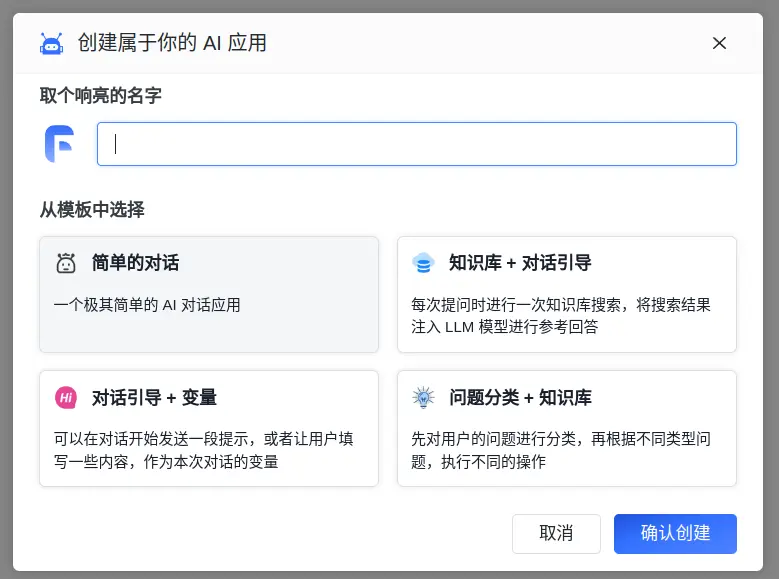
大模型应用_FastGPT
1 功能 整体功能,想解决什么问题 官方说明:FastGPT 是一个基于 LLM 大语言模型的知识库问答系统,提供开箱即用的数据处理、模型调用等能力。同时可以通过 Flow 可视化进行工作流编排,从而实现复杂的问答场景!个人体会…...

elasticsearch|大数据|elasticsearch的api部分实战操作以及用户和密码的管理
一, 前言 本文主要内容是通过elasticsearch的api来进行一些集群的管理和信息查询工作,以及elasticsearch用户的增删改查和密码的重设以及重置如何操作 接上文:elasticsearch|大数据|elasticsearch低版本集群的部署安装和安全增强---密码设…...

Android多进程和跨进程通讯方式
前言 我们经常开发过程中经常会听到线程和进程,在讲述Android进程多进程前我打算先简单梳理一下这俩者。 了解什么是进程与线程 进程: 系统中正在运行的一个应用程序,某个程序一旦运行就是一个进程,是资源分配的最小单位&#…...

通过Jenkins将应用发布到K8s1.24.3
一、准备基础环境 cat >> /etc/hosts <<EOF 192.168.180.210 k8s-master 192.168.180.200 k8s-node1 192.168.180.190 k8s-node2 192.168.180.180 gitlab 192.168.180.170 jenkins 192.168.180.160 harbor EOF 配置主机名 hostnamectl set-hostname k8s-master &am…...

正则表达式入门与实践
文章目录 一、为什么要有正则二、正则表达式基础概念三、Pattern与Matcher类的使用(一)Pattern类的常用方法(二)Matcher类的常用方法四、常用正则规则及其含义(一)规范表示(二)数量表示(三)逻辑运算符五、String对正则表达式的支持六、实践演练(一)匹配给定文本中的…...
C++初阶(十六)优先级队列
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、priority_queue的介绍和使用1、priority_queue的介绍2、priority_queue的使用 二、priori…...
深入探索C语言中的二叉树:数据结构之旅
引言 在计算机科学领域,数据结构是基础中的基础。在众多数据结构中,二叉树因其在各种操作中的高效性而脱颖而出。二叉树是一种特殊的树形结构,每个节点最多有两个子节点:左子节点和右子节点。这种结构使得搜索、插入、删除等操作…...

如何发现服务器被入侵了,服务器被入侵了该如何处理?
作为现代社会的重要基础设施之一,服务器的安全性备受关注。服务器被侵入可能导致严重的数据泄露、系统瘫痪等问题,因此及时排查服务器是否被侵入,成为了保障信息安全的重要环节。小德将给大家介绍服务器是否被侵入的排查方案,并采…...
CSDN一键注释功能
这是什么牛逼哄哄的功能 看这里: 然后: 再试一个: 输出结果是?package yuyi03.interview;/*** ClassName: InterviewTest2* Package: yuyi03.interview* Description:** Author 雨翼轻尘* Create 2023/12/14 0014 0:08*/ publ…...
基于JAVA的校园电子商城系统论文
摘 要 网络技术和计算机技术发展至今,已经拥有了深厚的理论基础,并在现实中进行了充分运用,尤其是基于计算机运行的软件更是受到各界的关注。加上现在人们已经步入信息时代,所以对于信息的宣传和管理就很关键。因此校园购物信息的…...
直播传媒公司网站搭建作用如何
直播已然成为抖快等平台的主要生态之一,近些年主播也成为了一种新行业,相关的mcn机构直播传播公司等也时有开业,以旗下主播带来高盈利,而在实际运作中也有一些痛点难题: 1、机构宣传展示难 不少散主播往往会选择合作…...

数据结构与算法-动态规划-机器人达到指定位置方法数
机器人达到指定位置方法数 来自左程云老师书中的一道题 【题目】 假设有排成一行的 N 个位置,记为 1~N,N 一定大于或等于 2。开始时机器人在其中的 M 位置上(M 一定是 1~N 中的一个),机器人可以往左走或…...
-docker的基本使用)
K8S学习指南(2)-docker的基本使用
文章目录 引言安装 DockerDocker 基本概念1. 镜像(Images)示例:拉取并运行一个 Nginx 镜像 2. 容器(Containers)示例:查看运行中的容器 3. 仓库(Repository)示例:推送镜像…...

java 执行linux 命令
文章目录 前言一、linux命令执行二、使用步骤三、踩坑 前言 java 执行linux 命令; 本文模拟复制linux文件到指定文件夹后打zip包后返回zip名称,提供给下载接口下载zip; 一、linux命令执行 linux命令执行Process process Runtime.getRunti…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
