深入探索C语言中的二叉树:数据结构之旅
引言
在计算机科学领域,数据结构是基础中的基础。在众多数据结构中,二叉树因其在各种操作中的高效性而脱颖而出。二叉树是一种特殊的树形结构,每个节点最多有两个子节点:左子节点和右子节点。这种结构使得搜索、插入、删除等操作可以在对数时间复杂度内完成,这对于算法性能的提升至关重要。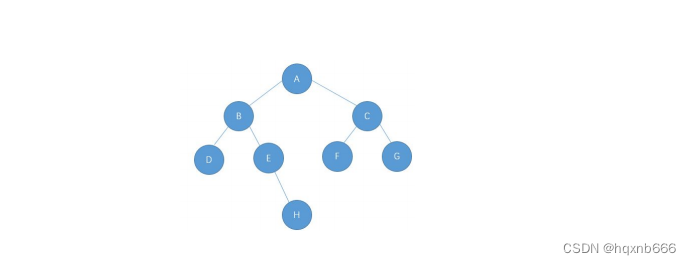
核心内容
-
二叉树的基本概念
-
我们首先需要理解什么是二叉树。在本文的代码中,二叉树由结构体
BinaryTreeNode表示,每个节点包含数据以及指向左右子节点的指针。 -
创建和销毁二叉树
代码演示了如何使用
BuyTreeNode函数为一个新节点分配内存,并通过CreateNode函数来构建一个简单的二叉树。同时,DestoryTree函数展示了如何安全地销毁二叉树,释放其占用的资源。 -
二叉树的遍历
遍历是二叉树中最重要的操作之一。我们介绍了三种基本的遍历方式:前序(
PrevOrder)、中序(InOrder)和后序(PostOrder)遍历。这些遍历方法在二叉树的搜索和排序操作中发挥着关键作用。 -
二叉树的其他属性
除了遍历,我们还探讨了如何使用代码来确定二叉树的大小(
TreeSize)、叶子节点的数量(TreeLeafSize)、树的高度(TreeHeight)以及特定层级的节点数(TreeLeveLK)。 -
层序遍历的实现
除了深度优先遍历,层序遍历(
LevelOrder)也是一种重要的遍历方式。它按照节点所在的层级依次访问,这在某些特定的应用场景下非常有用,例如在构建搜索算法或执行宽度优先搜索时。
代码目录
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <math.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}TreeNode;TreeNode* BuyTreeNode(int x);
TreeNode* CreateNode();
void PrevOrder(TreeNode* root);//前序遍历 --深度优先遍历 dfs
void InOrder(TreeNode* root);
void PostOrder(TreeNode* root);
int TreeSize(TreeNode* root);
int TreeLeafSize(TreeNode* root);//叶子节点个数
int TreeHeight(TreeNode* root);//高度
int TreeLeveLK(TreeNode* root, int k);//第k层节点个数
TreeNode* TreeCreate(char* a, int* pi);//构建二叉树
void DestoryTree(TreeNode** root);//销毁二叉树
void LevelOrder(TreeNode* root);//层序遍历 --广度优先遍历bfs1.二叉树的基本概念和结构
在深入了解二叉树之前,我们必须首先理解它的基本构成。二叉树是一种非常重要的数据结构,广泛应用于编程和算法设计中。它是一个有序树,每个节点最多有两个子节点,通常被称为左子节点和右子节点。
结构体表示二叉树
在我的代码中,二叉树通过结构体BinaryTreeNode表示。这个结构体定义了树的基本单元——节点。每个节点包含三个部分:数据部分和两个指针。
typedef struct BinaryTreeNode {BTDataType data; // 节点存储的数据struct BinaryTreeNode* left; // 指向左子节点的指针struct BinaryTreeNode* right; // 指向右子节点的指针
} TreeNode;
这种结构体的设计允许二叉树以递归的方式定义:每个节点本身可以被视为一个树的根,具有自己的子树。二叉树的这种特性是其许多算法操作的基础,包括遍历、搜索和修改。
数据与节点关系
在这个结构体中,data字段存储了节点的值。这个值可以是任意类型,在我的示例中,它被定义为BTDataType(在这里是int类型)。每个节点的left和right指针分别指向它的左子节点和右子节点。如果某个节点不存在左子节点或右子节点,相应的指针将为NULL。
这种结构使得操作和遍历二叉树变得可能,允许我们实现诸如插入、删除、查找等复杂操作,同时也为高效的算法实现提供了基础。
在后续部分,我们将探索如何使用这种结构体来创建和管理二叉树
2.创建和销毁二叉树
在操作二叉树时,正确地管理内存是至关重要的。这涉及到两个基本操作:创建二叉树和销毁二叉树。在您的代码中,这两个过程通过BuyTreeNode、CreateNode和DestoryTree函数实现。
创建二叉树
-
分配节点内存:
BuyTreeNode函数用于创建一个新的树节点。它接受一个数据值,分配足够的内存来存储一个新的TreeNode结构体,并将传入的数据值赋给新节点
TreeNode* BuyTreeNode(int x) {TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));assert(node); // 确保内存分配成功node->data = x;node->left = NULL;node->right = NULL;return node;
}
构建二叉树(1):
TreeNode* TreeCreate(char* a, int* pi)
{if (a[*pi] == '#')return NULL;TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));if (root == NULL){perror("malloc fail");exit(-1);}root->data = a[(*pi)++];root->left = TreeCreate(a, pi);root->right = TreeCreate(a, pi);return root;
}过程步骤
-
检查终止条件: 函数首先检查当前位置的字符是否为
'#'。在这个上下文中,'#'代表一个空位置,意味着在这里不需要创建节点。如果是'#',函数返回NULL,这表明当前没有节点被创建,相当于告诉递归调用的上一层,这里是一个空分支。 -
创建新节点: 如果当前位置的字符不是
'#',函数会继续创建一个新的树节点。它分配内存空间给新节点,并检查内存分配是否成功。如果分配失败,函数会报错并退出程序。 -
设置节点数据: 新节点的数据设置为当前字符数组位置的值。然后,指针
pi递增,以便下一次调用时读取下一个字符。 -
递归构建子树: 接下来,函数递归地调用自身两次:一次用于构建左子树,一次用于构建右子树。这两个递归调用分别处理字符数组中接下来的部分,因此逐渐构建出整个树的结构。
-
返回树的根节点: 一旦左右子树都被创建,函数返回当前创建的节点,这个节点现在是一个完整子树的根节点。
说明
通过这种方式,TreeCreate函数能够从一个序列化的表示(在这里是一个字符数组)中逐步重建出原始的二叉树结构。这种序列化表示通常包含特殊的字符(如'#')来标示空节点,从而允许树的形状在数组中得以完整表达。
这个函数的递归性质使得它能够处理任意复杂的树结构,只要输入的字符数组正确地表示了树的结构。这种方法在二叉树的序列化和反序列化中非常常见,是处理树结构数据的一种强大技巧。
构建二叉树(2): CreateNode函数展示了如何将这些独立的节点组合成一个完整的二叉树结构。这个函数硬编码了节点的创建和连接方式,构造了一个特定的二叉树。
TreeNode* CreateNode() {TreeNode* node1 = BuyTreeNode(1);TreeNode* node2 = BuyTreeNode(2);...node1->left = node2;node1->right = node4;...return node1;
}
销毁二叉树
内存管理的另一方面是当二叉树不再需要时,正确地释放其占用的资源。这是通过DestoryTree函数实现的。
-
递归销毁:
DestoryTree采用递归方式访问每个节点,并释放其占用的内存。递归是处理树结构的一种自然和强大的方法。
void DestoryTree(TreeNode** root) {if (*root == NULL)return;DestoryTree(&(*root)->left);DestoryTree(&(*root)->right);free(*root);*root = NULL;
}
这种方法确保了所有节点都被适当地访问和释放,从而防止了内存泄漏——一种在长时间运行的程序中特别重要的考虑因素。
通过这些函数的实现,我们不仅构建了一个基本的二叉树,还学会了如何负责任地管理与之相关的内存。下一步,我们将探讨如何遍历二叉树,并了解它的其他重要属性
3.二叉树的其他属性
除了遍历,我们还探讨了如何使用代码来确定二叉树的大小(TreeSize)、叶子节点的数量(TreeLeafSize)、树的高度(TreeHeight)以及特定层级的节点数(TreeLeveLK)在理解了二叉树的基本结构和如何创建及销毁它之后,我们接下来会探索二叉树的几个其他重要属性:树的大小、叶子节点的数量、树的高度,以及特定层级的节点数。这些属性在二叉树的应用和分析中扮演着关键角色。
1. 二叉树的大小(TreeSize)
二叉树的大小是指树中节点的总数。这可以通过递归地计算每个节点的左右子树来确定。
int TreeSize(TreeNode* root) {if (root == NULL) {return 0;}return 1 + TreeSize(root->left) + TreeSize(root->right);
}
在这个函数中,如果当前节点为NULL,表示子树不存在,因此返回0。否则,计算大小时,将当前节点(1)加上左子树和右子树的大小。
2. 叶子节点的数量(TreeLeafSize)
叶子节点是指没有子节点的节点。计算二叉树中叶子节点的数量有助于理解树的分布和深度。
int TreeLeafSize(TreeNode* root) {if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL) {return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
当遇到叶子节点时(即左右子节点均为NULL),返回1。否则,递归地计算左右子树中的叶子节点数量。
3. 树的高度(TreeHeight)
树的高度是从根到最远叶子节点的最长路径上的节点数。这是衡量树平衡和深度的重要指标。
int TreeHeight(TreeNode* root) {if (root == NULL) {return 0;}return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}
在这个函数中,如果节点为NULL,表示到达了树的底部,返回0。否则,高度是左右子树高度的最大值加1(当前节点)。
4. 特定层级的节点数(TreeLeveLK)
计算特定层级的节点数有助于理解树在不同深度的分布。
int TreeLeveLK(TreeNode* root, int k) {if (root == NULL || k < 1) {return 0;}if (k == 1) {return 1;}return TreeLeveLK(root->left, k - 1) + TreeLeveLK(root->right, k - 1);
}
当到达目标层级(k == 1)时,返回1。如果不是目标层级,递归地计算左右子树在k-1层级的节点数。
通过这些函数,我们不仅能够构建和管理二叉树,还能深入了解树的结构和特性。这些属性对于优化算法、分析数据结构性能等方面都至关重要。接下来,我们将研究二叉树的遍历方法,这是理解和操作二叉树的关键一环。
1.二叉树的遍历
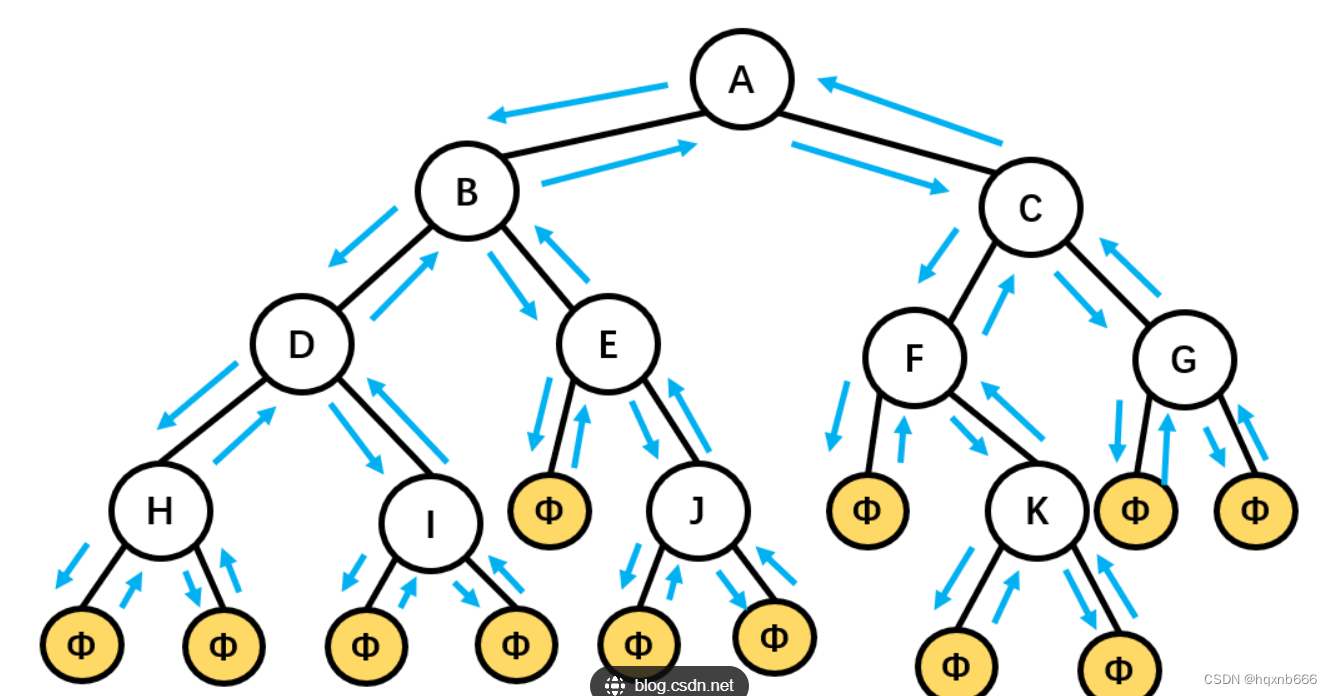
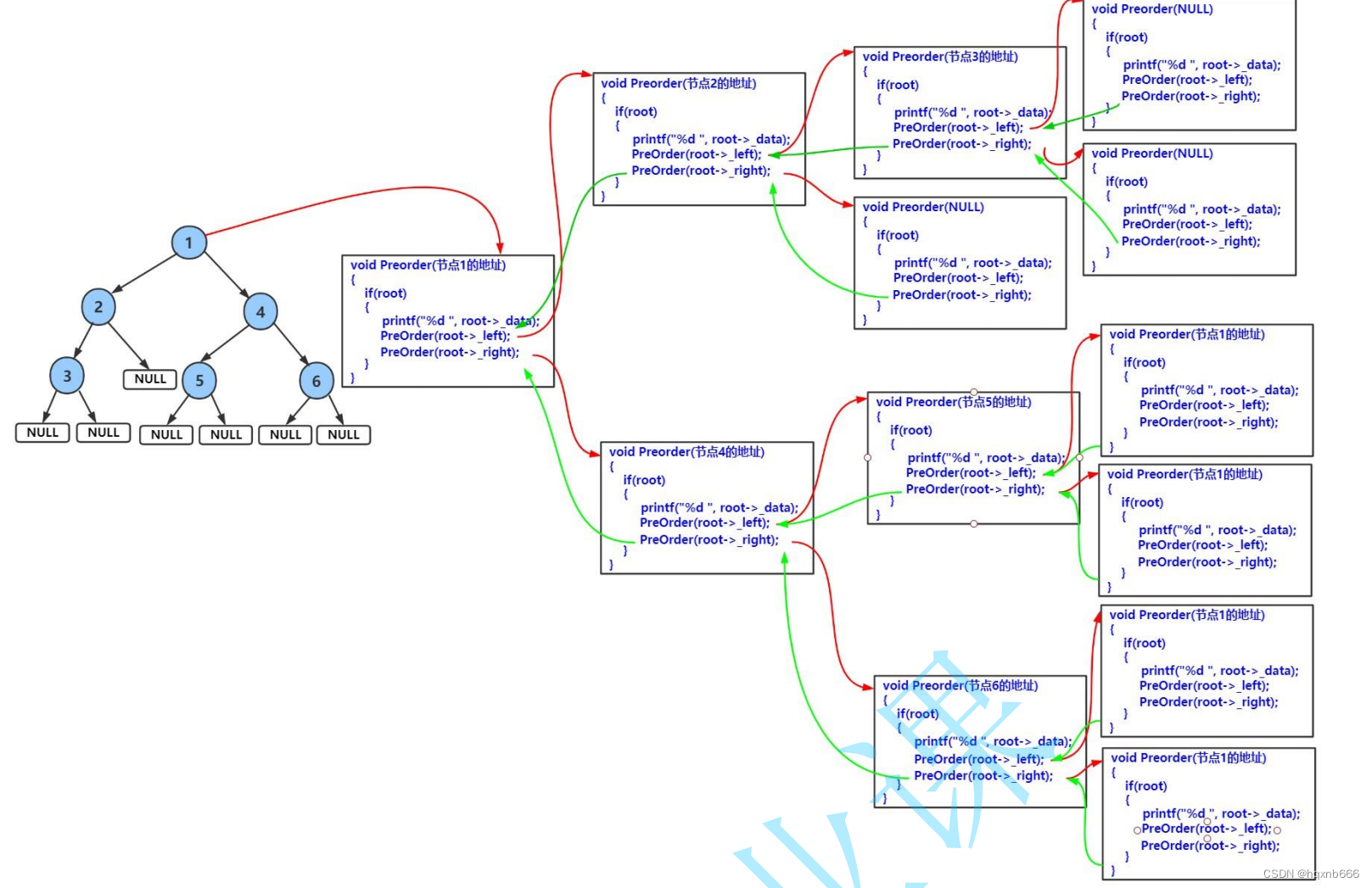
void PrevOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
void InOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
void PostOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}2. 层序遍历
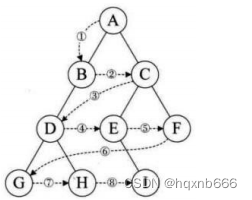
层序遍历 --广度优先遍历bfs 比如扫雷和基本搜索算法中就是以广度优先算法为基底
void LevelOrder(TreeNode* root)
{Queue q; QueueInit(&q);if (root)QueuePush(&q, root);int LevelSize = 1;while (!QueueEmpty(&q)){while (LevelSize--)//这里稍作变形,很多面试常考 控制层序遍历每一层每一层的输出{TreeNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");LevelSize = QueueSize(&q);}printf("\n");QueueDestory(&q);
}层序遍历是一种特殊的遍历方式,它按照树的层级,从上到下、从左到右的顺序访问每个节点。在我的函数中,这是通过使用一个队列实现的,队列是一种先进先出(FIFO)的数据结构。
过程步骤
-
初始化队列: 首先,创建一个空队列,用于存储将要访问的树节点。
-
根节点入队: 如果二叉树不为空,把根节点放入队列。这是遍历的起始点。
-
遍历队列中的节点: 接下来的步骤是循环进行的,直到队列为空。在每一次循环中,执行以下操作:
-
处理当前层级的节点: 对于队列中的每个节点,执行以下子步骤:
- 从队列中取出一个节点。
- 访问该节点(比如,打印节点数据)。
- 如果这个节点有左子节点,将左子节点加入队列。
- 如果这个节点有右子节点,将右子节点加入队列。
-
这个过程将会持续,直到队列为空。每处理完一层的所有节点,就开始处理下一层。
-
-
层与层之间的分隔: 在我的函数中,每处理完一层节点后,打印一个换行符,这样可以在输出中清楚地区分不同的层级。
-
销毁队列: 最后,当所有的节点都被访问过后,队列将会变空,遍历结束。此时,销毁或清空队列来释放资源。
通过这个过程,我的函数能够按层次顺序访问二叉树中的每个节点。这种遍历方式在很多场景中非常有用,例如在树的宽度优先搜索(Breadth-First Search, BFS)中。
结语
通过本文,我们不仅了解了二叉树的基本理论知识,还学习了如何在C语言中实现和操作这种数据结构。无论是对于初学者还是有经验的程序员来说,掌握这些知识都是非常有价值的。
相关文章:

深入探索C语言中的二叉树:数据结构之旅
引言 在计算机科学领域,数据结构是基础中的基础。在众多数据结构中,二叉树因其在各种操作中的高效性而脱颖而出。二叉树是一种特殊的树形结构,每个节点最多有两个子节点:左子节点和右子节点。这种结构使得搜索、插入、删除等操作…...

如何发现服务器被入侵了,服务器被入侵了该如何处理?
作为现代社会的重要基础设施之一,服务器的安全性备受关注。服务器被侵入可能导致严重的数据泄露、系统瘫痪等问题,因此及时排查服务器是否被侵入,成为了保障信息安全的重要环节。小德将给大家介绍服务器是否被侵入的排查方案,并采…...
CSDN一键注释功能
这是什么牛逼哄哄的功能 看这里: 然后: 再试一个: 输出结果是?package yuyi03.interview;/*** ClassName: InterviewTest2* Package: yuyi03.interview* Description:** Author 雨翼轻尘* Create 2023/12/14 0014 0:08*/ publ…...
基于JAVA的校园电子商城系统论文
摘 要 网络技术和计算机技术发展至今,已经拥有了深厚的理论基础,并在现实中进行了充分运用,尤其是基于计算机运行的软件更是受到各界的关注。加上现在人们已经步入信息时代,所以对于信息的宣传和管理就很关键。因此校园购物信息的…...
直播传媒公司网站搭建作用如何
直播已然成为抖快等平台的主要生态之一,近些年主播也成为了一种新行业,相关的mcn机构直播传播公司等也时有开业,以旗下主播带来高盈利,而在实际运作中也有一些痛点难题: 1、机构宣传展示难 不少散主播往往会选择合作…...

数据结构与算法-动态规划-机器人达到指定位置方法数
机器人达到指定位置方法数 来自左程云老师书中的一道题 【题目】 假设有排成一行的 N 个位置,记为 1~N,N 一定大于或等于 2。开始时机器人在其中的 M 位置上(M 一定是 1~N 中的一个),机器人可以往左走或…...
-docker的基本使用)
K8S学习指南(2)-docker的基本使用
文章目录 引言安装 DockerDocker 基本概念1. 镜像(Images)示例:拉取并运行一个 Nginx 镜像 2. 容器(Containers)示例:查看运行中的容器 3. 仓库(Repository)示例:推送镜像…...

java 执行linux 命令
文章目录 前言一、linux命令执行二、使用步骤三、踩坑 前言 java 执行linux 命令; 本文模拟复制linux文件到指定文件夹后打zip包后返回zip名称,提供给下载接口下载zip; 一、linux命令执行 linux命令执行Process process Runtime.getRunti…...
ubuntu将本机的wifi网络通过网线分享给另一台机器(用于没有有线网络,重装系统后无wifi驱动或者另一台设备没有wifi网卡)
1.将两台机器通过网线连接 2.在pci ethernet中设置选择另一台机器的mac address,ipv4中选择share to other computer,另一台机器上设置为动态ip,连接上之后另一台机器即可上网。...

Docker + Jenkins + Gitee 自动化部署项目
1.简介 各位看官老爷,本文为Jenkins实战,注重实际过程,阅读完会有以下收获: 了解如何使用Docker安装Jenkins了解如何使用Jenkins部署maven项目了解如何使用JenkinsGitee实现自动化部署 2.Jenkins介绍 相信,正在读这…...

ChatGPT 应用开发(一)ChatGPT OpenAI API 免代理调用方式(通过 Cloudflare 的 AI Gateway)
前言 开发 ChatGPT 应用,我觉得最前置的点就是能使用 ChatGPT API 接口。首先我自己要能成功访问,这没问题,会魔法就可以本地调用。 那用户如何调用到我的应用 API 呢,我的理解是通过用户能访问到的中转服务器向 OpenAI 发起访问…...

【TC3xx】GETH
目录 一、RGMII 二、SMI接口 三、TC3xx MCAL 3.1 MCU 3.2 Port 3.3 DMA 3.4 中断配置 3.5 ETH 3.6 集成 一、RGMII TC3xx支持MII/RMII/RGMII三种以太网数据通信接口。其中RGMII经常用于MAC和MAC之间,或MAC与PHY之间的通信,RGMII的带宽可以是10M…...
不需要联网的ocr项目
地址 GitHub - plantree/ocr-pwa: A simple PWA for OCR, based on Tesseract. 协议 mit 界面 推荐理由 可以离线使用,隐私安全...

【Git使用总结】
Git使用总结 随着软件开发和团队协作的日益重要,Git作为一种强大的版本控制系统,已经成为了开发人员不可或缺的工具。本文将对Git的使用进行总结,以帮助读者更好地掌握Git的用法和技巧。 一、Git的基本概念 在开始使用Git之前,…...

仿照MyBatis手写一个持久层框架学习
首先数据准备,创建MySQL数据库mybatis,创建表并插入数据。 DROP TABLE IF EXISTS user_t; CREATE TABLE user_t ( id INT PRIMARY KEY, username VARCHAR ( 128 ) ); INSERT INTO user_t VALUES(1,Tom); INSERT INTO user_t VALUES(2,Jerry);JDBC API允…...

关东升老师极简系列丛书(由清华大学出版社出版)
极简系列丛书,编程学习新体验 在这个科技日新月异的时代,编程已经成为了一种必备技能。但是面对各种复杂的编程语言,你是否也曾感到过迷茫和困惑?由清华大学出版社出版的“极简系列丛书”就是为了帮助你解决这个问题。 这套丛书…...

要求CHATGPT高质量回答的艺术:提示工程技术的完整指南—第 27 章:如何避开和绕过所有人工智能内容检测器
要求CHATGPT高质量回答的艺术:提示工程技术的完整指南—第 27 章:如何避开和绕过所有人工智能内容检测器 使用高易错性和突发性方法 与人工智能生成的文本相比,人类写作往往具有更多的突发性,这是由于人类往往比人工智能生成的文…...
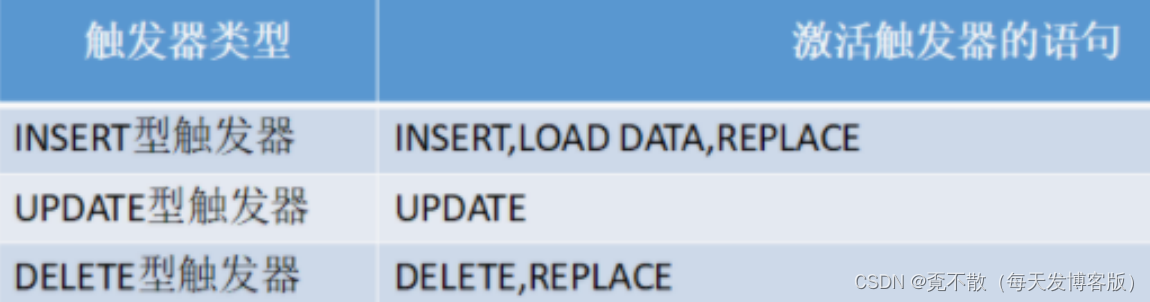
JavaWeb笔记之MySQL数据库
#Author 流云 #Version 1.0 一、引言 1.1 现有的数据存储方式有哪些? Java程序存储数据(变量、对象、数组、集合),数据保存在内存中,属于瞬时状态存储。 文件(File)存储数据,保存…...
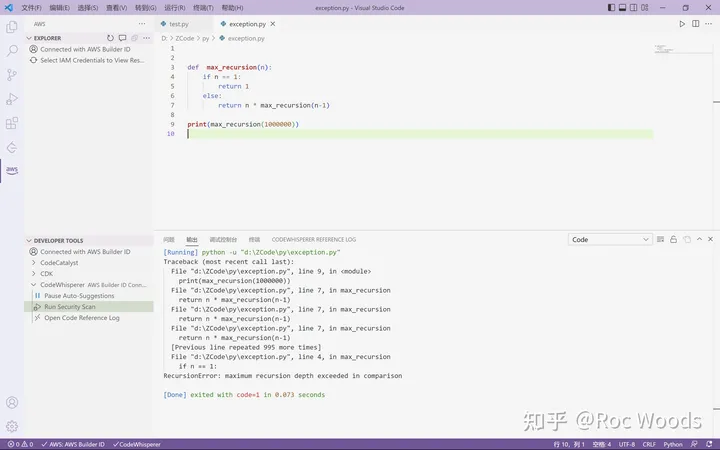
Amazon CodeWhisperer 开箱初体验
文章作者:Coder9527 科技的进步日新月异,正当人工智能发展如火如荼的时候,各大厂商在“解放”码农的道路上不断创造出各种 Coding 利器,今天在下就带大家开箱体验一个 Coding 利器: Amazon CodeWhisperer。 亚马逊云科…...

Java的引用类型有几种?区别是什么?
Java中的引用类型主要分为四种:强引用(Strong Reference)、软引用(Soft Reference)、弱引用(Weak Reference)和虚引用(Phantom Reference)。这些引用类型在Java中主要用于…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
