算法-只出现一次的数字集合
前言
仅记录学习笔记,如有错误欢迎指正。
题目
记录一道面试过的题目题目如下:
给定一个数组,内容为1-n的数字,其中每个数字只会出现一次或者多次,请在时间复杂度O(n),空间复杂度O(1)的条件下找出所有出现一次的数字集合。
例子:
输入:
1, 2, 3, 4, 5, 4, 3, 2
输出: 5,1
解释:
1,5只出现一次
代码
之前好像见过,但是没用心记录。
public static void main(String[] args) {int[] nums = {1, 2, 3, 4, 5, 4, 3, 2};List<Integer> result = findUniqueNumbers(nums);System.out.println("Unique numbers: " + result);}public static List<Integer> findUniqueNumbers(int[] nums) {List<Integer> result = new ArrayList<>();// 使用异或运算找到所有出现一次的数字int xor = 0;for (int num : nums) {xor ^= num;}// 找到异或结果中最低位的1int lowestBit = xor & -xor;// 根据最低位的1将数组分成两部分,分别进行异或运算int group1 = 0, group2 = 0;for (int num : nums) {if ((num & lowestBit) != 0) {group1 ^= num;} else {group2 ^= num;}}// 将出现一次的数字添加到结果列表中if (isUnique(group1, nums)) {result.add(group1);}if (isUnique(group2, nums)) {result.add(group2);}return result;}public static boolean isUnique(int num, int[] nums) {int count = 0;for (int n : nums) {if (n == num) {count++;}}return count == 1;}
相关文章:

算法-只出现一次的数字集合
前言 仅记录学习笔记,如有错误欢迎指正。 题目 记录一道面试过的题目 题目如下: 给定一个数组,内容为1-n的数字,其中每个数字只会出现一次或者多次,请在时间复杂度O(n),空间复杂度O(1)的条件下找出所有出现一次的数…...

Linux,Web网站服务(一)
1.准备工作 为了避免发生端口冲突,程序冲突等现象,建议卸载使用RPM方式安装的httpd [rootnode01 ~]# rpm -e http --nodeps 挂载光盘到/mnt目录 [rootnode01 ~]# mount /dev/cdrom /mnt Apache的配置及运行需要apr.pcre等软件包的支持,因此…...

Monkey工具之fastbot-iOS实践
背景 目前移动端App上线后 crash 率比较高, 尤其在iOS端。我们需要一款Monkey工具测试App的稳定性,更早的发现crash问题并修复。 去年移动开发者大会上有参加 fastbot 的分享,所以很自然的就想到Fastbot工具。 Fastbot-iOS安装配置 准备工…...

我想当个程序员
1、为什么当初选择计算机行业 能从事这个行业,也和当时经济情况有关系。 初中开始感兴趣,大学软件工程专业。大四报的android的培训,后来进的对日外包,没想到签合同当天被辞,非技术原因,性格导致。后来回家…...
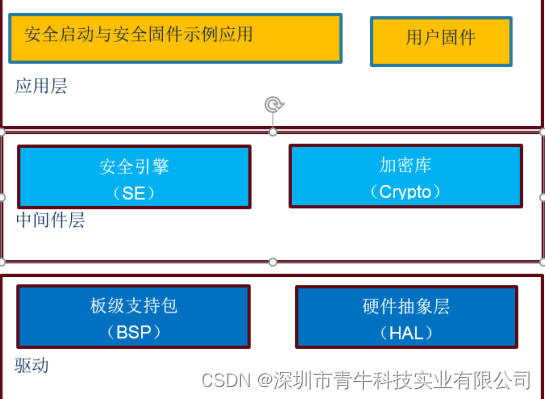
ACM32如何保护算法、协议不被破解或者修改
ACM32具有以下几种功能,可以保护算法、协议不被破解或者修改。 1.存储保护 RDP读保护 WRP写保护 PCROP 专有代码读保护 MPU存储区域权限控制 Secure User Memory存储区域加密 2.密码学算法引擎 AES HASH 随机数生成 …...
常用快捷键)
Android Studio(Flutter)常用快捷键
快捷键说明Ctrl Alt M抽取方法Ctrl Alt W抽取组件Alt Enter包裹组件Shift F6重命名Ctrl Alt L代码格式化Ctrl Alt O删除无用importCtrl X删除光标所在行Ctrl D复制一行代码Ctrl C复制Ctrl V粘贴Ctrl Z撤销Ctrl /注释一行代码Ctrl Shift /注释一段代码Ctrl S…...

CSS特效030:日蚀动画
CSS常用示例100专栏目录 本专栏记录的是经常使用的CSS示例与技巧,主要包含CSS布局,CSS特效,CSS花边信息三部分内容。其中CSS布局主要是列出一些常用的CSS布局信息点,CSS特效主要是一些动画示例,CSS花边是描述了一些CSS…...

746.使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。 请你计算并返回达到楼梯顶部的最低花费。 示例 1…...

【业务功能篇132】生产环境中出现oom问题,排查思路
1、使用dmesg命令查看系统日志 dmesg |grep -E ‘kill|oom|out of memory’,可以查看操作系统启动后的系统日志,这里就是查看跟内存溢出相关联的系统日志。 2、这时候,需要启动项目,使用ps命令查看进程 ps -aux|grep java命令查…...
如何将html网页免费转为excel?
一、直接复制。 直接复制是最简单有效、快捷的解决方案,操作方法如下: 1、用鼠标像平常复制文本一样,将整个网页表格选中。 2、点击右键,点击“复制”。 3、打开excel软件,鼠标点击任意单元格。 4、点击右键&#…...

手撕分布式缓存---HTTP Server搭建
经过了前两个章节的学习,分布式缓存的存储与新增我们已经实现了,并且对其做了高可用处理。本章节我们剥离和缓存强相关的逻辑,开始搭建一个HTTP服务器,毕竟缓存数据库搭建完之后别人没法访问也是没有用处的。这一章节我们重点学习…...

2. PyTorch——Tensor和Numpy
2.1Tensor和Numpy Tensor和Numpy数组之间具有很高的相似性,彼此之间的互操作也非常简单高效。需要注意的是,Numpy和Tensor共享内存。由于Numpy历史悠久,支持丰富的操作,所以当遇到Tensor不支持的操作时,可先转成Numpy…...
使用小计)
C#随笔 | List.Sort()使用小计
1、使用List.Sort()对基本数值类型数据进行排序 案例:对存放int数据的List进行排序 其实C#中的List的Sort函数中的比较函数CompareTo有三种结果 1, -1 ,0分别代表大,小,相等。默认List的排序是升序排序。 举个例子:在比较函数Co…...

【WebRTC】用WebRTC做即时视频聊天应用
【配套项目源码】 打开即用,设置一个免费的Agora账户就可以实现视频电话。非常好的WebRTC学习和应用项目。 用VSCode打开即可。 https://download.csdn.net/download/weixin_41697242/88630069 【什么是WebRTC?】 WebRTC是一套基于JS的API,能够建立端对端的直接通信,实…...
GPT-4.5 要来了!谷歌大模型 Gemini 确实给够压力
GPT-4 还没用明白,GPT-4.5 就要发布了。 最近,OpenAI 泄露了 GPT-4.5 的发布页面,除了进一步增强复杂推理和跨模态理解,GPT-4.5 增加了一个更加强大的功能——3D。 3D 功能的进一步支持,也就意味着多模态最后一块版图…...

美易官方:加密资产将破坏金融稳定,无法取消就要加强监管
在近日的一次公开演讲中,国际货币基金组织(IMF)总裁格奥尔基耶娃表示,如果世界各国大量采用加密资产,将会对金融稳定造成破坏,并且无法取消这种破坏,因此需要加强对加密资产的监管。我们的目标是…...
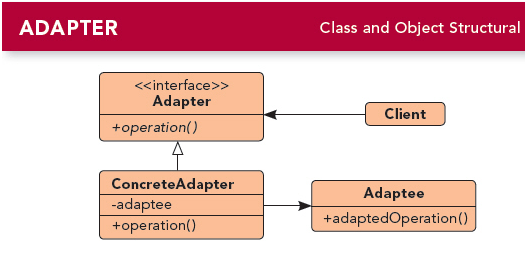
一文读懂Java中的设计模式——适配器模式,对于兼容不同系统特别适用!
适配器模式概念 适配器(变压器)模式:这种模式的核心是当你想实现一个接口但又不想实现所有接口方法,只想去实现一部分方法时,就用默认的适配器模式,他的方法是在接口和具体实现类中添加一个抽象类…...
2023年国内外评分前十的项目管理软件推荐
1、进度猫 作为国产项目进度管理软件新秀,是一款以甘特图为向导的轻量级可视化在线项目管理工具 通过甘特图/思维导图为核心进行项目管理计划,使项目经理能够计划、可视化目标和里程碑、设置任务和到期日期。 甘特图进行有序的项目规划,及…...

3.electron之vue3.0的桌面应用程序
如果可以实现记得点赞分享,谢谢老铁~ Electron是一个使用 JavaScript、HTML 和 CSS 构建桌面应用程序的框架。 Electron 将 Chromium 和 Node.js 嵌入到了一个二进制文件中,因此它允许你仅需一个代码仓库,就可以撰写支持 Windows、…...
二十二 使用opencv进行人脸、眼睛、嘴的检测)
数字图像处理(实践篇)二十二 使用opencv进行人脸、眼睛、嘴的检测
目录 1 xml文件 2 涉及的函数 3 实践 使用opencv进行人脸、眼睛、嘴的检测。 1 xml文件 方法① 下载 地址:https://github.com/opencv/opencv/tree/master/data/haarcascades 点击haarcascade_frontalface_default.xml文件 对着Raw右键,选择“链接另存为”,选择代码所…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
