R语言,table()函数实现统计每个元素出现的频数+并将最终统计频数结果转换成dataframe数据框形式
在 R中,要统计dataframe数据框中每个元素出现的频数,可以使用`table()`函数。以下是一个示例:
目录
一、创建数据
二、统计第一列每个元素出现的频数
三、统计第二列每个元素出现的频数
四、将频数结果转换为数据框,并改列名
一、创建数据
# 创建一个示例数据框
data <- data.frame(col1 = c("A", "E", "A", "E", "B", "E", "E", "B", "B"),col2 = c(4, 5, 6, 5, 4, 6, 4, 5, 6))结果如下:

二、统计第一列每个元素出现的频数
# 统计每个元素出现的频数
frequency_table1 <- table(data$col1)# 输出频数统计结果
print(frequency_table1)结果如下:

三、统计第二列每个元素出现的频数
# 统计每个元素出现的频数
frequency_table2 <- table(data$col2)# 输出频数统计结果
print(frequency_table2)结果如下:

四、将频数结果转换为数据框,并改列名
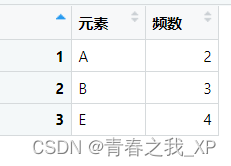
frequency_dataframe <- as.data.frame(frequency_table1)colnames(frequency_dataframe) <- c("元素","频数")结果如下:
相关文章:

R语言,table()函数实现统计每个元素出现的频数+并将最终统计频数结果转换成dataframe数据框形式
在 R中,要统计dataframe数据框中每个元素出现的频数,可以使用table()函数。以下是一个示例: 目录 一、创建数据 二、统计第一列每个元素出现的频数 三、统计第二列每个元素出现的频数 四、将频数结果转换为数据框,并改列名 一…...

微信小程序uniapp记住密码
记住密码功能 在请求登录接口成功后,我们需要判断用户是否勾选记住密码,如果是,则将记住密码状态、账号信息存入本地。 下次登录时,获取本地的记住密码状态,如果为true则获取本地存储的账号信息,将信息回填…...
喜报!Coremail荣获2023信创“大比武”优秀生态融合奖
近期,2023信创“大比武”金融业务创新应用赛道(简称金融赛道)活动正式落下帷幕。经过赛程的层层考核,中泰证券股份有限公司(简称“中泰证券”)与Coremail联合组成的“中泰证券CACTER邮件安全保卫队”最终在…...
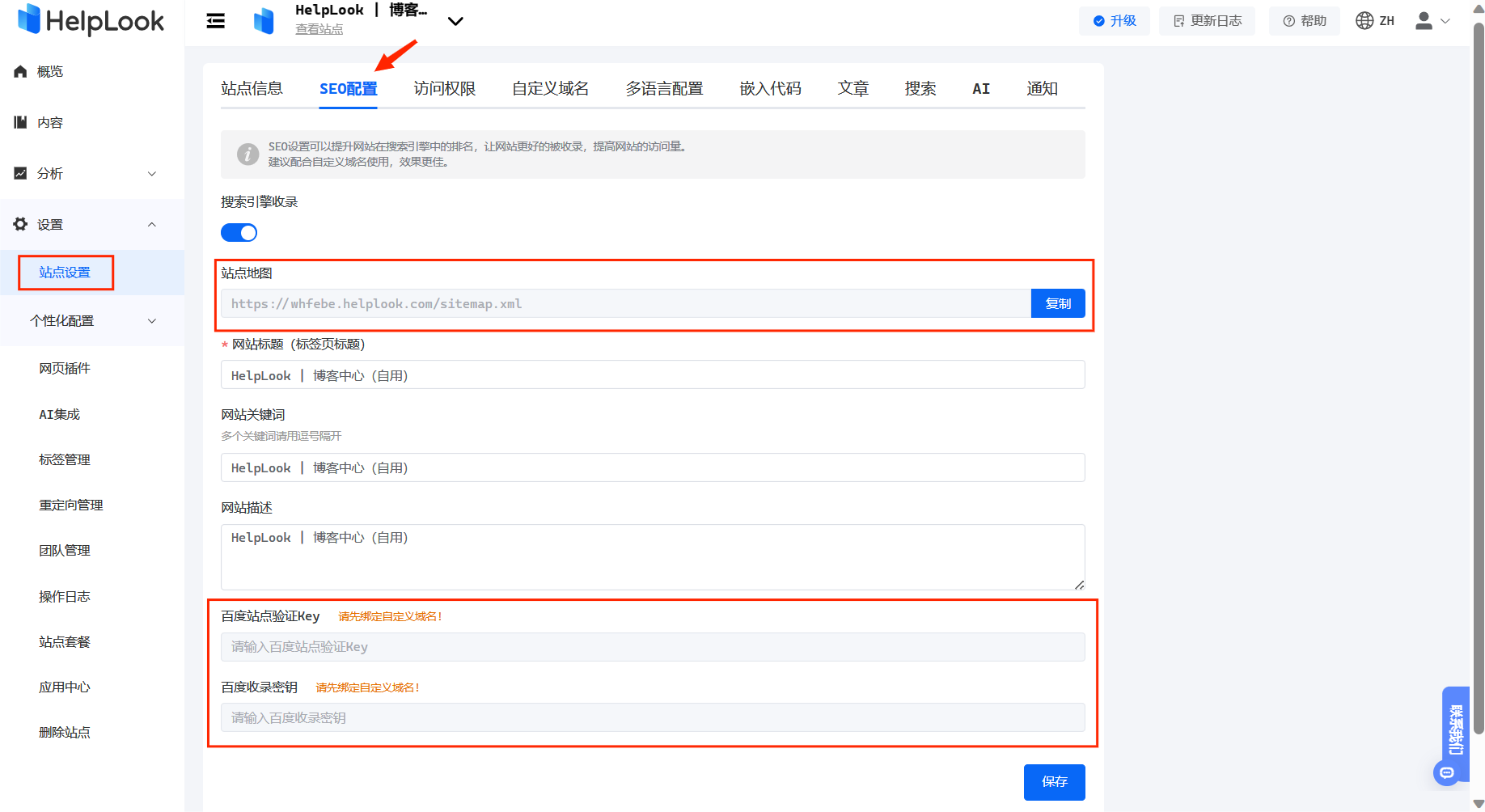
知识库SEO:提升网站内容质量与搜索引擎排名的策略
随着搜索引擎算法的不断更新和优化,单纯依靠关键词堆砌和外部链接的时代已经过去。现在的SEO(搜索引擎优化)已经转向了以提供高质量、有价值内容为核心的阶段。知识库SEO便是这个新阶段的重要策略之一。 | 一、知识库SEO的概念与意义 1.定义…...

GPIO复用时5个调试接口引脚要注意
一、JTAG引脚作为GPIO使用要注意 例如PA15引脚,它默认时JTDI引脚,但是可以复用为SPI的NSS片选信号。在初始化时,需要先开启AFIO时钟,再关闭JTAG功能,否则GPIO功能仍然不起作用。初始化代码如下: stm32f10…...

华为云CodeArts Check常见问答汇总
1.【Check】如何查看代码检查的历史记录呢? 答:当前支持查看代码检查日志的历史记录,具体操作步骤: 1、进入代码检查页面,在任务列表中,单击任务名称。 2、进入“代码检查详情”页面,选择“…...
linux 应用开发笔记---【信号:基础】
1.基本概念 信号是发生事件时对进程的通知机制,也可以称为软件中断 信号的目的是用来通信的 1.硬件发生异常,将错误信息通知给内核,然后内核将相关的信号给相关的进程 2.在终端输入特殊字符产生特殊信号 3.进程调用kill()将任意信号发送…...

区块链:改变世界的技术
一、引言 区块链,这个曾经看似神秘且遥不可及的词语,如今已经深入人心,成为我们生活的一部分。它以其独特的去中心化、分布式、不可篡改的特性,正在改变我们的生活方式,甚至改变我们的思维方式。本文将深入浅出地解释…...
防御升级!SMC2助力企业高效应对邮箱安全挑战
根据Coremail邮件安全人工智能实验室(以下简称AI实验室)的监测数据显示,2023年Q3全国企业级用户遭受无差别的暴力破解攻击次数虽相比2022年同期有所下降,但仍高达 24.2 亿次,且暴力破解攻击次数有明显回升趋势。 面对正…...

19.(vue3.x+vite)v-if和v-for哪个优先级更高
前端技术社区总目录(订阅之前请先查看该博客) v-if和v-for哪个优先级更高 (1)实践中不应该把v-for和v-if放一起,可以包一层template (2)在vue2中,v-for的优先级是高于v-if (3)在vue3中,v-for的优先级是低于v-if 组件代码 <template><div><!--包一…...

12. IO
1.File类 • File 类代表与平台无关的文件和目录。 • File 能新建、删除、重命名文件和目录,但 File 不能访问文件内容本身。如果需要访问文件内容本身,则需要使用输入/输出流。 1).File的常用方法 在这里插入图片描述 2).遍历给定目录所有文件 …...

【稳定检索|投稿优惠】2024年艺术鉴赏与社会科学教育国际会议(ICAASSE 2024)
2024年艺术鉴赏与社会科学教育国际会议(ICAASSE 2024) 2024 International Conference on Art Appreciation and Social Science Education(ICAASSE) 一、【会议简介】 2024年艺术鉴赏与社会科学教育国际会议(ICAASSE 2024),这场学术盛宴,将于2024年2月1…...

leetCode算法—3.无重复字符的最长子串
1.给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s “abcabcbb” 输出: 3 解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。 示例 2: 输入: s “bbbbb” 输出: 1 解释: 因为无重复字符的最长子串是 …...
STM32 寄存器配置笔记——USART DMA接收
一、简介 本文主要介绍STM32如何配合USART的IDLE中断实现USART DMA接收不定长的数据。其中使用的接收缓存还是延用前面博客写的乒乓缓存。使用DMA USART接收来替代中断方式或轮询方式的接收主要是为了提高代码的运行效率,中断方式的接收,每接收一个字节便…...

(基础篇)通过node增删改查连接mysql数据库
一定要会最基础的sql建表一定要会最基础的sql建表一定要会最基础的sql建表 首先说一下准备工作 一、准备工具 1.mysql数据库Navicat可视化工具(数据库表单已经建好) 我这里用的小皮工具直接开启的本地mysql 2.vscode (不用说基本上都有) 3.node.js …...

做为一个产品经理带你详细了解--动态面板的使用
📚📚 🏅我是bing人,一个在CSDN分享笔记的博主。📚📚 🌟在这里,我要推荐给大家我的专栏《Axure》。🎯🎯 🚀无论你是编程小白,还是有一…...

严世芸龟法养生经
文章目录 严世芸理念荤素搭配,不偏嗜动静结合心平气和 龟息法 严世芸 严世芸,出生于1940年,现任上海中医药大学的主任医师,教授。他父亲是近代上海有名的中医,他又是著名医家张伯臾的亲传弟子。 从小就在父亲诊室里长…...
基于OHTPPS实现网站HTTPS访问
前言 笔者近期为网站配置HTTPS的域名,查找了大量方案,最近寻得一个不错的解决方式,通过OHTTPS获取免费的证书并部署到阿里云服务器上。 步骤 到OHTTPS官网注册账号 官方地址如下,读者可以先行到官网注册一下账号,笔…...

python|获取接口请求耗时
你想知道我们请求一个url的时候,握手和请求资源分别占用多长时间么?今天我们使用python写个小案例来看看吧。 项目展示 打开项目,修改hosts、port、methods以及url的变量,即可运行python程序便可获得该页面的详细信息的时间&…...

[PyTorch][chapter 7][李宏毅深度学习][深度学习简介]
前言: 深度学习常用的开发平台 TensorFlow torch theano caffe DSSTNE mxnet libdnn CNTK 目录: 1: 深度学习发展历史 2: DeepLearning 工程简介 3: DNN 简介 一 发展历史 二 DeepLearning 工程简介 深度学习三…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...
