[Linformer]论文实现:Linformer: Self-Attention with Linear Complexity
文章目录
- 一、完整代码
- 二、论文解读
- 2.1 介绍
- 2.2 Self-Attention is Low Rank
- 2.3 模型架构
- 2.4 结果
- 三、整体总结
论文:Linformer: Self-Attention with Linear Complexity
作者:Sinong Wang, Belinda Z. Li, Madian Khabsa, Han Fang, Hao Ma
时间:2020
模型结构较于简单,证明有点难,有时间可以做一下文章的证明分析;
一、完整代码
这里我们使用python代码进行实现
# 完整代码在这里
# 模型结构较于简单,有时间再弄
二、论文解读
2.1 介绍
这是一篇介绍transformer的优化模型的论文,其对普通的transformer模型进行了优化,把时间复杂度和空间复杂度都从 O ( n 2 ) O(n^2) O(n2)降低为了 O ( n ) O(n) O(n);论文推出的模型叫Linformer,其主要思想利用到了两个思想,一个是the distributional Johnson–Lindenstrauss lemma, the Eckart–Young–Mirsky Theorem;这两个思想一同证实了利用降维去构造一个低秩矩阵来降低复杂度的可行性;
为什么要改进transformer模型:计算量太大,价格昂贵,操作复杂度为 O ( n 2 ) O(n^2) O(n2);部署困难,并不容易进行推理;
目前的其他降维方法:Sparse transformer利用Sparse matrix;Reformer利用locally-sensitive hashing (LSH),并且只有序列长度大于2048的时候才有用;
不同模型架构方法对比如下:

相比于图中的模型,Linformer在复杂度和操作上是最佳的;
在这里提一下Transformer的自注意力机制,这都是非常基础了;

提高transformer的效率有很多种办法,下面简单介绍几种:
Mixed Precision:使用半精度或混合精度表示,即采用量化的方式加快计算;
Knowledge Distillation:和DistillBERT一样,利用学生模型去学习教师模型的分布预测;
Sparse Attention:只计算对角线部分的注意力权重;
该技术通过在上下文映射矩阵
P中添加稀疏性来提高自我注意的效率。例如,sparse transformer只计算矩阵P的对角线附近的Pij(而不是所有的Pij)。同时,block-wise self-attention将P划分为多个块,只计算所选块内的Pij。然而,这些技术也遭受了很大的性能下降,同时只有有限的额外加速,即下降2%,加速20%。
LSH Attention:操作复杂,有效果但是有限制;
Locally-sensitive hashing(LSH)注意在计算点积注意时采用了多轮哈希方案,在理论上将自注意复杂度降低到O(n log(n))。然而,在实践中,它们的复杂度项有一个很大的常数1282,并且只有当序列长度非常长时,它才比普通的变压器更有效。
Improving Optimizer Efficiency:没注意过,不出名;
Microbatching将一批分成小的微批(可以放入内存),然后通过梯度积累分别向前和向后运行。Gradient checkpointing仅通过缓存一个图层子集的激活来节省内存。在从最新的检查点进行反向传播期间,将重新计算未缓存的激活。这两种技术都可以利用时间来换取内存,而且都不能加快推理的速度。
2.2 Self-Attention is Low Rank
如标题,这节主要证明了self-attention其实是一个低秩矩阵;
作者使用了两个预训练的transformer模型,RoBERTa-base和RoBERTa-large,前者是12层的模型,后者是24层的模型;
作者通过对每一层的特征值进行分解,然后做图如下,纵坐标代表归一化的累积特征值,由于序列长度是512维的,所以一个有512个特征值;
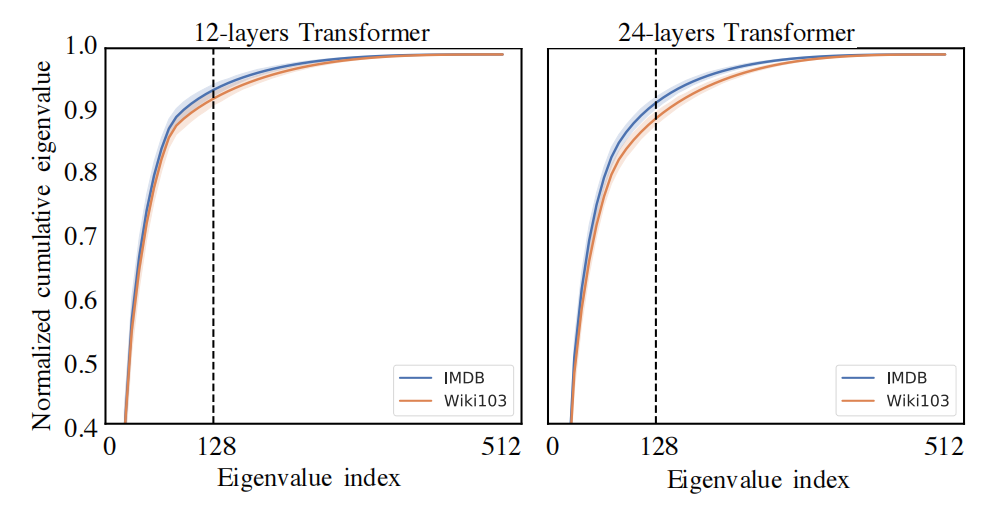
通过观察发现,当取前面128个较大的特征值时,累积特征值已经到达了95%,通过主成分可以直到,前面128个较大的特征值可以表示整体的95%的信息,所以我们可以对其使用奇异值分解的方式降低维度从而达到降低复杂度的目的;
下图是不同层次的累积贡献度的谱分布,如下:

从上图中我们可以发现:高层的谱分布比下层更倾斜,这意味着在高层,更多的信息集中在最大奇异值,导致了P的秩相较于底层较低;
这里利用两个思想,一个是the distributional Johnson–Lindenstrauss lemma, the Eckart–Young–Mirsky Theorem;前者证明出现高维矩阵是低秩矩阵这种现象是正常的,后者表示奇异值分解在相同的维度下获得低秩矩阵的绝大部分信息;而奇异值分解是相当需要计算量的,高维矩阵分解操作起来很复杂,这里论文中使用投影的方式解决了这一问题;
2.3 模型架构
直接看下面这张图,就知道作者做了什么处理:

在Linear层得到了 Q , K , V Q,K,V Q,K,V后,为了降低 K , V K,V K,V的维度,其使用了投影到低维的方式,具体公式如下:

之前 Q W , K W , V W QW,KW,VW QW,KW,VW都是一个n·d_model的矩阵,在这里有 E i , F i E_i,F_i Ei,Fi都是一个k·n的矩阵,有前面的softmax变成了一个 n·k的矩阵,后者是一个k·d的矩阵,这里的空间复杂度为 O ( k n + 2 k d ) O(kn + 2kd) O(kn+2kd),把平方项降低为一次项;如果我们可以选择一个非常小的投影维数k,即kn,那么我们就可以显著地减少内存和空间消耗;
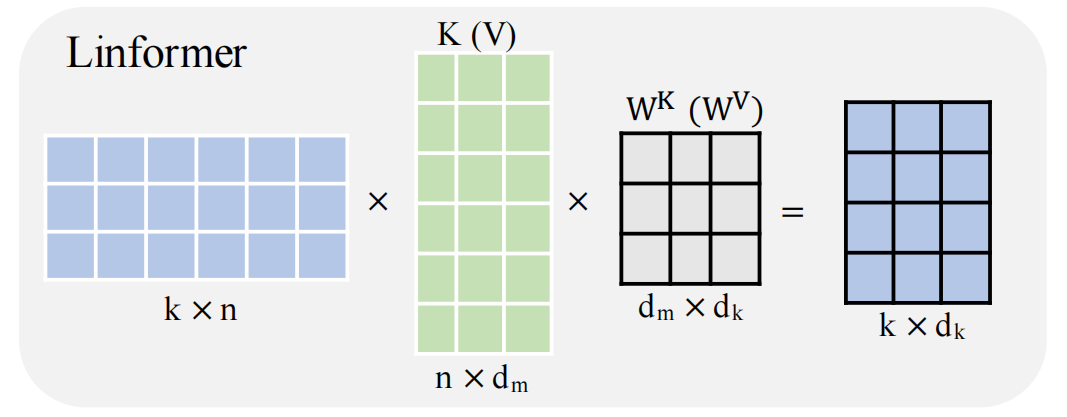
从下图,我们可以发现设置的k越小,推理速度越快;

这和预期一致;
继续优化可以采用方法:
Parameter sharing between projections:即共享投影层的参数,
- 头之间共享:在每一层中的投影矩阵 E , F E,F E,F中,我们共享两个投影矩阵 E i E_i Ei和 F i F_i Fi,确保在每一个头 i i i中,有 E i = E , F i = F E_i=E,F_i=F Ei=E,Fi=F;
- K , V K,V K,V之间共享:在每一层中的投影矩阵 E , F E,F E,F中,我们共享两个投影矩阵 E i E_i Ei和 F i F_i Fi并化为一个矩阵,确保在每一个头 i i i中,有 E i = F i = E E_i=F_i=E Ei=Fi=E;
- 层与层之间共享:在所有的层中,对于所有的头部,对于所有的键和值,都使用一个投影矩阵 E E E;
Nonuniform projected dimension:不均匀投影,意思是结合不同层的低秩矩阵的秩,如上文我们可以得到高层的秩要比底层的秩要小,所以我们可以在高层设置较小的k在低层设置较大的k;
General projections: 我们可以采用其他的机制来缩小维度,而不是利用一个简单的投影的方式,例如均值池化,最大池化,卷积等等方式来缩小维度代替简单投影;
2.4 结果
论文中的结果可视化如下:

接下来对结果做一些解释:
a,b两图作者做了ppl曲线来判断模型的效果,在 n = 512 n=512 n=512时,随着k的增加,模型越来越贴近standard transformer曲线,有的模型甚至超过了;在 n = 1024 n=1024 n=1024时,表现了相同的趋势,但是同时可以发现,效果是非常贴近于标准模型的;
c图中,使用了三种参数共享策略来检验模型结果,可以发现参数共享并不会产生较大的影响,所以我们可以在模型中使用参数贡献,在保存相同的效果下,减少模型的参数;
d图中随着序列长度的增加,投影维数保持不变,收敛后的最终ppl仍然保持大致相同。而且不同曲线之间的间隔大小似乎相等,说明这是线性的;

下游任务模型效果,可以发现模型效果有些甚至超过了BERT和DistillBERT;
从模型 n = 1024 , k = 256 n = 1024,k = 256 n=1024,k=256和模型 n = 512 , k = 256 n = 512,k = 256 n=512,k=256效果一致可以看出来,模型的效果由预测维度k而不是比率n/k决定;
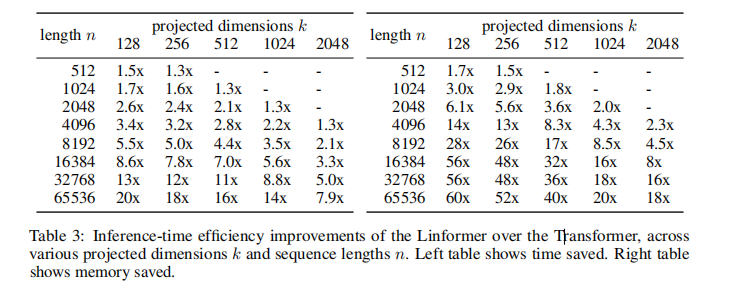
这是推理时间效果和空间复杂度效果的对比,可以看到Linformer可以在保持效果的情况下,大大优化时间和空间复杂度;
三、整体总结
这是一篇介绍transformer的优化模型的论文,其对普通的transformer模型进行了优化,把时间复杂度和空间复杂度都从 O ( n 2 ) O(n^2) O(n2)降低为了 O ( n ) O(n) O(n);论文推出的模型叫Linformer,其主要思想利用到了两个思想,一个是the distributional Johnson–Lindenstrauss lemma, the Eckart–Young–Mirsky Theorem;这两个思想一同证实了利用降维去构造一个低秩矩阵来降低复杂度的可行性;
相关文章:

[Linformer]论文实现:Linformer: Self-Attention with Linear Complexity
文章目录 一、完整代码二、论文解读2.1 介绍2.2 Self-Attention is Low Rank2.3 模型架构2.4 结果 三、整体总结 论文:Linformer: Self-Attention with Linear Complexity 作者:Sinong Wang, Belinda Z. Li, Madian Khabsa, Han Fang, Hao Ma 时间&#…...
【Jeecg Boot 3 - 第二天】1.1、后端 docker-compose 部署 JEECGBOOT3
一、场景 二、实战 ▶ 2.1 修改配置文件 > 目的一:将 dev 变更为生产环境 prod > 目的二:方便spring项目调用docker同个network下的redis和mysql ▶ 2.2 编写dockerfile ▶ 2.3 编写docker-compose.yaml ▶ 2.4 打…...

Centos单用户模式修改root密码
在CentOS 7的单用户模式下,你可以按照以下步骤修改root用户密码: 启动CentOS 7并进入GRUB菜单。在启动时按下任意键进入GRUB菜单。 在GRUB菜单中,选择要启动的CentOS 7内核版本,并按下e键进行编辑。 找到以 ro 开头的行…...
[Unity]关于Unity接入Appsflyer并且打点支付
首先需要去官方下载Appsflyer的UnityPackage 链接在这afPackage 然后导入 导入完成 引入此段代码 using AppsFlyerSDK; using System.Collections; using System.Collections.Generic; using UnityEngine;public class AppflysManager : MonoBehaviour {public static App…...

AICore 带来了 Android 专属的 AI 能力,它要解决什么?采用什么架构思路?
前言 Google 最近发布的 Gemini 模型在全球引起了巨大反响,其在多模态领域的 Video demo 无比震撼。对于 Android 开发者而言,其中最振奋人心的消息莫过于 Gemini Nano 模型将内置到 Android 系统当中,并开放给开发者使用。 事实上…...
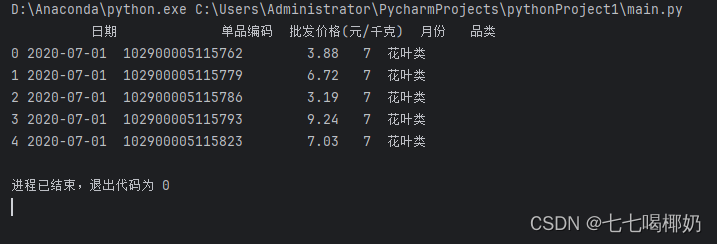
python学习1
大家好,这里是七七,今天开始又新开一个专栏,Python学习。这次思考了些许,准备用例子来学习,而不是只通过一大堆道理和书本来学习了。啊对,这次是从0开始学习,因此大佬不用看本文了,小…...

【SpringBoot】Spring Boot 单体应用升级 Spring Cloud 微服务
Spring Cloud 是在 Spring Boot 之上构建的一套微服务生态体系,包括服务发现、配置中心、限流降级、分布式事务、异步消息等,因此通过增加依赖、注解等简单的四步即可完成 Spring Boot 应用到 Spring Cloud 升级。 Spring Boot 应用升级为 Spring Cloud…...
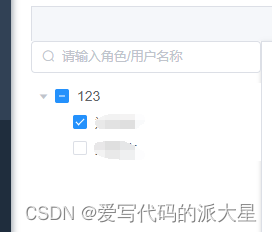
el-tree搜索的使用
2023.12.11今天我学习了如何对el-tree进行搜索的功能,效果如下: 代码如下: 重点部分:给el-tree设置ref,通过监听roleName的变化过滤数据。 default-expand-all可以设置默认展开全部子节点。 check可以拿到当前节点的…...
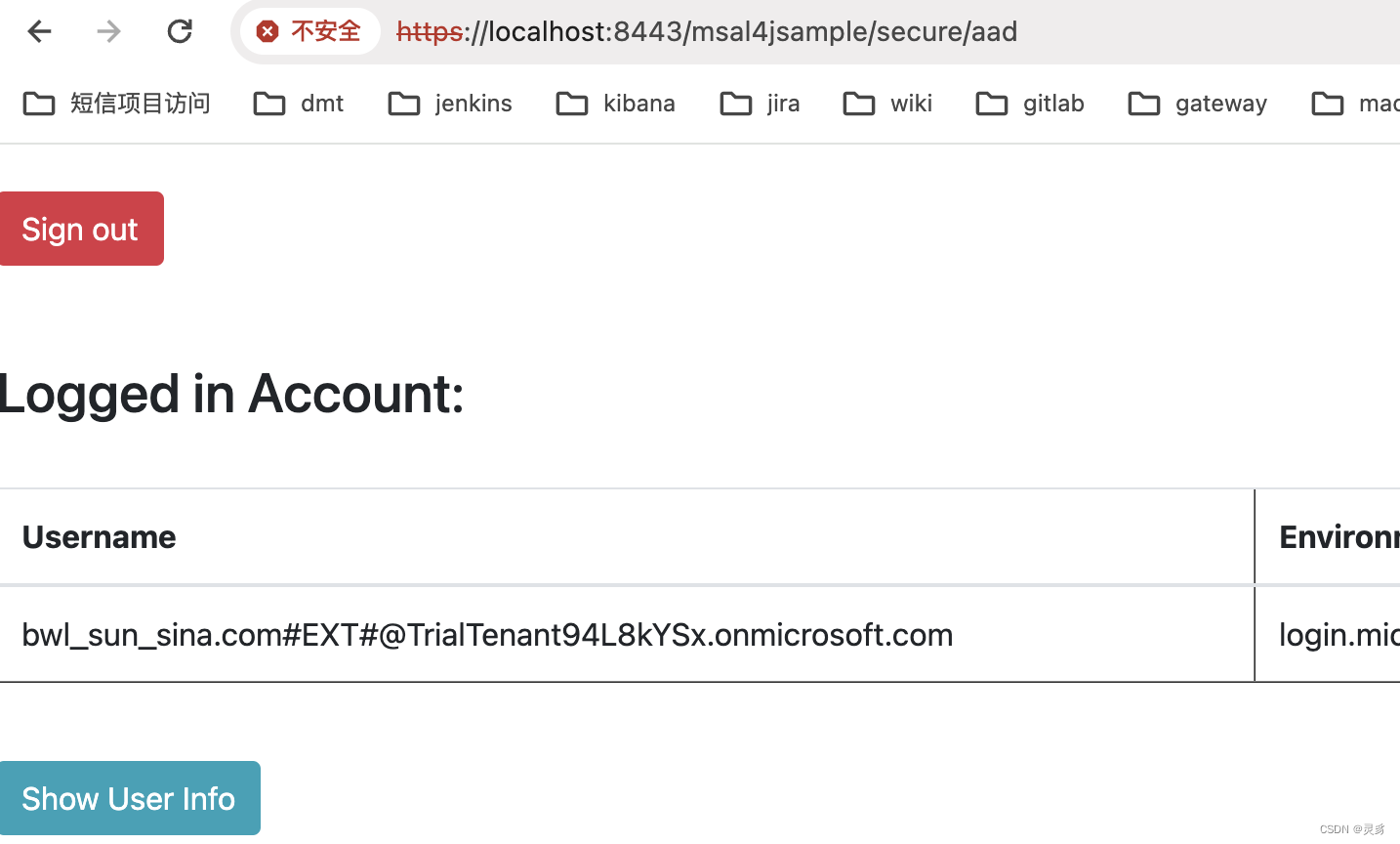
Java使用Microsoft Entra微软 SSO 认证接入
1. Microsoft Entra Microsoft Entra ID 是基于云的标识和访问管理服务,可帮助员工访问外部资源。 示例资源包括 Microsoft 365、Azure 门户以及成千上万的其他 SaaS 应用程序。 Microsoft Entra ID 还可帮助他们访问你的企业 Intranet 上的应用等内部资源&#x…...
)
“华为杯”研究生数学建模竞赛2016年-【华为杯】A题:无人机在抢险救灾中的优化运用(附获奖论文及MATLAB代码实现)
目录 摘 要: 1. 问题重述 1.1. 问题背景 1.2. 需要解决的问题 1.2.1....

17--异常处理
1、异常概述 1.1 什么是异常 异常:指的是程序在执行过程中,出现的非正常情况,如果不处理最终会导致JVM的非正常停止。 异常指的并不是语法错误和逻辑错误。语法错了,编译不通过,不会产生字节码文件,根本运…...
)
数据结构 | c++编程实现求二叉树的叶节点的个数。(递归非递归)
目录 非递归 递归 非递归 #include<iostream> #include<stack> using namespace std; struct BTNode {int data;BTNode* left, * right;BTNode(int val) :data(val), left(NULL), right(NULL) {}}; //递归的方式求二叉树的叶子结点数 int countnode(BTNode* t) …...

python读取csv文件
在Python中,你可以使用pandas库来读取CSV文件。以下是一个基本的例子: import pandas as pd# 读取CSV文件data pd.read_csv(filename.csv)# 显示前几行数据print(data.head()) 这里,filename.csv应该被替换为你的CSV文件的实际路径和名称。…...

租一台服务器多少钱决定服务器的价格因素有哪些
租一台服务器多少钱决定服务器的价格因素有哪些 大家好我是艾西,服务器这个名词对于不从业网络行业的人们看说肯定还是比较陌生的。在21世纪这个时代发展迅速的年代服务器在现实生活中是不可缺少的一环,平时大家上网浏览自己想要查询的信息等都是需要服…...
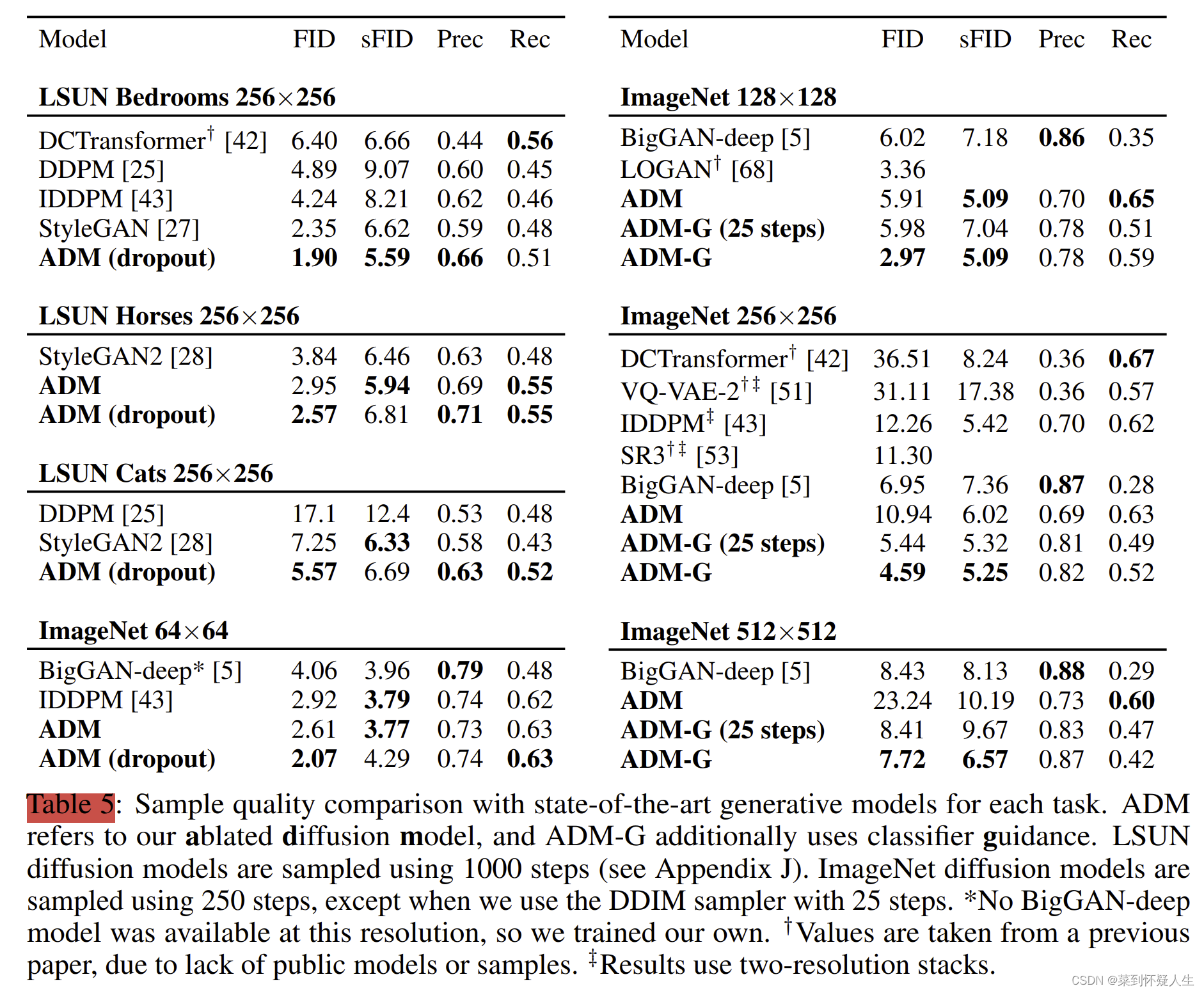
深度学习(生成式模型)——ADM:Diffusion Models Beat GANs on Image Synthesis
文章目录 前言基础模型结构UNet结构Timestep Embedding关于为什么需要timestep embedding global attention layer 如何提升diffusion model生成图像的质量Classifier guidance实验结果 前言 在前几篇博文中,我们已经介绍了DDPM、DDIM、Classifier guidance等相关的…...

Ubuntu无法解析域名DNS指向127.0.0.53问题处理
用nslookup 域名.com返回127.0.0.53无法解析错误 error"Could not lookup srv records on xxx.com: lookup xxx.com on 127.0.0.53:53: no such host" #首次尝试编辑/etc/resolved.conf文件DNS为8.8.8.8 或1.1.1.1 发现reboot重启后又恢复到127.0.0.53的内容#再次尝…...
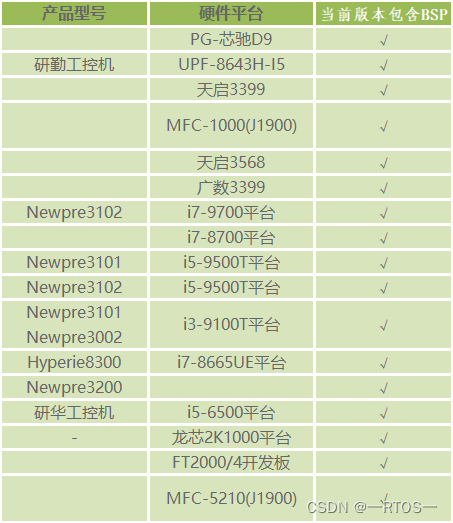
Intewell-Hyper I_V2.0.0_release版本正式发布
新型工业操作系统_Intewell-Hyper I_V2.0.0_release版本正式发布 软件发布版本信息 版本号:V2.0.0 版本发布类型:release正式版本 版本特点 1.建立Intewell-Hyper I基线版本 版本或修改说明 基于Intewell-Lin V2.3.0_release版本: 1.Devel…...

Mysql mybatis 语法示例
service package com.ruoyi.goods.service;import java.util.List; import com.ruoyi.goods.domain.GoodsProducts;/*** 商品Service接口* * author ruoyi* date 2023-08-27*/ public interface IGoodsProductsService {/*** 查询商品* * param ProductID 商品主键* return 商…...

第77讲:二进制方式搭建MySQL数据库5.7版本以及错误日志管理
二进制方式搭建MySQL数据库5.7版本 前面是使用的yum的方式安装的MySQL数据库,在企业生产环境中大多数都用二进制方式安装。 本次使用二进制方式搭建MySQL 5.7.36版本。 1.二进制安装MySQL5.7版本 1.1.下载MySQL5.7版本的二进制文件 [root@mysql ~]# wget https://downloads.…...
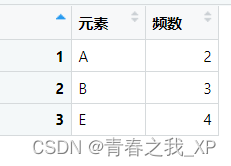
R语言,table()函数实现统计每个元素出现的频数+并将最终统计频数结果转换成dataframe数据框形式
在 R中,要统计dataframe数据框中每个元素出现的频数,可以使用table()函数。以下是一个示例: 目录 一、创建数据 二、统计第一列每个元素出现的频数 三、统计第二列每个元素出现的频数 四、将频数结果转换为数据框,并改列名 一…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
