2020年第九届数学建模国际赛小美赛A题自由泳解题全过程文档及程序
2020年第九届数学建模国际赛小美赛
A题 自由泳
原题再现:
在所有常见的游泳泳姿中,哪一种最快?哪个冲程推力最大?在自由泳项目中,游泳者可以选择他们的泳姿,他们通常选择前面的爬行。然而,游泳运动员是否有可能进一步提高他们的划水速度?请用一个数学模型来分析中风和指导运动员的训练。
整体求解过程概述(摘要)
游泳是生活中常见的一种运动形式,那么,在各种泳姿中,哪种泳姿能获得最大的速度或最大的推进力呢?是否有可能在爬行的基础上进行改进,进一步提高游泳速度?本文结合水动力公式对上述问题进行了讨论。
对于问题一,我们首先从几何上抽象出人体的形状,将手臂视为一个统一的圆柱体,将腿部视为两个圆柱体的组合。然后对四种泳姿的动作进行分析。根据流体力学中的阻力公式,将动阻力和静阻力分别表示,其中动阻力假定为全部推进力,腿的推进力作为补偿项。然后,根据牛顿第二定律的公式,建立了行驶速度随运动频率和时间变化的偏微分方程。在求解方程时,以运动频率为常数,将偏微分方程转化为常微分方程。然后利用四阶Runge-Kutta方法求解该方程,得到旅行速度与时间的定量关系。经过比较,我们发现自由泳是四种游泳方式中速度最快的。在30s内向前距离可达53.852m,比最慢蛙泳远14m左右。在推进力比较中,蝶泳在稳态下最大推进力可达150N左右,比最小仰泳大95N左右。
对于问题二,首先,在人类几何的抽象中,我们将手臂细化为上臂、前臂和手。以运动频率为常数,以上臂与肩线夹角、前臂与水平面夹角为变量,建立了运动速度与时间的偏微分方程。为了便于求解,我们假设两个角度在一次游泳中保持不变。然后将偏微分方程转化为常微分方程,采用固定步长搜索法遍历各角度求解,得到当两个角度均为0.5∏时的最大旅行速度,即当手臂伸直且手臂运动平面垂直于水平面时,可以得到最大旅行速度。最后,我们发现人体可以在27秒内以最大速度前进58.25米。为了保证模型的准确性,我们还进行了敏感性分析,证明了直臂划水是不同身体特征运动员的最佳划水。此外,我们还考虑了手指夹角对移动速度的影响,确定了当双手合拢时可以获得最大速度。
最后,我们将我们的结果汇编成一份提案,尽我们所能帮助运动员,我们期待着他们继续取得成功!
模型假设:
为了简化给定的问题,我们对我们的模型做出以下假设:
1、假设人体部分的某种几何近似对模型结果的影响可以忽略不计。
2、假设游泳时惯性阻力和空气阻力可以忽略不计。
3、假设动态阻力在游泳过程中提供完全推进力。
4、假设在游泳过程中身体各部分之间的角度保持不变,并且在一次游泳过程中人体运动的频率不变。
5、仰泳腿的动作可视为与自由泳相同,由于人体关节的限制,手不能达到与自由泳相同的运动幅度。因此,我们参考文献,并考虑由半臂冲程提供的身体前半部分的推进力。
问题重述:
问题背景
游泳是众所周知的一项竞技运动。在游泳项目中,运动员经常被要求使用特定的游泳方式进行比赛,在一定距离内能花最短时间的运动员将获胜。在游泳比赛中,目前常见的游泳方式有四种:爬泳、蛙泳、蝶泳和仰泳,它们都要求不同的动作和标准。在奥运会上,这四种风格都是合理的游泳方式,具有不同的竞技要求。
现在,有必要弄清楚四种方法中哪种最快,哪种游泳方法可以获得最大的推进力。此外,在自由泳项目中,由于没有规定的游泳泳姿,运动员往往选择爬行。那么,在自由泳中,是否有可能进一步提高泳姿,从而达到更快的旅行速度?这是本文要解决的问题。
此外,我们还有光荣的使命。通过数学模型对问题进行分析,提出改进游泳风格的方案,并提出建议,供运动员训练时参考,以达到更好的效果!
我们的工作
通过我们的游泳知识和流体动力学分析,我们开发了几个数学模型,可以说明该主题所需的问题。具体如下:
•通过对人体在四种泳姿中不同运动的几何近似,将手臂和手视为一个统一的圆柱体,腿和脚视为圆柱体,根据流体力学中的流体阻力公式计算四种泳姿的推进力,并根据推进力和阻力公式结合牛顿第二定律求解偏微分方程,得到各泳姿速度与行程时间的关系。这将导致最推进和最快的冲程。
•在上述结论的基础上,我们对爬行动作进行了较为详细的分解,将手臂分别视为上臂、前臂和手掌分别视为两个圆柱体和一个椭圆形圆柱体,设置游泳过程中手臂之间的夹角,并求出解出的方程的极值,得到能使速度最大化的身体角度。
•此外,我们推测手掌的手指张开度也会对有效速度产生影响,为此,我们模拟了与手指张开角度相关的推进力。根据该模型,我们可以得到最合适的角度。
•最后,我们将我们的研究成果汇编成一份详细的方案,供运动员在训练期间参考,希望该方案能帮助他们取得更好的效果。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
function dVb=he(t,Vb,gama,beita)
D1=0.083;
La1=0.34;
D2=0.054;
La2=0.3;
Ah=0.019;
Lh=0.19;
Ka=400;
Kb=31.487;
Kh=900;
f=1.11;
xita=mod(2*pi*f*t,pi);
dVb=((Ka*D1*(4/3*pi^2*f^2*La1^3*sin(gama)^2-2*pi*f*La1^2*Vb*sin(xita)*sin(gama)+
La1*Vb^2*sin(xita)^2)+Ka*D2*(4/3*pi^2*f^2*La2^3*sin(beita)^2+4*pi^2*f^2*La2^2*La1*
sin(beita)*sin(gama)+4*pi^2*f^2*La1^2*La2*sin(gama)^2-2*pi*f*La2^2*Vb*sin(beita)
*sin(xita)-4*pi*f*La1*La2*Vb*sin(gama)*sin(xita)+La2*Vb^2*sin(xita)^2)+Kh*Ah*
(4*pi^2*f^2*(La1*sin(gama)+La2*sin(beita)+Lh*sin(beita)/2)^2-4*pi*f*
(La1*sin(gama)+La2*sin(beita)+Lh*sin(beita)/2)*Vb*sin(xita)+Vb^2*sin(xita)^2 ))
*sin(xita)-sign(Vb)*Kb*Vb^2)/60;
end
S1=zeros(numel(0:pi/2/90:pi),numel(0:pi/2/90:pi));
max_S=0;
max_gama=0;
max_beita=0;
for gama=0:pi/2/90:pi
for beita=0:pi/2/90:pi
[t11,y11]=ode45(@(t,Vb)he(t,Vb,gama,beita),[0,27],0);
plot(t11,y11);
X1=[t11 y11];
S1(round(gama/(pi/2/90)+1),round(beita/(pi/2/90)+1))
=(numel(0:27)-1)/numel(X1(:,1))*sum(X1(:,2));
if(S1>=max_S)
max_S=S1;
max_gama=gama;
max_beita=beita;
end
end
end
max_gama=max_beita/pi*180;
max_beita=max_beita;
gama1=0:pi/2/90:pi;
beita1=0:pi/2/90:pi;
gama1=gama1/pi*180;
beita1=beita1/pi*180;
[gama2,beita2]=meshgrid(0:0.2:180,0:0.2:180);
S11=griddata(gama1,beita1,S1,gama2,beita2)
shading interp
mesh(gama2,beita2,S11)
clc
clear
T_t=10;
%f=1.667
%T=0.6s
T=0.9;
f=1.11;
A1=50.735;
A2=31.487;
A3=25.735;
L1=(533+90)/1000;%
%sign(2*pi*f*L1-y*sin(2*pi*f*t))*
L2=878/1000;
%%
% T_xs0=0;A_xs0=0;
% T_xs1=-0.1;A_xs1=0;
% T_xs2=-0.05;A_xs2=0;
% T_xs3=0.05;A_xs3=0;
% T_xs4=0.1;A_xs4=0;
%%
T_xs0=0;A_xs0=0;
T_xs1=0;A_xs1=0.2;
T_xs2=0;A_xs2=0.1;
T_xs3=0;A_xs3=-0.1;
T_xs4=0;A_xs4=-0.2;
[t0,y0]=ode45(@(t,y)free_Fenxi_fucntion(t,y,T_xs0,A_xs0),[0,T_t],0);
[t1,y1]=ode45(@(t,y)free_Fenxi_fucntion(t,y,T_xs1,A_xs1),[0,T_t],0);
[t2,y2]=ode45(@(t,y)free_Fenxi_fucntion(t,y,T_xs2,A_xs2),[0,T_t],0);
[t3,y3]=ode45(@(t,y)free_Fenxi_fucntion(t,y,T_xs3,A_xs3),[0,T_t],0);
[t4,y4]=ode45(@(t,y)free_Fenxi_fucntion(t,y,T_xs4,A_xs4),[0,T_t],0);
%%
X1=[t0 y0];
S0=(numel(0:T_t)-1)/numel(X1(:,1))*sum(X1(:,2));
S00=zeros(1,numel(t0));
S00(1)=y0(1);
for i0=2:numel(t0)
S00(i0)=S00(i0-1)+(numel(0:T_t)-1)/numel(X1(:,1))*y0(i0);
end
%%
X1=[t1 y1];
S1=(numel(0:T_t)-1)/numel(X1(:,1))*sum(X1(:,2));
S11=zeros(1,numel(t1));
S11(1)=y1(1);
for i11=2:numel(t1)
S11(i11)=S11(i11-1)+(numel(0:T_t)-1)/numel(X1(:,1))*y1(i11);
end
%%
X2=[t2 y2];
S2=(numel(0:T_t)-1)/numel(X2(:,1))*sum(X2(:,2));
S22=zeros(1,numel(t2));
S22(1)=y2(1);
for i22=2:numel(t2)
S22(i22)=S22(i22-1)+(numel(0:T_t)-1)/numel(X2(:,1))*y2(i22);
end
%%
X3=[t3 y3];
S3=(numel(0:T_t)-1)/numel(X3(:,1))*sum(X3(:,2));
S33=zeros(1,numel(t3));
S33(1)=y3(1);
for i33=2:numel(t3)
S33(i33)=S33(i33-1)+(numel(0:T_t)-1)/numel(X3(:,1))*y3(i33);
end
%%
X4=[t4 y4];
S4=(numel(0:T_t)-1)/numel(X4(:,1))*sum(X4(:,2));
S44=zeros(1,numel(t4));
S44(1)=y4(1);
for i44=2:numel(t4)
S44(i44)=S44(i44-1)+(numel(0:T_t)-1)/numel(X4(:,1))*y4(i44);
end
D_fenxi_picture(t0, S00, t1, S11, t2, S22, t3, S33, t4, S44, y0,y1,y2,y3,y4)
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2020年第九届数学建模国际赛小美赛A题自由泳解题全过程文档及程序
2020年第九届数学建模国际赛小美赛 A题 自由泳 原题再现: 在所有常见的游泳泳姿中,哪一种最快?哪个冲程推力最大?在自由泳项目中,游泳者可以选择他们的泳姿,他们通常选择前面的爬行。然而,游泳…...
双端队列和优先级队列
文章目录 前言dequedeque底层设计迭代器设计 priority仿函数数组中的第k个最大元素优先级队列模拟实现pushpop调整仿函数存储自定义类型 前言 今天要介绍比较特殊的结构,双端队列。 还有一个适配器,优先级队列。 deque 栈的默认容器用了一个deque的东西…...

c#读取CSV文件跟Excel导入成DataTble
1.读取CSV文件 /// <summary>/// 读取CSV文件/// </summary>/// <param name"fileName">文件路径</param>public static DataTable ReadCSV(string fileName){DataTable dt new DataTable();FileStream fs new FileStream(fileName, FileM…...

Python编程技巧 – 单字符函数
Python编程技巧 – 单字符函数 Python Programming Skills – Single Character Function By JacksonML 0. 前言 Python有其内建(built-in)的一系列函数,其中,有两个函数为长度为一的字符设计。这样的函数是单字符函数,尽管它们操作的对象…...

xcode-文件
IOSDeviceSupoprt 共享缓存库 当你使用新的 iOS 设备连接到 Xcode 时,Xcode 会自动下载并存储相应版本的设备支持文件。 每个 iOS 版本都有一个对应的设备支持文件集,这些文件包含有关设备架构和操作系统的信息,以便 Xcode 能够正确地调试和…...

云原生之深入解析网络服务Istio、eBPF和RSocket Broker
一、服务治理 ① “服务治理”简介 在微服务时代,一个复杂的应用程序被分解为多个组件化、协作和连接的单元,服务往往会承担越来越多的业务责任,这使得服务治理的难度前所未有,仅仅依靠微服务框架级的治理是不够的,构…...

文件系统和磁盘调度
文件系统 概述 文件系统:一种用于持久性存储的系统抽象 在存储器上:组织、控制、导航、访问和检索数据大多数计算机包含文件系统 文件:文件系统中一个单元的相关数据在操作系统中的抽象 文件系统功能 分配文件磁盘空间 管理文件块管理空…...

C++ stringOJ练习题
目录 把字符串转换成整数 反转字符串 字符串中的第一个唯一字符 字符串最后一个单词的长度 找出字符串中第一个只出现一次的字符 字符串相加 字符串最后一个单词长度 字符串相乘 反转字符串3 反转字符串2 验证回文串 把字符串转换成整数 通过遍历字符串并逐位转换…...
解决问题:ImportError: cannot import name ‘_update_worker_pids‘
在复现一些较早年份文献时,网络架构是较早的Pytorch模型,现阶段的高版本不兼容,所以就得安装比如低版本的torch0.4.0以解决问题。 目录 一、问题1.1 问题分析 二、解决办法2.1 Pytorch安装2.2 torchvision安装2.3 测试是否安装成功 三、总结…...
【面试总结】Java面试题目总结(一)
(以下仅为个人见解,如果有误,欢迎大家批评并指出错误,谢谢大家) 1.项目中的验证码功能是如何实现的? 第一步:在项目的pom.xml文件中导入 EasyCaptcha 的依赖; <dependency>…...
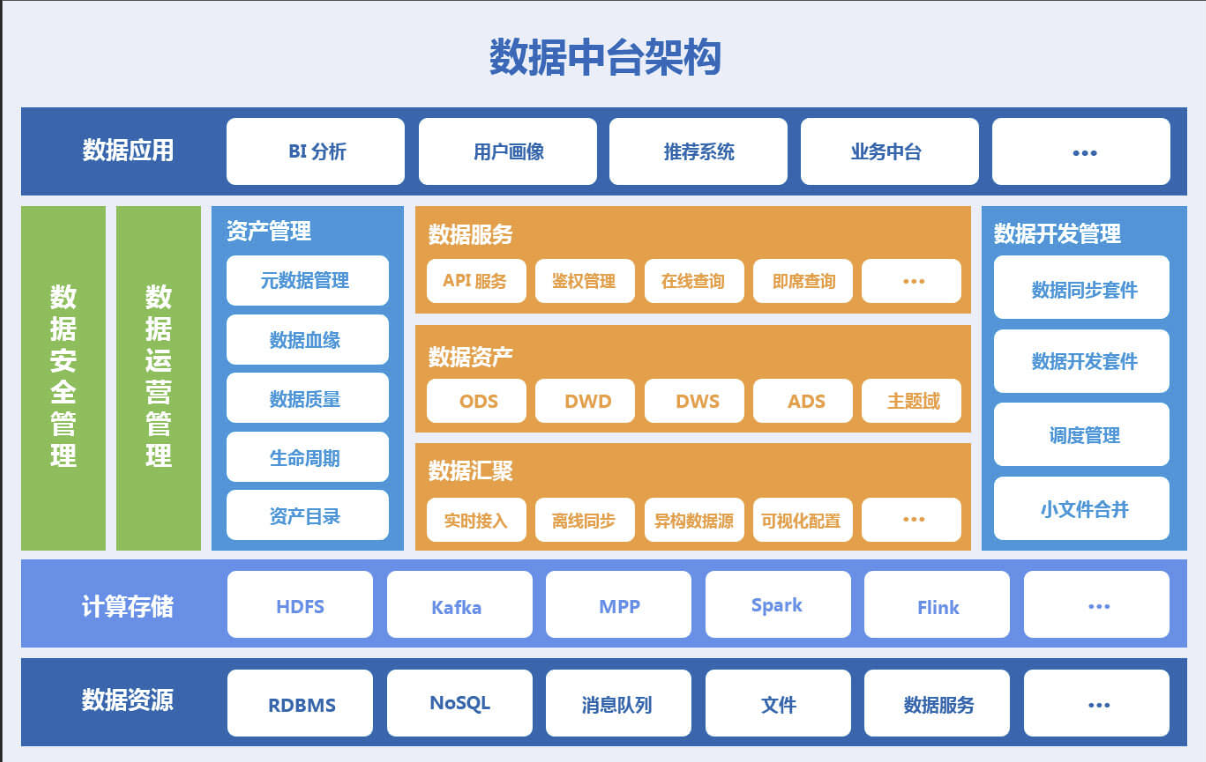
大白话数据中台,何为数据中台
文章目录 一、数据中台二、本质三、构建数据中台的几个方面四、总结 最近一直在研发Ai平台,忙碌非凡。 在之余,有小伙伴质疑数据中台其实就是一个web系统,无法就是添加一些业务逻辑的增删改查。 答曰: 回去好好把科普下什么是数…...
escapeshellarg参数绕过和注入的问题
escapeshellcmd escapeshellcmd(string $command): string command--要转义的命令。 escapeshellcmd() 对字符串中可能会欺骗 shell 命令执行任意命令的字符进行转义。 此函数保证用户输入的数据在传送到 exec() 或 system() 函数,或者 执行操作符 之前进行转义。 …...

CSS——标准流、浮动、Flex布局
1、标准流 标准流也叫文档流,指的是标签在页面中默认的排布规则,例如:块元素独占一行,行内元素可以一行显示多个。 2、浮动 作用:让块元素水平排列 属性名:float 属性值: left:…...
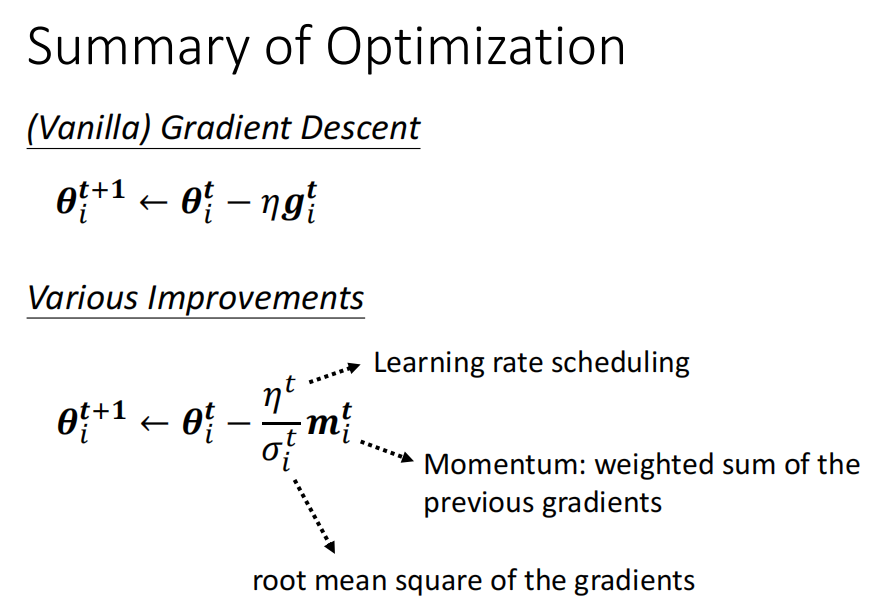
P21 类神经网络训练不起来怎么办- 自动调整学习率 Adapative learning rate
梯度大,学习率减小梯度小,学习率变大adam随时间变化 , decay / warm up 调整学习率方法一 adagrad 学习率除以 梯度的方差 方法二 RMSProp 目前最常用的: Adam: RMSProp Moment Learning rate schedule : decay/ warm up l…...
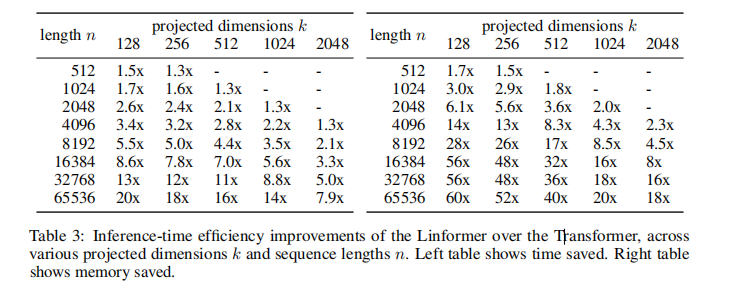
[Linformer]论文实现:Linformer: Self-Attention with Linear Complexity
文章目录 一、完整代码二、论文解读2.1 介绍2.2 Self-Attention is Low Rank2.3 模型架构2.4 结果 三、整体总结 论文:Linformer: Self-Attention with Linear Complexity 作者:Sinong Wang, Belinda Z. Li, Madian Khabsa, Han Fang, Hao Ma 时间&#…...
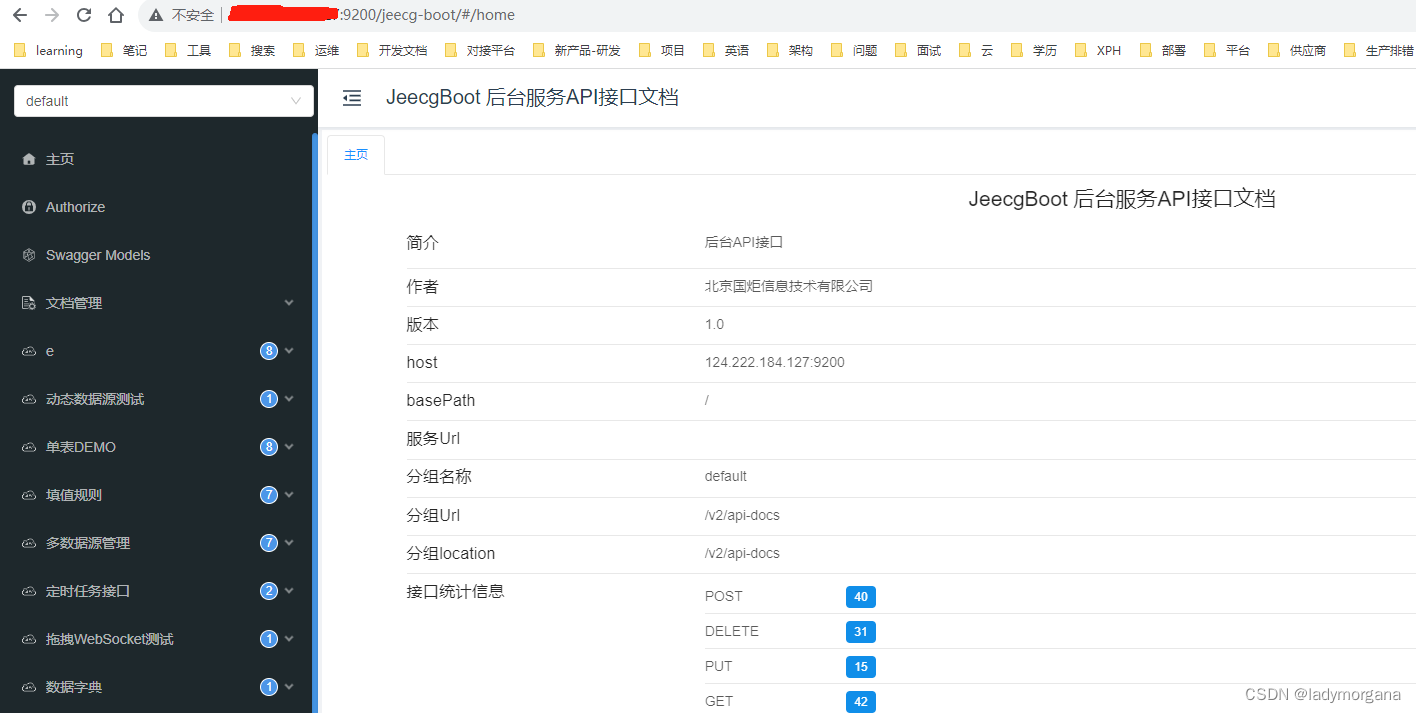
【Jeecg Boot 3 - 第二天】1.1、后端 docker-compose 部署 JEECGBOOT3
一、场景 二、实战 ▶ 2.1 修改配置文件 > 目的一:将 dev 变更为生产环境 prod > 目的二:方便spring项目调用docker同个network下的redis和mysql ▶ 2.2 编写dockerfile ▶ 2.3 编写docker-compose.yaml ▶ 2.4 打…...

Centos单用户模式修改root密码
在CentOS 7的单用户模式下,你可以按照以下步骤修改root用户密码: 启动CentOS 7并进入GRUB菜单。在启动时按下任意键进入GRUB菜单。 在GRUB菜单中,选择要启动的CentOS 7内核版本,并按下e键进行编辑。 找到以 ro 开头的行…...
[Unity]关于Unity接入Appsflyer并且打点支付
首先需要去官方下载Appsflyer的UnityPackage 链接在这afPackage 然后导入 导入完成 引入此段代码 using AppsFlyerSDK; using System.Collections; using System.Collections.Generic; using UnityEngine;public class AppflysManager : MonoBehaviour {public static App…...

AICore 带来了 Android 专属的 AI 能力,它要解决什么?采用什么架构思路?
前言 Google 最近发布的 Gemini 模型在全球引起了巨大反响,其在多模态领域的 Video demo 无比震撼。对于 Android 开发者而言,其中最振奋人心的消息莫过于 Gemini Nano 模型将内置到 Android 系统当中,并开放给开发者使用。 事实上…...
python学习1
大家好,这里是七七,今天开始又新开一个专栏,Python学习。这次思考了些许,准备用例子来学习,而不是只通过一大堆道理和书本来学习了。啊对,这次是从0开始学习,因此大佬不用看本文了,小…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
