C++实现AVL树
目录
一、搜索二叉树
1.1 搜索二叉树概念
二、模拟实现二叉搜索树
2.1 框架
2.2 构造函数
2.2.1 构造函数
2.2.2 拷贝构造
2.2.3 赋值拷贝
2.3 插入函数
2.3.1 insert()
2.3.2 RcInsert() 递归实现
2.4 删除结点函数
2.4.1 Erase()
2.4.2 RcErase()
2.5 中序遍历
2.6 查找函数find()
2.7 析构函数
2.8 测试函数
三、AVL算法实现平衡二叉搜索树
3.1 普通搜索二叉树的性能分析
3.2 AVL树概念与性质
3.3 AVL树结点的定义
3.4 AVL树结点插入
3.5 AVL树旋转算法保持树平衡
3.5.1 新节点插入较高左子树的左侧---左左:右单旋
3.5.2 新节点插入较高右子树的右侧---右右:左单旋
3.5.3 新节点插入较高左子树的右侧---左右:先左单旋再右单旋
3.5.4 新节点插入较高右子树的左侧---右左:先右单旋再左单旋
3.6 判断一个搜索二叉树是否为平衡
3.7 测试AVL树
一、搜索二叉树
1.1 搜索二叉树概念
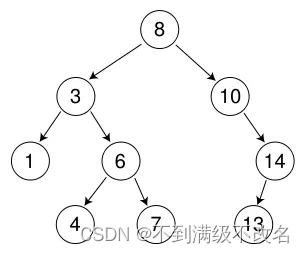
百度:
搜索二叉树或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值 。
二、模拟实现二叉搜索树
2.1 框架
namespace K
{//结点类template <class T>class BSNode{public:BSNode(const T& data = T()):_data(data),_left(nullptr),_right(nullptr){}public:T _data;BSNode<T>* _left;BSNode<T>* _right;};//搜索二叉树template<class T>class BSTree{public:typedef BSNode<T> Node;BSTree();BSTree(const BSTree<T>& t);BSTree<T>& operator=(BSTree<T> tmp);~BSTree();bool insert(const T& x = T());//中序遍历(从小到大)void InOrder();bool find(const T& x);bool Erase(const T& x);//recursive 递归实现bool RcFind(const T& x);bool RcInsert(const T& x);bool RcErase(const T& x);private:Node* root;};
}2.2 构造函数
2.2.1 构造函数
BSTree():root(nullptr)
{}2.2.2 拷贝构造
void copyTree(const Node* r)
{if (r == nullptr)return;insert(r->_data);copyTree(r->_left);copyTree(r->_right);
}BSTree(const BSTree<T>& t):root(nullptr)
{copyTree(t.root);
}2.2.3 赋值拷贝
BSTree<T>& operator=(BSTree<T> tmp)
{swap(root, tmp.root);return *this;
}2.3 插入函数
2.3.1 insert()
bool insert(const T& x = T())
{if (root == nullptr){root = new Node(x);return true;}//root!=nullprtNode* cur = root;Node* prev = nullptr;while (cur){prev = cur;//比根大,往右子树走if (x > cur->_data){cur = cur->_right;}//比根小,往左子树走else if (x < cur->_data){cur = cur->_left;}//相等不符合规则,返回falseelsereturn false;}//链接(比根小,链左边,比根大链右边)cur = new Node(x);if (x > prev->_data) prev->_right = cur;else prev->_left = cur;return true;
}2.3.2 RcInsert() 递归实现
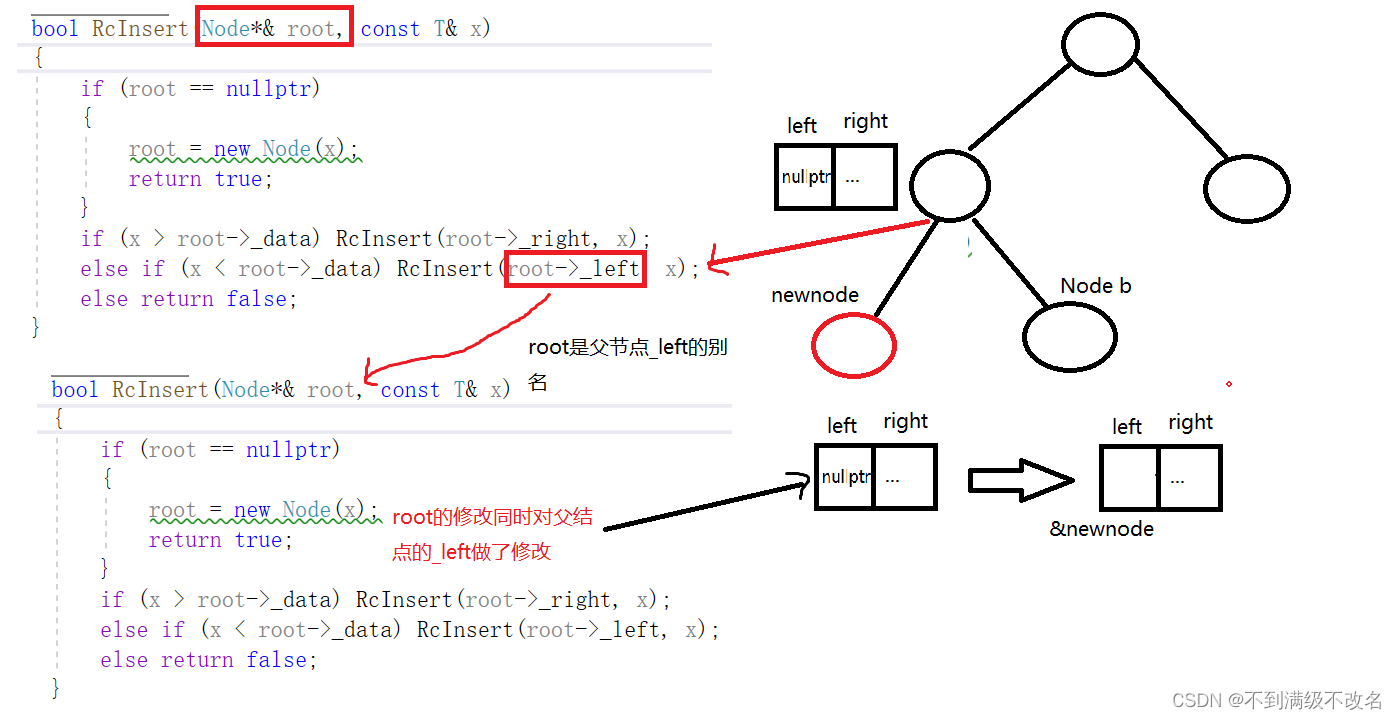
public:
bool RcInsert(const T& x)
{return _RcInsert(root, x);//因为根的私有性,我们用间接调用的方式实现函数功能
}private:
bool _RcInsert(Node*& root, const T& x)
{if (root == nullptr){root = new Node(x);return true;}if (x > root->_data) _RcInsert(root->_right, x);else if (x < root->_data) _RcInsert(root->_left, x);else return false;
}2.4 删除结点函数


2.4.1 Erase()
bool Erase(const T& x)
{if (root == nullptr)return false;Node* cur = root;Node* prev = nullptr;// 找到要删除的结点while (cur){if (x > cur->_data){prev = cur;cur = cur->_right;}else if (x < cur->_data){prev = cur;cur = cur->_left;}else break;}//情况cif (cur->_left == nullptr){if (prev == nullptr){root = cur->_right;}else{if (cur->_data > prev->_data)prev->_right = cur->_right;else prev->_left = cur->_right;}delete cur;}//情况belse if (cur->_right == nullptr){if (prev == nullptr){root = cur->_left;}else{if (cur->_data > prev->_data)prev->_right = cur->_left;else prev->_left = cur->_left;}delete cur;}//情况delse{Node* minRight = cur->_right;prev = cur;while (minRight->_left){prev = minRight;minRight = minRight->_left;}cur->_data = minRight->_data;//千万要记得先将minRight的右结点和其父节点链接在一起if (minRight == prev->_left)prev->_left = minRight->_right;else prev->_right = minRight->_right;delete minRight;}return true;
}2.4.2 RcErase()
public:
bool RcErase(const T& x)
{return _RcErase(root, x);
}
private:
bool _RcErase(Node*& root, const T& x)
{if (root == nullptr)return false;if (x > root->_data) _RcErase(root->_right, x);else if (x < root->_data) _RcErase(root->_left, x);else{Node* tmp = root;if (root->_left == nullptr){root = root->_right;delete tmp;}else if (root->_right == nullptr){Node* tmp = root;root = root->_left;delete tmp;}else{Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}root->_data = minRight->_data;//递归删除minright_RcErase(root->_right, root->_data);}}return true;
}2.5 中序遍历
public:
void InOrder()
{_InOrder(root);cout << endl;
}
private:
void _InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_data << ' ';_InOrder(root->_right);
}2.6 查找函数find()
bool find(const T& x)
{if (root == nullptr)return false;Node* cur = root;while (cur){if (x > cur->_data)cur = cur->_right;else if (x < cur->_data)cur = cur->_left;else return true;}return false;
}2.7 析构函数
public:
~BSTree()
{Destroy(root);
}
private:
void Destroy(Node* root)
{if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;
}2.8 测试函数
void TestBSTree1()
{int arr[] = { 7,3,5,2,1,9,4,8,6 };K::BSTree<int> tree;for (auto e : arr){tree.insert(e);}tree.InOrder();for (int i = 1;i <= 9;i++){tree.Erase(i);tree.InOrder();}
}void TestBSTree2()
{int arr[] = { 7,3,5,2,1,9,4,8,6 };K::BSTree<int> tree1;for (auto e : arr){tree1.RcInsert(e);}tree1.InOrder();K::BSTree<int> tree2;tree2 = tree1;tree2.InOrder();
}三、AVL算法实现平衡二叉搜索树
3.1 普通搜索二叉树的性能分析

最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:logN
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:O(N)
3.2 AVL树概念与性质
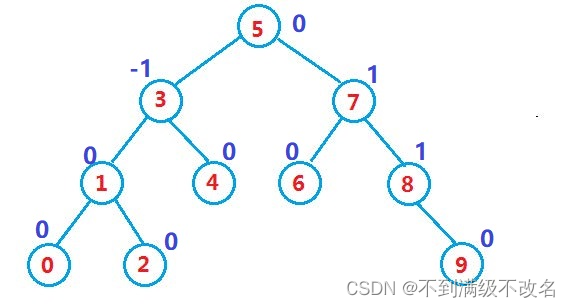
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。
因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
性质:
1.它的左右子树都是AVL树
2.左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1) 高度差=右树高 - 左树高3.AVL树的查找效率为O(logN)
3.3 AVL树结点的定义
template <class T>
struct AVLTreeNode
{
public:AVLTreeNode(const T& data):_data(data),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}AVLTreeNode<T>* _left;AVLTreeNode<T>* _right;AVLTreeNode<T>* _parent;T _data;int _bf;//树的平衡因子
};3.4 AVL树结点插入
bool insert(const T& data)
{if (_root == nullptr){_root = new Node(data);return true;}//找到插入位置Node* cur = _root;Node* parent = nullptr;while (cur){parent = cur;if (data > cur->_data)cur = cur->_right;else if (data < cur->_data)cur = cur->_left;elsereturn false;}//插入新节点并建立链接cur = new Node(data);cur->_parent = parent;if (cur->_data > parent->_data){parent->_right = cur;}else{parent->_left = cur;}//判断平衡因子while (parent){if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0)break;else if (parent->_bf == -1 || parent->_bf == 1){cur = parent;parent = parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){//右高 右右if (parent->_bf == 2 && cur->_bf == 1)RotateL(parent);//左高 左左else if (parent->_bf == -2 && cur->_bf == -1)RotateR(parent);//右高 右左else if (parent->_bf == 2 && cur->_bf == -1)RotateRL(cur);//左高 左右else if (parent->_bf == -2 && cur->_bf == 1)RotateLR(cur);//任何其他情况都直接报错else assert(false);break;}else{assert(false);}}return true;
}3.5 AVL树旋转算法保持树平衡
3.5.1 新节点插入较高左子树的左侧---左左:右单旋
情况一:左边高且插入结点在父节点左边!
以30结点为轴,将30的右结点与父节点链接,然后将60做30的右结点,这样就可以使树保持为平衡搜索树!

void RotateR(Node* parent)
{Node* SubL = parent->_left;//父节点的左孩子Node* SubLR = SubL->_right;//左孩子的右孩子parent->_left = SubLR;//将左孩子的右孩子与父节点的左链接if (SubLR) SubLR->_parent = parent;//右孩子不为空,则找父亲//下面准备更新SubL为父节点,记录祖父节点Node* gparent = parent->_parent;//更新的节点是根节点,则直接改变rootif (parent == _root){_root = SubL;SubL->_parent = nullptr;}else {//判断父节点与祖父节点的关系if (parent == gparent->_left)gparent->_left = SubL;else gparent->_right = SubL;//与祖父节点链接SubL->_parent = parent->_parent;}//与原父节点链接,其链接在新父节点右SubL->_right = parent;parent->_parent = SubL;//更新平衡因子parent->_bf = SubL->_bf = 0;
}3.5.2 新节点插入较高右子树的右侧---右右:左单旋

情况二:右边高且插入结点在父节点的右边
以60为轴,将60的左结点与父节点30的右链接,将父节点30与60的左链接!
void RotateL(Node* parent)
{Node* SubR = parent->_right;Node* SubRL = SubR->_left;parent->_right = SubRL;if (SubRL) SubRL->_parent = parent;Node* gparent = parent->_parent;if (parent == _root){_root = SubR;SubR->_parent = nullptr;}else {if (parent == gparent->_left)gparent->_left = SubR;else gparent->_right = SubR;SubR->_parent = gparent;}SubR->_left = parent;parent->_parent = SubR;parent->_bf = SubR->_bf = 0;
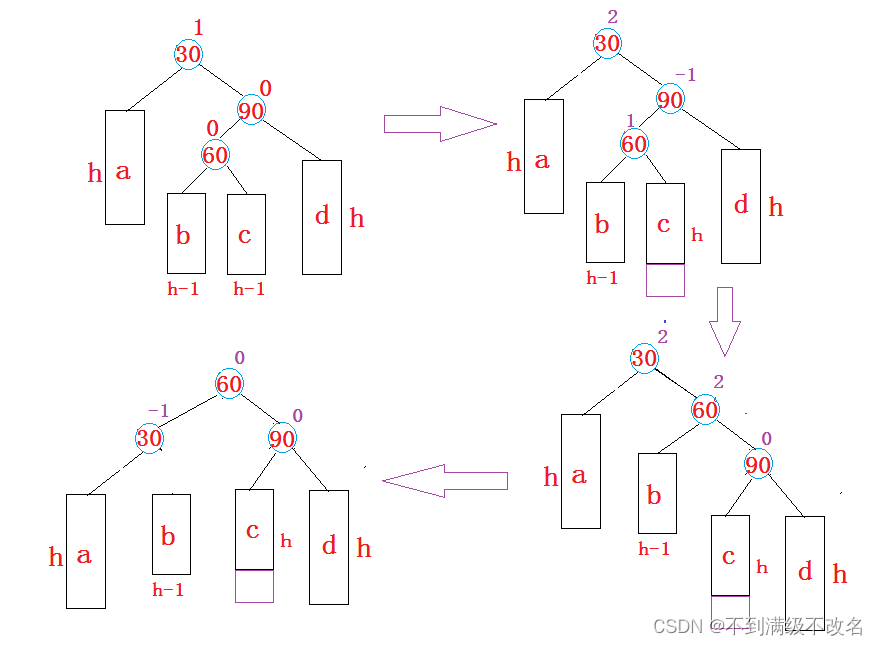
}3.5.3 新节点插入较高左子树的右侧---左右:先左单旋再右单旋
先以60为轴进行左旋,然后以60为轴进行右旋

这里插入新节点后60节点的平衡因子对最后的的30,90平衡因子右影响!
如果60的平衡因子是-1,最后90的平衡因子就是1,30的平衡因子是0。
如果60的平衡因子是1,最后90的平衡因子就是0,30的平衡因子是-1。
如果60的平衡因子是0.最后30,90的平衡因子都是0。
void RotateLR(Node* parent) //parent --> 30节点
{Node* SubR = parent->_right;int bf = SubR->_bf; //记录插入新节点后的60的平衡因子Node* gparent = parent->_parent; //gparent --> 90节点RotateL(parent); //30以60为轴左旋RotateR(gparent); //90以60为轴右旋if (bf == 1){SubR->_bf = 0;parent->_bf = 0;gparent->_bf = -1;}else if (bf == -1){SubR->_bf = 0;parent->_bf = 0;gparent->_bf = 1;}else {SubR->_bf = parent->_bf = gparent->_bf = 0;}
}3.5.4 新节点插入较高右子树的左侧---右左:先右单旋再左单旋
先以60为轴进行右旋,然后以60为轴进行左旋!
同样我们30,90最后平衡因子的更新需要判断60的平衡因子!
void RotateRL(Node* parent)
{Node* SubL = parent->_left;int bf = SubL->_bf;Node* gparent = parent->_parent;RotateR(parent);RotateL(gparent);if (bf == 1){SubL->_bf = 0;parent->_bf = -1;gparent->_bf = 0;}else if (bf == -1){SubL->_bf = 0;parent->_bf = 0;gparent->_bf = 1;}else {SubL->_bf = parent->_bf = gparent->_bf = 0;}
}3.6 判断一个搜索二叉树是否为平衡
//深层遍历,计算每个节点的高度
int TreeHeight(Node* root)
{if (root == nullptr)return 0;int Left_height = TreeHeight(root->_left);int Right_height = TreeHeight(root->_right);//返回左右子树的最大高度+ 1(自己本身) ==此节点的高度return Left_height > Right_height ? Left_height + 1 : Right_height + 1;
}
bool IsBalanceTree(Node* root)
{if (root == nullptr)return true;int Left_height = TreeHeight(root->_left);int Right_height = TreeHeight(root->_right);//判断 1.此时高度下是否满足平衡 2.左子树是否满足 3.右子树是否满足return abs(Left_height - Right_height) <= 1 && IsBalanceTree(root->_left) && IsBalanceTree(root->_right);
}3.7 测试AVL树
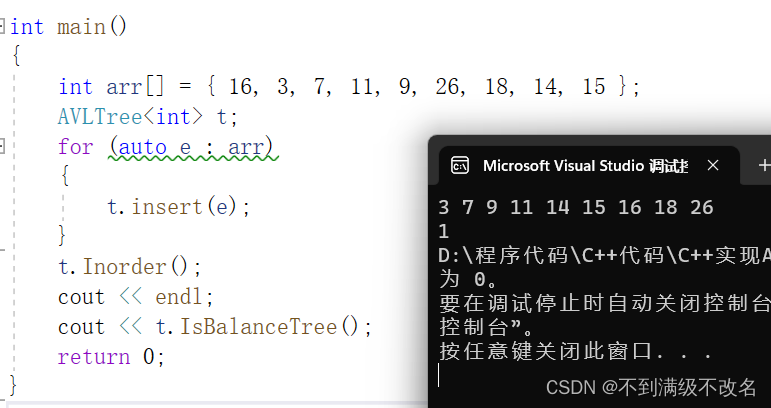
相关文章:

C++实现AVL树
目录 一、搜索二叉树 1.1 搜索二叉树概念 二、模拟实现二叉搜索树 2.1 框架 2.2 构造函数 2.2.1 构造函数 2.2.2 拷贝构造 2.2.3 赋值拷贝 2.3 插入函数 2.3.1 insert() 2.3.2 RcInsert() 递归实现 2.4 删除结点函数 2.4.1 Erase() 2.4.2 RcErase() 2.5 中序遍历…...

高并发语言erlang编程初步
初步 下载安装与初步使用 下载并安装,然后开始菜单中有对应的图标,打开就能进入erlang的命令行。当然也可以将其安装路径的bin文件夹加入环境变量,然后就可以在命令行中输入erl进入erlang了。 在erlang语言中,语句结束需要用.标…...

springboot 问题记录
部署到Tomcat中的时候,找不到需要部署的项目; project facets severt-name severt-class安装lombok.jar eclipse添加lombok插件后闪退打不开Clean 项目,project clean clean的作用检查插件部署项目Springboot修改端口号:applica…...
)
【PAT甲级题解记录】1034 Head of a Gang (30 分)
【PAT甲级题解记录】1034 Head of a Gang (30 分) 前言 Problem:1034 Head of a Gang (30 分) Tags:图的遍历 连通分量统计 DFS Difficulty:剧情模式 想流点汗 想流点血 死而无憾 Address:1034 Head of a Gang (30 分) 问题描述 …...

Python搭建一个steam钓鱼网站,只要免费领游戏,一钓一个准
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 我们日常上网的时候,总是会碰到一些盗号的网站,或者是别人发一些链接给你, 里面的内容是一些可以免费购物网站的优惠券、游戏官网上可以免费领取皮肤、打折的游戏。 这些盗号网站统一的目…...
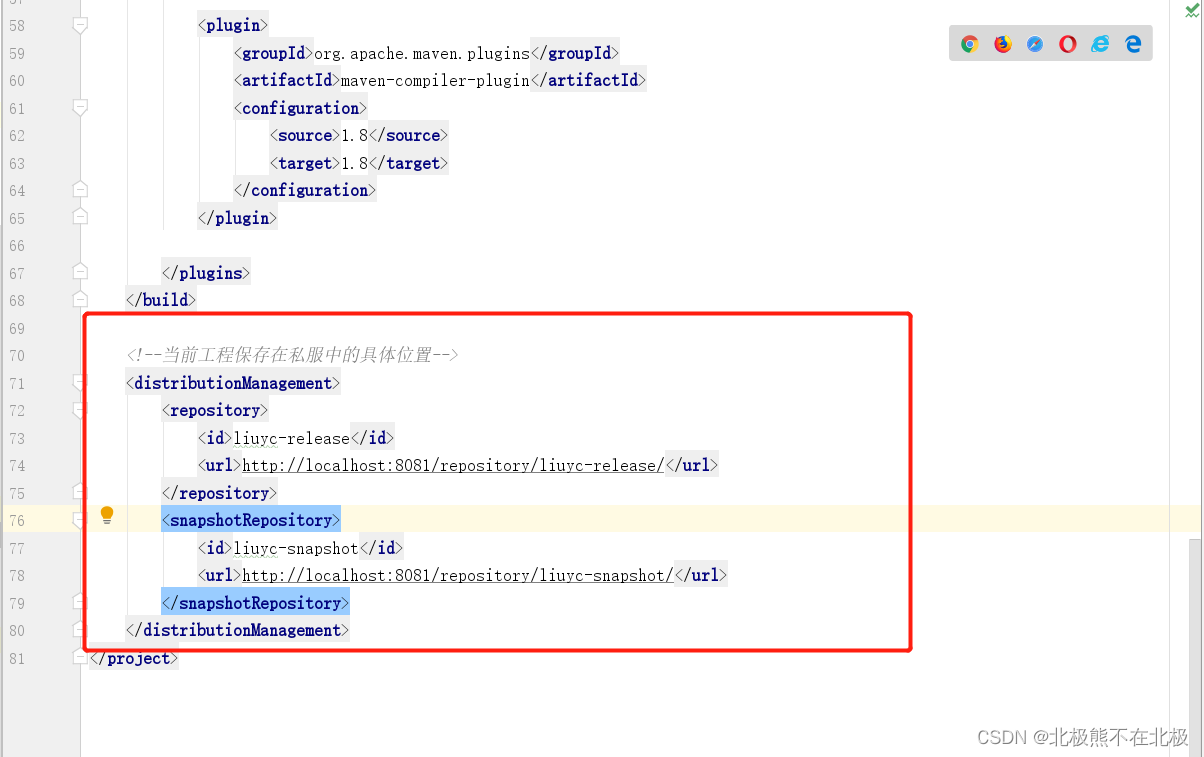
maven 私服nexus安装与使用
一、下载nexus Sonatype公司的一款maven私服产品 1、官网下载地址:https://help.sonatype.com/repomanager3/product-information/download 2、csdn下载地址:https://download.csdn.net/download/u010197591/87522994 二、安装与配置 1、下载后解压如…...
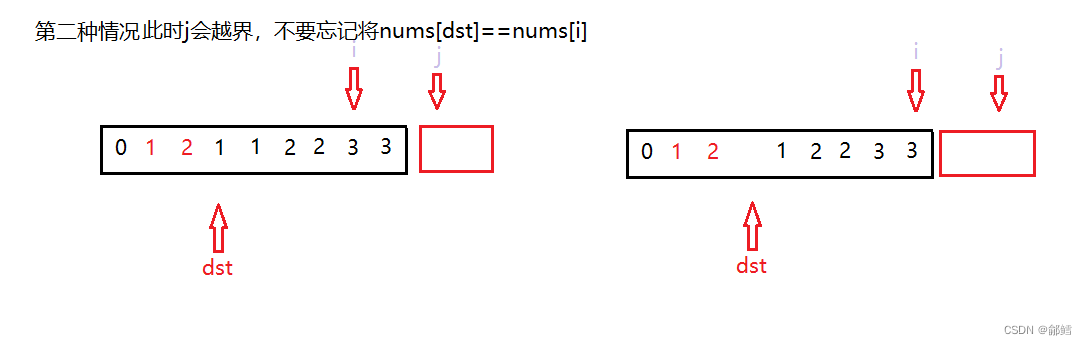
详解数据结构中的顺序表的手动实现,顺序表功能接口【数据结构】
文章目录线性表顺序表接口实现尾插尾删头插头删指定位置插入指定位置删除练习线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序表、链表、栈、队列…...

【二】kubernetes操作
k8s卸载重置 名词解释 1、Namespace:名称用来隔离资源,不隔离网络 创建名称空间 一、命名空间namesapce 方式一:命令行创建 kubectl create ns hello删除名称空间 kubectl delete ns hello查询指定的名称空间 kubectl get pod -n kube-s…...
?)
如何在 C++ 中调用 python 解析器来执行 python 代码(五)?
本节研究如何对 import 做白名单 目录 如何在 C 中调用 python 解析器来执行 python 代码(一)?如何在 C 中调用 python 解析器来执行 python 代码(二)?如何在 C 中调用 python 解析器来执行 python 代码&…...
八 SpringMVC【拦截器】登录验证
目录🚩一 SpringMVC拦截器✅ 1.配置文件✅2.登录验证代码(HandlerInterceptor)✅3.继承HandlerInterceptorAdapter(不建议使用)✅4.登录页面jsp✅5.主页面(操作页面)✅6.crud用户在访问页面时 只…...
PhotoShop基础使用
49:图片分类 1:像素图 特点:放大后可见,右一个个色块(像素)组合而成。 优点:容量小,纯天然 JPG、JPEG、png、GIF 2:矢量图 面向对象图像 绘图图像 特点:不…...

借助阿里云 AHPA,苏打智能轻松实现降本增效
作者:元毅 “高猛科技已在几个主要服务 ACK 集群上启用了 AHPA。相比于 HPA 的方案,AHPA 的主动预测模式额外降低了 12% 的资源成本。同时 AHPA 能够提前资源预热、自动容量规划,能够很好的应对突发流量。” ——赵劲松 (高猛科技高级后台工…...

美团2面:如何保障 MySQL 和 Redis 数据一致性?这样答,让面试官爱到 死去活来
美团2面:如何保障 MySQL 和 Redis 的数据一致性? 说在前面 在尼恩的(50)读者社群中,经常遇到一个 非常、非常高频的一个面试题,但是很不好回答,类似如下: 如何保障 MySQL 和 Redis…...

react hooks学习记录
react hook学习记录1.什么是hooks2.State Hook3.Effect Hook4.Ref Hook1.什么是hooks (1). Hook是React 16.8.0版本增加的新特性/新语法 (2). 可以让你在函数组件中使用 state 以及其他的 React 特性 貌似现在更多的也是使用函数式组件的了,重要 2.State Hook imp…...

创新型中小企业认定评定标准
一、公告条件评价得分达到 60 分以上(其中创新能力指标得分不低于 20 分、成长性指标及专业化指标得分均不低于 15 分),或满足下列条件之一:(一)近三年内获得过国家级、省级科技奖励。(二&#…...

记录一次nginx转发代理skywalking白屏 以及nginx鉴权配置
上nginx代码 #user nobody; worker_processes 1; #error_log logs/error.log; #error_log logs/error.log notice; #error_log logs/error.log info; #pid logs/nginx.pid; events { worker_connections 1024; } http { include mime.types; …...

如何使用FarsightAD在活动目录域中检测攻击者部署的持久化机制
关于FarsightAD FarsightAD是一款功能强大的PowerShell脚本,该工具可以帮助广大研究人员在活动目录域遭受到渗透攻击之后,检测到由攻击者部署的持久化机制。 该脚本能够生成并导出各种对象及其属性的CSV/JSON文件,并附带从元数据副本中获取…...
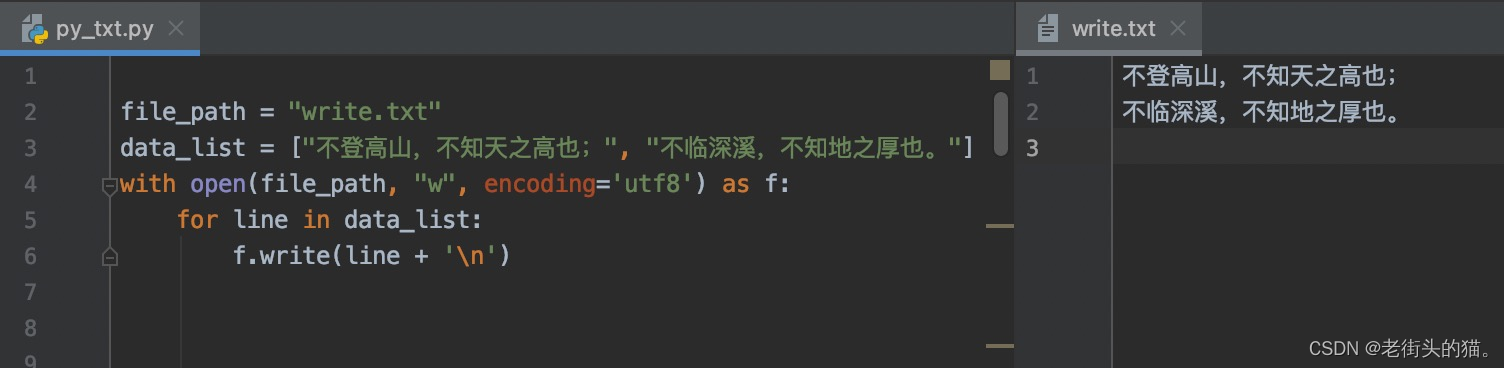
Python - 操作txt文件
文章目录打开txt文件读取txt文件写入txt文件删除txt文件打开txt文件 open(file, moder, bufferingNone, encodingNone, errorsNone, newlineNone, closefdTrue)函数用来打开txt文件。 #方法1,这种方式使用后需要关闭文件 f open("data.txt","r&qu…...

老杜MySQL入门基础 1
1 数据库:DataBase(存储数据的仓库) 2 数据库管理系统:DataBaseManagementSystem(DBMS)(管理数据库中的数据的) DBMS可以对数据库中的数据进行增删改查常见的数据库管理系统:MySQL、Oracle、SQLserver 3 SQL:结构化查询语言 编…...

Vue中splice的使用
splice(index,len,[item])它也可以用来替换/删除/添加数组内某一个或者几个值(该方法会改变原始数组) index:数组开始下标 len: 替换/删除的长度 item:替换的值,删除操作的话 item为空 删除: //删除起始下标为1&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
