当前位置： 首页 > news >正文

软件设计师——信息安全（二）

news 2026/2/11 4:23:54

📑前言

本文主要是【信息安全】——软件设计师——信息安全的文章，如果有什么需要改进的地方还请大佬指出⛺️

🎬作者简介：大家好，我是听风与他🥇
☁️博客首页：CSDN主页听风与他
🌄每日一句：狠狠沉淀，顶峰相见

目录

    • 📑前言
    • 6.SSL加密的网页所采用的协议是（ ）
    • 7.通常利用（ ）技术检测远程主机状态。
    • 8.计算机病毒的特征不包括（ ）。
    • 9.MD5是（ ）算法
    • 10.使用Web方式收发电子邮件时（ ）
    • 📑文章末尾

6.SSL加密的网页所采用的协议是（ ）

6.传输经过SSL加密的网页所采用的协议是（ ）。

  • (A) HTTP
  • (B) HTTPS
  • © S-HTTP
  • (D) HTTP-S

答案与解析

  • 试题难度：容易
  • 知识点：信息安全>网络安全协议
  • 试题答案：[[B]]
  • 试题解析：HTTPS（全称：Hyper Text Transfer Protocol over Secure Socket Layer），是以安全为目标的HTTP通道，简单讲是HTTP的安全版。即HTTP下加入SSL层，HTTPS的安全基础是SSL，因此加密的详细内容就需要SSL。

7.通常利用（ ）技术检测远程主机状态。

7.为了攻击远程主机，通常利用（ ）技术检测远程主机状态。

  • (A) 病毒查杀
  • (B) 端口扫描
  • © QQ聊天
  • (D) 身份认证

答案与解析

  • 试题难度：容易
  • 知识点：信息安全>网络攻击
  • 试题答案：[[‘B’]]
  • 试题解析：端口扫描器通过选用远程 TCP/IP不同的端口的服务，并记录目标给予的回答，通过这种方法，可以搜集到很多关于目标主机的各种有用的信息。

8.计算机病毒的特征不包括（ ）。

  • (A) 传染性
  • (B) 触发性
  • © 隐蔽性
  • (D) 自毁性

答案与解析

  • 试题难度：容易
  • 知识点：信息安全>计算机病毒与木马
  • 试题答案：[[D]]
  • 试题解析：《软件设计师教程（第5版）》P566页：计算机病毒具有隐蔽性、传染性、潜伏性、触发性和破坏性等特定。因此本题选择D选项，自毁性不属于计算机病毒的特征。

9.MD5是（ ）算法

9.MD5是（ ）算法，对任意长度的输入计算得到的结果长度为（ ）位。

  • (A) 路由选择

  • (B) 摘要

  • © 共享密钥

  • (D) 公开密钥

  • (A) 56

  • (B) 128

  • © 140

  • (D) 160

答案与解析

  • 试题难度：一般
  • 知识点：信息安全>信息摘要与数字签名
  • 试题答案：[[B],[B]]
  • 试题解析：《软件设计师教程（第5版）》P45页：MD5是一种摘要算法，经过一系列处理后，算法的输出由四个32位分组组成，将这四个32位分组级联后将生成一个128位散列值。

10.使用Web方式收发电子邮件时（ ）

10.使用Web方式收发电子邮件时，以下描述错误的是（ ）。

  • (A) 无须设置简单邮件传输协议
  • (B) 可以不设置账号密码登录
  • © 邮件可以插入多个附件
  • (D) 未发送邮件可以保存到草稿箱

答案与解析

  • 试题难度：一般
  • 知识点：计算机网络>协议应用提升
  • 试题答案：[[‘B’]]
  • 试题解析：使用WEB方式收发电子邮件时必须设置账号密码登录。

📑文章末尾

在这里插入图片描述

相关文章：

软件设计师——信息安全（二）

📑前言 本文主要是【信息安全】——软件设计师——信息安全的文章，如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介：大家好，我是听风与他🥇 ☁️博客首页：CSDN主页听风与他 &#x1f304…...

编程日记 2023/12/15 23:30:05

Unity中实现ShaderToy卡通火（原理实现篇）

文章目录 前言一、我们在片元着色器中，实现卡通火的大体框架1、使用 noise 和 _CUTOFF 判断作为显示火焰的区域2、_CUTOFF ： 用于裁剪噪波范围的三角形3、noise getNoise(uv, t); : 噪波函数 二、顺着大体框架依次解析具体实现的功能1、 uv.x * 4.0; : …...

编程日记 2023/12/15 23:29:04

引迈信息-JNPF平台怎么样？值得入手吗？

目录 1.前言 2.引迈低代码怎么样？ 3.平台亮点展示 4.引迈产品特点 5.引迈产品技术栈： 1.前言 低代码是近几年比较火的一种应用程序快速开发方式，它能帮助用户在开发软件的过程中大幅减少手工编码量，并通过可视化组件加速应用…...

编程日记 2023/12/15 23:28:03

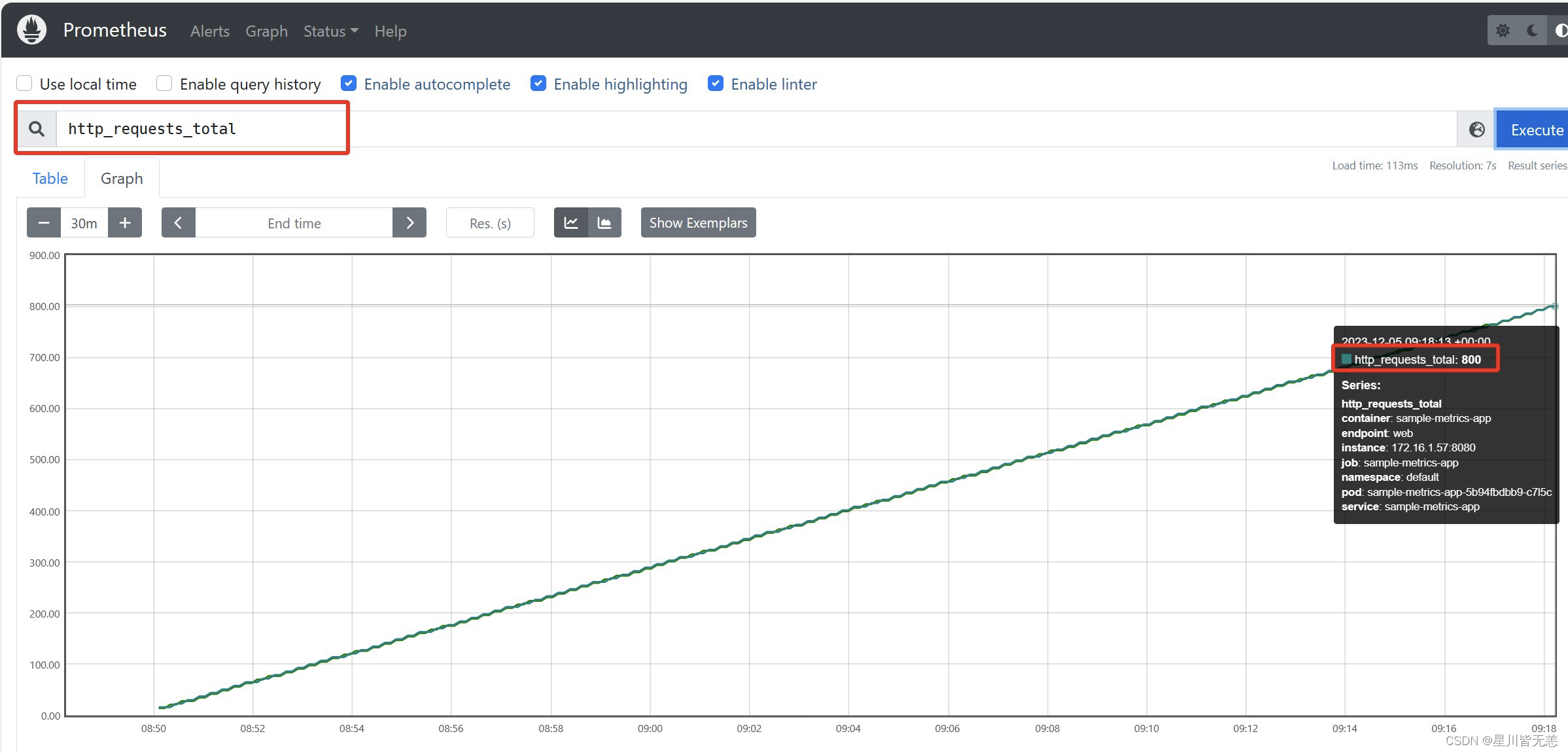
大数据云计算——使用Prometheus-Operator进行K8s集群监控

大数据云计算——使用Prometheus-Operator进行K8s集群监控 一、 背景 在非operator配置的普罗中我们监控k8s集群都是通过配置configmap进行服务发现和指标拉取。切换到prometheus-operator难免会有些使用问题。不少用户已经习惯底层配置自动发现的方式。当过渡到servicemonit…...

编程日记 2023/12/15 23:22:59

[蓝桥杯刷题]合并区间、最长不连续子序列、最长不重复数组长度

前言 ⭐Hello!这里是欧_aita的博客。 ⭐今日语录: 成功的关键在于对目标的持久追求。 ⭐个人主页：欧_aita ψ(._. )>⭐个人专栏： 数据结构与算法 数据库 文章目录 前言合并区间问题📕现实应用大致思路代码实现代码讲解 最长不连续子序列&a…...

编程日记 2023/12/15 23:21:58

Hazel引擎学习（十二）

我自己维护引擎的github地址在这里，里面加了不少注释，有需要的可以看看 参考视频链接在这里 这是这个系列的最后一篇文章，Cherno也基本停止了Games Engine视频的更新，感觉也差不多了，后续可以基于此项目开发自己想要…...

编程日记 2023/12/15 23:19:57

中文字符串逆序输出

今天碰到这个题，让我逆序输出中文字符串，可给我烦死了，之前没有遇到过，也是查了资料才知道，让我太汗颜了。 英文字符串逆序输出很容易，开辟一块空间用来存放逆序后的字符串，从后往前遍历原字符串…...

编程日记 2023/12/15 23:18:56

MySQL BinLog 数据还原恢复

博文目录 文章目录 查看状态查看 binlog 开关及存储路径查看 binlog 配置 如 存储格式 binlog_format查看当前还存在的日志查看当前正在使用的日志 切换日志确定日志确定日志文件日志格式改写日志简要说明确定日志位置以事件为单位查看日志分析日志 还原数据 查看状态 查看 b…...

编程日记 2023/12/15 23:17:55

理想汽车校招内推--大量hc等你来

投递链接: https://li.jobs.feishu.cn/s/i8BLJE1j 欢迎大家投递...

编程日记 2023/12/15 23:11:50

RabbitMQ死信队列详解

什么是死信队列 由于特定的**原因导致 Queue 中的某些消息无法被消费，**这类消费异常的数据将会保存在死信队列中防止消息丢失，例如用户在商城下单成功并点击支付后，在指定时间未支付时的订单自动失效死信队列只不过是绑定在死信交换机上的队…...

编程日记 2023/12/15 23:10:49

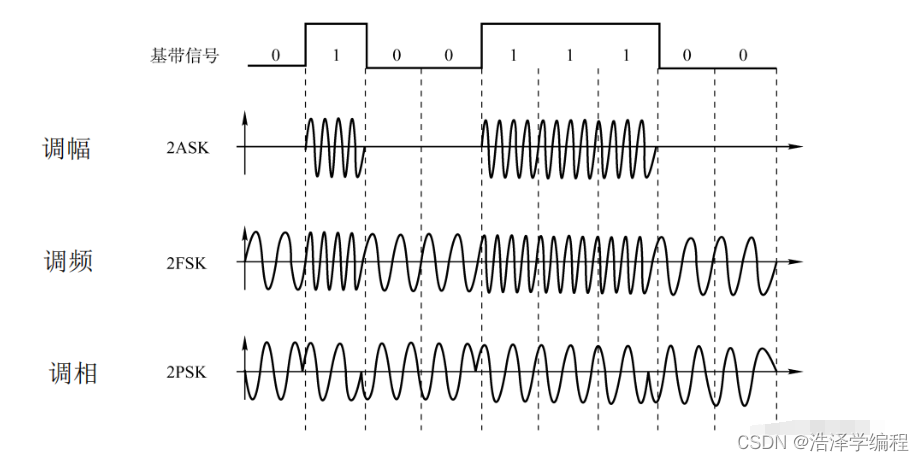
计算机网络：物理层（编码与调制）

今天又学会了一个知识，加油！ 目录 一、基带信号与宽带信号 1、基带信号 2、宽带信号 3、选择 4、关系 二、数字数据编码为数字信号 1、非归零编码【NRZ】 2、曼彻斯特编码 3、差分曼彻斯特编码 4、归零编码【RZ】 5、反向不归零编码【NRZI】 …...

编程日记 2023/12/15 23:09:48

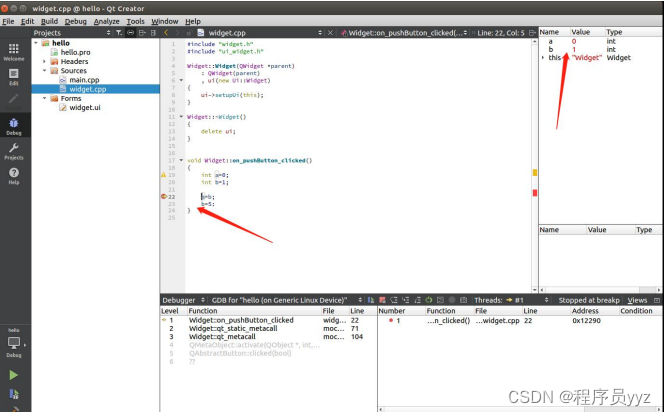
嵌入式开发板qt gdb调试

1） 启动 gdbserver ssh 或者 telnet 登陆扬创平板 192.168.0.253， 进入命令行执行如下： chmod 777 /home/HelloWorld （2） 打 开 QTcreator->Debug->StartDebugging->Attach to Running Debug Server 进行…...

编程日记 2023/12/15 23:06:46

基于python实现原神那维莱特开转脚本

相信不少原友都抽取了枫丹大C那维莱特，其强力的输出让不少玩家爱不释手。由于其转的越快，越不容易丢伤害的特点，很多原友在开转时容易汗流浃背，所以特意用python写了一个自动转圈脚本，当按住鼠标侧键时，即可…...

编程日记 2023/12/15 23:05:45

C# 实现Lru缓存

C# 实现Lru缓存 LRU 算法全称是最近最少使用算法（Least Recently Use），是一种简单的缓存策略。 通常用在对象池等需要频繁获取但是又需要释放不用的地方。 代码实现的基本原理就是使用链表，当某个元素被访问时（Get或…...

编程日记 2023/12/15 23:04:44

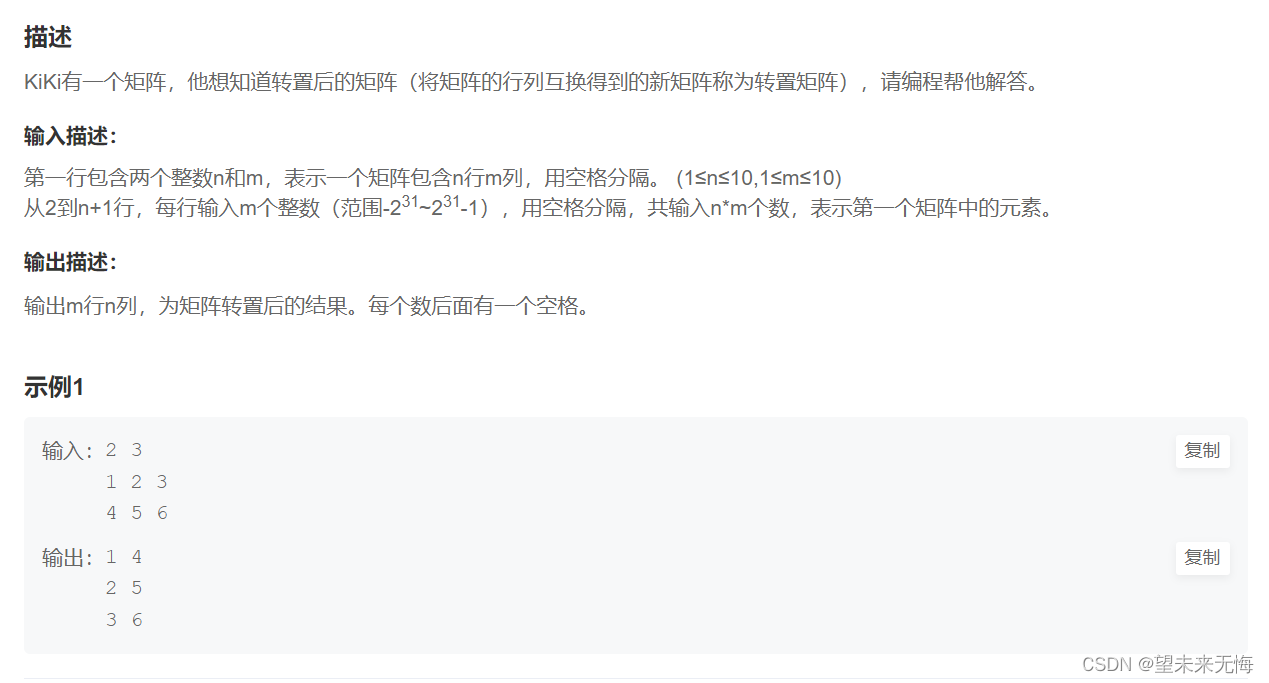
牛客网BC107矩阵转置

答案&#xff1a; #include <stdio.h> int main() {int n0, m0,i0,j0,a0,b0;int arr1[10][10]{0},arr2[10][10]{0}; //第一个数组用来储存原矩阵&#xff0c;第二个数组用来储存转置矩阵scanf("%d%d",&n,&m); if((n>1&&n<10)&&am…...

编程日记 2023/12/15 23:03:44

协作办公原来如此简单？详解 ONLYOFFICE 协作空间 2.0 更新

协作办公原来如此简单&#xff1f;详解 ONLYOFFICE 协作空间 2.0 更新 上周&#xff0c;ONLYOFFICE 的协作空间推出升级版 2.0 版本了&#xff1a; ONLYOFFICE 协作空间 2.0 现已发布&#xff1a;新增公共房间、插件、重新分配数据、RTL 界面等功能 ONLYOFFICE 协作空间是去…...

编程日记 2023/12/15 23:01:42

2023年国赛高教杯数学建模A题定日镜场的优化设计解题全过程文档及程序

2023年国赛高教杯数学建模 A题 定日镜场的优化设计 原题再现 构建以新能源为主体的新型电力系统&#xff0c;是我国实现“碳达峰”“碳中和”目标的一项重要措施。塔式太阳能光热发电是一种低碳环保的新型清洁能源技术[1]。   定日镜是塔式太阳能光热发电站&#xff08;以下…...

编程日记 2023/12/15 23:00:41

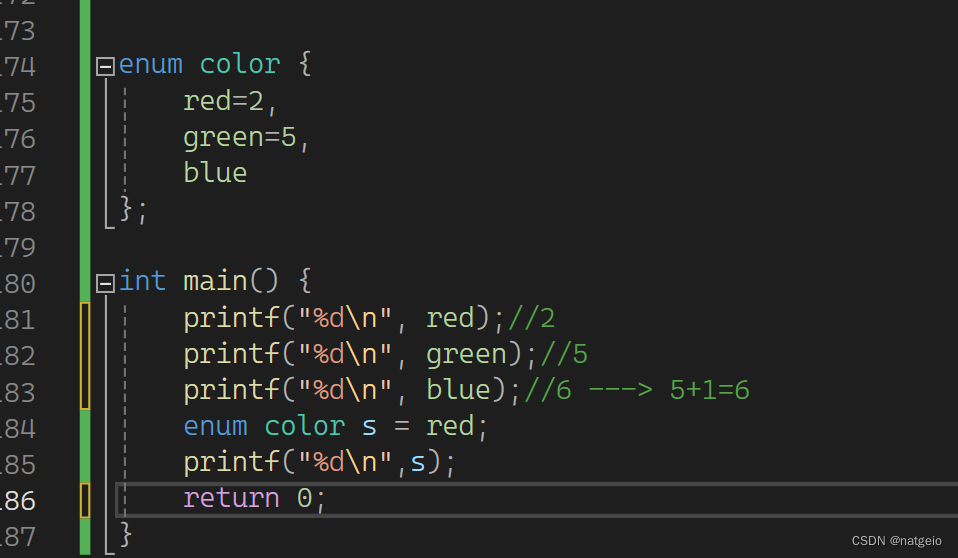
c/c++ 结构体、联合体、枚举

结构体 结构体内存对齐规则&#xff1a; 1、结构体的第一个成员对齐到结构体变量起始位置偏移量为0的地址处 2、其他成员变量要对齐到某个数字&#xff08;对齐数&#xff09;的整数倍的地址处。 对齐数&#xff1a;编译器默认的一个对齐数与该成员变量大小的较小值。 vs 中…...

编程日记 2023/12/15 22:55:37

stl模板库成员函数重载类型混肴编译不通过解决方法

stl模板库成员函数重载类型混肴编译不通过解决方法 这种方式编译不通过IsArithmetic和HasMemberList编译器存在混肴 template <typename T, typename Enable std::enable_if<IsArithmetic<T>::value>::type >static void DumpWrapper(T* filed, std::strin…...

编程日记 2023/12/15 22:51:34

MySQL——表的约束

目录 一.表的约束 二.空属性 ​编辑三.默认值 四.列描述 五.主键 1.主键 2.符合主键 六.自增长 七.唯一键 八.外键 一.表的约束 真正约束字段的是数据类型&#xff0c;但是数据类型约束很单一&#xff0c;需要有一些额外的约束&#xff0c;更好的保证数据的合法性&…...

编程日记 2023/12/15 22:50:34

IDEA运行Tomcat出现乱码问题解决汇总

最近正值期末周&#xff0c;有很多同学在写期末Java web作业时&#xff0c;运行tomcat出现乱码问题&#xff0c;经过多次解决与研究&#xff0c;我做了如下整理&#xff1a; 原因&#xff1a; IDEA本身编码与tomcat的编码与Windows编码不同导致&#xff0c;Windows 系统控制台…...

编程新知 2026/2/10 11:13:58

【OSG学习笔记】Day 18: 碰撞检测与物理交互

物理引擎&#xff08;Physics Engine&#xff09; 物理引擎 是一种通过计算机模拟物理规律&#xff08;如力学、碰撞、重力、流体动力学等&#xff09;的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互&#xff0c;广泛应用于 游戏开发、动画制作、虚…...

编程新知 2026/2/4 2:08:30

golang循环变量捕获问题​​

在 Go 语言中&#xff0c;当在循环中启动协程&#xff08;goroutine&#xff09;时&#xff0c;如果在协程闭包中直接引用循环变量&#xff0c;可能会遇到一个常见的陷阱 - ​​循环变量捕获问题​​。让我详细解释一下&#xff1a; 问题背景 看这个代码片段&#xff1a; fo…...

编程新知 2026/1/21 14:29:57

Day131 | 灵神 | 回溯算法 | 子集型 子集

Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣&#xff08;LeetCode&#xff09; 思路&#xff1a; 笔者写过很多次这道题了&#xff0c;不想写题解了&#xff0c;大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

编程新知 2026/1/23 12:37:51

HTML 列表、表格、表单

1 列表标签 作用&#xff1a;布局内容排列整齐的区域 列表分类&#xff1a;无序列表、有序列表、定义列表。 例如&#xff1a; 1.1 无序列表 标签&#xff1a;ul 嵌套 li&#xff0c;ul是无序列表&#xff0c;li是列表条目。 注意事项&#xff1a; ul 标签里面只能包裹 li…...

编程新知 2026/1/24 22:33:33

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式

点一下关注吧&#xff01;&#xff01;&#xff01;非常感谢&#xff01;&#xff01;持续更新&#xff01;&#xff01;&#xff01; &#x1f680; AI篇持续更新中&#xff01;&#xff08;长期更新&#xff09; 目前2025年06月05日更新到&#xff1a; AI炼丹日志-28 - Aud…...

编程新知 2026/2/6 11:05:22

EtherNet/IP转DeviceNet协议网关详解

一&#xff0c;设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络&#xff0c;本网关连接到EtherNet/IP总线中做为从站使用&#xff0c;连接到DeviceNet总线中做为从站使用。 在自动…...

编程新知 2026/1/31 6:53:51

SpringCloudGateway 自定义局部过滤器

场景&#xff1a; 将所有请求转化为同一路径请求&#xff08;方便穿网配置&#xff09;在请求头内标识原来路径&#xff0c;然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

编程新知 2026/2/1 4:53:36

爬虫基础学习day2

# 爬虫设计领域 工商&#xff1a;企查查、天眼查短视频&#xff1a;抖音、快手、西瓜 ---> 飞瓜电商&#xff1a;京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空&#xff1a;抓取所有航空公司价格 ---> 去哪儿自媒体&#xff1a;采集自媒体数据进…...

编程新知 2025/12/5 3:38:11

浅谈不同二分算法的查找情况

二分算法原理比较简单&#xff0c;但是实际的算法模板却有很多&#xff0c;这一切都源于二分查找问题中的复杂情况和二分算法的边界处理&#xff0c;以下是博主对一些二分算法查找的情况分析。 需要说明的是&#xff0c;以下二分算法都是基于有序序列为升序有序的情况&#xf…...

编程新知 2025/9/14 7:37:32