基于python实现原神那维莱特开转脚本
相信不少原友都抽取了枫丹大C那维莱特,其强力的输出让不少玩家爱不释手。由于其转的越快,越不容易丢伤害的特点,很多原友在开转时容易汗流浃背,所以特意用python写了一个自动转圈脚本,当按住鼠标侧键时,即可实现高速旋转。

开转代码
首先安装pywin32库。
pip install pywin32
自动旋转代码如下:
'''
author: 巴涅波赫夫
date : 2023.12.14
ps : 请使用管理员模式打开
'''
from win32api import GetAsyncKeyState, GetCursorPos,mouse_event,Sleep
from win32con import VK_XBUTTON1, MOUSEEVENTF_MOVE # 设置鼠标侧键为目标键
target_keycode = VK_XBUTTON1def key_pressed():while True:key_state = GetAsyncKeyState(target_keycode)# 检查右方向键是否被按下if key_state < 0:print(GetCursorPos()[0], GetCursorPos()[1])# 移动鼠标到目标位置mouse_event(MOUSEEVENTF_MOVE , 5000, 0, 0, 1)Sleep(100)# 调用函数开始监听按键
key_pressed()
打包软件
使用 pyinstall 库打包成 exe 软件。
pip install pyinstaller

将软件图标与代码放在一起,并在cmd中使用如下语句打包:
pyinstall --onefile --icon=.\那维莱特.ico .\开转!.py
这时在生成的 dist 文件夹下即可找到打包后的软件。以管理员身份运行它即可快乐旋转了。
软件下载
如果不想安装python环境与打包软件,可直接前往 我的网盘 下载本软件。( 该软件为按住鼠标侧键进行转动 )
相关文章:

基于python实现原神那维莱特开转脚本
相信不少原友都抽取了枫丹大C那维莱特,其强力的输出让不少玩家爱不释手。由于其转的越快,越不容易丢伤害的特点,很多原友在开转时容易汗流浃背,所以特意用python写了一个自动转圈脚本,当按住鼠标侧键时,即可…...

C# 实现Lru缓存
C# 实现Lru缓存 LRU 算法全称是最近最少使用算法(Least Recently Use),是一种简单的缓存策略。 通常用在对象池等需要频繁获取但是又需要释放不用的地方。 代码实现的基本原理就是使用链表,当某个元素被访问时(Get或…...
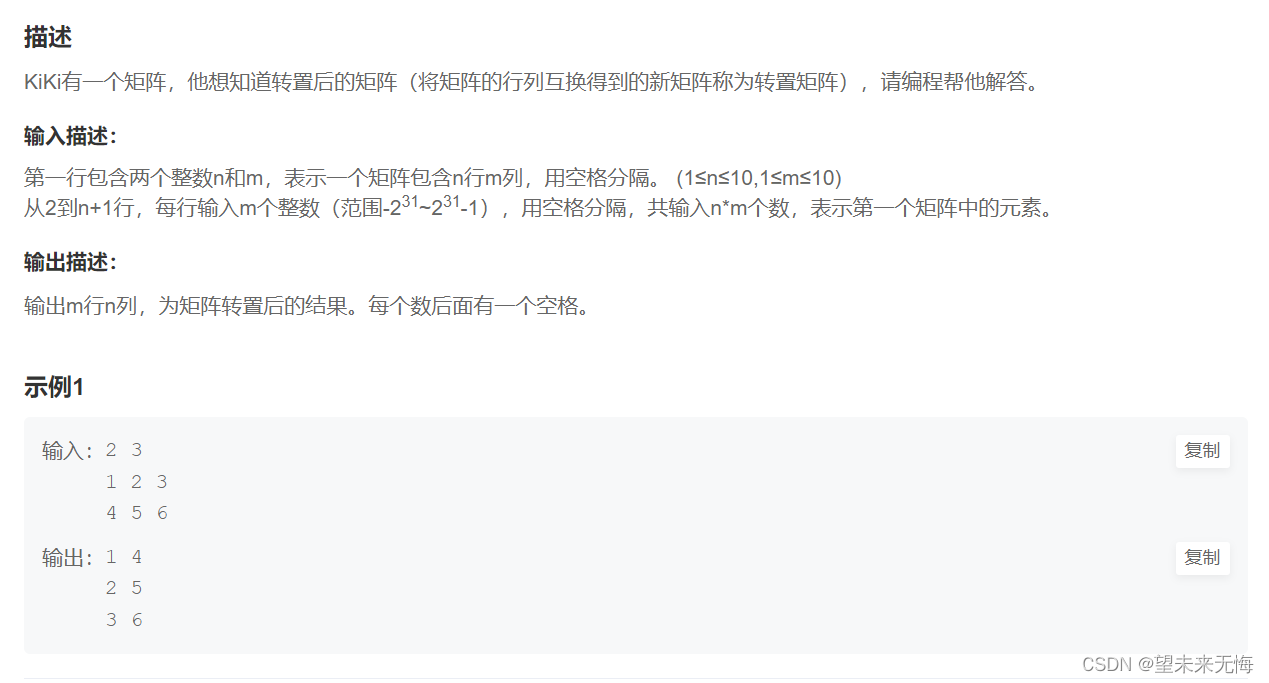
牛客网BC107矩阵转置
答案: #include <stdio.h> int main() {int n0, m0,i0,j0,a0,b0;int arr1[10][10]{0},arr2[10][10]{0}; //第一个数组用来储存原矩阵,第二个数组用来储存转置矩阵scanf("%d%d",&n,&m); if((n>1&&n<10)&&am…...

协作办公原来如此简单?详解 ONLYOFFICE 协作空间 2.0 更新
协作办公原来如此简单?详解 ONLYOFFICE 协作空间 2.0 更新 上周,ONLYOFFICE 的协作空间推出升级版 2.0 版本了: ONLYOFFICE 协作空间 2.0 现已发布:新增公共房间、插件、重新分配数据、RTL 界面等功能 ONLYOFFICE 协作空间是去…...

2023年国赛高教杯数学建模A题定日镜场的优化设计解题全过程文档及程序
2023年国赛高教杯数学建模 A题 定日镜场的优化设计 原题再现 构建以新能源为主体的新型电力系统,是我国实现“碳达峰”“碳中和”目标的一项重要措施。塔式太阳能光热发电是一种低碳环保的新型清洁能源技术[1]。 定日镜是塔式太阳能光热发电站(以下…...
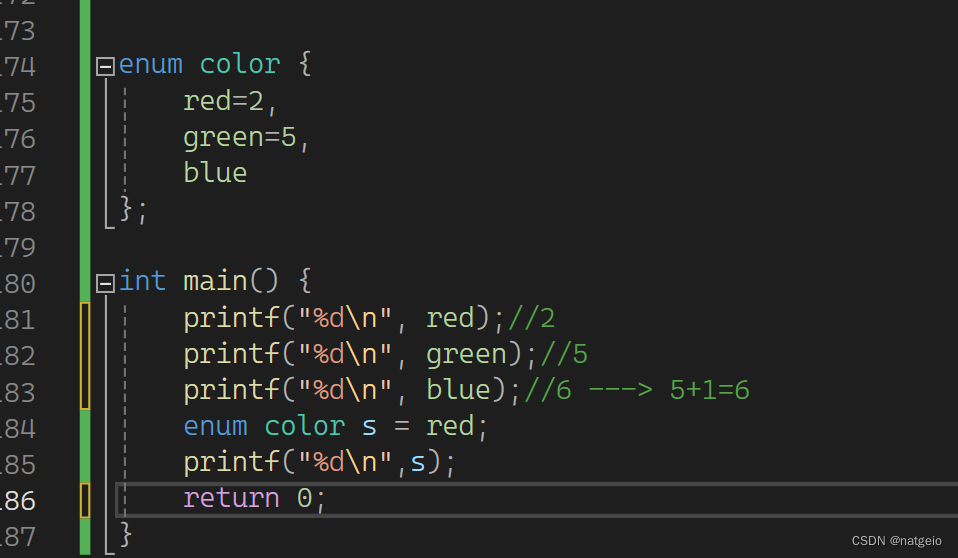
c/c++ 结构体、联合体、枚举
结构体 结构体内存对齐规则: 1、结构体的第一个成员对齐到结构体变量起始位置偏移量为0的地址处 2、其他成员变量要对齐到某个数字(对齐数)的整数倍的地址处。 对齐数:编译器默认的一个对齐数与该成员变量大小的较小值。 vs 中…...

stl模板库成员函数重载类型混肴编译不通过解决方法
stl模板库成员函数重载类型混肴编译不通过解决方法 这种方式编译不通过IsArithmetic和HasMemberList编译器存在混肴 template <typename T, typename Enable std::enable_if<IsArithmetic<T>::value>::type >static void DumpWrapper(T* filed, std::strin…...
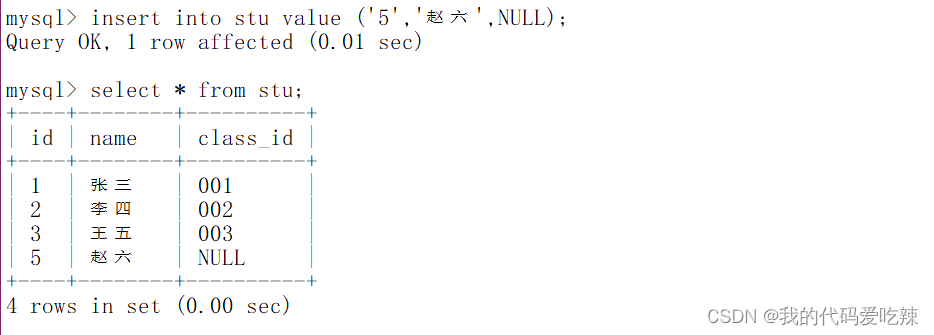
MySQL——表的约束
目录 一.表的约束 二.空属性 编辑三.默认值 四.列描述 五.主键 1.主键 2.符合主键 六.自增长 七.唯一键 八.外键 一.表的约束 真正约束字段的是数据类型,但是数据类型约束很单一,需要有一些额外的约束,更好的保证数据的合法性&…...
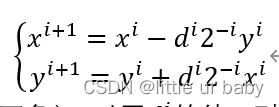
cordic 算法学习记录
参考:b站教学视频FPGA:Cordic算法介绍与实现_哔哩哔哩_bilibili FPGA硬件实现加减法、移位等操作比较简单,但是实现乘除以及函数计算复杂度高且占用资源多,常见的计算三角函数/平方根的求解方式有①查找表:先把函数对应…...

【STM32】电机驱动
一、电机分类 二、直流电机的分类 1.有刷电机 2.无刷电机 3.直流减速电机 三、H桥电路 正向旋转 驱动Q1和Q4 反向旋转 驱动Q2和Q3 四、MC3386电机驱动芯片 1.基本原理图 1)前进/后退:IN1和IN2的电平顺序决定电机的正反转 2)调节速度&#…...
)
csp 如此编码 C语言(回归唠嗑版)
熟悉的开篇废话,最近其实在研究那个web开发这一块,导致csp联系就减少了,好久没更csp的帖子了,尽管明天就要考了,但是嘞,能看一道是一道呗对吧。 等过段时间我把web开发这一块整明白了就发帖子,…...

或许是全网最全的延迟队列
什么是延迟队列 作用:用来存储延迟消息延迟消息:生产者发送一个消息给mq,然后mq会经过一段时间(延迟时间),然后在把这个消息发送给消费者 应用场景 预定会议后,需要在预定的时间点前十分钟通…...

C语言结构体小项目之通讯录代码实现+代码分析
一、思路 1.文件 这里由于通讯录实现代码较长,因此分三个文件进行,contact.c用于实现通讯录主体代码,声明各项头文件用contact.h实现,测试用test.c 二.功能 增加联系人删除联系人修改联系人查找指定联系人排序显示通讯录的信息…...
tp5 rewrite nginx重写
tp框架,默认的访问路径是 www.xxxx.com/index.php/admin/shop/index格式的,为了方便和更规范,也看起来有逼格一些,需要将index.php去掉 无index.php就会报404 我这里是宝塔 #地址重写if (!-e $request_filename) {rewrite ^(.*)$ /index.…...

.NET 反射优化的经验分享
比如针对 GetCustomAttributes 通过反射获取属性的优化,以下例子 // dotnet run -c Release -f net7.0 --filter "*" --runtimes net7.0 net8.0public class Tests{public object[] GetCustomAttributes() => typeof(C).GetCustomAttributes(typeof(MyAttribute…...

使用opencv的Sobel算子实现图像边缘检测
1 边缘检测介绍 图像边缘检测技术是图像处理和计算机视觉等领域最基本的问题,也是经典的技术难题之一。如何快速、精确地提取图像边缘信息,一直是国内外的研究热点,同时边缘的检测也是图像处理中的一个难题。早期的经典算法包括边缘算子方法…...

亿欧网首届“元创·灵镜”科技艺术节精彩纷呈,实在智能AI Agent智能体展现硬核科技图景
12月4日-10日,持续一周的首届“元创灵镜”科技艺术节在海南陵水香水湾拉开帷幕,虚实交互创造出的“海岛之镜”开幕式呈现出既真实又虚幻的未来感,融入前沿科技元素的艺术装置作品在“虚实之镜&自然生长”科技艺术展诠释着浪漫想象&#x…...
宝塔面板快速搭建本地网站结合内网穿透实现远程访问【无需公网IP】
文章目录 前言1. 环境安装2. 安装cpolar内网穿透3. 内网穿透4. 固定http地址5. 配置二级子域名6. 创建一个测试页面 前言 宝塔面板作为简单好用的服务器运维管理面板,它支持Linux/Windows系统,我们可用它来一键配置LAMP/LNMP环境、网站、数据库、FTP等&…...
css的Grid布局
1.简单布局 .grid { display: grid; grid-template-columns: 1fr 2fr 1fr; 布局样式 column-gap: 24px; 列间距 row-gap: 24px; 行间距 } 2.排列布局 center垂直方向居中对其 end靠下对齐 3.水平方向对齐 center居中 end靠右对齐 space-between两段对齐 4.对…...
Python接口测试框架选择之pytest+yaml+Allure!
一、为什么选择pytest? pytest完全兼容python自带的unittest pytest让单元测试更简单,能很好的管理测试用例。 对于实现接口测试的复杂场景,pytest的fixture、PDB等高阶用法都能实现需求。 入门简单,对于代码基础薄弱的团队人员…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...
