cordic 算法学习记录
参考:b站教学视频FPGA:Cordic算法介绍与实现_哔哩哔哩_bilibili
FPGA硬件实现加减法、移位等操作比较简单,但是实现乘除以及函数计算复杂度高且占用资源多,常见的计算三角函数/平方根的求解方式有①查找表:先把函数对应结果存在存储器中,根据输入地址确定计算结果;②泰勒展开:把三角函数等函数求解展开成乘、除、加法进行求解。这两种方法耗费ram/乘法器的资源巨大,为了仅用简单的移位/加减法运算求解出复杂三角函数,提出了cordic算法。
cordic算法:coordinate rootation digital computer 坐标旋转数字计算方法(硬件加速算法)。
类似于二分法,反复迭代,逐次逼近最终值,计算结果达到一定精度即可终止。与二分法不同的是,这里不是每次都改变二分之一的角度,而是改变二分之一的tan值,计算出对应角度,从而把复杂运算转换为简单的移位运算。
问题:已知某点坐标,①求旋转到X轴需要的角度(向量模式);②求旋转某角度后的坐标(旋转模式);

对于旋转模式:
模块输入为:坐标(x,y),要旋转的角度z。输出为:新的坐标(x1,y1)
根据新坐标的表达式,当输入x=1/k,y=0时,输出新的坐标为(cosz,sinz),即求出了cosz和sinz的值。
对于向量模式:
模块输入为:坐标(x,y),要旋转的角度z。输出为:新点的模长和角度。
根据输出的表达式,当输入为x=1,z=0时,输出为(x,y)的角度:arctan(y/x)。
除此(圆周旋转系统)之外,还有线性旋转、双曲旋转两种系统(迭代方程不同),根据需要查看文献了解。
cordic算法用途之一:求相位角!
算法原理:
已知点(x1,y1),求旋转角度z后的坐标(x2,y2);



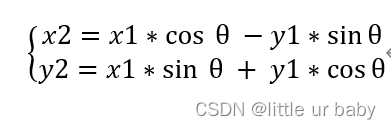

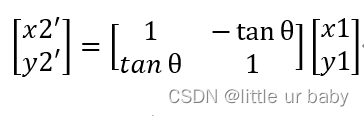

让point1以θ1、θ2...... θn逐次逼近point2(此过程需调节正负号),直到误差在可接受的范围内:

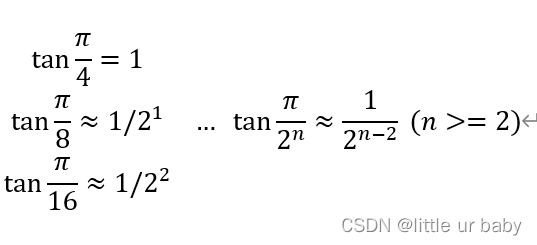
为了确保数值准确,即不取约等于,我们从函数值入手,只确保tan θn =1/2n-2 ,不去管θn的具体值,即存在

求得如下角度:

后续的旋转角度均按这个表格来旋转:
 即把求解tanx函数转化成了移位运算:
即把求解tanx函数转化成了移位运算:

求解坐标就转化成了加减运算和移位运算
对于系数cos,当角度趋近于0时,cos值趋近于1,可以知道当迭代次数足够高时,伸缩因子基本是一个常数。按照上面角度的表格,通过计算可知,当迭代次数大于16次时,伸缩因子固定为0.6073,所以我们可以设置迭代次数高于16,把伸缩因子固定为0.673,在所有运算结束后再乘上去。
相位误差取决了迭代的次数,用上述表格,当迭代次数确定为16次时,求解的相位误差小于等于18°。
假定每次坐标旋转θ,且tanθn=1/2n-2 ,则可以得出单次迭代的坐标公式(没考虑伸缩因子):
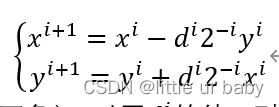
其中,di是旋转方向的判定因子(正负)。对于di的值,引入角度累加器来判定,当累加的角度大于原始角度时,di为负,小于则di为正,
cordic算法即迭代算法(如以上迭代公式),通过多次迭代降低误差,逼近目标值。
迭代有两种模式:
①串行模块:控制复杂,资源较少,速度较慢
②并行模块:资源较多,速度较快,吞吐量大
atan函数:返回(-pi/2,pi/2)范围的相位角;
atan2函数:返回(-pi,pi)范围的相位角;
项目中用的是atan2函数。
quartus cordic ip核:
包含:
①sin cos
②atan2: 返回(-pi,pi)范围的相位角;
③vector translate function:向量模式
④vector rotate function:旋转模式
quartus 的cordic IP核用modelsim-se进行仿真时需要添加altera库,暂时没有进行仿真。(貌似如果用altera-modelsim就不需要再手动添加)
cordic算法的fpga实现:
求相位角:对于串行的方法来说,只需要根据迭代的表达式通过状态机即可实现(线性序列机也可以,就是比较啰嗦,对于有相同迭代表达式的算法来说,状态机方便)。
相关文章:
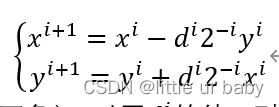
cordic 算法学习记录
参考:b站教学视频FPGA:Cordic算法介绍与实现_哔哩哔哩_bilibili FPGA硬件实现加减法、移位等操作比较简单,但是实现乘除以及函数计算复杂度高且占用资源多,常见的计算三角函数/平方根的求解方式有①查找表:先把函数对应…...

【STM32】电机驱动
一、电机分类 二、直流电机的分类 1.有刷电机 2.无刷电机 3.直流减速电机 三、H桥电路 正向旋转 驱动Q1和Q4 反向旋转 驱动Q2和Q3 四、MC3386电机驱动芯片 1.基本原理图 1)前进/后退:IN1和IN2的电平顺序决定电机的正反转 2)调节速度&#…...
)
csp 如此编码 C语言(回归唠嗑版)
熟悉的开篇废话,最近其实在研究那个web开发这一块,导致csp联系就减少了,好久没更csp的帖子了,尽管明天就要考了,但是嘞,能看一道是一道呗对吧。 等过段时间我把web开发这一块整明白了就发帖子,…...

或许是全网最全的延迟队列
什么是延迟队列 作用:用来存储延迟消息延迟消息:生产者发送一个消息给mq,然后mq会经过一段时间(延迟时间),然后在把这个消息发送给消费者 应用场景 预定会议后,需要在预定的时间点前十分钟通…...

C语言结构体小项目之通讯录代码实现+代码分析
一、思路 1.文件 这里由于通讯录实现代码较长,因此分三个文件进行,contact.c用于实现通讯录主体代码,声明各项头文件用contact.h实现,测试用test.c 二.功能 增加联系人删除联系人修改联系人查找指定联系人排序显示通讯录的信息…...
tp5 rewrite nginx重写
tp框架,默认的访问路径是 www.xxxx.com/index.php/admin/shop/index格式的,为了方便和更规范,也看起来有逼格一些,需要将index.php去掉 无index.php就会报404 我这里是宝塔 #地址重写if (!-e $request_filename) {rewrite ^(.*)$ /index.…...

.NET 反射优化的经验分享
比如针对 GetCustomAttributes 通过反射获取属性的优化,以下例子 // dotnet run -c Release -f net7.0 --filter "*" --runtimes net7.0 net8.0public class Tests{public object[] GetCustomAttributes() => typeof(C).GetCustomAttributes(typeof(MyAttribute…...

使用opencv的Sobel算子实现图像边缘检测
1 边缘检测介绍 图像边缘检测技术是图像处理和计算机视觉等领域最基本的问题,也是经典的技术难题之一。如何快速、精确地提取图像边缘信息,一直是国内外的研究热点,同时边缘的检测也是图像处理中的一个难题。早期的经典算法包括边缘算子方法…...

亿欧网首届“元创·灵镜”科技艺术节精彩纷呈,实在智能AI Agent智能体展现硬核科技图景
12月4日-10日,持续一周的首届“元创灵镜”科技艺术节在海南陵水香水湾拉开帷幕,虚实交互创造出的“海岛之镜”开幕式呈现出既真实又虚幻的未来感,融入前沿科技元素的艺术装置作品在“虚实之镜&自然生长”科技艺术展诠释着浪漫想象&#x…...
宝塔面板快速搭建本地网站结合内网穿透实现远程访问【无需公网IP】
文章目录 前言1. 环境安装2. 安装cpolar内网穿透3. 内网穿透4. 固定http地址5. 配置二级子域名6. 创建一个测试页面 前言 宝塔面板作为简单好用的服务器运维管理面板,它支持Linux/Windows系统,我们可用它来一键配置LAMP/LNMP环境、网站、数据库、FTP等&…...
css的Grid布局
1.简单布局 .grid { display: grid; grid-template-columns: 1fr 2fr 1fr; 布局样式 column-gap: 24px; 列间距 row-gap: 24px; 行间距 } 2.排列布局 center垂直方向居中对其 end靠下对齐 3.水平方向对齐 center居中 end靠右对齐 space-between两段对齐 4.对…...
Python接口测试框架选择之pytest+yaml+Allure!
一、为什么选择pytest? pytest完全兼容python自带的unittest pytest让单元测试更简单,能很好的管理测试用例。 对于实现接口测试的复杂场景,pytest的fixture、PDB等高阶用法都能实现需求。 入门简单,对于代码基础薄弱的团队人员…...

03-详解Nacos注册中心的配置步骤和功能
Nacos注册中心 服务注册到Nacos Nacos是SpringCloudAlibaba的组件也遵循SpringCloud中定义的服务注册和服务发现规范,因此使用Nacos与使用Eureka对于微服务来说并没有太大区别 主要差异就是依赖不同,服务地址不同 第一步: 在父工程cloud-demo模块的pom.xml文件中引入Spring…...

微服务学习:Nacos微服务架构中的服务注册、服务发现和动态配置Nacos下载
Nacos的主要用途包括: 服务注册与发现:Nacos提供了服务注册和发现的功能,服务提供者可以将自己的服务注册到Nacos服务器上,服务消费者则可以通过Nacos来发现可用的服务实例,从而实现服务调用。 动态配置管理ÿ…...
逆向经历回顾总结
逆向经历回顾总结 一、前言 将自己的逆向经验做个总结,希望新手对逆向大方向能快速了解。高手有啥不一样的经验也可以讨论讨论。 二、个人经历 本人入行逆向全因一部韩剧“幽灵”,里面涉及渗透、病毒分析、取证的攻防对抗,我觉得对新手来说…...

企业IT安全:内部威胁检测和缓解
什么是内部威胁 内部威胁是指由组织内部的某个人造成的威胁,他们可能会造成损害或窃取数据以谋取自己的经济利益,造成这种威胁的主要原因是心怀不满的员工。 任何内部人员,无论是员工、前雇员、承包商、第三方供应商还是业务合作伙伴&#…...
)
Linux 服务器较为强大的运维及管理脚本实现(支援:本机线上操作)
功能: Copyright (C) 2019 ~ 2023 Sichuan Jiaile Network Information Technology Co., LTD. All rights reserved. STG SCRIPT.(X) 1.0.0 VERSION Usage: ./linux.sh make 编译 ./linux.sh make ld …...
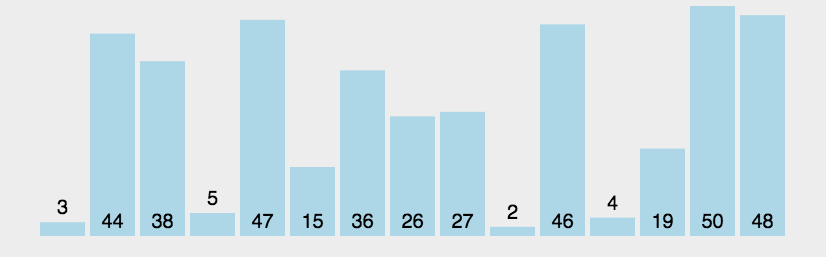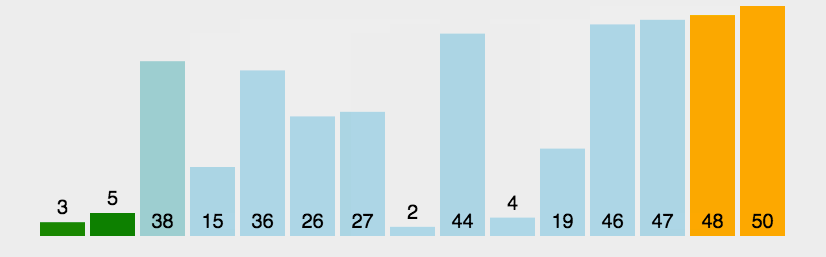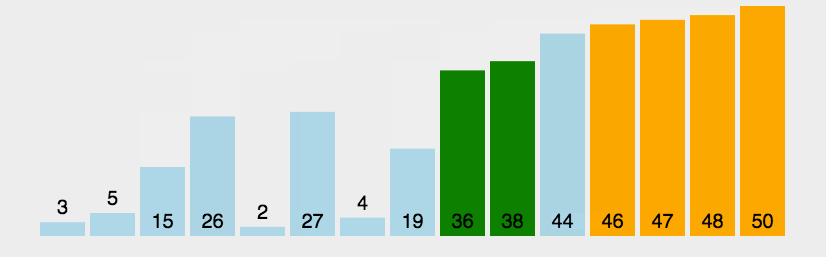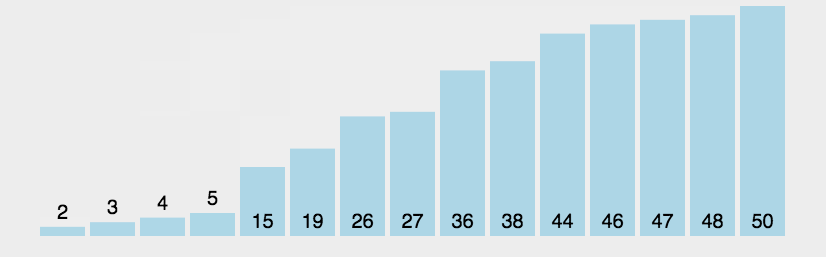
【数据结构】插入排序,希尔排序,选择排序,堆排序,冒泡排序
1.插入排序 思路:插入排序将一个数插入一个有序的数组里面,将这个数和数组元素挨着比较,直到他插入到合适的位置。 动画演示: 步骤:1.定义一个变量tmp保存要插入的数据 2.在循环中用tmp和有序数组中的元素比较&#…...
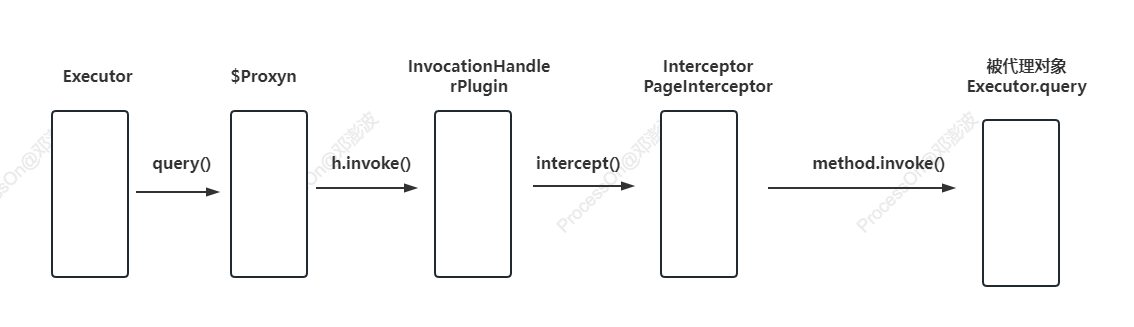
MyBatis--07--启动过程分析、SqlSession安全问题、拦截器
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 谈谈MyBatis的启动过程具体的操作过程如下:实现测试类,并测试SqlSessionFactorySqlSession SqlSession有数据安全问题?在MyBatis中,SqlSess…...
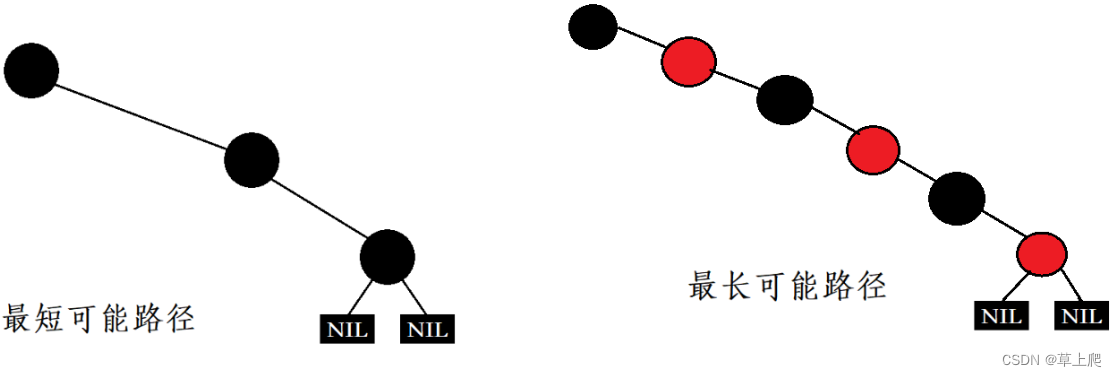
Qt基础之四十二:QMap、QHash的实现原理和性能对比
一.红黑树与哈希表 1.红黑树 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。 红黑树为了保证其最长…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

验证redis数据结构
一、功能验证 1.验证redis的数据结构(如字符串、列表、哈希、集合、有序集合等)是否按照预期工作。 2、常见的数据结构验证方法: ①字符串(string) 测试基本操作 set、get、incr、decr 验证字符串的长度和内容是否正…...

(12)-Fiddler抓包-Fiddler设置IOS手机抓包
1.简介 Fiddler不但能截获各种浏览器发出的 HTTP 请求,也可以截获各种智能手机发出的HTTP/ HTTPS 请求。 Fiddler 能捕获Android 和 Windows Phone 等设备发出的 HTTP/HTTPS 请求。同理也可以截获iOS设备发出的请求,比如 iPhone、iPad 和 MacBook 等苹…...
可视化预警系统:如何实现生产风险的实时监控?
在生产环境中,风险无处不在,而传统的监控方式往往只能事后补救,难以做到提前预警。但如今,可视化预警系统正在改变这一切!它能够实时收集和分析生产数据,通过直观的图表和警报,让管理者第一时间…...

河北对口计算机高考MySQL笔记(完结版)(2026高考)持续更新~~~~
MySQL 基础概念 数据(Data):文本,数字,图片,视频,音频等多种表现形式,能够被计算机存储和处理。 **数据库(Data Base—简称DB):**存储数据的仓库…...

分布式光纤声振传感技术原理与瑞利散射机制解析
分布式光纤传感技术(Distributed Fiber Optic Sensing,简称DFOS)作为近年来迅速发展的新型感知手段,已广泛应用于边界安防、油气管道监测、结构健康诊断、地震探测等领域。其子类技术——分布式光纤声振传感(Distribut…...
