2. 皇后的控制力
题目描述:
我们对八皇后问题进行扩展。
国际象棋中的皇后非常神勇,一个皇后可以控制横、竖、斜线等4个方向(或者说是8个方向),只要有棋子落入她的势力范围,则必死无疑,所以对方的每个棋子都要小心地躲开皇后的势力范围,选择一个合适的位置放置。如果在棋盘上有两个皇后,则新皇后控制的势力范围与第一个皇后控制的势力范围可以进行叠加,这样随着皇后数量的增加,皇后们控制的范围越来越大,直至控制了棋盘中全部的格子。
现在我们关心的是,如果在 N×N 的棋盘上放入 M 个皇后(M个皇后相互之间不能冲突)控制棋盘中的格子,则共有多少种不同的放置方法?
输入:N (N <= 10) M (M <= N)
输出:如果将 M 个皇后放入 N×N 的棋盘中可以控制全部棋盘中的格子,则不同的放置方法的数量
| 测试输入 | 期待的输出 | 时间限制 | 内存限制 | 额外进程 | |
|---|---|---|---|---|---|
| 测试用例 1 | 以文本方式显示
| 以文本方式显示
| 1秒 | 64M | 0 |
| 测试用例 2 | 以文本方式显示
| 以文本方式显示
| 1秒 | 64M | 0 |
C++代码
#include <iostream>
#include <vector>using namespace std;int totalSolutions = 0; // 用于记录不同的放置方法的数量// 检查当前位置是否安全
bool isSafe(int row, int col, const vector<string>& board, int N) {// 检查列for (int i = 0; i < row; ++i) {if (board[i][col] == 'Q') {return false;}}// 检查左上对角线for (int i = row, j = col; i >= 0 && j >= 0; --i, --j) {if (board[i][j] == 'Q') {return false;}}// 检查右上对角线for (int i = row, j = col; i >= 0 && j < N; --i, ++j) {if (board[i][j] == 'Q') {return false;}}return true;
}bool checkControl(const vector<string>& board, int N) {for (int i = 0; i < N; ++i) {for (int j = 0; j < N; ++j) {if (board[i][j] == '.') {// 检查当前空点是否被控制bool controlled = false;// 检查列for (int k = 0; k < N; ++k) {if (board[k][j] == 'Q') {controlled = true;break;}}// 检查行for (int k = 0; k < N; ++k) {if (board[i][k] == 'Q') {controlled = true;break;}}// 检查左上对角线for (int k = i, l = j; k >= 0 && l >= 0; --k, --l) {if (board[k][l] == 'Q') {controlled = true;break;}}// 检查右上对角线for (int k = i, l = j; k >= 0 && l < N; --k, ++l) {if (board[k][l] == 'Q') {controlled = true;break;}}// 检查左下对角线for (int k = i, l = j; k < N && l >= 0; ++k, --l) {if (board[k][l] == 'Q') {controlled = true;break;}}// 检查右下对角线for (int k = i, l = j; k < N && l < N; ++k, ++l) {if (board[k][l] == 'Q') {controlled = true;break;}}if (!controlled) {// 如果有任何空点没有被控制,则返回falsereturn false;}}}}// 所有空点都被控制,返回truereturn true;
}// 递归解决问题
void solveNQueensUtil(int row, int N, int M, vector<string>& board) {if (row == N) {if (M == 0 && checkControl(board, N)) {totalSolutions++; // 找到一个解决方案}return;}// 尝试在当前行的每一列放置皇后for (int i = 0; i < N; ++i) {if (isSafe(row, i, board, N)) {board[row][i] = 'Q'; // 放置皇后solveNQueensUtil(row + 1, N, M - 1, board); // 递归到下一行board[row][i] = '.'; // 回溯,移除皇后}}// 如果当前行不放置皇后,也递归到下一行solveNQueensUtil(row + 1, N, M, board);
}// 解决N皇后问题
int solveNQueens(int N, int M) {vector<string> board(N, string(N, '.'));solveNQueensUtil(0, N, M, board);return totalSolutions;
}int main() {int N, M;cin >> N >> M;cout << solveNQueens(N, M) << endl;return 0;
}相关文章:

2. 皇后的控制力
题目描述: 我们对八皇后问题进行扩展。 国际象棋中的皇后非常神勇,一个皇后可以控制横、竖、斜线等4个方向(或者说是8个方向),只要有棋子落入她的势力范围,则必死无疑,所以对方的每个棋子都要…...

南京邮电大学数据库实验二
1. 用create database命令创建电影数据库(MovieDB)。 create database MovieDB; 在创建表之前需调用一下指定的数据库: use MovieDB; 2.在电影数据库中用create table 命令创建如下5个关系模式: 创建movies表: create table Movies( ti…...

数据库 02-03 补充 SQL的子查询(where,from),子查询作为集合来比较some,exists,all(某一个,存在,所有)
子查询: where字句的子查询: 通常用in关键字: 举个例子: in关键字: not in 关键字: in 也可以用于枚举集合: where中可以用子查询来作为集合来筛选元祖。 some,all的运算符号…...
提升英语学习效率,尽在Eudic欧路词典 for Mac
Eudic欧路词典 for Mac是一款专为英语学习者打造的强大工具。无论您是初学者还是高级学习者,这款词典都能满足您的需求。 首先,Eudic欧路词典 for Mac具备丰富的词库,涵盖了各个领域的单词和释义。您可以轻松查询并学习单词的意思、用法和例…...

计算机网络英文总结
物理层 数据链路层 循环冗余校验(Cyclic Redundancy Check) 点对点协议PPP(Point-to-Point Protocol) 链路控制协议(Link Control Protocol) 网络控制协议(Network Control Protocol) 网络层(network layer) IP(Internet Protocol) 网际协议 ARP(Address…...

Spring上下文之注解模块ConfigurationMethod
博主介绍:✌全网粉丝5W+,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验✌ 博主作品:《Java项目案例》主要基于SpringBoot+MyBatis/MyBatis-plus+…...
【深度学习】强化学习(三)强化学习的目标函数
文章目录 一、强化学习问题1、交互的对象2、强化学习的基本要素3、策略(Policy)4、马尔可夫决策过程5、强化学习的目标函数1. 总回报(Return)2. 折扣回报(Discounted Return)a. 折扣率b. 折扣回报的定义 3.…...
)
Python高级算法——人工神经网络(Artificial Neural Network)
Python中的人工神经网络(Artificial Neural Network):深入学习与实践 人工神经网络是一种模拟生物神经网络结构和功能的计算模型,近年来在机器学习和深度学习领域取得了巨大成功。本文将深入讲解Python中的人工神经网络ÿ…...
深入理解JVM设计的精髓与独特之处
这是Java代码的执行过程 从软件工程的视角去深入拆解,无疑极具吸引力:首个阶段仅依赖于源高级语言的细微之处,而第二阶段则仅仅专注于目标机器语言的特质。 不可否认,在这两个编译阶段之间的衔接(具体指明中间处理步…...

fastjson序列化与反序列化的忽略
一.场景 做了一个基于springbootfastjson的小应用。A对象与B对象是OneToMany关系。A对象新增时也希望一起传递B的信息到后台进行Many端数据的新增。直接使用A对象来接收前台传递的信息,springboot会帮我们组装好对象。查询A对象时,又不希望其中的List<…...
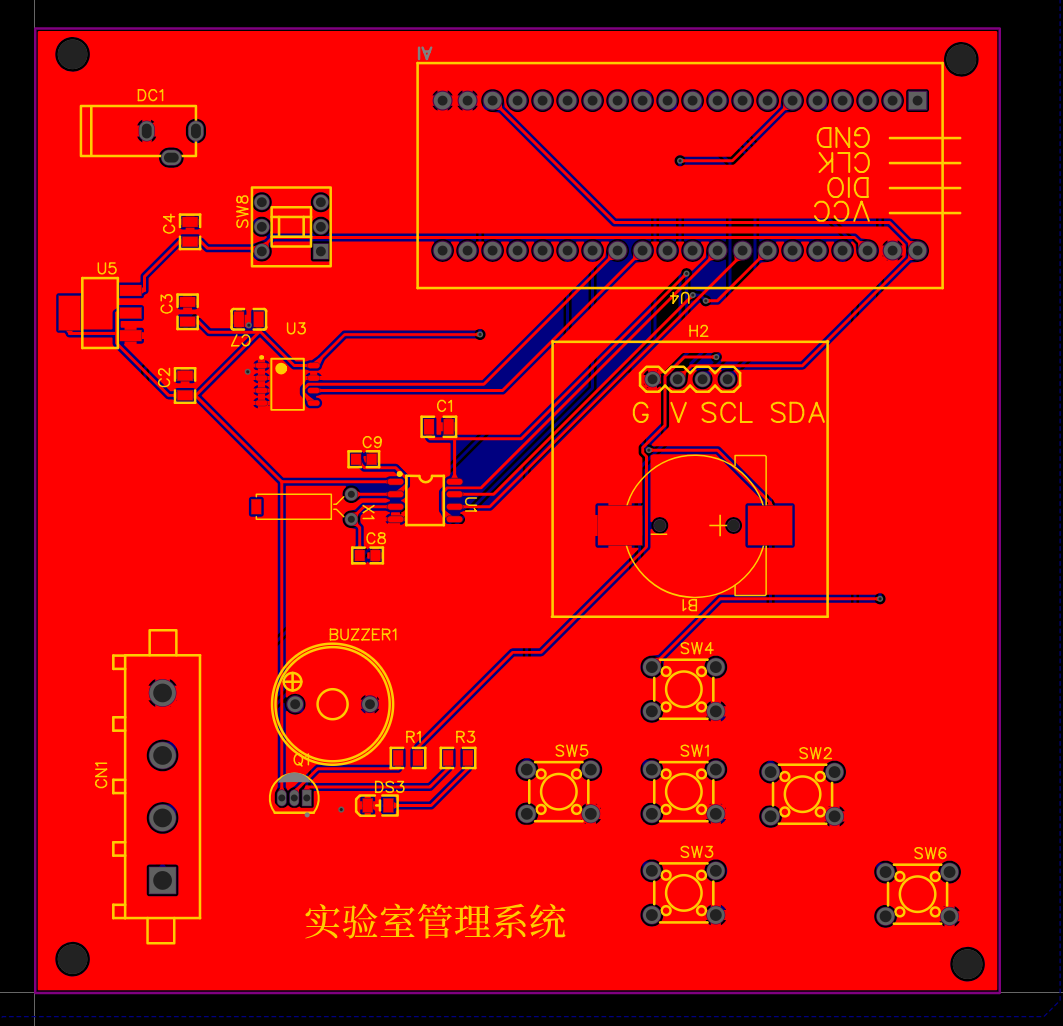
【TB作品】基于单片机的实验室管理系统,STM32,GM65二维码扫描模块
硬件: (1)STM32F103C8T6最小板() (2)GM65二维码扫描模块 (3)DS1302实时时钟模块 (4)AT24C02 存储设备 (5)蜂鸣器 …...

超过 1450 个 pfSense 服务器因错误链而遭受 RCE 攻击
在线暴露的大约 1450 个 pfSense 实例容易受到命令注入和跨站点脚本漏洞的攻击,这些漏洞如果链接起来,可能使攻击者能够在设备上执行远程代码。 pfSense 是一款流行的开源防火墙和路由器软件,允许广泛的定制和部署灵活性。 它是一种经济高效…...

react面试总结2
redux中sages和thunk中间件的区别,优缺点 Redux 中的 redux-saga 和 redux-thunk 都是中间件,用于处理异步操作,但它们有一些区别。 Redux Thunk: 简单易用:redux-thunk 是比较简单直观的中间件,它允许 …...

hive 常见存储格式和应用场景
1.存储格式 textfile、sequencefile、orc、parquet sequencefile很少使用(不介绍了),常见的主要就是orc 和 parquet 建表声明语句是:stored as textfile/orc/parquet行存储:同一条数据的不同字段都在相邻位置ÿ…...

PyPDF2库对PDF实现读取的应用
目录 一、PyPDF2 库的使用 1. 文档打开和页面读取 2. 文本提取功能 3. 示例代码...
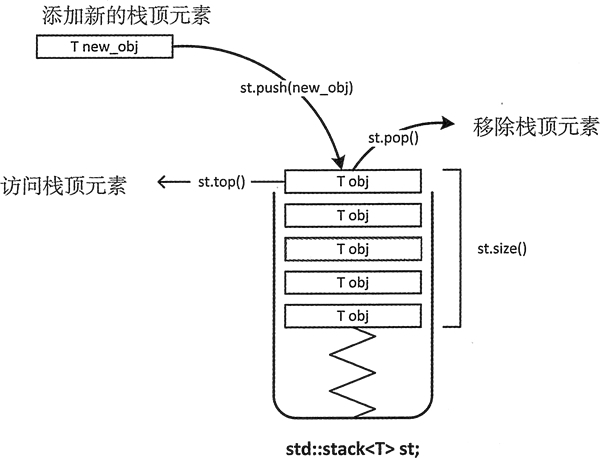
C++ stack用法详解
stack 栈适配器是一种单端开口的容器(如图 1 所示),实际上该容器模拟的就是栈存储结构,即无论是向里存数据还是从中取数据,都只能从这一个开口实现操作。 图 1 stack 适配器示意图 如图 1 所示,stack 适配器…...
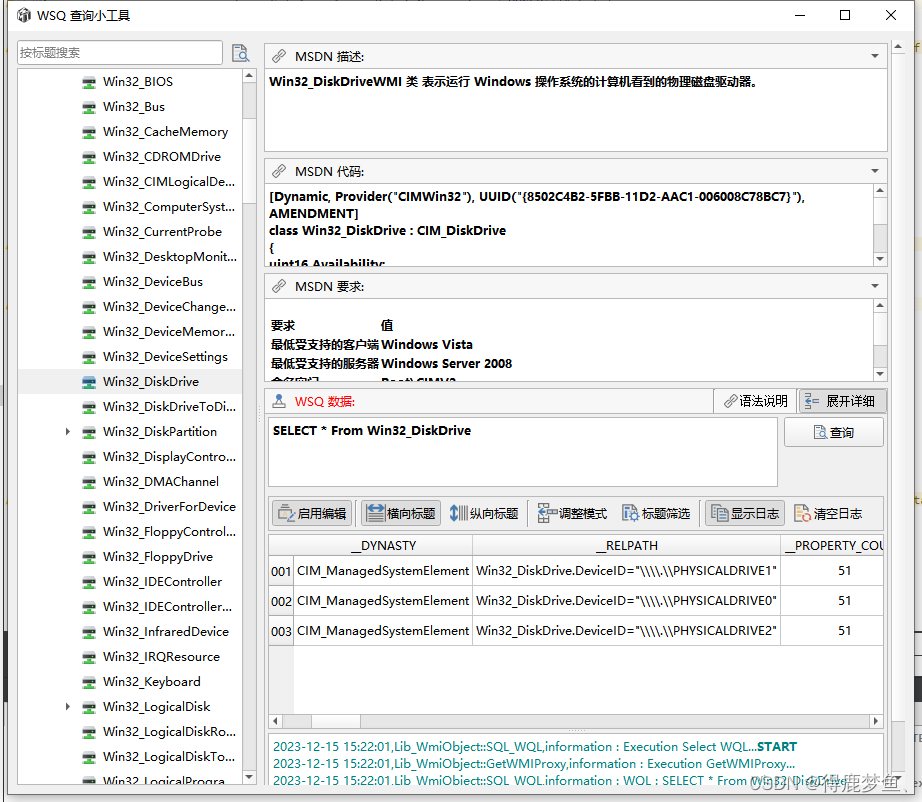
QT案例 使用WMI获取win_32类的属性值,包括Win32提供程序类中的属性
最近涉及到读取WINDOWS 系统电脑设备的各种信息,在一些特殊的PE或者简化系统中是没有WMI查询工具的,所以就自己写了个查询大部分WMI属性值的工具,免去了查网站的功夫。涉及到的方法内容就汇总做个总结。 PS:因为工作中软件基本都是我一个人开…...

TCP/UDP 的特点、区别及优缺点
1.TCP协议 传输控制协议(TCP,Transmission Control Protocol)是一种面向连接的、可靠的、基于字节流的传输层通信协议。TCP协议通过建立连接、数据确认(编段号和确认号)和数据重传等机制,保证了数据的可靠性…...
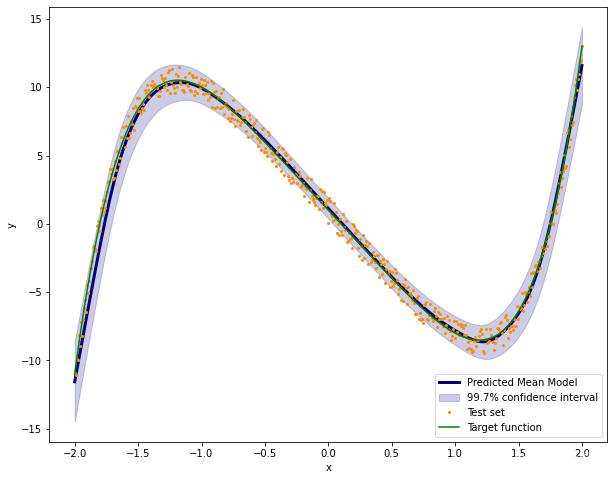
使用 Python 使用贝叶斯神经网络从理论到实践
一、说明 在本文中,我们了解了如何构建一个机器学习模型,该模型结合了神经网络的强大功能,并且仍然保持概率方法进行预测。为了做到这一点,我们可以构建所谓的贝叶斯神经网络。 这个想法不是优化神经网络的损失࿰…...
Linux 中的网站服务管理
目录 1.安装服务 2.启动服务 3.停止服务 4.重启服务 5.开机自启 6.案例 1.安装服务 网址服务程序 yum insatll httpd -y 查看所有服务 systemctl list-unit-files 2.启动服务 systemctl start httpd 查看服务进程,确认是否启动 ps -ef|grep httpd 3.停止…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
