【深度学习】强化学习(三)强化学习的目标函数
文章目录
- 一、强化学习问题
- 1、交互的对象
- 2、强化学习的基本要素
- 3、策略(Policy)
- 4、马尔可夫决策过程
- 5、强化学习的目标函数
- 1. 总回报(Return)
- 2. 折扣回报(Discounted Return)
- a. 折扣率
- b. 折扣回报的定义
- 3. 目标函数
- a. 目标函数的定义
- 2. 目标函数的解释
- 3. 优化目标
- 4、智能体走迷宫
- a. 问题
- b. 解析
一、强化学习问题
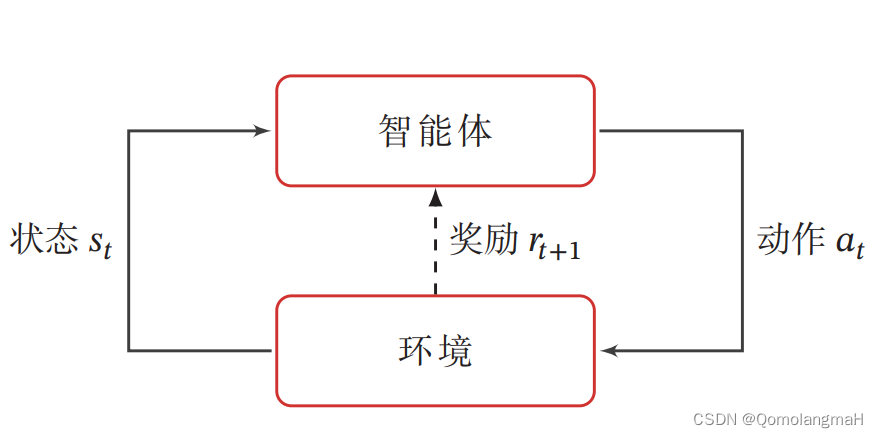
强化学习的基本任务是通过智能体与环境的交互学习一个策略,使得智能体能够在不同的状态下做出最优的动作,以最大化累积奖励。这种学习过程涉及到智能体根据当前状态选择动作,环境根据智能体的动作转移状态,并提供即时奖励的循环过程。
1、交互的对象
在强化学习中,有两个可以进行交互的对象:智能体和环境
-
智能体(Agent):能感知外部环境的状态(State)和获得的奖励(Reward),并做出决策(Action)。智能体的决策和学习功能使其能够根据状态选择不同的动作,学习通过获得的奖励来调整策略。
-
环境(Environment):是智能体外部的所有事物,对智能体的动作做出响应,改变状态,并反馈相应的奖励。
2、强化学习的基本要素
强化学习涉及到智能体与环境的交互,其基本要素包括状态、动作、策略、状态转移概率和即时奖励。
-
状态(State):对环境的描述,可能是离散或连续的。
-
动作(Action):智能体的行为,也可以是离散或连续的。
-
策略(Policy):智能体根据当前状态选择动作的概率分布。
-
状态转移概率(State Transition Probability):在给定状态和动作的情况下,环境转移到下一个状态的概率。
-
即时奖励(Immediate Reward):智能体在执行动作后,环境反馈的奖励。
3、策略(Policy)
策略(Policy)就是智能体如何根据环境状态 𝑠 来决定下一步的动作 𝑎(智能体在特定状态下选择动作的规则或分布)。
- 确定性策略(Deterministic Policy) 直接指定智能体应该采取的具体动作
- 随机性策略(Stochastic Policy) 则考虑了动作的概率分布,增加了对不同动作的探索。
上述概念可详细参照:【深度学习】强化学习(一)强化学习定义
4、马尔可夫决策过程
为了简化描述,将智能体与环境的交互看作离散的时间序列。智能体从感知到的初始环境 s 0 s_0 s0 开始,然后决定做一个相应的动作 a 0 a_0 a0,环境相应地发生改变到新的状态 s 1 s_1 s1,并反馈给智能体一个即时奖励 r 1 r_1 r1,然后智能体又根据状态 s 1 s_1 s1做一个动作 a 1 a_1 a1,环境相应改变为 s 2 s_2 s2,并反馈奖励 r 2 r_2 r2。这样的交互可以一直进行下去: s 0 , a 0 , s 1 , r 1 , a 1 , … , s t − 1 , r t − 1 , a t − 1 , s t , r t , … , s_0, a_0, s_1, r_1, a_1, \ldots, s_{t-1}, r_{t-1}, a_{t-1}, s_t, r_t, \ldots, s0,a0,s1,r1,a1,…,st−1,rt−1,at−1,st,rt,…,其中 r t = r ( s t − 1 , a t − 1 , s t ) r_t = r(s_{t-1}, a_{t-1}, s_t) rt=r(st−1,at−1,st) 是第 t t t 时刻的即时奖励。这个交互过程可以被视为一个马尔可夫决策过程(Markov Decision Process,MDP)。
关于马尔可夫决策过程可详细参照:【深度学习】强化学习(二)马尔可夫决策过程
5、强化学习的目标函数
强化学习的目标是通过学习到的策略 π θ ( a ∣ s ) \pi_{\theta}(a|s) πθ(a∣s) 来最大化期望回报(Expected Return),即希望智能体执行一系列动作以获取尽可能多的平均回报。
- 总回报:对于一次交互过程的轨迹,总回报是累积奖励的和。
- 折扣回报:引入折扣率,考虑未来奖励的权重。
1. 总回报(Return)
总回报(Total Return)指智能体与环境一次交互过程中所累积的奖励。给定一个策略 π ( a ∣ s ) \pi(a|s) π(a∣s),智能体与环境的交互过程可以通过轨迹 τ \tau τ 来表示,而这个轨迹的总回报 G ( τ ) G(\tau) G(τ) 可以通过累积奖励的方式进行计算。
-
总回报 G ( τ ) G(\tau) G(τ) 定义:
G ( τ ) = ∑ t = 0 T − 1 r t + 1 G(\tau) = \sum_{t=0}^{T-1} r_{t+1} G(τ)=t=0∑T−1rt+1其中 T T T 表示交互的总时长, r t + 1 r_{t+1} rt+1 表示在时刻 t + 1 t+1 t+1 获得的即时奖励。 -
总回报也可以通过奖励函数的形式表示:
G ( τ ) = ∑ t = 0 T − 1 r ( s t , a t , s t + 1 ) G(\tau) = \sum_{t=0}^{T-1} r(s_t, a_t, s_{t+1}) G(τ)=t=0∑T−1r(st,at,st+1)
这里, r ( s t , a t , s t + 1 ) r(s_t, a_t, s_{t+1}) r(st,at,st+1) 表示在状态 s t s_t st 下执行动作 a t a_t at 后转移到状态 s t + 1 s_{t+1} st+1 所获得的奖励。
2. 折扣回报(Discounted Return)
a. 折扣率
对于存在终止状态(Terminal State)的任务,当智能体到达终止状态时,交互过程结束,这一轮的交互称为一个回合(Episode)或试验(Trial)。一般强化学习任务都是回合式任务(Episodic Task),如下棋、玩游戏等。
然而,对于一些持续式任务(Continuing Task),其中不存在终止状态,智能体的交互可以无限进行下去,即 T = ∞ T = \infty T=∞。在这种情况下,总回报可能会无穷大。为了解决这个问题,引入了折扣率 γ \gamma γ。
b. 折扣回报的定义
-
折扣回报(Discounted Return)定义:
G ( τ ) = ∑ t = 0 T − 1 γ t r t + 1 G(\tau) = \sum_{t=0}^{T-1} \gamma^t r_{t+1} G(τ)=t=0∑T−1γtrt+1
其中 γ \gamma γ 是折扣率, γ ∈ [ 0 , 1 ] \gamma \in [0, 1] γ∈[0,1]。折扣率的引入可以看作是对未来奖励的一种降权,即智能体更加关注即时奖励和近期奖励,而对于远期奖励的关注逐渐减弱。- 当 γ \gamma γ 接近于 1 时,更加关注长期回报;
- 当 γ \gamma γ 接近于 0 时,更加关注短期回报。
-
折扣回报的定义在数学上确保了总回报的有限性,同时在实际应用中使得智能体更好地平衡长期和短期回报。
3. 目标函数
强化学习的目标是通过学习一个良好的策略来使智能体在与环境的交互中获得尽可能多的平均回报。
a. 目标函数的定义
强化学习的目标函数 J ( θ ) J(\theta) J(θ) 定义如下:
J ( θ ) = E τ ∼ p θ ( τ ) [ G ( τ ) ] = E τ ∼ p θ ( τ ) [ ∑ t = 0 T − 1 γ t r t + 1 ] J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[G(\tau)] = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t=0}^{T-1} \gamma^t r_{t+1}\right] J(θ)=Eτ∼pθ(τ)[G(τ)]=Eτ∼pθ(τ)[t=0∑T−1γtrt+1]其中, θ \theta θ 表示策略函数的参数, τ \tau τ 表示强化学习的轨迹。
- 这个目标函数表达的是在策略 π θ \pi_{\theta} πθ 下,智能体与环境交互得到的总回报的期望。(这个期望是对所有可能的轨迹进行的)
2. 目标函数的解释
- J ( θ ) J(\theta) J(θ) 可以看作是在策略 π θ \pi_{\theta} πθ 下执行动作序列的期望回报。
- 引入折扣率 γ \gamma γ 是为了在计算期望回报时对未来奖励进行折扣,使得智能体更加关注即时奖励和近期奖励。
- 目标函数 J ( θ ) J(\theta) J(θ) 的最大化等价于寻找最优的策略参数 θ \theta θ,使得智能体在与环境的交互中获得最大的长期回报。
3. 优化目标
强化学习的优化目标就是通过调整策略函数的参数 θ \theta θ,使得目标函数 J ( θ ) J(\theta) J(θ) 达到最大值。这个优化问题通常通过梯度上升等优化方法来解决,其中梯度由策略梯度定理给出。
4、智能体走迷宫
a. 问题
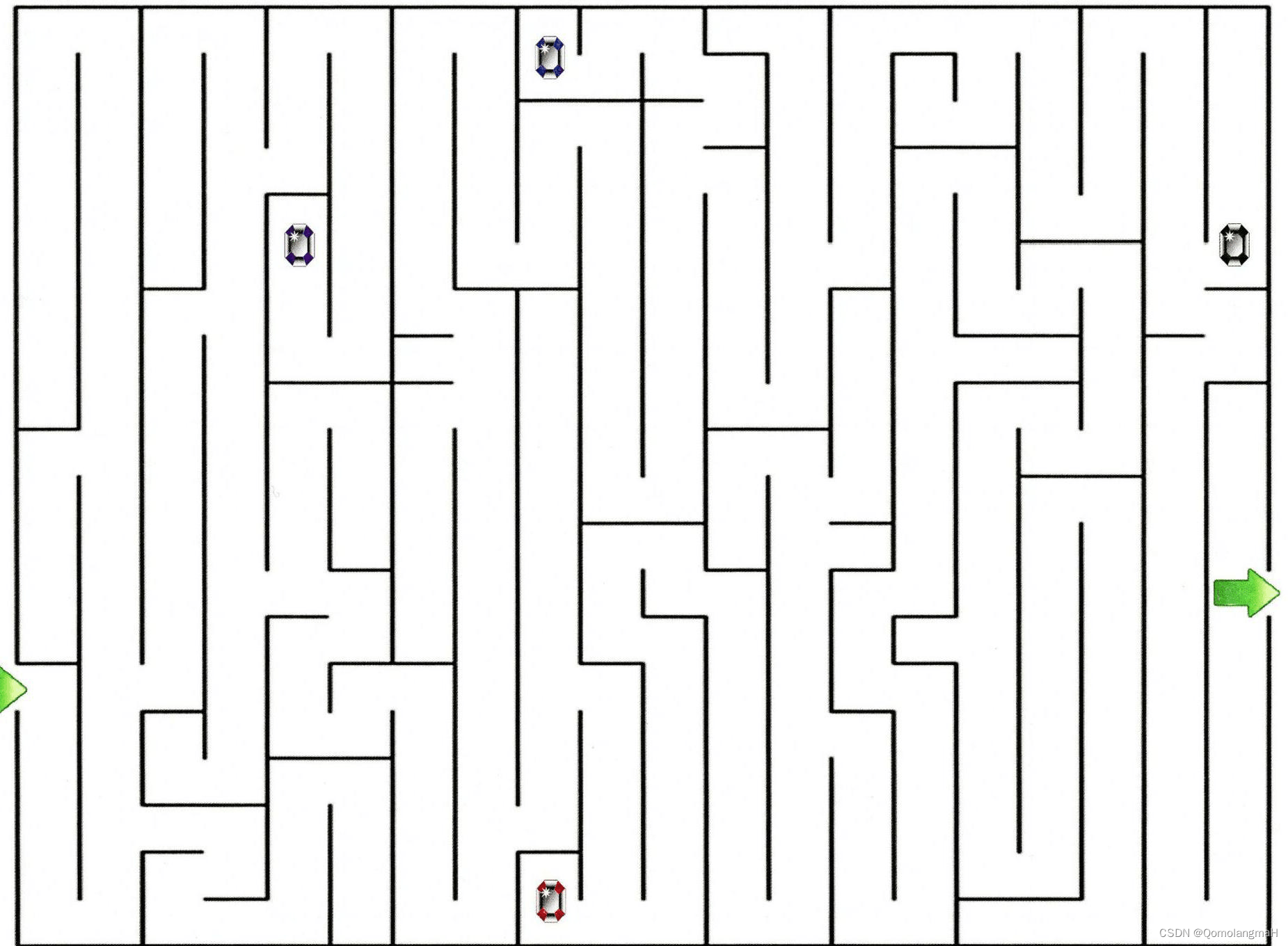
让一个智能体通过强化学习来学习走迷宫,如果智能体走出迷宫,奖励为 +1,其他状态奖励为 0.智能体的目标是最大化期望回报.当折扣率 𝛾 = 1 时,智能体是否能学会走迷宫的技巧?如何改进?
b. 解析
走迷宫任务存在终止状态(即走出迷宫),为回合式任务,智能体的交互不会无限地进行下去。由题意,当智能体出迷宫时有奖励+1,其他时刻奖励均为0。若折扣率为1,当该策略无法走出迷宫时,不会取得回报;当该策略可以走出迷宫,虽然达到了目标,但或许存在“绕远”的情况,即此时不一定为最优策略。
- 改进
- 尝试不同的折扣率:尝试使用较小的折扣率(0~1之间),以降低远期回报的权重,更强调即时奖励,加速学习过程。由目标函数可知,折扣率在0-1之间时,T越小则J越优,即智能体会学习到一个尽量快地走到终点的策略。
- 限制轨迹长度: 智能体会存在n个能够走出迷宫的轨迹(原地徘徊、来回绕路……),若考虑限制每个轨迹的长度,则可防止智能体无限地试验,更有可能学到直接走出迷宫的策略。
- 设置更复杂的奖励结构:尝试在迷宫中的每走一步都给予负奖励-1,在成功走出迷宫时给予大的正奖励100,以鼓励智能体更快地找到走出迷宫的策略。
- 使用深度强化学习:例如深度 Q 网络(DQN)或者深度确定性策略梯度(DDPG),这些方法通常可以更好地处理复杂的状态空间和动作空间,提高学习的效率。
相关文章:

【深度学习】强化学习(三)强化学习的目标函数
文章目录 一、强化学习问题1、交互的对象2、强化学习的基本要素3、策略(Policy)4、马尔可夫决策过程5、强化学习的目标函数1. 总回报(Return)2. 折扣回报(Discounted Return)a. 折扣率b. 折扣回报的定义 3.…...
)
Python高级算法——人工神经网络(Artificial Neural Network)
Python中的人工神经网络(Artificial Neural Network):深入学习与实践 人工神经网络是一种模拟生物神经网络结构和功能的计算模型,近年来在机器学习和深度学习领域取得了巨大成功。本文将深入讲解Python中的人工神经网络ÿ…...
深入理解JVM设计的精髓与独特之处
这是Java代码的执行过程 从软件工程的视角去深入拆解,无疑极具吸引力:首个阶段仅依赖于源高级语言的细微之处,而第二阶段则仅仅专注于目标机器语言的特质。 不可否认,在这两个编译阶段之间的衔接(具体指明中间处理步…...

fastjson序列化与反序列化的忽略
一.场景 做了一个基于springbootfastjson的小应用。A对象与B对象是OneToMany关系。A对象新增时也希望一起传递B的信息到后台进行Many端数据的新增。直接使用A对象来接收前台传递的信息,springboot会帮我们组装好对象。查询A对象时,又不希望其中的List<…...
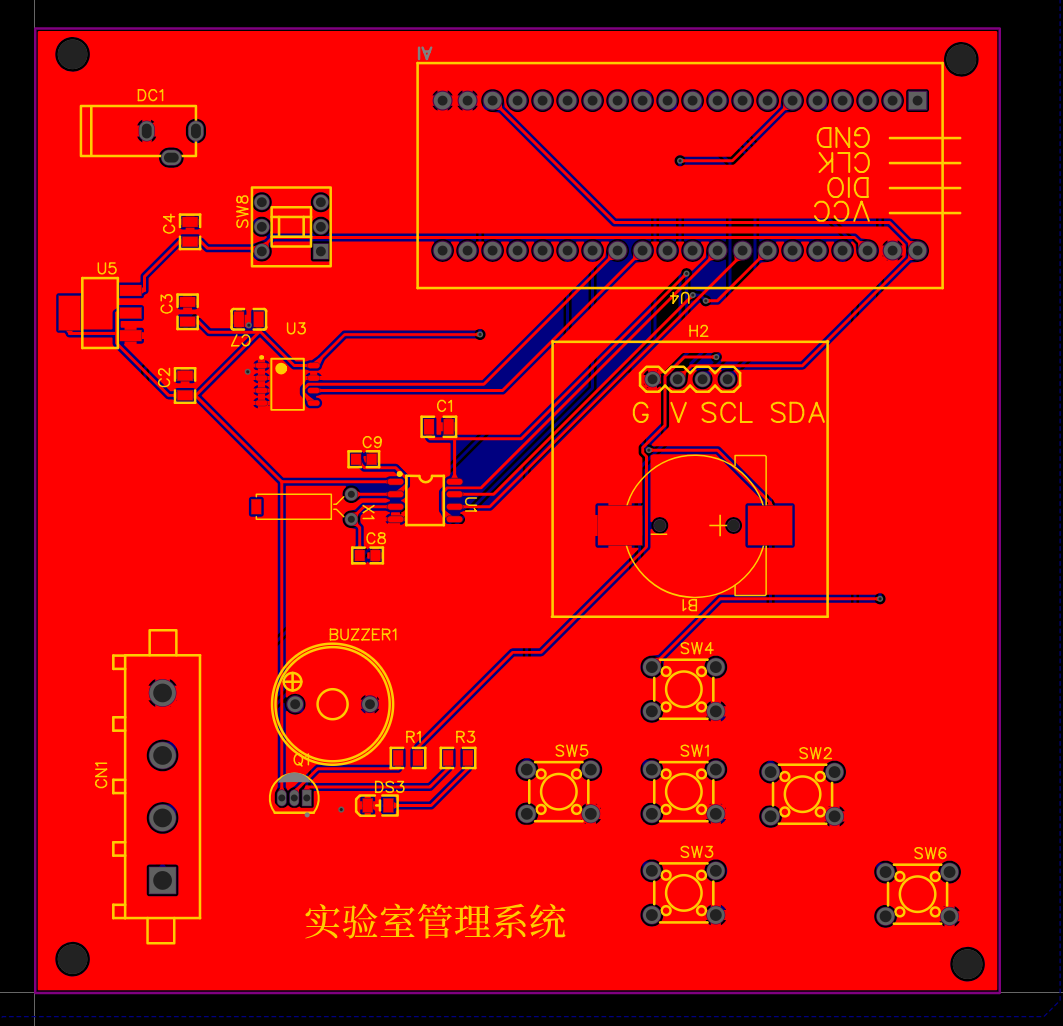
【TB作品】基于单片机的实验室管理系统,STM32,GM65二维码扫描模块
硬件: (1)STM32F103C8T6最小板() (2)GM65二维码扫描模块 (3)DS1302实时时钟模块 (4)AT24C02 存储设备 (5)蜂鸣器 …...

超过 1450 个 pfSense 服务器因错误链而遭受 RCE 攻击
在线暴露的大约 1450 个 pfSense 实例容易受到命令注入和跨站点脚本漏洞的攻击,这些漏洞如果链接起来,可能使攻击者能够在设备上执行远程代码。 pfSense 是一款流行的开源防火墙和路由器软件,允许广泛的定制和部署灵活性。 它是一种经济高效…...

react面试总结2
redux中sages和thunk中间件的区别,优缺点 Redux 中的 redux-saga 和 redux-thunk 都是中间件,用于处理异步操作,但它们有一些区别。 Redux Thunk: 简单易用:redux-thunk 是比较简单直观的中间件,它允许 …...

hive 常见存储格式和应用场景
1.存储格式 textfile、sequencefile、orc、parquet sequencefile很少使用(不介绍了),常见的主要就是orc 和 parquet 建表声明语句是:stored as textfile/orc/parquet行存储:同一条数据的不同字段都在相邻位置ÿ…...

PyPDF2库对PDF实现读取的应用
目录 一、PyPDF2 库的使用 1. 文档打开和页面读取 2. 文本提取功能 3. 示例代码...
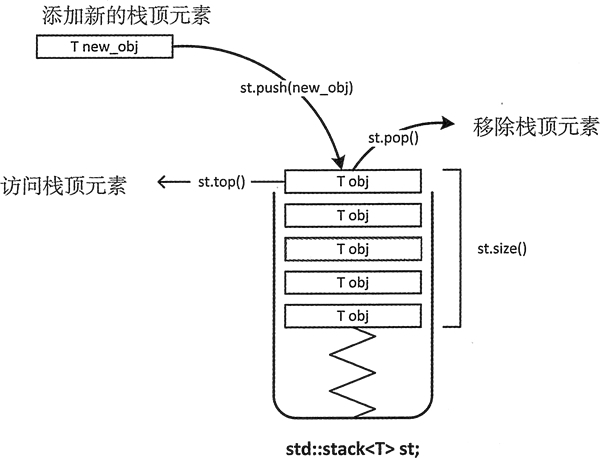
C++ stack用法详解
stack 栈适配器是一种单端开口的容器(如图 1 所示),实际上该容器模拟的就是栈存储结构,即无论是向里存数据还是从中取数据,都只能从这一个开口实现操作。 图 1 stack 适配器示意图 如图 1 所示,stack 适配器…...
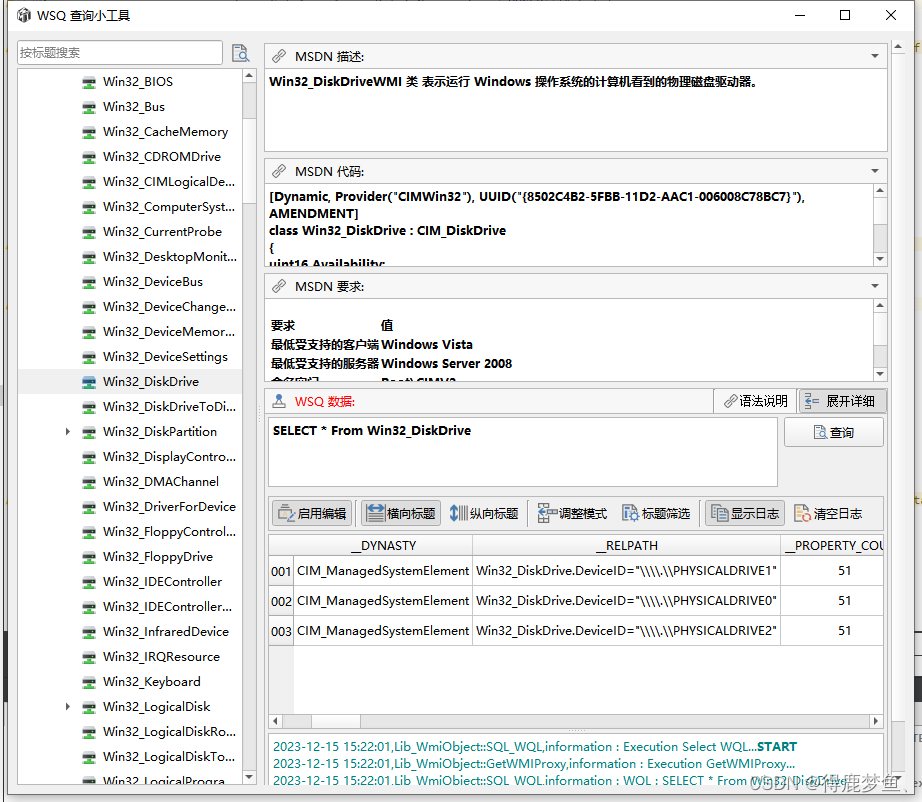
QT案例 使用WMI获取win_32类的属性值,包括Win32提供程序类中的属性
最近涉及到读取WINDOWS 系统电脑设备的各种信息,在一些特殊的PE或者简化系统中是没有WMI查询工具的,所以就自己写了个查询大部分WMI属性值的工具,免去了查网站的功夫。涉及到的方法内容就汇总做个总结。 PS:因为工作中软件基本都是我一个人开…...

TCP/UDP 的特点、区别及优缺点
1.TCP协议 传输控制协议(TCP,Transmission Control Protocol)是一种面向连接的、可靠的、基于字节流的传输层通信协议。TCP协议通过建立连接、数据确认(编段号和确认号)和数据重传等机制,保证了数据的可靠性…...
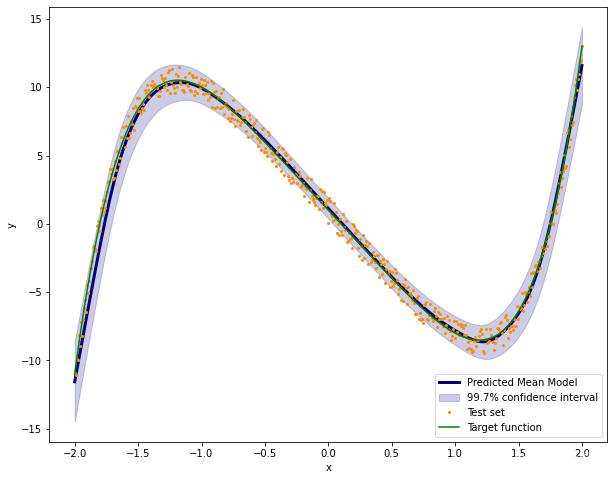
使用 Python 使用贝叶斯神经网络从理论到实践
一、说明 在本文中,我们了解了如何构建一个机器学习模型,该模型结合了神经网络的强大功能,并且仍然保持概率方法进行预测。为了做到这一点,我们可以构建所谓的贝叶斯神经网络。 这个想法不是优化神经网络的损失࿰…...
Linux 中的网站服务管理
目录 1.安装服务 2.启动服务 3.停止服务 4.重启服务 5.开机自启 6.案例 1.安装服务 网址服务程序 yum insatll httpd -y 查看所有服务 systemctl list-unit-files 2.启动服务 systemctl start httpd 查看服务进程,确认是否启动 ps -ef|grep httpd 3.停止…...
阿里云cdn设置相同的域名路径访问不同的oss目录
1.设置回源配置,添加回源URL改写 2.设置跨域,cdn的跨域优先oss 3.回源设置...
工程中提示词的开发优化基础概念学习总结)
提示(Prompt)工程中提示词的开发优化基础概念学习总结
本文对学习过程进行总结,仅对基本思路进行说明,结果在不同的模型上会有差异。 提示与提示工程 提示:指的是向大语言模型输入的特定短语或文本,用于引导模型产生特定的输出,以便模型能够生成符合用户需求的回应。 提示…...

C#基础——语法学习
C#的基本语法 在介绍基本语法之前我们先来大概讲一下创建好的这些文件都是做什么的 .sln文件:将项目和解决方案项结合到一起 .vs文件夹:用来存储当前解决方案中关于用户的设置和自定义项,比如断点,主题等。(一般都将其…...
vue-实现高德地图-省级行政区地块显示+悬浮显示+标签显示
<template><div><div id"container" /><div click"showFn">显示</div><div click"removeFn">移除</div></div> </template><script> import AMapLoader from amap/amap-jsapi-load…...

flutter ‘Gradle Libs‘ was added by build file ‘app/build.gradle‘
相关问题解释文章 How to prefer settings.gradle repositories over build.gradle repositoriesMode 解释 问题描述 此问题是,直接创建的flutter项目,需要配置其他的maven仓库地址,和第三方module,结果始终都是无法成功 错误…...

Java中的链式编程风格与应用案例
引言 链式编程是一种在编程中经常使用的风格,它可以使代码更加简洁、易读和易于维护。在Java中,链式编程可以通过方法链的方式来实现。本文将介绍Java中的链式编程风格,并通过几个应用案例来说明其实际应用。 一、链式编程的概念与特点 链式…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...