Java中的链式编程风格与应用案例
引言
链式编程是一种在编程中经常使用的风格,它可以使代码更加简洁、易读和易于维护。在Java中,链式编程可以通过方法链的方式来实现。本文将介绍Java中的链式编程风格,并通过几个应用案例来说明其实际应用。
一、链式编程的概念与特点
链式编程是一种将多个方法调用连在一起的编程风格。在链式编程中,每个方法的返回值都是一个对象,可以继续调用该对象的其他方法。这种方式使得代码看起来更加流畅,减少了临时变量的使用,提高了代码的可读性和可维护性。
链式编程的特点有以下几点:
1. 每个方法的返回值都是一个对象,可以继续调用该对象的其他方法。
2. 方法的调用顺序可以任意调整,只要保证方法之间的依赖关系正确即可。
3. 链式编程可以嵌套使用,即在一个方法中调用另一个方法,形成多层的链式调用。
二、链式编程的应用案例
1. 字符串操作
在Java中,字符串是一个常用的数据类型。使用链式编程可以方便地进行字符串的各种操作。
例如,我们需要对一个字符串进行去除空格、转换为大写、截取前5个字符的操作。使用链式编程可以写成如下形式:
String result = " hello world "
.trim()
.toUpperCase()
.substring(0, 5);
在上述代码中,首先调用了trim()方法去除字符串两端的空格,然后调用了toUpperCase()方法将字符串转换为大写,最后调用了substring()方法截取前5个字符。通过链式编程,我们可以一目了然地看出代码的执行顺序,而不需要使用临时变量来保存中间结果。
2. 集合操作
链式编程也可以用于集合的操作。例如,我们需要对一个整型列表进行筛选、排序和求和的操作。
List<Integer> numbers = Arrays.asList(1, 2, 3, 4, 5);
int sum = numbers.stream()
.filter(n -> n % 2 == 0)
.sorted()
.mapToInt(Integer::intValue)
.sum();
在上述代码中,首先使用stream()方法将列表转换为流,然后使用filter()方法筛选出偶数,接着使用sorted()方法对偶数进行排序,再使用mapToInt()方法将偶数转换为整型,最后使用sum()方法求和。通过链式编程,我们可以一步一步地对集合进行操作,使得代码更加简洁和易读。
3. 构建对象
链式编程也可以用于构建对象。例如,我们需要构建一个学生对象,包含姓名、年龄和性别等属性。
Student student = new Student()
.setName("张三")
.setAge(18)
.setGender("男");
在上述代码中,首先创建了一个学生对象,然后使用setName()、setAge()和setGender()方法分别设置学生的姓名、年龄和性别。通过链式编程,我们可以一行代码完成学生对象的构建,使得代码更加简洁和易于扩展。
结论
链式编程是一种简洁、易读和易于维护的编程风格。在Java中,链式编程可以通过方法链的方式来实现。本文介绍了链式编程的概念与特点,并通过几个应用案例来说明其实际应用。通过链式编程,我们可以使代码更加流畅,减少临时变量的使用,提高代码的可读性和可维护性。在实际开发中,我们可以根据需求选择是否使用链式编程,以提高代码的效率和质量。
相关文章:

Java中的链式编程风格与应用案例
引言 链式编程是一种在编程中经常使用的风格,它可以使代码更加简洁、易读和易于维护。在Java中,链式编程可以通过方法链的方式来实现。本文将介绍Java中的链式编程风格,并通过几个应用案例来说明其实际应用。 一、链式编程的概念与特点 链式…...
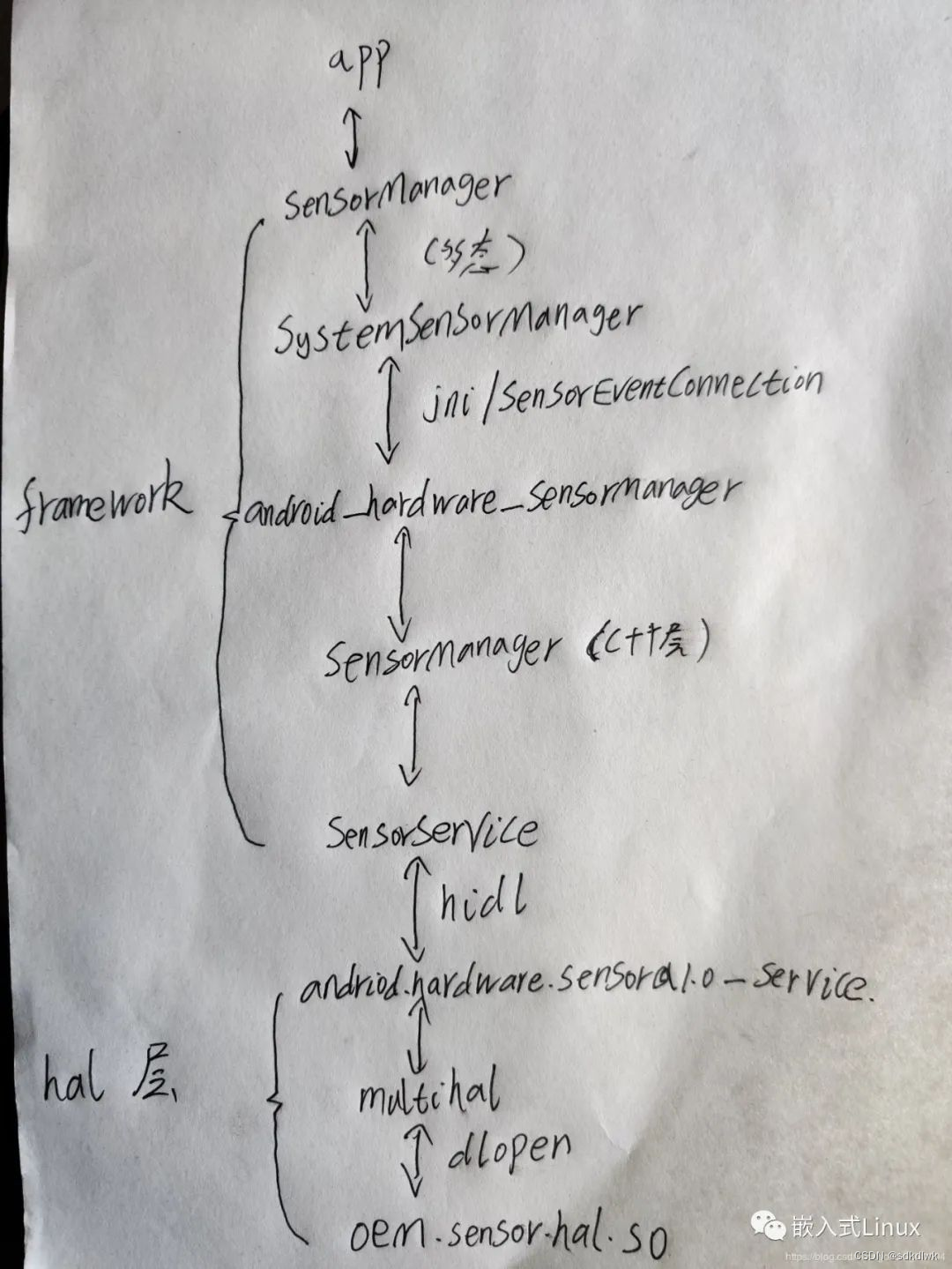
MTK Android P Sensor架构(一)
需求场景: 本来如果只是给传感器写个驱动并提供能读取温湿度数据的节点,是一件比较轻松的事情,但是最近上层应用的同事要求我们按照安卓标准的流程来,这样他们就能通过注册一个服务直接读取传感器事件数据了。这样做的好处就是第…...

低代码开发与传统软件开发:未来趋势与竞争格局
近年来,低代码开发平台的快速发展引起了各行各业的广泛关注。低代码开发平台简化了软件开发的复杂性,提供了更快速、更灵活的开发方式。于是,许多人开始产生一个疑问:未来低代码开发是否会取代传统软件开发?今天这篇文…...

leetcode 股票问题全序列
1 只允许一次交易,121题,买卖股票的最佳时机 class Solution {/*给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票…...

SpringBoot中日志的使用log4j2
SpringBoot中日志的使用log4j2 1、log4j2介绍 Apache Log4j2 是对 Log4j 的升级,它比其前身 Log4j 1.x 提供了重大改进,并提供了 Logback 中可用的许多改 进,同时修复了 Logback 架构中的一些问题,主要有: 异常处理…...
机械设备企业网站建设的效果如何
机械设备涵盖的类目比较广,其市场需求也是稳增不减,也因此无论大小企业都有增长的机会,当然这也需要靠谱的工具及正确的决策。 对机械设备企业来说,产品品质自然是首位,而向外打造品牌、扩展信息及拓客转化自然也是非…...

设计模式之结构型设计模式(二):工厂模式 抽象工厂模式 建造者模式
工厂模式 Factory 1、什么是工厂模式 工厂模式旨在提供一种统一的接口来创建对象,而将具体的对象实例化的过程延迟到子类或者具体实现中。有助于降低客户端代码与被创建对象之间的耦合度,提高代码的灵活性和可维护性。 定义了一个创建对象的接口&…...

算法模板之单链表图文讲解
🌈个人主页:聆风吟 🔥系列专栏:算法模板、数据结构 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️使用数组模拟单链表讲解1.1 🔔为什么我们要使用数组去模拟单链表…...

【强化学习-读书笔记】表格型问题的 Model-Free 方法
参考 Reinforcement Learning, Second Edition An Introduction By Richard S. Sutton and Andrew G. Barto无模型方法 在前面的文章中,我们介绍的是有模型方法(Model-Based)。在强化学习中,"Model"可以理解为算法…...

【手撕算法系列】k-means
k-means k-means算法介绍 k-means算法介绍 K-means算法是一种用于聚类的迭代算法,它将数据集划分为K个簇,其中每个数据点属于与其最近的簇的中心。这个算法的目标是最小化簇内的平方和误差(簇内数据点与簇中心的距离的平方和)。 …...

D33|动态规划!启程!
1.动态规划五部曲: 1)确定dp数组(dp table)以及下标的含义 2)确定递推公式 3)dp数组如何初始化 4)确定遍历顺序 5)举例推导dp数组 2.动态规划应该如何debug 找问题的最好方式就是把…...
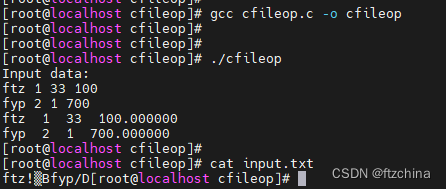
C语言----文件操作(二)
在上一篇文章中我们简单介绍了在C语言中文件是什么以及文件的打开和关闭操作,在实际工作中,我们不仅仅是要打开和关闭文件,二是需要对文件进行增删改写。本文将详细介绍如果对文件进行安全读写。 一,以字符形式读写文件ÿ…...

oracle 10046事件跟踪
10046事件是一个很好的排查sql语句执行缓慢的内部事件,具体设置方式如下: 根据10046事件跟踪SQL语句 1、 alter session set events 10046 trace name context forever,level 12; 2、执行SQL语句 3、关闭10046事件 alter session set events 10046 trace…...
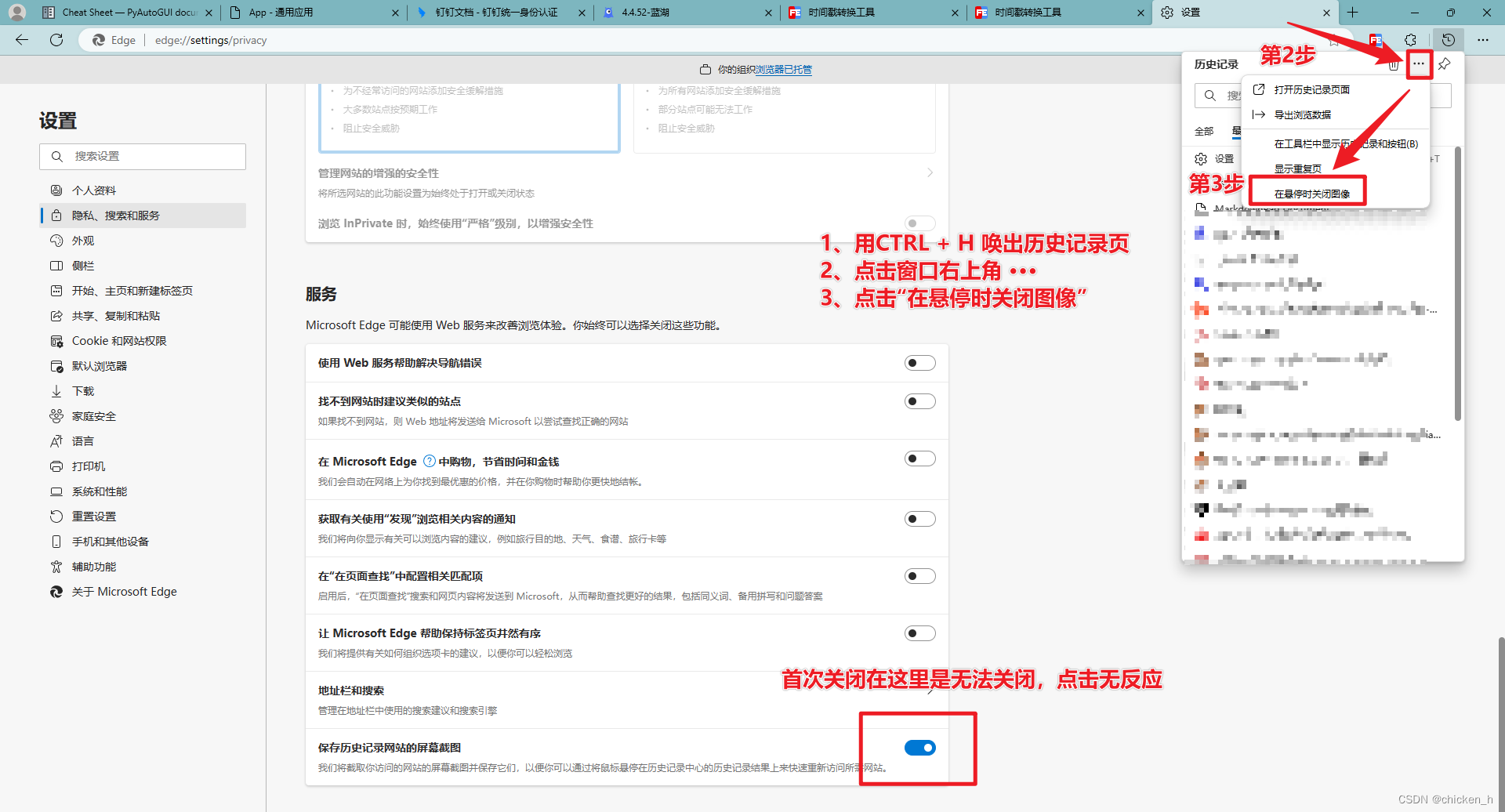
微软自带浏览器Edge,无法关闭“保存历史记录网站的屏幕截图”解决方案
微软自带浏览器Edge,无法关闭“保存历史记录网站的屏幕截图”解决方案 吐槽1:Windows自带的Chrome内核版本的浏览器Microsofg Edge刚发布时可谓一股清流,启动速度快,占用内存较小,相信很多人也开始抛弃正代Chrome&…...

讲座 | 颠覆传统摄像方式乃至计算机视觉的“脉冲视觉”
传统相机拍摄视频时其实是以一定帧率进行采样,视频其实还是一串图片的集合,因此低帧率时会觉得视频卡,拍摄高速运动物体时会有运动模糊等等问题。然而你能想象这一切都可以被“脉冲视觉”这一前沿技术改变吗? 今天下午听了北京大学…...
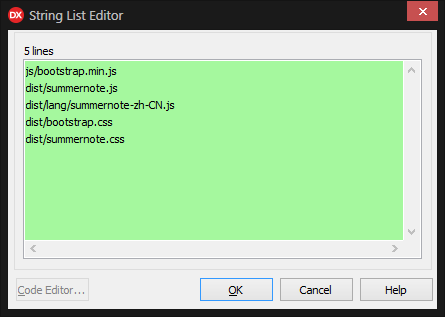
uniGUI学习之UniHTMLMemo1富文本编辑器
1]系统自带的富文本编辑器 2]jQueryBootstarp富文本编辑器插件summernote.js 1]系统自带的富文本编辑器 1、末尾增加<p> 2、增加字体 3、解决滚屏问题 4、输入长度限制问题 5、显示 并 编辑 HTML源代码(主要是图片处理) 1、末尾增加<p> UniHTMLMemo1.Lines…...
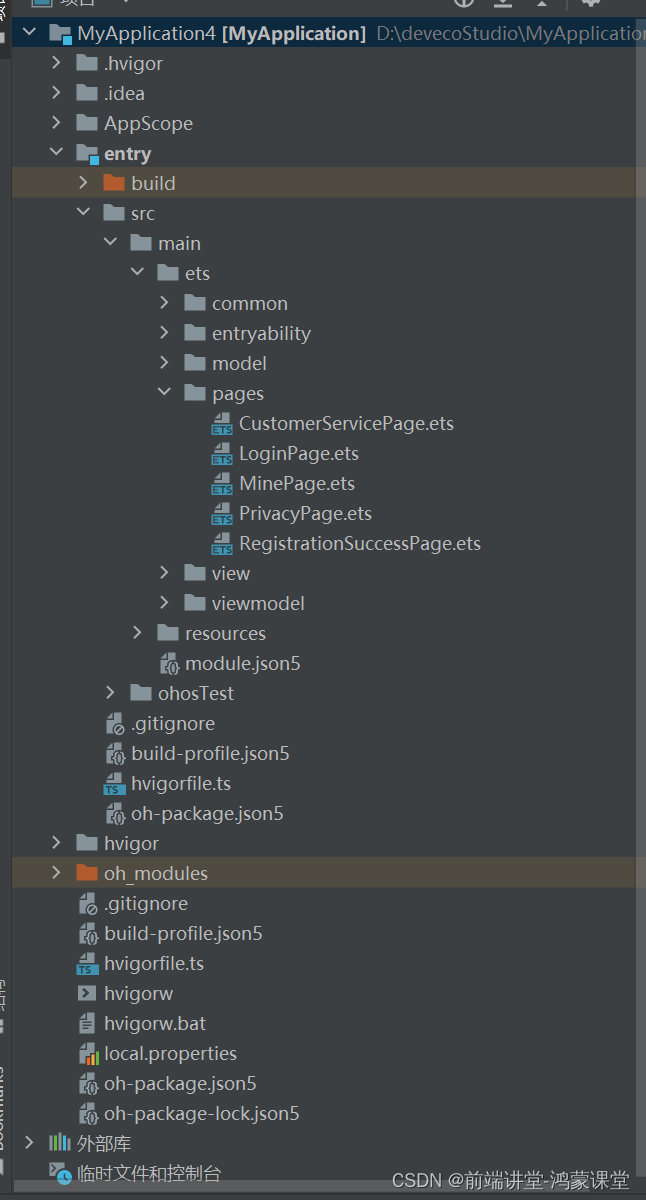
详细教程 - 从零开发 鸿蒙harmonyOS应用 第四节 (鸿蒙Stage模型 登录页面 ArkTS版 推荐使用)
在鸿蒙OS中,Ability是应用程序提供的抽象功能,可以理解为一种功能。在应用程序中,一个页面即一种能力,如登录页面,即具有登录功能的能力。以下是对鸿蒙新建项目的登录代码功能的详细解读和工作流程的描述: …...

uniapp怎么实现授权登录
在Uniapp中实现授权登录通常涉及以下几个步骤: 创建登录按钮:在页面中创建一个按钮,用于触发登录操作。 获取用户授权:当用户点击登录按钮时,调用uni.login或uni.getUserInfo等API获取用户授权。 处理授权回调&#…...

从零开始:前端架构师的基础建设和架构设计之路
文章目录 一、引言二、前端架构师的职责三、基础建设四、架构设计思想五、总结《前端架构师:基础建设与架构设计思想》编辑推荐内容简介作者简介目录获取方式 一、引言 在现代软件开发中,前端开发已经成为了一个不可或缺的部分。随着互联网的普及和移动…...
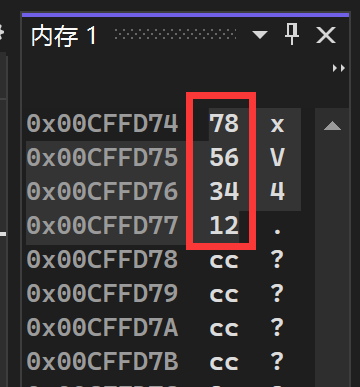
椋鸟C语言笔记#26:数据在内存中的存储(大小端字节序)、浮点数的存储(IEEE754)
萌新的学习笔记,写错了恳请斧正。 目录 大小端字节序 什么是大小端 写一个判断大小端的程序 浮点数在内存中的存储(IEEE 754规则) 引入 存储规则解释 读取规则解释 1.阶码不全为0或全为1(规格化数) 2.阶码全为…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

Q1起重机指挥理论备考要点分析
Q1起重机指挥理论备考要点分析 一、考试重点内容概述 Q1起重机指挥理论考试主要包含三大核心模块:安全技术知识(占40%)、指挥信号规范(占30%)和法规标准(占30%)。考试采用百分制,8…...

奈飞工厂官网,国内Netflix影视在线看|中文网页电脑版入口
奈飞工厂是一个专注于提供免费Netflix影视资源的在线播放平台,致力于为国内用户提供的Netflix热门影视内容。该平台的资源与Netflix官网基本同步,涵盖电影、电视剧、动漫和综艺等多个领域。奈飞工厂的界面简洁流畅,资源分类清晰,方…...
-Hive数据分析)
大数据学习(129)-Hive数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一…...
