椋鸟C语言笔记#26:数据在内存中的存储(大小端字节序)、浮点数的存储(IEEE754)
萌新的学习笔记,写错了恳请斧正。
目录
大小端字节序
什么是大小端
写一个判断大小端的程序
浮点数在内存中的存储(IEEE 754规则)
引入
存储规则解释
读取规则解释
1.阶码不全为0或全为1(规格化数)
2.阶码全为0(非规格化数)
3.阶码全为1,尾数全为0(inf)
4.阶码全为1,尾数不全为0(非数,NaN,Not a Number)
练习
1.浮点数
2.整型存储
a.下面程序的输出为
b.下面两个程序的输出为
c.下面程序的输出为
d.下面两个程序的输出为
e.下面程序的输出为(假设小端环境)
大小端字节序
什么是大小端
首先,我们要知道,整数(short、int、long、long long)在内存中以补码的形式存储,无符号整数(unsigned)在内存中以原始二进制序列存储。
当数据长度小于等于一个字节时 ,很显然计算机就直接存储在一个字节内(内存存储的基本单元是字节)。而大小端字节序,则是超过一个字节的数据在内存中存储的两种方式。
为了更清楚的理解大小端字节序,下面我们创建一个变量a:
#include <stdio.h>int main()
{int a = 0x12345678;return 0;
}我们知道int整型占4个字节,也就是说12、34、56、78会分别存储在4个字节单元中。那么,这4个字节单元在内存中是从高地址向低地址排列还是由低向高就成了一个问题。
我们把78这一头叫做数据的低位字节,12那一头叫做高位字节。那么:
- 将数据的低位字节存储在内存的高位,就叫大端存储,对应大端机器
- 将数据的低位字节存储在内存的低位,就叫小端存储,对应小端机器
下面我们在Visual Stodio(x86 Debug)环境下调试上方代码, 并打开内存窗口,观察变量a的内存空间:

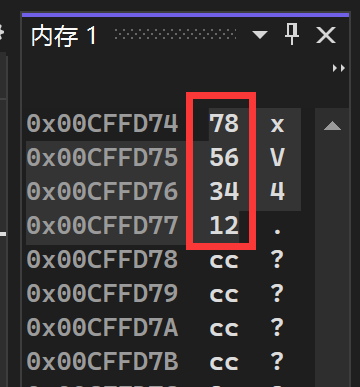
这就是将数据的低位字节(78)储存在了内存的低位,是小端存储模式。
我们常用的大多数环境(x86、x64…)都是小端结构( 有计算优势),但是仍然存在大端模式的机器(如KEIL C51)。甚至有些ARM处理器可以让硬件选择采用大端还是小端。
写一个判断大小端的程序
其实很简单,我们截取数字1在内存中的第一个字节即可。
如果输出是1就是小端机器,如果是0就是大端机器。
#include <stdio.h>int check_sys()
{int i = 1;return *(char*)&i;
}int main()
{if (check_sys())printf("该机器为小端字节序机器\n");elseprintf("该机器为大端字节序机器\n");return 0;
}这里先取a的地址、强制类型转换为char*再解引用来取出a在内存中的第一个字节。
注意:这里不能直接将a强制类型转换为char类型来读取第一个字节,因为这样永远只会截取数据最低位的字节,和大小端机器无关。
或者我们也可以用联合体的方式取第一个字节(联合体相关内容在之后的笔记):
int check_sys()
{union{int i;char c;} u;u.i = 1;return u.c;
}浮点数在内存中的存储(IEEE 754规则)
引入
浮点数包括float、double、long double等类型,可写成小数形式(3.14)或科学计数法(1.1E2)
不同浮点数的数据范围在float.h头文件中被规定
下面我们看一段代码:
#include <stdio.h>
int main()
{int n = 9;float* p = (float*)&n;printf("n的值为:%d\n", n);printf("*p的值为:%f\n", *p);*p = 9.0;printf("n的值为:%d\n", n);printf("*p的值为:%f\n", *p);return 0;
}这段代码的输出结果为:
n的值为:9
*p的值为:0.000000
n的值为:1091567616
*p的值为:9.000000明明n与*p在内存中是同一个数,为什么会出现上方的情况呢?
这与浮点数在内存中的存储有关
存储规则解释
浮点数在内存中的存储遵循IEEE 754规则,由电气与电子工程师协会(IEEE)规定
以单精度浮点数为例,我们将其分为3个部分存储在内存中(都是01组成的二进制):
- 符号位S:1位,0代表正数,1代表负数
- 阶码E:8位,就是科学计数法的指数部分加127(因为其表示精度的是-126次方到127次方,要加上127让阶码从数字1到254便于存储,因此单精度浮点数也叫余127码)(阶码0与255有特殊含义,见下方读取相关内容)
- 尾数M:23位,就是科学计数法中数字小数点后的部分
以数字5.0为例:
- 其为正数,则S=0
- 其可以表示成二进制科学计数法1.01*2^2,则尾数M为01000000000000000000000
- 其科学计数法指数为2加上127得到阶码E=129=10000001(二进制)
- 合起来就能得到数字5.0在内存中的存储:0100 0000 1010 0000 0000 0000 0000 0000
对于双精度浮点数,其规则与单精度浮点数类似,但是阶码变为11位(余1023码),尾数变为52位。总字节数由4字节变为8字节。
读取规则解释
读取时有3种情况:
1.阶码不全为0或全为1(规格化数)
读取时阶码减去127(或1023)得到指数部分,尾数加1得到数字部分
所以说单精度浮点数规格化数的指数范围是-126到127
2.阶码全为0(非规格化数)
读取时阶码加一再减去127(或1023)得到指数部分(加一使浮点数取值连续),尾数不加1,用于表示极其接近0的数字
如果尾数也全为0,则代表浮点数的±0
3.阶码全为1,尾数全为0(inf)
被判定为浮点数的无穷,正负由符号位决定,用代码inf表示
4.阶码全为1,尾数不全为0(非数,NaN,Not a Number)
用代码NaN表示,用于表示异常数据(比如某个数除以0就会返回NaN,也有可能输出IND-indeterminate不确定的)
练习
1.浮点数
这时上面浮点数存储开头的那一段代码就好理解了
首先第一部分将整型9当做浮点数输出,整型9在内存中存储为:
0000 0000 0000 0000 0000 0000 0000 1001
将其当做浮点数,则S=0,阶码E=00000000,由上面非规格化数内容我们知道这是一个趋近于0的数,所以输出了0.000000
第二部分将浮点数9.0当做整数输出,浮点数9在内存中存储为:
0100 0001 0001 0000 0000 0000 0000 0000
将其当做整型输出即补码转换为原码为:1091567616
2.整型存储
a.下面程序的输出为
#include <stdio.h>int main()
{char a = -1;signed char b = -1;unsigned char c = -1;printf("a=%d,b=%d,c=%d", a, b, c);return 0;
}就是很简单的截取,输出a=-1,b=-1,c=255
b.下面两个程序的输出为
#include <stdio.h>int main()
{char a = -128;printf("%u\n", a);return 0;
}#include <stdio.h>int main()
{char a = 128;printf("%u\n", a);return 0;
}两个程序的输出结果均为4294967168
也是简单的整型提升的问题
比如第一段程序-128的补码为1111 1111 1111 1111 1111 1111 1000 0000
截取到a为1000 0000,整型提升回1111 1111 1111 1111 1111 1111 1000 0000
其直接二进制转换十进制为4294967168
第二段等价,对于char来说127之上就循环回到-128,所以128与-128在这里没有区别
c.下面程序的输出为
#include <stdio.h>int main()
{char a[1000];int i;for (i = 0; i < 1000; i++){a[i] = -1 - i;}printf("%d", strlen(a));return 0;
}此代码输出为255
同样的,对于char类型,-128在减一就循环回到了127。所以这里就是从-1一直降到-128,在从127降到1(strlen遇到“\0”结束,其ASCII码为0,所以之后的没意义)
d.下面两个程序的输出为
#include <stdio.h>unsigned char i = 0;
int main()
{for (i = 0; i <= 255; i++){printf("hello world\n");}return 0;
}
#include <stdio.h>int main()
{unsigned int i;for (i = 9; i >= 0; i--){printf("%u\n", i);}return 0;
}这两段代码都是死循环,很简单
e.下面程序的输出为(假设小端环境)
#include <stdio.h>int main()
{int a[4] = { 1, 2, 3, 4 };int* ptr1 = (int*)(&a + 1);int* ptr2 = (int*)((int)a + 1);printf("%x,%x", ptr1[-1], *ptr2);return 0;
}其输出结果为4,2000000(有可能引发读取访问权限冲突)
很好理解,指针1减一指向数组第4个元素,指针2指向第一个元素向后偏移一位字节,也就是略过了数字1内存第一个字节又加上了数字2内存第一个字节。在小端环境下即为0x02000000
相关文章:

椋鸟C语言笔记#26:数据在内存中的存储(大小端字节序)、浮点数的存储(IEEE754)
萌新的学习笔记,写错了恳请斧正。 目录 大小端字节序 什么是大小端 写一个判断大小端的程序 浮点数在内存中的存储(IEEE 754规则) 引入 存储规则解释 读取规则解释 1.阶码不全为0或全为1(规格化数) 2.阶码全为…...
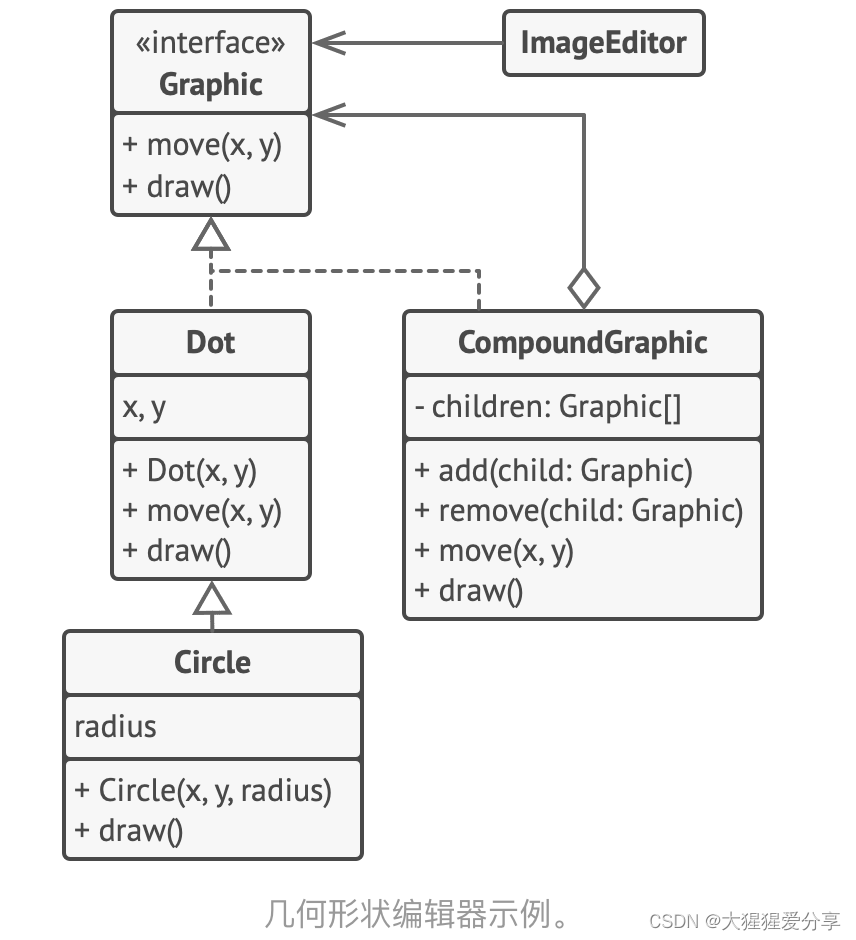
设计模式——组合模式(结构型)
引言 组合模式是一种结构型设计模式, 你可以使用它将对象组合成树状结构, 并且能像使用独立对象一样使用它们。 问题 如果应用的核心模型能用树状结构表示, 在应用中使用组合模式才有价值。 例如, 你有两类对象: …...

鸿蒙小车之多任务调度实验
说到鸿蒙我们都会想到华为mate60:遥遥领先!我们一直领先! 我们这个小车也是采用的是鸿蒙操作系统,学习鸿蒙小车,让你遥遥领先于你的同学。 文章目录 前言一、什么是任务?为什么要有任务二、任务的状态三、任…...
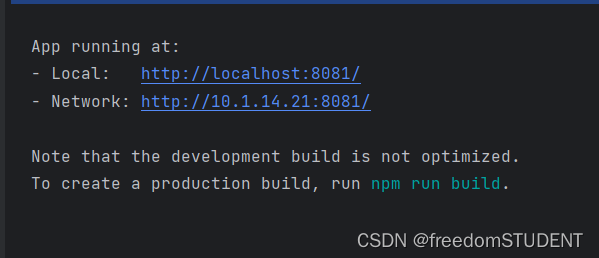
【报错栏】(vue)Module not found: Error: Can‘t resolve ‘element-ui‘ in xxx
Module not found: Error: Cant resolve element-ui in xxx 报错原因是: 未安装 element-ui 依赖 解决: npm install element-ui 运行...
seaborn库图形进行数据分析(基于tips数据集)
Seaborn 是一个基于 matplotlib 的数据可视化库,可以用来绘制各种统计图表,包括散点图、条形图、折线图、箱线图等。Seaborn 提供了一些用于美化图表的默认样式和颜色主题,使得生成的图表更具有吸引力。下面是一些 Seaborn 库的常用功能和用法…...
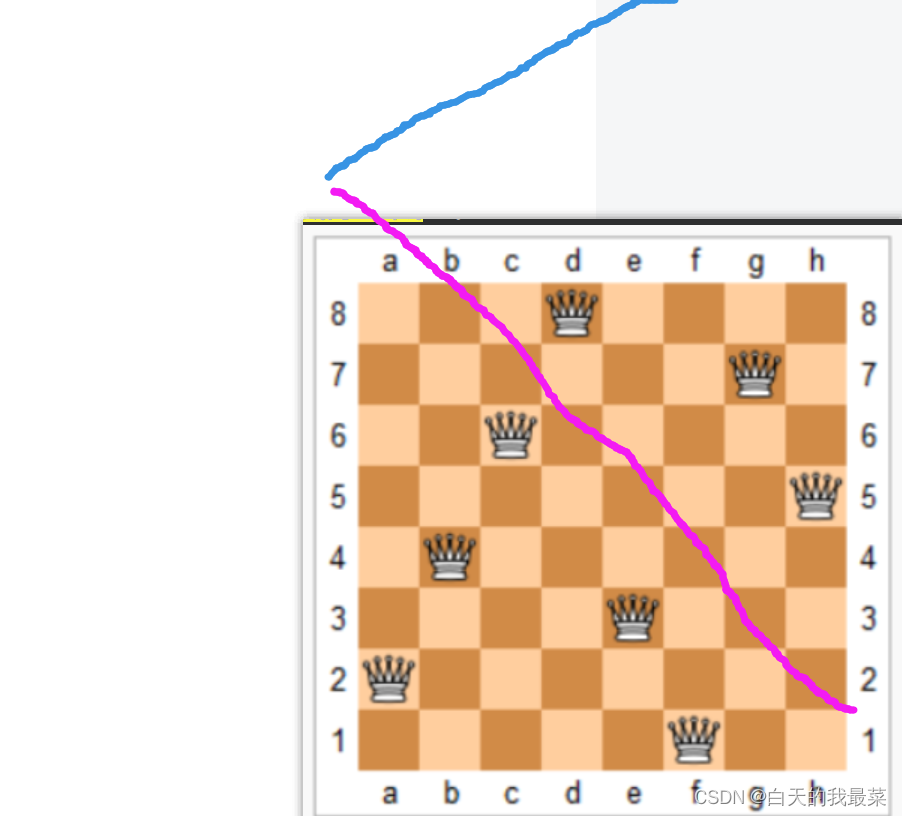
AC843. n皇后问题--60
我们只需要把蓝色的往上移动就行了 if(!col[i][j]&&!dg[ui]&&!udg[])//1y(i)向下,x(u)向右为正。yxb的by-x一定>0,y-xb的bxy可能>0,这个不考虑,只看-bxy....

Js WebSocket类,收发Json,带心跳,断线重连
如题 心跳:4秒发一次 断线:2秒后自动重连 收发:发送和返回json,处理粘包断包等情况,json字符串最大长度9999 缓存:未连接时,自动缓存100个包,当连接时会自动发出 JS代码 var MyWeb…...

VBA技术资料MF96:单字段多条件高级筛选
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...
电子取证中Chrome各版本解密Cookies、LoginData账号密码、历史记录
文章目录 1.前置知识点2.对于80.X以前版本的解密拿masterkey的几种方法方法一 直接在目标机器运行Mimikatz提取方法二 转储lsass.exe 进程从内存提取masterkey方法三 导出SAM注册表 提取user hash 解密masterkey文件(有点麻烦不太推荐)方法四 已知用户密…...

Axure元件基本介绍进阶
Axure元件基本介绍进阶 1.Axure元件基本介绍1.在 Axure 中,元件是构建原型的基本构成单元,能够帮助设计师快速创建、重复使用和管理设计元素。以下是 Axure 中元件的基本介绍:1.基本元件: 2.基本元件的使用一.【举例说明】积木&am…...

安卓11添加切换以太网动态静态方法
客户要在app中自由切换动态,静态方法,直接把系统jar-api给他搞了半天搞不定,只有在系统里给他实现一个接口,方法如下: Index: packages/apps/Settings/AndroidManifest.xml--- packages/apps/Settings/AndroidManifes…...
初级数据结构(五)——树和二叉树的概念
文中代码源文件已上传:数据结构源码 <-上一篇 初级数据结构(四)——队列 | NULL 下一篇-> 1、树结构(Tree) 1.1、树结构的特点 自然界中的树由根部开始向上生长,随机长出分支&…...
问题)
pdf读取内容缺失(漏字/文字丢失)问题
项目中遇到pdf文件漏字,由于文件涉密,不能展示,简单描述一下: 比如原pff中 姓名:张三 读取结果中:空白:张三 即:原文件说是银行出具的打款证明,银行内部设置了文件权限&a…...

c#面试基础语法——现有⼀个整数number,请写⼀个⽅法判断这个整数是否是2的N次⽅
1.number%20 取余(取模)只能判断number是不是2的倍数但不一定是2的N次方,如:6%20但是他并不是2的N次方 2.(number&(number-1))0 原理:如果number是2的N次方则表示2进制位只有一位是1。如:2 (…...
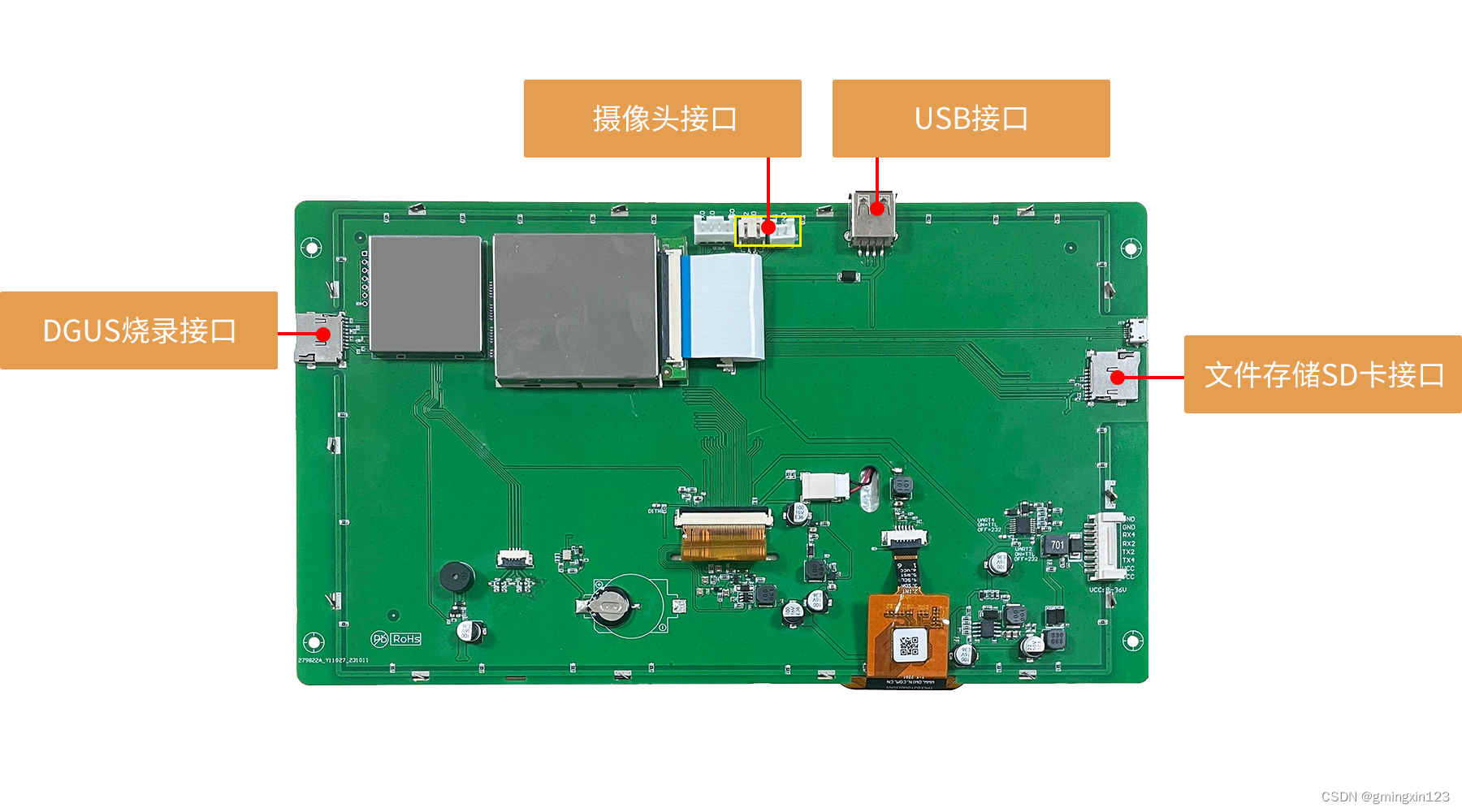
27系列DGUS智能屏发布:可实时播放高清模拟信号摄像头视频
针对高清晰度的模拟信号摄像头视频画面的显示需求,迪文特推出27系列DGUS智能屏。该系列智能屏可适配常见的AHD摄像头、CVBS摄像头,支持单路1080P高清显示、两路720P同屏显示(同一类型摄像头)。用户通过DGUS简单开发即可实现摄像头…...

YOLOv8改进 | 2023主干篇 | 替换LSKNet遥感目标检测主干 (附代码+修改教程+结构讲解)
一、本文介绍 本文给大家带来的改进内容是LSKNet(Large Kernel Selection, LK Selection),其是一种专为遥感目标检测设计的网络架构,其核心思想是动态调整其大的空间感受野,以更好地捕捉遥感场景中不同对象的范围上下…...

【工具】VUE 前端列表拖拽功能代码
【工具】VUE 前端列表拖拽功能代码 使用组件 yarn add sortablejs --save Sortable.js中文网 (sortablejs.com) 以下代码只是举个例子, 大家可以举一反三去实现各自的业务功能 <template><div><el-button type"primary" click"切换…...
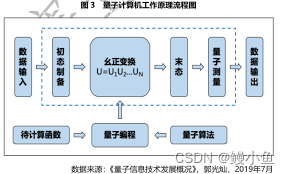
人工智能与量子计算:开启未知领域的智慧之旅
导言 人工智能与量子计算的结合是科技领域的一场创新盛宴,引领我们进入了探索未知领域的新时代。本文将深入研究人工智能与量子计算的交汇点,探讨其原理、应用以及对计算领域的深远影响。 量子计算的崛起为人工智能领域注入了新的活力,开启了…...

2023了,前端实现AI电子秤思路分析
前景小知识: 这几年ai这个话题非常火爆,笔者从事零售行业软件开发也接到了新需求,希望实现ai电子秤,老规矩,先看需求 举个栗子: 或许,你已经留意到,当你在某些大型超市超市或生鲜类…...

CSS学习
CSS学习 1. 什么是css?2.css引入方式2.1 内嵌式2.2 外联式2.3 行内式2.4 引入方式特点 3. 基础选择器3.1 标签选择器3.2 类选择器3.3 id选择器3.4 通配符选择器 4. 文字基本样式4.1 字体样式4.1.1 字体大小4.1.2 字体粗细4.1.3 倾斜4.1.4 字体4.1.5 字体font相关属性连写 4.2 …...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
