初级数据结构(五)——树和二叉树的概念
| 文中代码源文件已上传:数据结构源码 <-上一篇 初级数据结构(四)——队列 | NULL 下一篇-> |
1、树结构(Tree)
1.1、树结构的特点
自然界中的树由根部开始向上生长,随机长出分支,分支之上又可长出分支,层层递进,直至长出叶子则此分支结束。
数据结构中“树”的概念便是借鉴大自然中的树,将下图垂直镜像翻转便是如此,只是在画结构图时往往更习惯由上向下画。它从根节点开始不断长出分支,直至终端。与自然中的树不同点在于,随着数据后续插入,树结构的叶子节点也可能变为分支节点。

尤其需要注意,不同分支上的节点不可互相交织。下图中红色线条连接到其他分支的节点,这就不属于树结构:
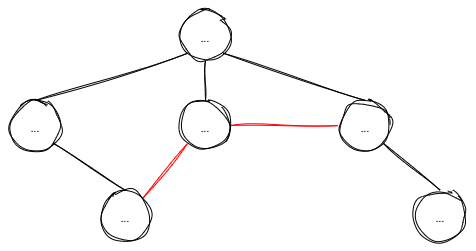
总之,树是若干个节点的有限集,有且仅有一个根节点。树的分支数量可以任意多,也可以不包含分支仅有一个根节点甚至没有节点(没有节点的树称为空树)。不同分支的节点互不相交。
1.2、常用名词
在了解树结构特点的同时,为了后续使用该结构时方便描述,还应了解几个名词。
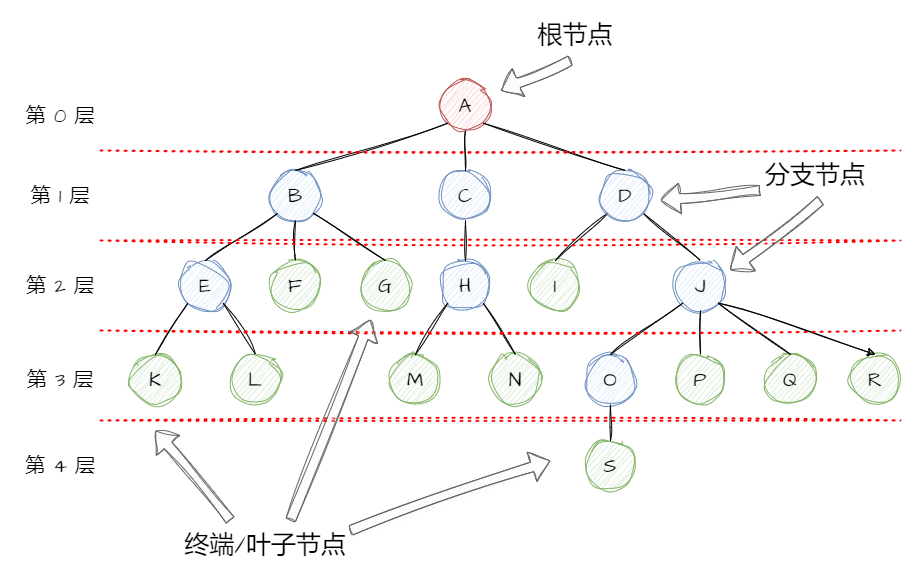
节点( Node ):树中的每一个元素称为节点,上图中每个圆圈都代表一个节点;
根节点( Root ):最初的节点称为根节点,如上图中的 A ;
子树( Subtree ):每个节点除开自身,将下一级节点当作新的根节点,从新的根节点往下所有节点的集合称为该节点的子树。上图中 B 及往后的节点是 A 的子树, F 又是 B 的子树(所以树是递归结构);
分支节点( Branch ):能够延申出其他节点的节点(度不为 0 的节点)都称作分支节点,如上图中红色及蓝色标识的节点都属于分支节点;
终端节点、叶子节点( Leaf ):不包含任何分支节点的节点(度为 0 的节点)称为终端节点或者叶子节点。上图中绿色标识的节点属于叶子节点;
度( Degree ):一个节点的分支数量叫作该节点的度,如上图 E 有两个分支 K 和 L ,所以 E 的度是 2 。一棵树中所有节点的度的最大值就是这棵树的度,上图中度最大的节点是 J , 有 4 个度,所以这棵树的度也是 4 ;
层次( Level ):从树或者子树的顶层到最底层的顺序进行排序。在这个顺序中,每个节点都被视为位于树的某个层次上。最顶上可以视为第 0 层,也可以视作第 1 层。
深度、高度(Depth):最大层次称为这棵树的深度或者高度。如图中的树从根节点开始向下,最多可经 A、D、J、O、S 这 5 个节点( 5 个层次),所以这棵树的深度为 5 ;
父节点、双亲节点( Parent ):一个节点的上一级节点称为该节点的父节点或者双亲节点。如图中 E 是 K 的父节点,A 是 B 的父节点;
子节点( Child ):一个节点的下一级节点称为该节点的子节点。图中的 O、P、Q、R 都是 J 的子节点;
兄弟节点( Sibling ):与某个节点有同一个父节点的节点称为兄弟节点。如图 E、F 都是 G 的兄弟节点;
祖先节点( Ancestry ):某个节点上数若干级直到根节点,经过的这些节点都称为祖先节点。图中 A、C、H 都是 M 或者 N 的祖先节点;
子孙节点( Descendant ):一个节点往下的所有节点都称为该节点的子孙节点。如图中 I、J、O、P、Q、R、S 都是 D 的子孙节点;
堂兄弟节点( Cousin ):与某个节点同一层次除了自身和兄弟节点外其他所有节点称为该节点的堂兄弟节点。如图中 H、I、J 都是 E、F、G 的堂兄弟节点;
森林( Forest ):若干颗互不相交的树称为森林。图中剔除 A 节点后, B、C、D 子树则构成森林;
有序树( Ordered Tree ):一棵树中各子树按照一定规律排序不可互换,则称为有序树。如图中如果将这棵树的 A、B、C …… 当作一种顺序,那么可视为有序树;
无序树( Unordered Tree ):有序树之外的树都称作无序树。
1.3、树的存储方式

如上图的树结构,如果要在代码中定义其结构体,常规能想到的是除了定义一个储存数据的成员变量外,定义若干个子节点指针。而由于子节点的数量是不确定的,因此将其定义为数组。
typedef int DATATYPE;
typedef struct Node
{DATATYPE data; //存储数据size_t childCount; //子节点个数size_t capacity; //已开辟空间大小struct Node* child[0]; //子节点指针数组
}Node;若要找到图中 1-2-2 节点则执行:
root->child[0]->child[1]->child[1];但这对于有序树这种不可随意交换节点位置的结构还好,如果是无序树,而且在经常需要交换节点的情况下, 频繁挪动数组元素显得十分不灵活。因此,还有一种储存方式,每个节点仅储存第一个子节点和其下一个兄弟节点的指针。

在结构体创建上也显得简单,而且无需每次添加数据都检查空间:
typedef int DATATYPE;
typedef struct Node
{DATATYPE data;struct Node* sibling;struct Node* child;
}Node;同样是找到 1-2-2 节点:
root->child->child->sibling->child->sibling;看似更为复杂,但整个结构在增删数据或者交换数据的操作上跟之前的结构完全不是一个量级。具体过程这里就不展开赘述,实际上就是对链表和顺序表在增删数据或者交换数据操作上的区别。
2、二叉树( Binary Tree )
2.1、节点基本形态
二叉树是一种特殊的树,每个节点的子节点不超过 2 个,它的度最大为 2 。此外,二叉树是有序树。一般其节点的结构体类型如下(二叉节点):
typedef int DATATYPE;
typedef struct Node
{DATATYPE data;struct Node* left;struct Node* right;
}还有一种三叉节点的结构体定义方式,即将父节点的地址也包含在结构体内:
typedef int DATATYPE;
typedef struct Node
{DATATYPE data;struct Node* parent;struct Node* left;struct Node* right;
}不论是二叉节点还是三叉节点,二叉树均只存在以下五种基本形态:

其中,由于二叉树是有序树,所以左分支形态和右分支形态不是同一种结构,代码的表现上也完全不同:
//空
root = NULL;
//无分支
root->left = NULL;
root->right = NULL;
//左分支
root->left = &nodeLeft;
root->right = NULL;
//右分支
root->left = NULL;
root->right = &nodeRight;
//双分支
root->left = &nodeLeft;
root->right = &nodeRight;2.2、二叉树的特殊形态
2.2.1、斜二叉树
所有节点的左或者右节点全为空的二叉树称为斜二叉树。斜二叉树每一层有且只有一个节点,节点数等于树的深度。如图。

斜二叉树可看作是一种非环状单链表,使用上也与单链表无差异。
2.2.2、完全二叉树
如果二叉树的深度为 n ,根节点处于第 0 层,除了最底层节点,其余每一层中第 L 层节点个数 都满足
,且底层最右侧节点满足其父节点的左子节点不为空,其堂兄弟节点的父节点度都为 2 ,则这类二叉树称为完全二叉树。如下图。

上面的描述可能有点过于抽象,可以观察图片,然后用另一种方式概括:
a、完全二叉树的叶子节点仅存在该二叉树的最底层和次底层;
b、最底层的叶子节点无空隙地紧密排列在左边部分,右边部分可以为空;
c、次底层的叶子节点无空隙地紧密排列在这一层右侧;
d、次底层节点的度为 1 时,该节点没有右子节点。
在同样节点数的二叉树中,不存在其他形态的二叉树深度小于完全二叉树。
2.2.3、满二叉树
满二叉树是一种特殊的完全二叉树,如图。

满二叉树的叶子节点只能出现在最下层,每个非叶子节点的分支节点度都为 2 。在所有同深度的二叉树中,满二叉树的节点最多。
2.3、二叉树规律
2.3.1、节点数规律
二叉树的叶子节点数量总是比度为 2 的节点数多 1 个。

根据上图可知,叶子节点数量增加总是伴随着度为 2 的节点数增加,而起初只有根节点时,叶子节点数为 1 ,度为 2 的节点数为 0 。因此无论如何增加节点,叶子节点数总是比度为 2 的节点数多 1 个。
2.3.2、完全二叉树标号规律
将完全二叉树节点如下图从 1 开始自左向右自上向下编号:
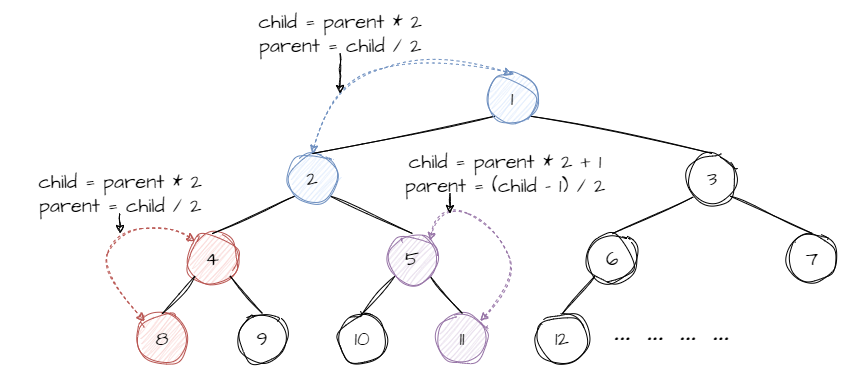
由于整型运算 1 / 2 = 0 ,因此会发现完全二叉树父子间的编号关系如下列代码:
parent = child / 2;
leftChild = parent * 2;
rightChild = parent * 2 + 1;而如果从 0 开始编号:
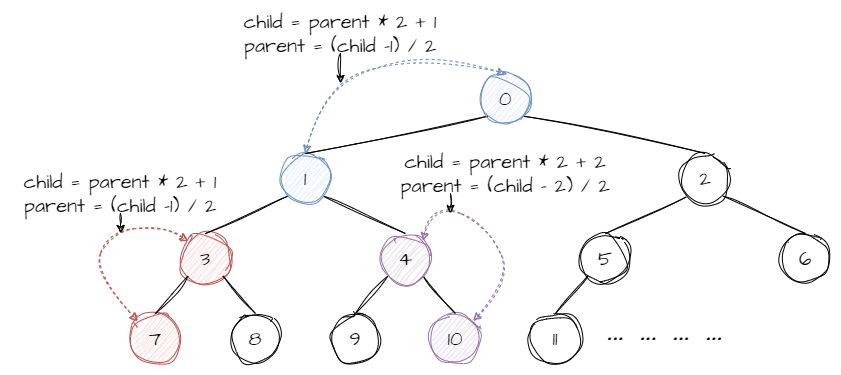
则满足以下代码:
parent = (child - 1) / 2;
leftChild = parent * 2 + 1;
rightChild = parent * 2 + 2;这一特性特别重要,在下一篇关于堆的内容中会用到。
2.3.3、完全二叉树深度
已知完全二叉树节点数为 n ,其深度为 。
根据以下代码可以计算出完全二叉树的深度:
#include <math.h>
#include <stdio.h>int main()
{int nodeCount;scanf("%d", &nodeCount);int depth = (int)(log(nodeCount) / log(2)) + 1;printf("Depth = %d\n", depth);return 0;
}相关文章:
初级数据结构(五)——树和二叉树的概念
文中代码源文件已上传:数据结构源码 <-上一篇 初级数据结构(四)——队列 | NULL 下一篇-> 1、树结构(Tree) 1.1、树结构的特点 自然界中的树由根部开始向上生长,随机长出分支&…...
问题)
pdf读取内容缺失(漏字/文字丢失)问题
项目中遇到pdf文件漏字,由于文件涉密,不能展示,简单描述一下: 比如原pff中 姓名:张三 读取结果中:空白:张三 即:原文件说是银行出具的打款证明,银行内部设置了文件权限&a…...

c#面试基础语法——现有⼀个整数number,请写⼀个⽅法判断这个整数是否是2的N次⽅
1.number%20 取余(取模)只能判断number是不是2的倍数但不一定是2的N次方,如:6%20但是他并不是2的N次方 2.(number&(number-1))0 原理:如果number是2的N次方则表示2进制位只有一位是1。如:2 (…...
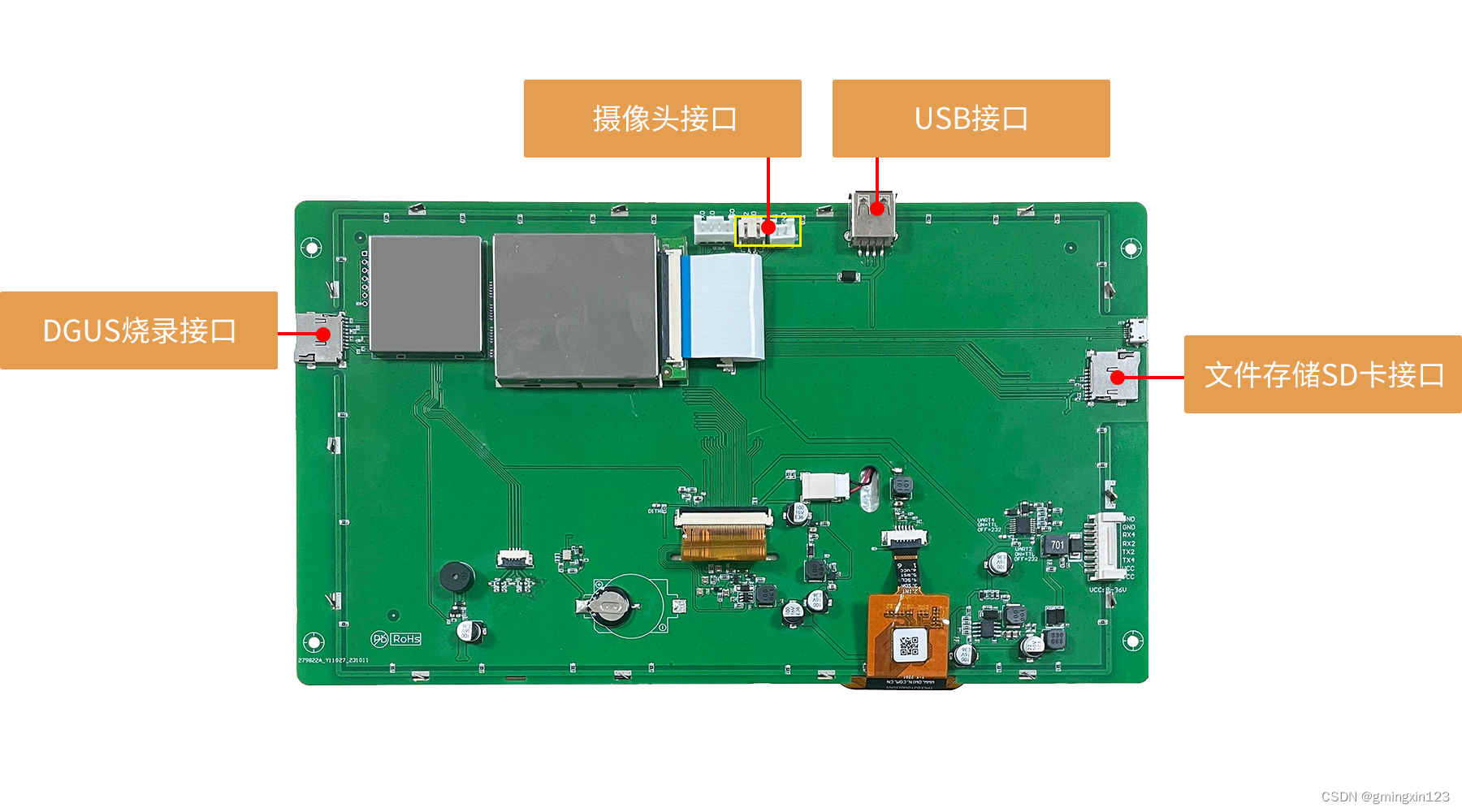
27系列DGUS智能屏发布:可实时播放高清模拟信号摄像头视频
针对高清晰度的模拟信号摄像头视频画面的显示需求,迪文特推出27系列DGUS智能屏。该系列智能屏可适配常见的AHD摄像头、CVBS摄像头,支持单路1080P高清显示、两路720P同屏显示(同一类型摄像头)。用户通过DGUS简单开发即可实现摄像头…...

YOLOv8改进 | 2023主干篇 | 替换LSKNet遥感目标检测主干 (附代码+修改教程+结构讲解)
一、本文介绍 本文给大家带来的改进内容是LSKNet(Large Kernel Selection, LK Selection),其是一种专为遥感目标检测设计的网络架构,其核心思想是动态调整其大的空间感受野,以更好地捕捉遥感场景中不同对象的范围上下…...

【工具】VUE 前端列表拖拽功能代码
【工具】VUE 前端列表拖拽功能代码 使用组件 yarn add sortablejs --save Sortable.js中文网 (sortablejs.com) 以下代码只是举个例子, 大家可以举一反三去实现各自的业务功能 <template><div><el-button type"primary" click"切换…...
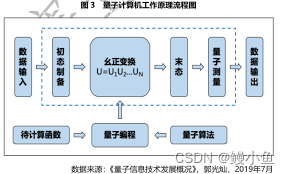
人工智能与量子计算:开启未知领域的智慧之旅
导言 人工智能与量子计算的结合是科技领域的一场创新盛宴,引领我们进入了探索未知领域的新时代。本文将深入研究人工智能与量子计算的交汇点,探讨其原理、应用以及对计算领域的深远影响。 量子计算的崛起为人工智能领域注入了新的活力,开启了…...

2023了,前端实现AI电子秤思路分析
前景小知识: 这几年ai这个话题非常火爆,笔者从事零售行业软件开发也接到了新需求,希望实现ai电子秤,老规矩,先看需求 举个栗子: 或许,你已经留意到,当你在某些大型超市超市或生鲜类…...

CSS学习
CSS学习 1. 什么是css?2.css引入方式2.1 内嵌式2.2 外联式2.3 行内式2.4 引入方式特点 3. 基础选择器3.1 标签选择器3.2 类选择器3.3 id选择器3.4 通配符选择器 4. 文字基本样式4.1 字体样式4.1.1 字体大小4.1.2 字体粗细4.1.3 倾斜4.1.4 字体4.1.5 字体font相关属性连写 4.2 …...

Flask基本用法:一个HelloWorld,搭建服务、发起请求
目录 1、简介 2、安装 3、Flask使用示例 参考 1、简介 官网文档 Flask是一个轻量的web服务框架,我们可以利用它快速搭建一个服务,对外提供接口,其他人可以轻松调用我们的服务。这对算法工程师来说比较关键,我们通常不擅长搞开发…...
Tomcat-安装部署(源码包安装)
一、简介 Tomcat 是由 Apache 开发的一个 Servlet 容器,实现了对 Servlet 和 JSP 的支持,并提供了作为Web服务器的一些特有功能,如Tomcat管理和控制平台、安全域管理和Tomcat阀等。 简单来说,Tomcat是一个WEB应用程序的托管平台…...

【Hadoop_06】MapReduce的概述与wc案例
1、MapReduce概述1.1 MapReduce定义1.2 MapReduce优点1.3 MapReduce缺点1.4 MapReduce核心思想1.5 MapReduce进程1.6 常用数据序列化类型1.7 源码与MapReduce编程规范 2、WordCount案例实操2.1 本地测试2.2 提交到集群测试 1、MapReduce概述 1.1 MapReduce定义 MapReduce是一…...

Qt点击子窗口时父窗口标题栏高亮设计思路
父窗口调用findChildren得到其子孙窗口的列表,列表元素统一为QWidget*,遍历列表元素,每个元素调用installEventFilter,过滤QEvent::FocusIn和QEvent::FocusOut事件,做相应处理即可: QWidget* parent; QLis…...
掌握iText:轻松处理PDF文档-高级篇-添加水印
前言 iText作为一个功能强大、灵活且广泛应用的PDF处理工具,在实际项目中发挥着重要作用。通过这些文章,读者可以深入了解如何利用iText进行PDF的创建、编辑、加密和提取文本等操作,为日常开发工作提供了宝贵的参考和指导。 掌握iText&…...
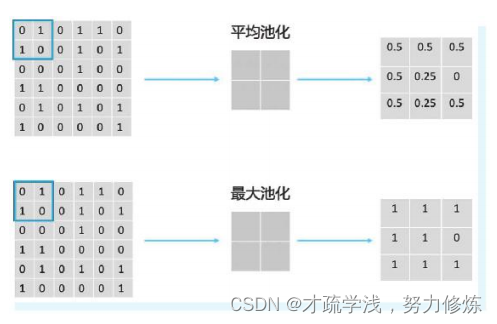
深度学习基本概念
1.全连接层 全连接层就是该层的所有节点与输入节点全部相连,如图所 示。假设输入节点为X1, X 2, X 3,输出节点为 Y 1, Y 2, Y 3, Y 4。令 矩阵 W 代表全连接层的权重, W 12也就代表 …...

2023年最详细的:本地Linux服务器安装宝塔面板,并内网穿透实现公网远程登录
📚📚 🏅我是默,一个在CSDN分享笔记的博主。📚📚 🌟在这里,我要推荐给大家我的专栏《Linux》。🎯🎯 🚀无论你是编程小白,还是有一…...

基于ssm金旗帜文化培训学校网站的设计与开发论文
摘 要 互联网发展至今,无论是其理论还是技术都已经成熟,而且它广泛参与在社会中的方方面面。它让信息都可以通过网络传播,搭配信息管理工具可以很好地为人们提供服务。针对培训学校展示信息管理混乱,出错率高,信息安全…...

【Java】猜数字小游戏
规则 游戏开始随机生成4位数字符串,每个数字从0到9各不相同,比如0123玩家10次猜数机会,输入4位数字符串,每个数字从0到9各不相同游戏判断玩家输入与所猜谜底数,给出结果nAnB,A表示位置和数字都猜对的个数&…...
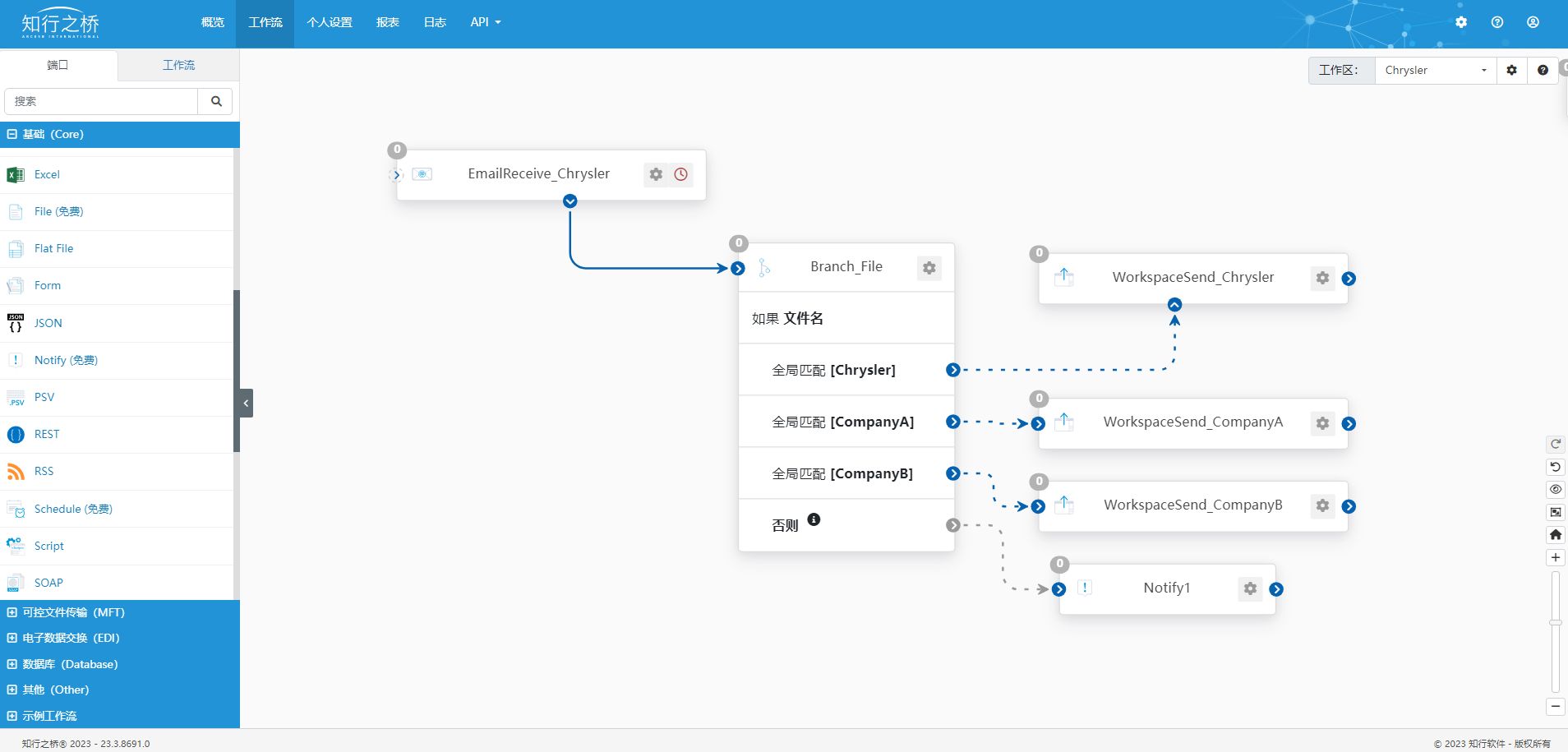
汽车EDI:Chrysler EDI项目案例
菲亚特克莱斯勒汽车Fiat Chrysler Automobiles(FCA)是一家全球性汽车制造商,主营产品包括轿车、SUV、皮卡车、商用车和豪华车等多种车型。其旗下品牌包括菲亚特、克莱斯勒、道奇、Jeep、Ram、阿尔法罗密欧和玛莎拉蒂等。 Chrysler通过EDI来优化订单处理、交付通知、…...
Locust:可能是一款最被低估的压测工具
01、Locust介绍 开源性能测试工具https://www.locust.io/,基于Python的性能压测工具,使用Python代码来定义用户行为,模拟百万计的并发用户访问。每个测试用户的行为由您定义,并且通过Web UI实时监控聚集过程。 压力发生器作为性能…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
