人工智能与量子计算:开启未知领域的智慧之旅
导言
人工智能与量子计算的结合是科技领域的一场创新盛宴,引领我们进入了探索未知领域的新时代。本文将深入研究人工智能与量子计算的交汇点,探讨其原理、应用以及对计算领域的深远影响。
量子计算的崛起为人工智能领域注入了新的活力,开启了一场变革性的探索之旅。本文将深入探讨量子计算对当前人工智能领域的影响,以及未来的挑战和机遇。
1. 简介
人工智能和量子计算作为两大前沿技术的结合,为解决传统计算面临的难题提供了全新的可能性。
2. 技术原理
- 量子比特: 量子计算利用量子比特的叠加和纠缠特性,以同时处理多种状态的方式进行计算。
- 量子神经网络: 将深度学习与量子计算相结合,构建更为强大的神经网络模型。
- 量子态: 利用量子态的独特性质,实现对大规模数据的高效处理。
- 优化算法: 量子计算可以显著提高优化问题的求解效率,对于人工智能中的模型参数优化具有重要意义。
- 机器学习: 利用量子计算进行更复杂、更高效的机器学习模型训练,加速人工智能算法的学习过程。
- 模拟与模型: 量子计算在模拟复杂系统、提升人工智能模型的表达能力上具备独特优势。
3. 应用领域
- 优化问题: 量子计算在解决复杂的优化问题上具有天然的优势,如物流优化、能源分配等。
- 化学模拟: 模拟分子的结构和性质,对新材料和药物的研发具有重要意义。
- 人工智能算法优化: 利用量子计算提高机器学习和深度学习算法的训练效率。
- 硬件稳定性: 提高量子比特的稳定性和减少错误率是当前亟待解决的难题,需要加强硬件研究。
- 算法优化: 针对量子计算架构,需要开发更适应量子计算方式的新型算法。
- 标准化: 制定量子计算的标准,以促进其在人工智能领域的广泛应用。
4. 挑战与未来展望
- 错误率与稳定性: 提高量子比特的稳定性和降低错误率是目前面临的主要挑战。
- 硬件发展: 量子计算硬件的发展对实现实用性至关重要。
- 标准化与应用: 制定量子计算的标准,推动其广泛应用于各行业。
- 深度学习革新: 量子计算有望推动深度学习的革新,使其更好地处理复杂问题。
- 新型算法探索: 量子计算将激发新型算法的探索,为人工智能算法提供更多可能性。
- 科研突破: 量子计算的不断发展将催生更多颠覆性的科学研究和技术突破。
5. 结语
人工智能量子计算的结合既是科技发展的必然趋势,也是打开计算科学未知领域的一把金钥匙。在不断攀登技术高峰的过程中,我们期待这一融合将为人类带来更深层次的认知和探索。
量子计算与人工智能的结合为科技领域带来了前所未有的机遇,同时也面临着前所未有的挑战。在共同努力下,我们有望见证量子计算引领人工智能进入全新的发展时代。

延伸阅读
- 量子计算对人工智能的影响
- 量子计算在生物信息学中的应用
- 人工智能量子计算的伦理与法律问题
完结撒花
在人工智能与量子计算的奇妙交汇中,我们站在科技发展的巅峰,眺望着未知的辽阔。让我们携手迎接这一前沿科技带来的全新时代,共同创造更为智慧的未来。
在量子计算的光芒下,人工智能焕发出崭新的活力。让我们迎接这场科技变革,共同努力创造一个更为智能、更为进步的未来。
相关文章:

人工智能与量子计算:开启未知领域的智慧之旅
导言 人工智能与量子计算的结合是科技领域的一场创新盛宴,引领我们进入了探索未知领域的新时代。本文将深入研究人工智能与量子计算的交汇点,探讨其原理、应用以及对计算领域的深远影响。 量子计算的崛起为人工智能领域注入了新的活力,开启了…...

2023了,前端实现AI电子秤思路分析
前景小知识: 这几年ai这个话题非常火爆,笔者从事零售行业软件开发也接到了新需求,希望实现ai电子秤,老规矩,先看需求 举个栗子: 或许,你已经留意到,当你在某些大型超市超市或生鲜类…...

CSS学习
CSS学习 1. 什么是css?2.css引入方式2.1 内嵌式2.2 外联式2.3 行内式2.4 引入方式特点 3. 基础选择器3.1 标签选择器3.2 类选择器3.3 id选择器3.4 通配符选择器 4. 文字基本样式4.1 字体样式4.1.1 字体大小4.1.2 字体粗细4.1.3 倾斜4.1.4 字体4.1.5 字体font相关属性连写 4.2 …...

Flask基本用法:一个HelloWorld,搭建服务、发起请求
目录 1、简介 2、安装 3、Flask使用示例 参考 1、简介 官网文档 Flask是一个轻量的web服务框架,我们可以利用它快速搭建一个服务,对外提供接口,其他人可以轻松调用我们的服务。这对算法工程师来说比较关键,我们通常不擅长搞开发…...
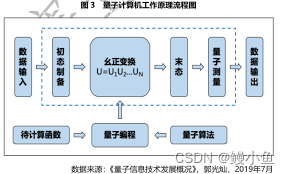
Tomcat-安装部署(源码包安装)
一、简介 Tomcat 是由 Apache 开发的一个 Servlet 容器,实现了对 Servlet 和 JSP 的支持,并提供了作为Web服务器的一些特有功能,如Tomcat管理和控制平台、安全域管理和Tomcat阀等。 简单来说,Tomcat是一个WEB应用程序的托管平台…...

【Hadoop_06】MapReduce的概述与wc案例
1、MapReduce概述1.1 MapReduce定义1.2 MapReduce优点1.3 MapReduce缺点1.4 MapReduce核心思想1.5 MapReduce进程1.6 常用数据序列化类型1.7 源码与MapReduce编程规范 2、WordCount案例实操2.1 本地测试2.2 提交到集群测试 1、MapReduce概述 1.1 MapReduce定义 MapReduce是一…...

Qt点击子窗口时父窗口标题栏高亮设计思路
父窗口调用findChildren得到其子孙窗口的列表,列表元素统一为QWidget*,遍历列表元素,每个元素调用installEventFilter,过滤QEvent::FocusIn和QEvent::FocusOut事件,做相应处理即可: QWidget* parent; QLis…...
掌握iText:轻松处理PDF文档-高级篇-添加水印
前言 iText作为一个功能强大、灵活且广泛应用的PDF处理工具,在实际项目中发挥着重要作用。通过这些文章,读者可以深入了解如何利用iText进行PDF的创建、编辑、加密和提取文本等操作,为日常开发工作提供了宝贵的参考和指导。 掌握iText&…...
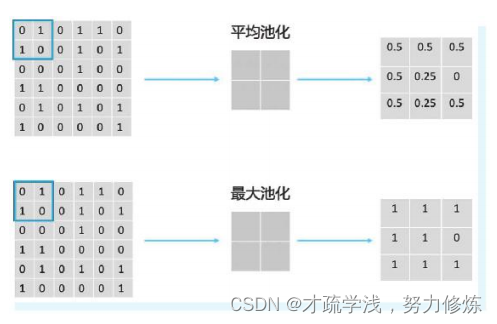
深度学习基本概念
1.全连接层 全连接层就是该层的所有节点与输入节点全部相连,如图所 示。假设输入节点为X1, X 2, X 3,输出节点为 Y 1, Y 2, Y 3, Y 4。令 矩阵 W 代表全连接层的权重, W 12也就代表 …...

2023年最详细的:本地Linux服务器安装宝塔面板,并内网穿透实现公网远程登录
📚📚 🏅我是默,一个在CSDN分享笔记的博主。📚📚 🌟在这里,我要推荐给大家我的专栏《Linux》。🎯🎯 🚀无论你是编程小白,还是有一…...

基于ssm金旗帜文化培训学校网站的设计与开发论文
摘 要 互联网发展至今,无论是其理论还是技术都已经成熟,而且它广泛参与在社会中的方方面面。它让信息都可以通过网络传播,搭配信息管理工具可以很好地为人们提供服务。针对培训学校展示信息管理混乱,出错率高,信息安全…...

【Java】猜数字小游戏
规则 游戏开始随机生成4位数字符串,每个数字从0到9各不相同,比如0123玩家10次猜数机会,输入4位数字符串,每个数字从0到9各不相同游戏判断玩家输入与所猜谜底数,给出结果nAnB,A表示位置和数字都猜对的个数&…...
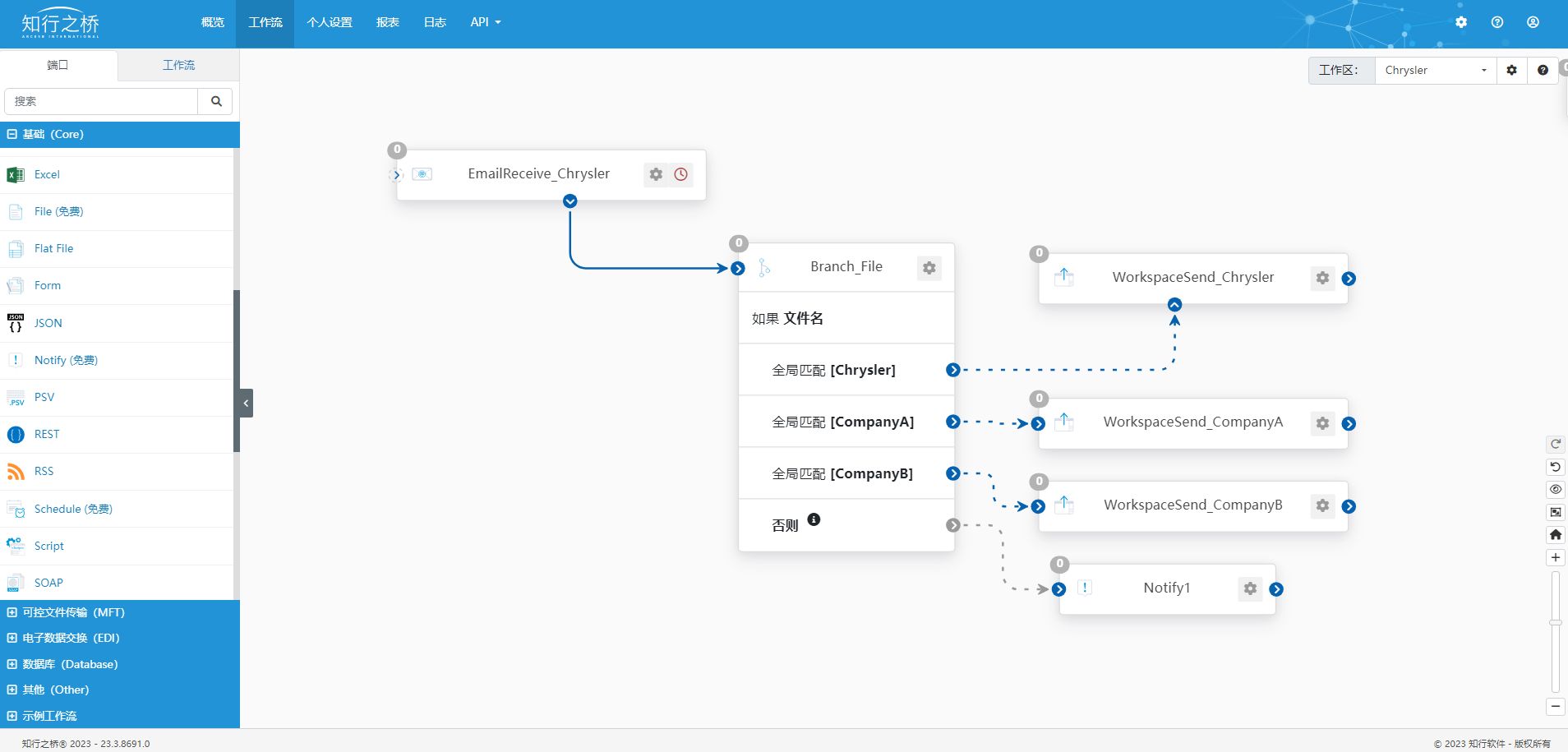
汽车EDI:Chrysler EDI项目案例
菲亚特克莱斯勒汽车Fiat Chrysler Automobiles(FCA)是一家全球性汽车制造商,主营产品包括轿车、SUV、皮卡车、商用车和豪华车等多种车型。其旗下品牌包括菲亚特、克莱斯勒、道奇、Jeep、Ram、阿尔法罗密欧和玛莎拉蒂等。 Chrysler通过EDI来优化订单处理、交付通知、…...
Locust:可能是一款最被低估的压测工具
01、Locust介绍 开源性能测试工具https://www.locust.io/,基于Python的性能压测工具,使用Python代码来定义用户行为,模拟百万计的并发用户访问。每个测试用户的行为由您定义,并且通过Web UI实时监控聚集过程。 压力发生器作为性能…...
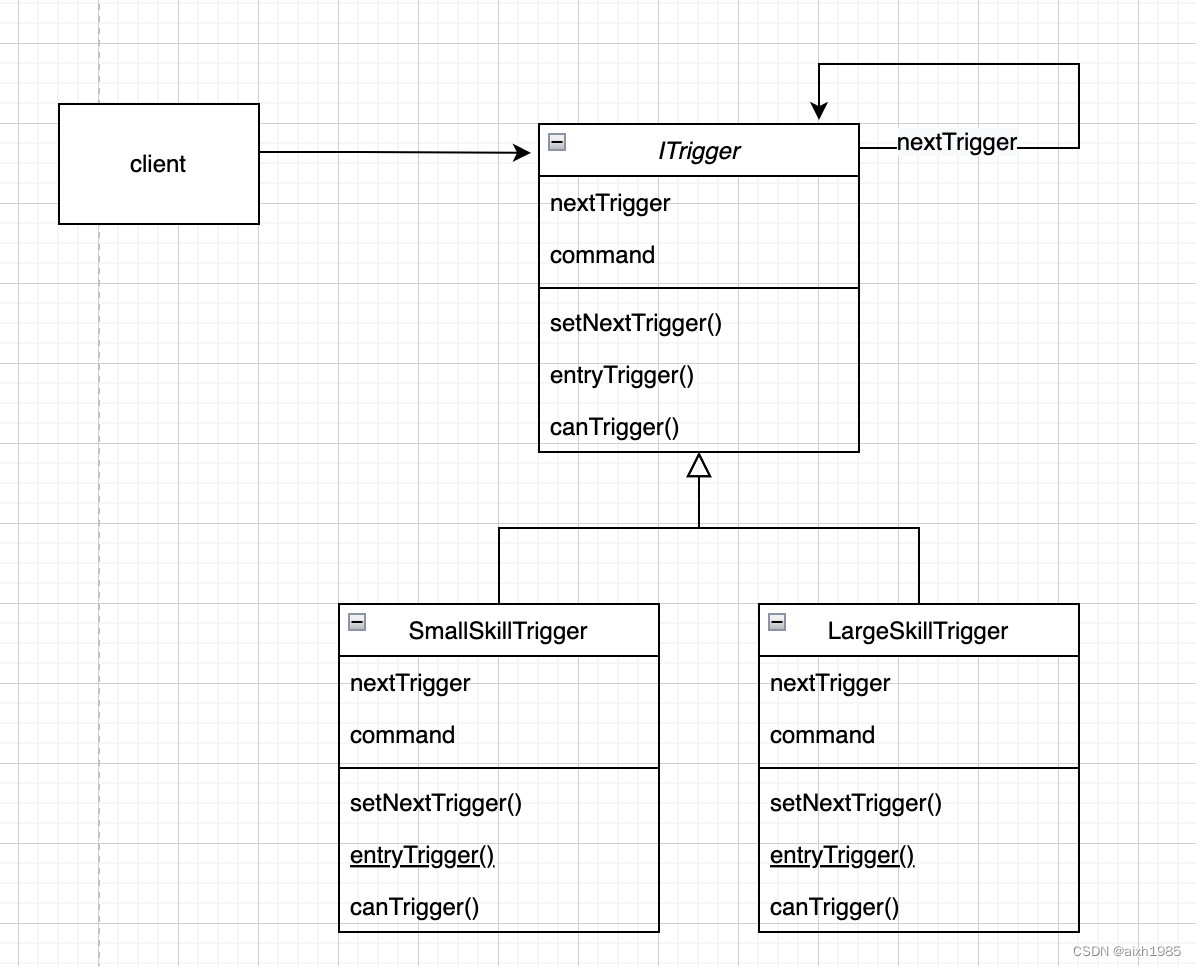
用23种设计模式打造一个cocos creator的游戏框架----(十八)责任链模式
1、模式标准 模式名称:责任链模式 模式分类:行为型 模式意图:使多个对象都有机会处理请求,从而避免请求的发送者和接收者之间的耦合关系。将这些对象连成一条链,并沿着这条链传递该请求,直到有一个对象处…...
——第9天:风控建模中为什么需要特征工程?)
100天精通风控建模(原理+Python实现)——第9天:风控建模中为什么需要特征工程?
风控模型已在各大银行和公司都实际运用于业务,用于营销和风险控制等。本文以视频的形式阐述风控建模中为什么需要特征工程。并提供风控建模原理和Python实现文章清单。 之前已经阐述了100天精通风控建模(原理+Python实现)——第1天:什么是风控建模? 100天精通风控…...

【PHP】计算某个特定时间戳距离现在的天数
在PHP中,你可以使用time()函数获取当前时间的时间戳,然后将它与你想要计算的过去或未来的时间戳进行比较。为了得到相差的天数,你需要先用两个时间戳相减得到秒数差,然后再除以一天的总秒数(通常是86400秒)…...
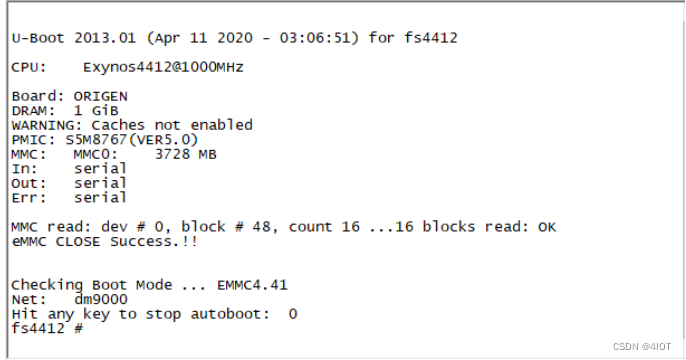
lv12 uboot移植深化 9
u-boot-2013.01移植 【实验目的】 了解u-boot 的代码结构及移植的基本方法 【实验环境】 ubuntu 14.04发行版FS4412实验平台交叉编译工具arm-none-linux-gnueabi- 【注意事项】 实验步骤中以“$”开头的命令表示在 ubuntu 环境下执行 【实验步骤】 1 建立自己的平台 1.…...

大数据与深度挖掘:如何在数字营销中与研究互动
数字营销最吸引人的部分之一是对数据的内在关注。 如果一种策略往往有积极的数据,那么它就更容易采用。同样,如果一种策略尚未得到证实,则很难获得支持进行测试。 数字营销人员建立数据信心的主要方式是通过研究。这些研究通常分为两类&…...

xtu oj 1327 字符矩阵
按照示例的规律输出字符矩阵。 比如输入字母D时,输出字符矩阵如下 ABCDCBA BBCDCBB CCCDCCC DDDDDDD CCCDCCC BBCDCBB ABCDCBA字符矩阵行首、尾都无空格。 输入 每行一个大写英文字母,如果字符为#,表示输入结束,不需要处理。 …...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
