D33|动态规划!启程!
1.动态规划五部曲:
1)确定dp数组(dp table)以及下标的含义
2)确定递推公式
3)dp数组如何初始化
4)确定遍历顺序
5)举例推导dp数组
2.动态规划应该如何debug
找问题的最好方式就是把dp数组打印出来,看看究竟是不是按照自己思路推导的!
509.斐波那契数
初始思路:
class Solution {public int fib(int n) {if(n==0){return 0;}int[] dp = new int[n+1];dp[0] = 0;dp[1] = 1;for(int i = 2;i<n+1;i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
}题解复盘:
题解更加清晰,首先按照动态规划五部曲进行分析:
1)确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
2)确定递推公式
状态转移方程 dp[i] = dp[i - 1] + dp[i - 2]
3)dp数组如何初始化
dp[0] = 0;
dp[1] = 1;4)确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的。
5)举例推导dp数组
0 1 1 2 3 5 8 13 21 34 55
压缩空间版本的题解:
class Solution {public int fib(int n) {if (n < 2) return n;int a = 0, b = 1, c = 0;for (int i = 1; i < n; i++) {c = a + b;a = b;b = c;}return c;}
}70.爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
初始思路:
1)确定dp数组以及下标的含义:
dp[i]的定义为:表示爬到第i个台阶不同方法的数量。
2)确定递推公式:
dp[i] = dp[i - 1] + dp[i - 2]
3)dp数组如何初始化
dp[1] = 1;爬一层台阶只有一种方法
dp[2] = 2;爬两层台阶可以一次爬两层也可以爬两个一层。
4)确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的。
5)举例推导dp数组
1,2,3,5,8,13,21,34
class Solution {public int climbStairs(int n) {if(n<=2){return n;}int a = 1;int b = 2;int c = 0;for(int i = 3;i<n+1;i++){c = a + b;a = b;b = c;}return c;}
}746. 使用最小花费爬楼梯
初始思路:
这道题目就是在不同的爬楼梯方案中,挑选出来最小花费的爬楼梯方案。
唯一需要斟酌的地方就是我究竟是让其从第0阶台阶开始攀爬,还是从第1阶台阶开始攀爬。
1)确定dp数组以及下标的含义:
dp[i]的定义为:表示爬到第i个台阶所需要的最小花费。
2)确定递推公式:
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
3) dp数组如何初始化
dp[0] = 0;dp[1] = 0;dp[2] = min(dp[0]+cost[0],cost[1]+dp[1]);
4) 确定遍历顺序
由前到后
5)举例推导dp数组

0,0,10,15
class Solution {public int minCostClimbingStairs(int[] cost) {int[] dp = new int[cost.length+1];dp[0] = 0;dp[1] = 0;for(int i = 2;i<=cost.length;i++){dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.length];}
}题解复盘:
基本一致
相关文章:

D33|动态规划!启程!
1.动态规划五部曲: 1)确定dp数组(dp table)以及下标的含义 2)确定递推公式 3)dp数组如何初始化 4)确定遍历顺序 5)举例推导dp数组 2.动态规划应该如何debug 找问题的最好方式就是把…...
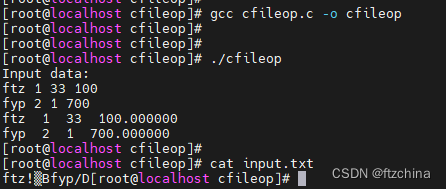
C语言----文件操作(二)
在上一篇文章中我们简单介绍了在C语言中文件是什么以及文件的打开和关闭操作,在实际工作中,我们不仅仅是要打开和关闭文件,二是需要对文件进行增删改写。本文将详细介绍如果对文件进行安全读写。 一,以字符形式读写文件ÿ…...

oracle 10046事件跟踪
10046事件是一个很好的排查sql语句执行缓慢的内部事件,具体设置方式如下: 根据10046事件跟踪SQL语句 1、 alter session set events 10046 trace name context forever,level 12; 2、执行SQL语句 3、关闭10046事件 alter session set events 10046 trace…...
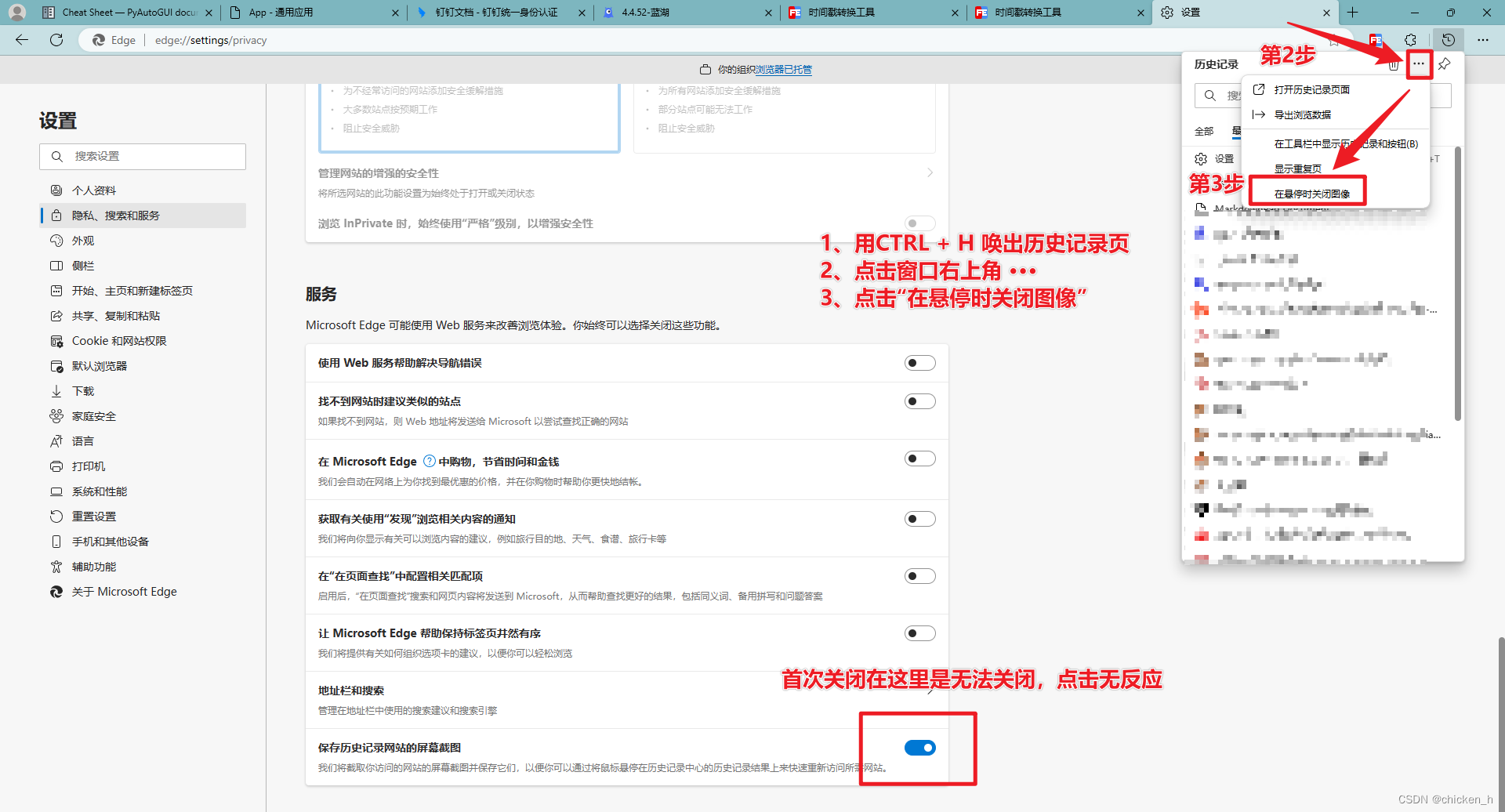
微软自带浏览器Edge,无法关闭“保存历史记录网站的屏幕截图”解决方案
微软自带浏览器Edge,无法关闭“保存历史记录网站的屏幕截图”解决方案 吐槽1:Windows自带的Chrome内核版本的浏览器Microsofg Edge刚发布时可谓一股清流,启动速度快,占用内存较小,相信很多人也开始抛弃正代Chrome&…...

讲座 | 颠覆传统摄像方式乃至计算机视觉的“脉冲视觉”
传统相机拍摄视频时其实是以一定帧率进行采样,视频其实还是一串图片的集合,因此低帧率时会觉得视频卡,拍摄高速运动物体时会有运动模糊等等问题。然而你能想象这一切都可以被“脉冲视觉”这一前沿技术改变吗? 今天下午听了北京大学…...
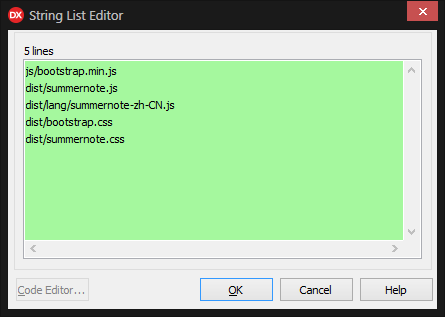
uniGUI学习之UniHTMLMemo1富文本编辑器
1]系统自带的富文本编辑器 2]jQueryBootstarp富文本编辑器插件summernote.js 1]系统自带的富文本编辑器 1、末尾增加<p> 2、增加字体 3、解决滚屏问题 4、输入长度限制问题 5、显示 并 编辑 HTML源代码(主要是图片处理) 1、末尾增加<p> UniHTMLMemo1.Lines…...
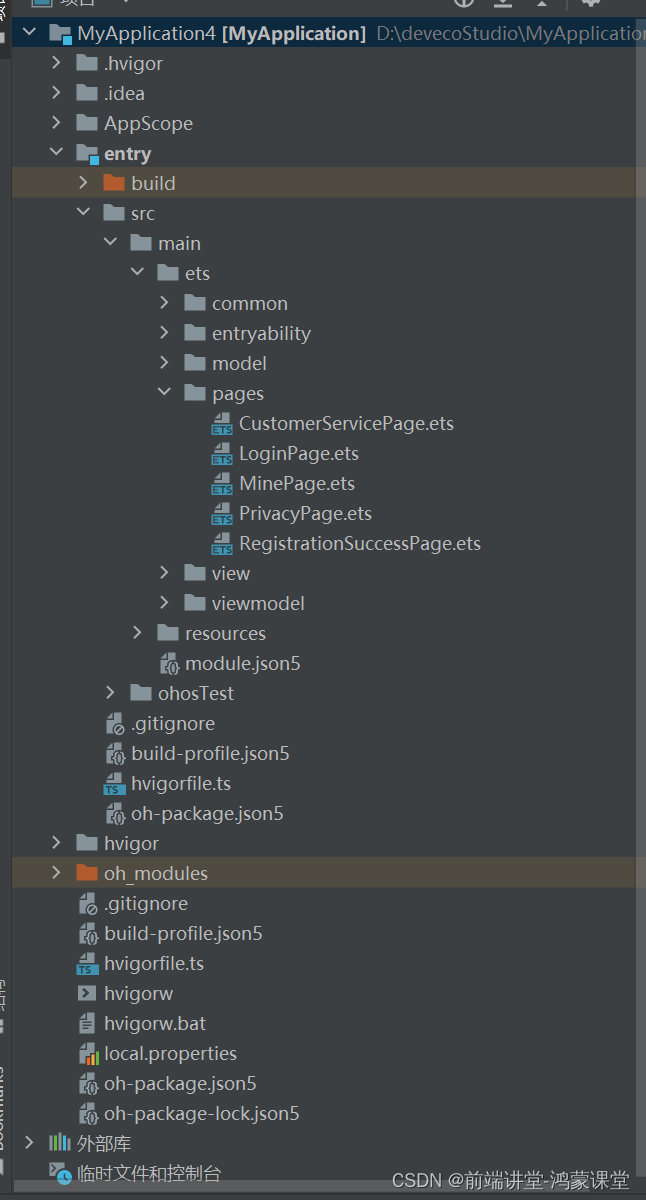
详细教程 - 从零开发 鸿蒙harmonyOS应用 第四节 (鸿蒙Stage模型 登录页面 ArkTS版 推荐使用)
在鸿蒙OS中,Ability是应用程序提供的抽象功能,可以理解为一种功能。在应用程序中,一个页面即一种能力,如登录页面,即具有登录功能的能力。以下是对鸿蒙新建项目的登录代码功能的详细解读和工作流程的描述: …...

uniapp怎么实现授权登录
在Uniapp中实现授权登录通常涉及以下几个步骤: 创建登录按钮:在页面中创建一个按钮,用于触发登录操作。 获取用户授权:当用户点击登录按钮时,调用uni.login或uni.getUserInfo等API获取用户授权。 处理授权回调&#…...

从零开始:前端架构师的基础建设和架构设计之路
文章目录 一、引言二、前端架构师的职责三、基础建设四、架构设计思想五、总结《前端架构师:基础建设与架构设计思想》编辑推荐内容简介作者简介目录获取方式 一、引言 在现代软件开发中,前端开发已经成为了一个不可或缺的部分。随着互联网的普及和移动…...
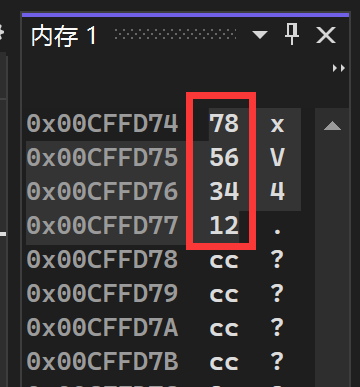
椋鸟C语言笔记#26:数据在内存中的存储(大小端字节序)、浮点数的存储(IEEE754)
萌新的学习笔记,写错了恳请斧正。 目录 大小端字节序 什么是大小端 写一个判断大小端的程序 浮点数在内存中的存储(IEEE 754规则) 引入 存储规则解释 读取规则解释 1.阶码不全为0或全为1(规格化数) 2.阶码全为…...
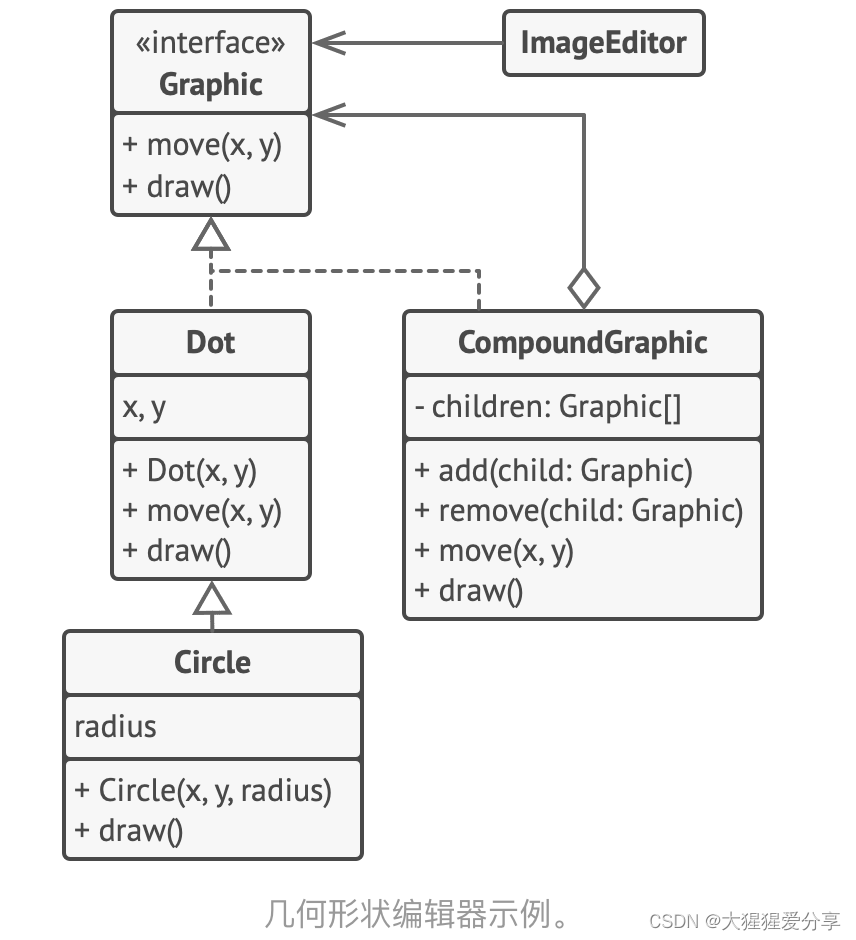
设计模式——组合模式(结构型)
引言 组合模式是一种结构型设计模式, 你可以使用它将对象组合成树状结构, 并且能像使用独立对象一样使用它们。 问题 如果应用的核心模型能用树状结构表示, 在应用中使用组合模式才有价值。 例如, 你有两类对象: …...

鸿蒙小车之多任务调度实验
说到鸿蒙我们都会想到华为mate60:遥遥领先!我们一直领先! 我们这个小车也是采用的是鸿蒙操作系统,学习鸿蒙小车,让你遥遥领先于你的同学。 文章目录 前言一、什么是任务?为什么要有任务二、任务的状态三、任…...
【报错栏】(vue)Module not found: Error: Can‘t resolve ‘element-ui‘ in xxx
Module not found: Error: Cant resolve element-ui in xxx 报错原因是: 未安装 element-ui 依赖 解决: npm install element-ui 运行...
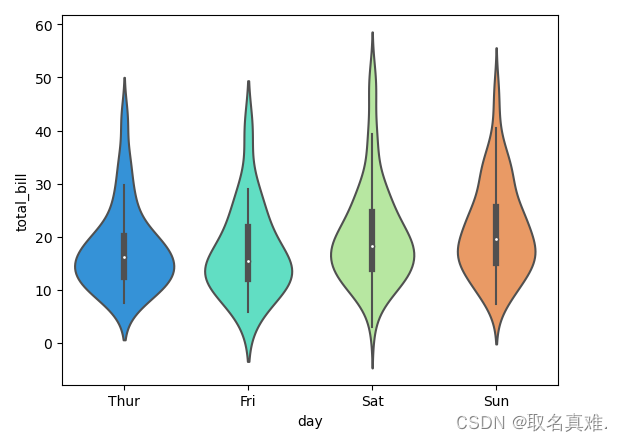
seaborn库图形进行数据分析(基于tips数据集)
Seaborn 是一个基于 matplotlib 的数据可视化库,可以用来绘制各种统计图表,包括散点图、条形图、折线图、箱线图等。Seaborn 提供了一些用于美化图表的默认样式和颜色主题,使得生成的图表更具有吸引力。下面是一些 Seaborn 库的常用功能和用法…...
AC843. n皇后问题--60
我们只需要把蓝色的往上移动就行了 if(!col[i][j]&&!dg[ui]&&!udg[])//1y(i)向下,x(u)向右为正。yxb的by-x一定>0,y-xb的bxy可能>0,这个不考虑,只看-bxy....

Js WebSocket类,收发Json,带心跳,断线重连
如题 心跳:4秒发一次 断线:2秒后自动重连 收发:发送和返回json,处理粘包断包等情况,json字符串最大长度9999 缓存:未连接时,自动缓存100个包,当连接时会自动发出 JS代码 var MyWeb…...

VBA技术资料MF96:单字段多条件高级筛选
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...
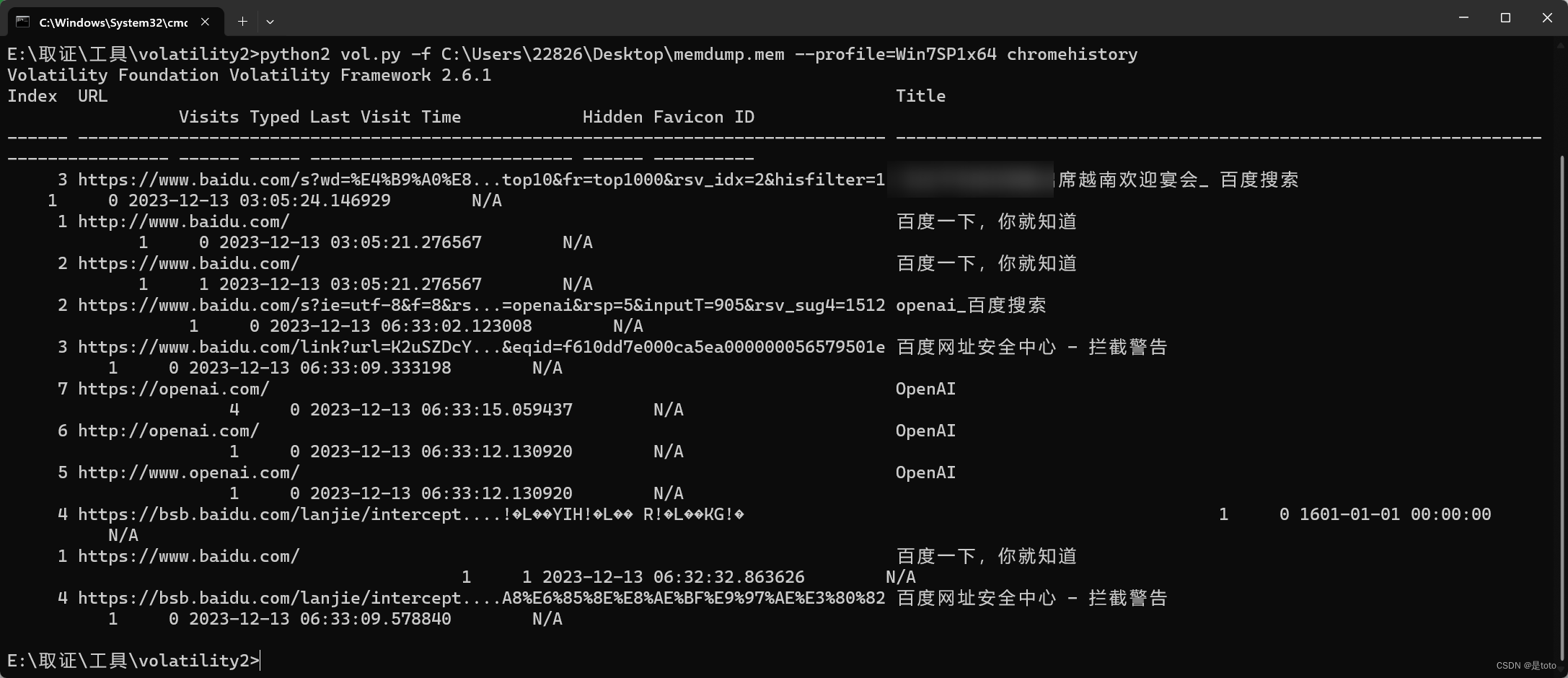
电子取证中Chrome各版本解密Cookies、LoginData账号密码、历史记录
文章目录 1.前置知识点2.对于80.X以前版本的解密拿masterkey的几种方法方法一 直接在目标机器运行Mimikatz提取方法二 转储lsass.exe 进程从内存提取masterkey方法三 导出SAM注册表 提取user hash 解密masterkey文件(有点麻烦不太推荐)方法四 已知用户密…...

Axure元件基本介绍进阶
Axure元件基本介绍进阶 1.Axure元件基本介绍1.在 Axure 中,元件是构建原型的基本构成单元,能够帮助设计师快速创建、重复使用和管理设计元素。以下是 Axure 中元件的基本介绍:1.基本元件: 2.基本元件的使用一.【举例说明】积木&am…...

安卓11添加切换以太网动态静态方法
客户要在app中自由切换动态,静态方法,直接把系统jar-api给他搞了半天搞不定,只有在系统里给他实现一个接口,方法如下: Index: packages/apps/Settings/AndroidManifest.xml--- packages/apps/Settings/AndroidManifes…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
