疯狂SQL转换系列- SQL for Tencent Cloud VectorDB
为了尽量保证使用者通过统一的SQL标准访问各类型数据库,我们这里开启了“疯狂SQL转换系列”。转换的语法效果不一定是最好的,更多是为用户提供一个统一的数据库交互体验。转换数据库目标的确认更多是内生的。基于我们对业务发展的需要。该向量库SQL转换的源码参见https://github.com/colorknight/moql-transx。
对腾讯云向量数据库的支持,主要是为了给LLM的RAG(检索增强生成)提供更多向量库选择。使用者可通过该接口输入SQL语句,获得结构化的数据结果,如下列代码示例:
// 构建TcVector客户端
ConnectParam connectParam = ConnectParam.newBuilder().withUrl("向量数据库url").withUsername("root").withKey("访问key").withTimeout(30).build();
vectorDBClient = new VectorDBClient(connectParam,
// 使用TcVector客户端创建TcVector查询器
TcVectorQuerier querier = new TcVectorQuerier(vectorDBClient);
/* 查询语句含义:从book集合中筛选数据,并返回全部列。筛选条件为,向量字段值为'[[0.3123, 0.43, 0.213], [0.5123, 0.63, 0.413]]'。取前2条命中记录。*/
String sql = "select * from datayoo.book where withVectors('[[0.3123, 0.43, 0.213], [0.5123, 0.63, 0.413]]') limit 2";
// 使用查询器执行sql语句,并返回查询结果
RecordSet recordSet = querier.query(sql);TcVector提供的检索接口与SQL语法有一定差异,其SearchParam提供的部分参数可以直接映射为SQL语法的等同语义子句。如:expr参数,其语义与SQL中Where子句语义基本兼容;其OutFields参数为输出结果集的列结构,与SQL语句的Select子句语义相同。但其也有其特殊的查询参数接口,如:针对向量字段匹配的参数接口withVectors等。由于这些概念在SQL中没有对应语义的子句,为不增加语法概念,MOQL Transx将这类接口都以Where子句中的函数形式进行表达。这种表达方式可能不是最佳表达方式,如果有人有更好的建议,可以到项目中给我们留言。
下表将给出TcVector查询接口的参数与SQL语法的对照关系:
| TcVector查询参数接口 | SQL语法 |
|---|---|
| collection(table) | from table |
| withOutputFields(outFields) | select outFields |
| withDocumentIds | where id = ? |
| withFilter | where expr |
| withParams | withParams |
| withVectors | withVectors |
| withLimit() | limit offset, k |
模块的maven坐标
<dependency><groupId>org.datayoo.moql</groupId><artifactId>moql-querier-tcvector</artifactId><version>1.0.0</version>
</dependency>相关文章:

疯狂SQL转换系列- SQL for Tencent Cloud VectorDB
为了尽量保证使用者通过统一的SQL标准访问各类型数据库,我们这里开启了“疯狂SQL转换系列”。转换的语法效果不一定是最好的,更多是为用户提供一个统一的数据库交互体验。转换数据库目标的确认更多是内生的。基于我们对业务发展的需要。该向量库SQL转换的…...

Excel中的INDIRECT函数用法
当在 Excel 中使用 INDIRECT 函数时,它可以帮助我们通过引用字符串中的单元格地址来获取对应单元格的值。这个函数非常有用,特别是在需要动态地引用其他单元格的情况下。下面是 INDIRECT 函数的一些用法和示例: 基本用法: INDIREC…...
Spring-temp
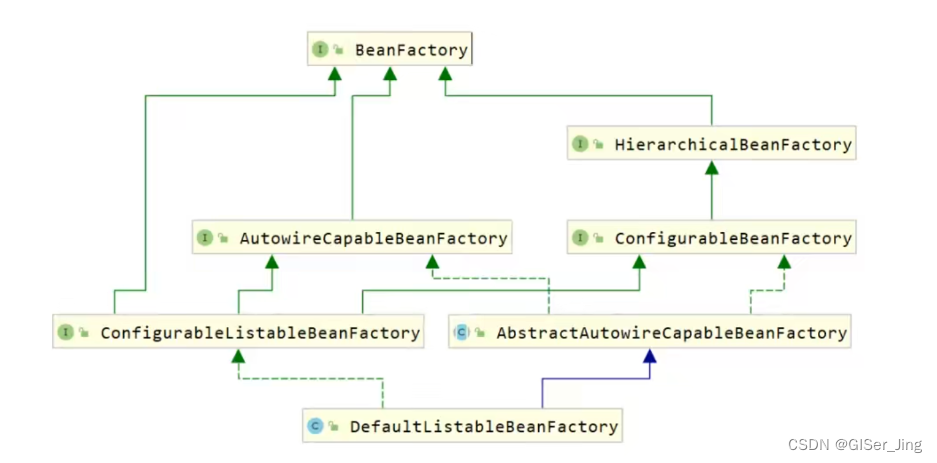
IOC/DI实现步骤 1.配置元数据 2.实例化IOC 3.获取Bean 基于XML配置方式 管理组件 1.基于构造函数:有参、无参 2.基于静态工厂方法:有参、无参 依赖注入 1.构造函数 2.setter方法 Bean组件高级特性 1.作用域 2.生命周期 FactoryBean 基于注解 IOC Bean作…...
【C++干货铺】会搜索的二叉树(BSTree)
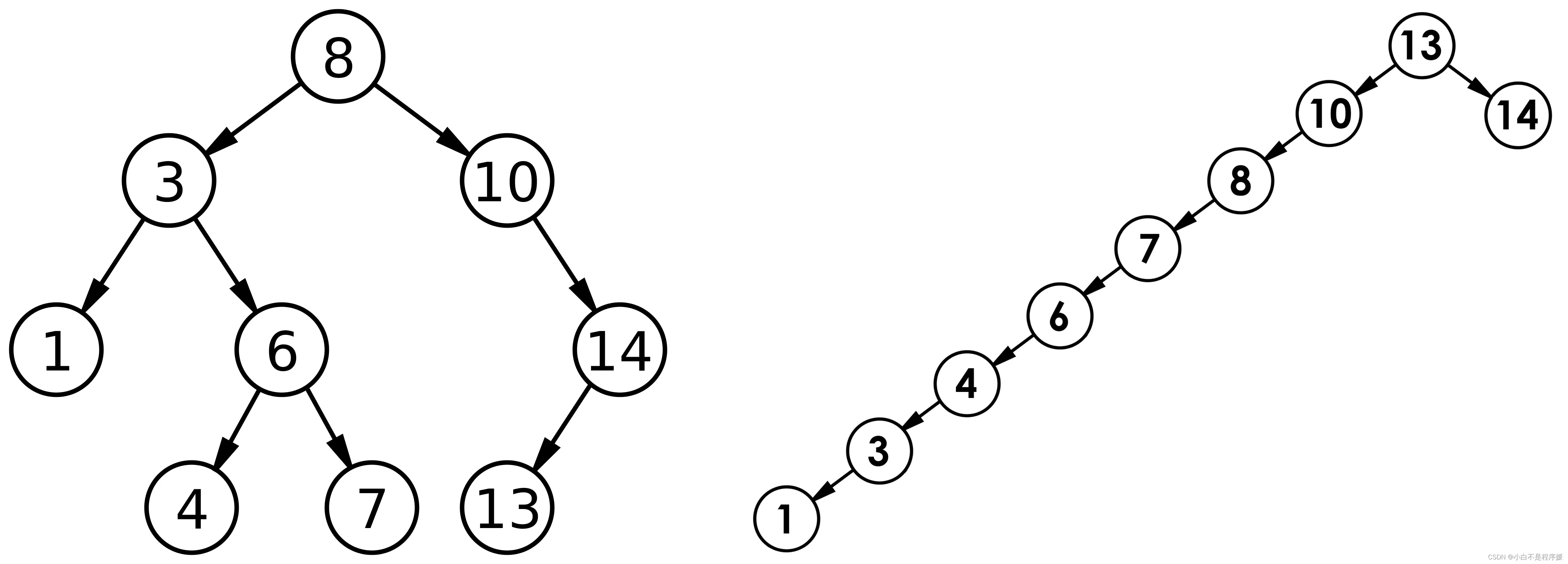
个人主页点击直达:小白不是程序媛 C系列专栏:C干货铺 代码仓库:Gitee 目录 前言: 二叉搜索树 二叉搜索树概念 二叉搜索树操作 二叉搜索树的查找 二叉搜索树的插入 二叉搜索树元素的删除 二叉搜索树的实现 BSTree结点 …...

【Spring AOP】 动态代理
一.AOP常见的实现方式 1.Spring AOP 2.aspectJ 注意:spring使用的是aspectJ的注解,但实现是spring自身实现的. 二.AOP原理 Spirng AOP原理 , 基于动态代理实现的. 三.代理模式 作用就是提供一个代理类,让我们在调用目标方法的时候,不再是直接对目标方法进行调用,而是通过代理类…...
NAT——网络地址转换
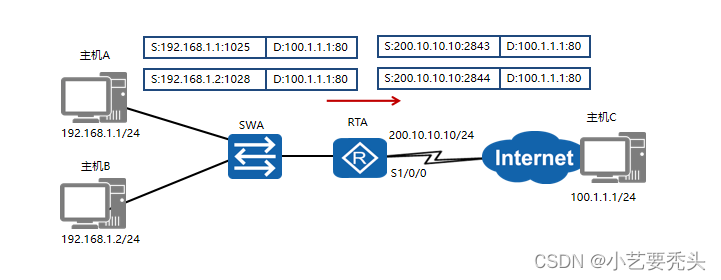
目录 一、概念 二、NAT的分类 1.静态NAT 1.1 静态NAT的配置 1.2 利用eNSP小实验加强对静态NAT的理解 2、动态NAT 三、NAPT——端口映射 四、Easy IP 使用一个公网地址可以让所有人都上公网 一、概念 随着Internet的发展和网络应用的增多,IPv4地址枯竭已经成为…...

Lambda 表达式的常见用法
文章目录 Lambda 表达式的常见用法使用Lambda表达式集合遍历使用Lambda表达式排序使用Lambda表达式过滤使用Lambda表达式映射使用Lambda表达式归约使用Lambda表达式分组使用Lambda表达式函数式接口的实现使用Lambda表达式线程的创建使用Lambda表达式进行Optional 操作使用Lambd…...

成本管理常用的ChatGPT通用提示词模板
成本分析:如何进行成本分析? 成本核算:如何进行成本核算? 成本控制:如何控制成本? 成本效益分析:如何进行成本效益分析? 成本预测:如何预测成本? 成本决…...

如何在PHP中处理日期和时间?
在 PHP 中,你可以使用内置的 DateTime 类和相关函数来处理日期和时间。以下是一些常见的日期和时间操作的示例: 使用 DateTime 类: 获取当前日期和时间: $currentDateTime new DateTime(); echo $currentDateTime->format(Y-…...

NO-IOT翻频,什么是翻频,电信为什么翻频
1.1 翻频迁移最终的目的就是减少网络的相互干扰,提供使用质量. 1.2 随着与日俱增的网络规模的扩大,网内干扰已成了影响网络的质量标准之一,为了保障电信上网体验,满足用户日益增长的网速需求,更好的服务客户,电信针对…...

云原生之深入解析OOM和CPU节流
一、前言 使用 Kubernetes 时,内存不足 (OOM) 错误和 CPU 节流是云应用程序中资源处理的主要难题,这是为什么呢?云应用程序中的 CPU 和内存要求变得越来越重要,因为它们与云成本直接相关。通过 limits 和 requests ,可…...
)
数据结构与算法之递归: LeetCode 93. 复原 IP 地址 (Typescript版)
复原 IP 地址 https://leetcode.cn/problems/restore-ip-addresses/ 描述 有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 ‘.’ 分隔。 例如:“0.1.2.201” 和 “192.…...

json模块与jsonpath详解
数据提取之JSON与JsonPATH JSON(JavaScript Object Notation) 是一种轻量级的数据交换格式,它使得人们很容易的进行阅读和编写。同时也方便了机器进行解析和生成。适用于进行数据交互的场景,比如网站前台与后台之间的数据交互。 JSON和XML的比较可谓不…...

ubuntu20.04在noetic下编译orbslam2
ubuntu20.04在noetic下编译orbslam2 参考链接1:https://blog.csdn.net/qq_58869016/article/details/128660588 参考链接2:https://blog.csdn.net/dong123456789e/article/details/129693837 在noetic下的安装环境 1.库安装 sudo apt-get update sudo …...
64. 最小路径和
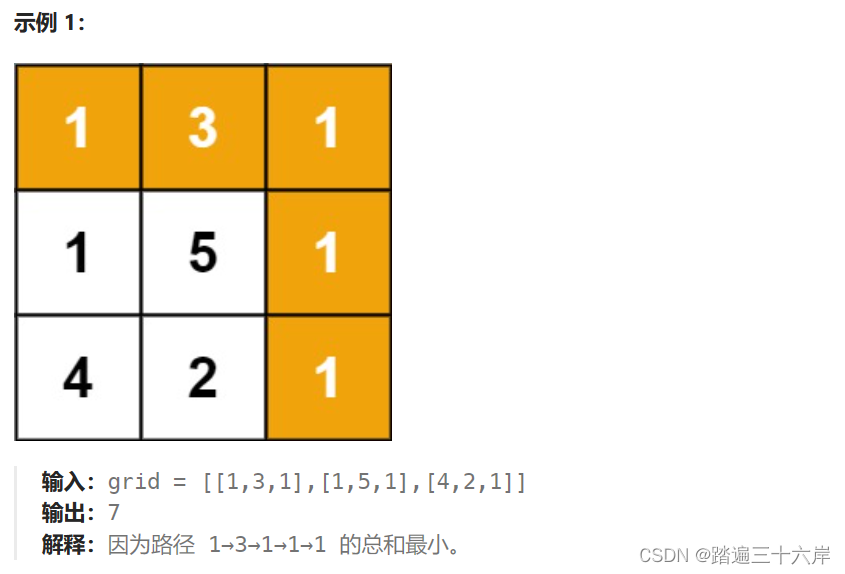
最小路径和 描述 : 给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。 说明:每次只能向下或者向右移动一步。 题目 : LeetCode 64.最小路径和 64. 最小路径和 解析 : class So…...
)
惰性加载函数(js的问题)
在web开发中,因为浏览器之间的实现差异,一些嗅探工作总是不可避免。 var addEvent function( elem, type, handler ){if ( window.addEventListener ){return elem.addEventListener( type, handler, false );}if ( window.attachEvent ){return elem.…...
jmeter,读取CSV文件数据的循环控制
1、构造csv数据 保存文件时需要注意文件的编码格式 id,name,limit,status,address,start_time 100,小米100,1000,1,某某会展中心101,2023/8/20 14:20 101,小米101,1001,1,某某会展中心102,2023/8/21 14:20 2、在线程组下添加【CSV数据文件设置】元件 3、CSV文件数据的循环控…...

移植LVGL到像素屏,从此玩转像素屏0门槛
硬件方面 先上渲染图 实物图 配置 主控:esp32 micro32 plus主频:240MhzFlash:8MPSRAM:2M 软件方面 众所周知,LVGL是一个十分优秀的图形框架,小到几百kb的单片机,大到Linux都可以运行。既然它…...
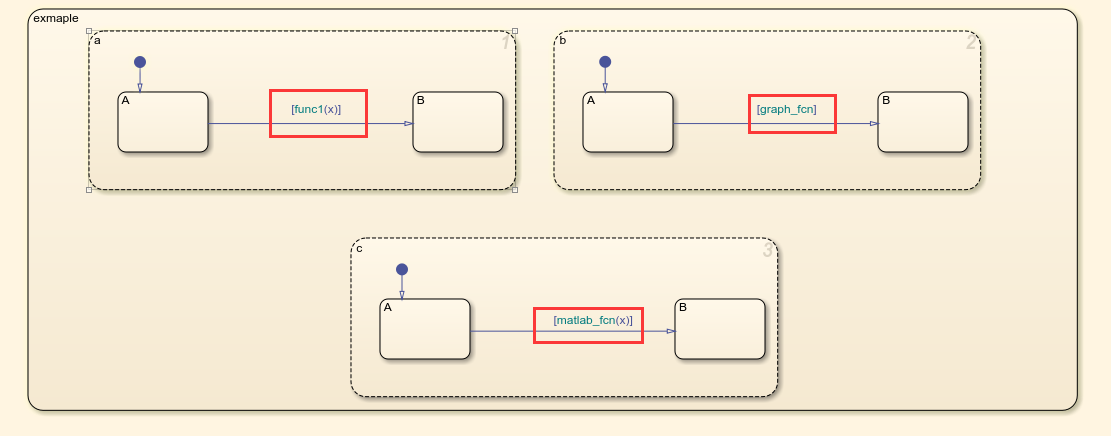
stateflow 之图函数、simulink函数和matlab函数使用及案例分析
目录 前言 1. 图函数graph function 2.simulink function 3.matlab function 4.调用stateflow中的几种函数方式 前言 对于stateflow实际上可以做simulink和matlab的所有任务,可以有matlab的m语言,也可以有simulink的模块,关于几种函数在…...

C# 加载本地文件设置应用程序图标
static class Program{[STAThread]static void Main(){Application.EnableVisualStyles();Application.SetCompatibleTextRenderingDefault(false);Form mainForm new Form1();mainForm.Show();//IntPtr hProcess Process.GetCurrentProcess().MainWindowHandle;// 设置应用程…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

Qt Quick Controls模块功能及架构
Qt Quick Controls是Qt Quick的一个附加模块,提供了一套用于构建完整用户界面的UI控件。在Qt 6.0中,这个模块经历了重大重构和改进。 一、主要功能和特点 1. 架构重构 完全重写了底层架构,与Qt Quick更紧密集成 移除了对Qt Widgets的依赖&…...

深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀”
深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀” 在JavaScript中,我们经常需要处理文本、数组、对象等数据类型。但当我们需要处理文件上传、图像处理、网络通信等场景时,单纯依赖字符串或数组就显得力不从心了。这时ÿ…...

自定义线程池1.2
自定义线程池 1.2 1. 简介 上次我们实现了 1.1 版本,将线程池中的线程数量交给使用者决定,并且将线程的创建延迟到任务提交的时候,在本文中我们将对这个版本进行如下的优化: 在新建线程时交给线程一个任务。让线程在某种情况下…...
