leetcode: Two Sum
leetcode: Two Sum
- 1. 题目
- 1.1 题目描述
- 2. 解答
- 2.1 baseline
- 2.2 基于baseline的思考
- 2.3 优化思路的实施
- 2.3.1 C++中的hashmap
- 2.3.2 实施
- 2.3.3 再思考
- 2.3.4 最终实施
- 3. 总结
1. 题目
1.1 题目描述
Given an array of integers nums and an integer target, return indices of the two
numbers such that they add up to target. You may assume that each input would have
exactly one solution, and you may not use the same element twice.
You can return the answer in any order.
Example 1:
Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].
Example 2:
Input: nums = [3,2,4], target = 6
Output: [1,2]
Example 3:
Input: nums = [3,3], target = 6
Output: [0,1]
Constraints:
- 2 <= nums.length <= 104
- -109 <= nums[i] <= 109
- -109 <= target <= 109
- Only one valid answer exists.
2. 解答
2.1 baseline
一个比较直观的想法是,罗列出所有的可能方案,然后找到和等于target的方案,返回即可。这里面蕴含的数学概念是:组合,从n个元素中取出2个元素; 用数学公式表示为cn2c_{n}^{2}cn2。
在用代码表示cn2c_{n}^2cn2之前,可以先绘制一下示意图:
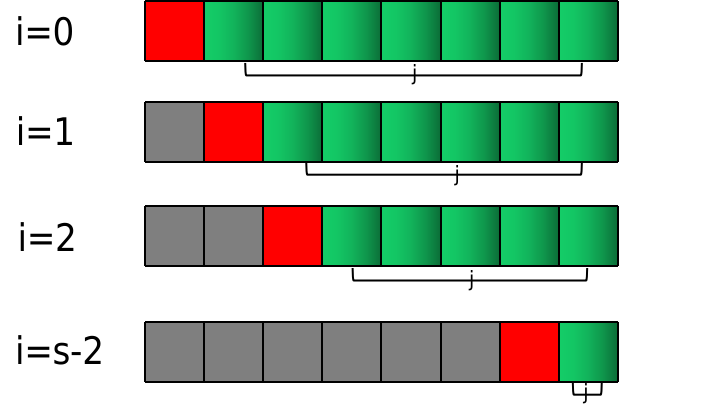
根据该示意图不难写出对应的代码。
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {for(int i = 0; i < nums.size() - 1; ++i){for(int j = i + 1; j < nums.size(); ++j){if(target == nums[i] + nums[j]){return {i, j};}}}return {-1, -1};}
};
2.2 基于baseline的思考
baseline是一种“Brute Force”的思想,它的时间复杂度是o(n2)o(n^2)o(n2),这个时间复杂度极大概率不是最优的。
多层循环的常用优化点在于将循环解耦。例如将o(n2)o(n^2)o(n2)----->o(n)+o(n)o(n) + o(n)o(n)+o(n)。外层循环表示的含义是数组中的每一个元素都有机会作为候选答案。因此这层循环很难去除。
来看内层循环:内层循环在做的事情是对于当前nums[i]nums[i]nums[i], 通过遍历数组的方式,确认是否在其他元素中存在与之相加等于sum的元素;如果有找到答案。加粗的几个词语,是优化的关键:
“Brute Force”之所以效率低,是因为它在内循环中,试图以数组这一种数据结构,来解决查找问题。而数组的查找智能以遍历的方式进行,其查找的时间复杂度为n。
而哈希表(hashmap)这种数据结构,可以做到查找问题以o(1)o(1)o(1)的时间复杂度进行。因此在进行真正的解决方案之前,先要根据数组构建对应的hashmap,以这种辅助数据的方式,将两层for循环进行解耦,从而时间复杂度降低为o(n)+o(n)o(n) + o(n)o(n)+o(n)。
2.3 优化思路的实施
2.3.1 C++中的hashmap
hashmap(哈希表)是一个概念,不同编程语言对其有自己的实现。c++将其实现为std::unordered_map形式,(这边需要强调,不是std::map,std::map是对read-black tree的实现,其插入元素和访问元素的时间复杂度是log(n)log(n)log(n))。
具体相关的代码有:
#include <unordered_map> // 头文件
std::unordered_map<int, int> um; // 定义一个unordered_map 对象
um.contains(k); //判断k键值是否在um中,该时间复杂度是o(1) c++20才支持
um.find(k) != um.end(); //判断k键值是否在um中,该时间复杂度是o(1) c++11才支持
int index = um[k]; //获得k健值对应的value,该时间复杂度为o(1)
2.3.2 实施
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {std::unordered_map<int, int> um;for(int i = 0; i < nums.size(); ++i){um[nums[i]] = i;}for(int i = 0; i < nums.size(); ++i){int another = target - nums[i];if(um.find(another) != um.end() && um[another] != i)return {i, um[another]};}return {-1, -1};}
};
这里要注意一下
um[another] != i
主要是对应题干中的you may not use the same element twice.
2.3.3 再思考
但该方案提交leetcode之后,耗时仍旧位于第二峰值区域。说明有继续优化的空间。目前的方案时间复杂度为o(N)+o(n)o(N) + o(n)o(N)+o(n), 大写字母N表示是构建哈希表的部分,必须要遍历掉所有的元素;小写o(n)则是大概率仅仅会遍历部分元素,在中途就会找到答案中途退出。因此o(N)o(N)o(N)是当前的瓶颈。这里面细分,o(N)o(N)o(N)是存在冗余信息的:
对于当前待查找对象nums[i], 我们只需知道在该元素之前是否有与之能够成功匹配的元素即可。因为若出现与nums[i]匹配的元素nums[ii]在i之后,则在处理元素nums[ii]的时候,nums[i]是作为ii之前,已经存在于hash表中的。这个时候nums[i]仍旧能够被翻出来。
这样做的好处在于将o(N)+o(n)o(N) + o(n)o(N)+o(n)转变为o(n)+o(n)o(n) + o(n)o(n)+o(n)。
2.3.4 最终实施
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {std::unordered_map<int, int> um;for(int i = 0; i < nums.size(); ++i){int another = target - nums[i];if(um.find(another) != um.end())return {i, um[another]};um[nums[i]] = i; }return {-1, -1};}
};
此时的解决方案,就可以位于第一峰值处。

3. 总结
虽然"Brute Force"解法一般不是最优的,但快速的写出该解法作为baseline,是做进一步分析的前提。
分析耗时的瓶颈所在:两层for循环导致的o(n2)o(n^2)o(n2)时间复杂度。往往可以借助于“辅助数据结构”,解耦到"o(N) + o(N)"的方案。而hashmap作为可以获得常量级插入和访问的数据结构,是非常优质的,需要熟悉其用法。
若想要进一步优化,“o(N) + o(n)” --> "o(n) + o(n)"是一种手段。因为此时的瓶颈在于o(N)。
最后在大的框架代码写完之后,要思考题干中的特殊限制代表的含义,例如you may not use the same element twice. 思考自己的代码是否已经体现了其含义。
相关文章:

leetcode: Two Sum
leetcode: Two Sum1. 题目1.1 题目描述2. 解答2.1 baseline2.2 基于baseline的思考2.3 优化思路的实施2.3.1 C中的hashmap2.3.2 实施2.3.3 再思考2.3.4 最终实施3. 总结1. 题目 1.1 题目描述 Given an array of integers nums and an integer target, return indices of the …...

共享模型之无锁(三)
1.原子累加器 示例代码: public class TestAtomicAdder {public static void main(String[] args) {for (int i 0; i < 5; i) {demo(() -> new AtomicLong(0),(adder) -> adder.getAndIncrement());}for (int i 0; i < 5; i) {demo(() -> new LongAdder(),(…...
微信小程序 Springboot校运会高校运动会管理系统
3.1小程序端 小程序登录页面,用户也可以在此页面进行注册并且登录等。 登录成功后可以在我的个人中心查看自己的个人信息或者修改信息等 在广播信息中我们可以查看校运会发布的一些信息情况。 在首页我们可以看到校运会具体有什么项目运动。 在查看具体有什么活动我…...

走进独自开,带你轻松干副业
今天给大家分享一个开发者的福利平台——独自开(点击直接注册),让你在家就能解决收入问题。 文章目录一、平台介绍二、系统案例三、获取收益四、使用平台1、用户注册2、用户认证3、任务报价五、文末总结一、平台介绍 简单说明 独自开信息科技…...
SpringBoot+Vue实现师生健康信息管理系统
文末获取源码 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏…...

数据库第四章节第三次作业内容
1、显示所有职工的基本信息。 2、查询所有职工所属部门的部门号,不显示重复的部门号。 3、求出所有职工的人数。 4、列出最高工和最低工资。 5、列出职工的平均工资和总工资。 6、创建一个只有职工号、姓名和参加工作的新表,名为工作日期表…...

一篇五分生信临床模型预测文章代码复现——FIgure 9.列线图构建,ROC分析,DCA分析 (四)
之前讲过临床模型预测的专栏,但那只是基础版本,下面我们以自噬相关基因为例子,模仿一篇五分文章,将图和代码复现出来,学会本专栏课程,可以具备发一篇五分左右文章的水平: 本专栏目录如下: Figure 1:差异表达基因及预后基因筛选(图片仅供参考) Figure 2. 生存分析,…...

神经网络实战--使用迁移学习完成猫狗分类
前言: Hello大家好,我是Dream。 今天来学习一下如何使用基于tensorflow和keras的迁移学习完成猫狗分类,欢迎大家一起前来探讨学习~ 本文目录:一、加载数据集1.调用库函数2.加载数据集3.数据集管理二、猫狗数据集介绍1.猫狗数据集介…...
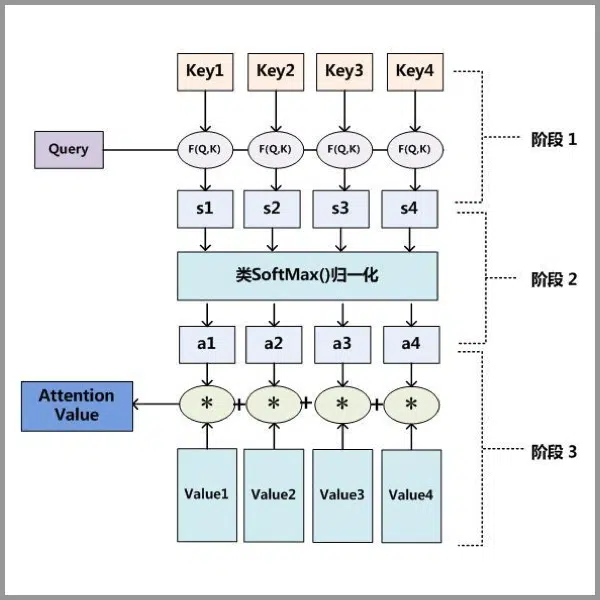
Attention机制 学习笔记
学习自https://easyai.tech/ai-definition/attention/ Attention本质 Attention(注意力)机制如果浅层的理解,跟他的名字非常匹配。他的核心逻辑就是“从关注全部到关注重点”。 比如我们人在看图片时,对图片的不同地方的注意力…...

数据类型与运算符
1.字符型作用: 字符型变量用于显示单个字符语法: char cc a ;注意1: 在显示字符型变量时,用单引号将字符括起来,不要用双引号注意2: 单引号内只能有一个字符,不可以是字符串C和C中字符型变量只占用1个字节。字符型变是并不是把字符本身放到内存中存储&am…...

算法刷题-二叉树的锯齿形层序遍历、用栈实现队列 栈设计、买卖股票的最佳时机 IV
文章目录二叉树的锯齿形层序遍历(树、广度优先搜索)用栈实现队列(栈、设计)买卖股票的最佳时机 IV(数组、动态规划)二叉树的锯齿形层序遍历(树、广度优先搜索) 给定一个二叉树&…...
| 代码编写思路+核心知识点)
华为OD机试 - 最小传递延迟(Python)| 代码编写思路+核心知识点
最小传递延迟 题目 通讯网络中有 N 个网络节点 用 1 ~ N 进行标识 网络通过一个有向无环图进行表示 其中图的边的值,表示节点之间的消息传递延迟 现给定相连节点之间的延时列表 times[i]={u,v,w} 其中 u 表示源节点,v 表示目的节点,w 表示 u 和 v 之间的消息传递延时 请计…...
集中供热调度系统天然气仪表内网仪表图像识别案例
一、项目需求 出于能耗采集与冬季集中供暖工作的节能和能耗分析需要,要采集现场的6块天然气表计,并存储进入客户的mySQL数据库中,现场采集的表计不允许接线,且网络环境为内网环境,需要采集表计数据并存入数据库&#…...

笔试题-2023-复旦微-数字IC设计【纯净题目版】
回到首页:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录 推荐内容:数字IC设计学习比较实用的资料推荐 题目背景 笔试时间:2022.07.26应聘岗位:数字前端工程师笔试时长:120min笔试平台:赛码题目类型:基础题(10道)、选做题(10道)、验证题(5道)主观评价 难…...
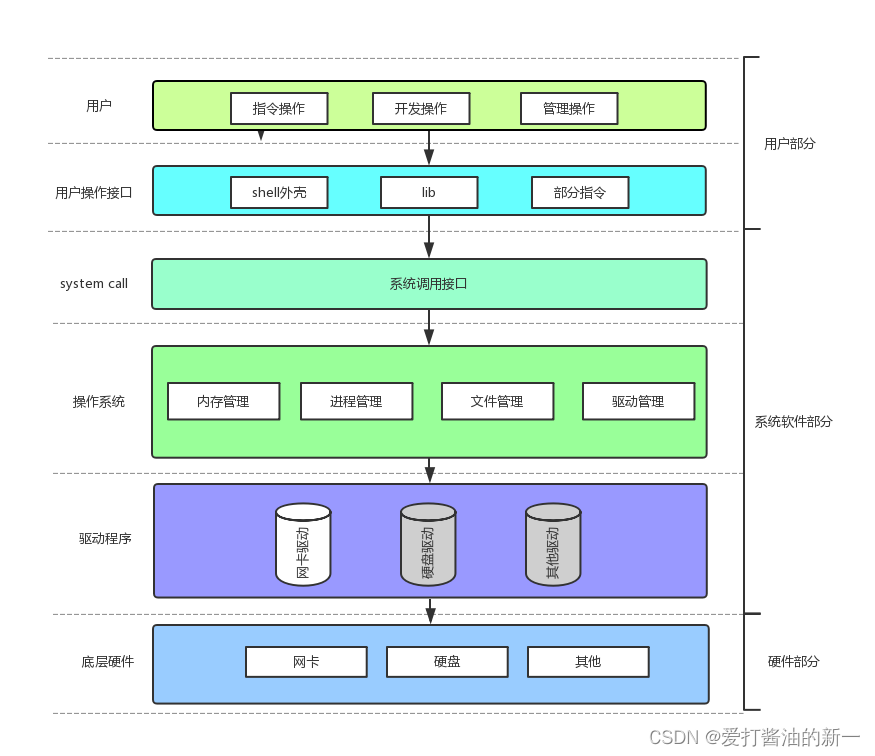
【Linux】冯诺依曼体系结构和操作系统概念
文章目录🎪 冯诺依曼体系结构🚀1.体系概述🚀2.CPU和内存的数据交换🚀3.体系结构中数据的流动🎪 操作系统概念理解🚀1.简述🚀2.设计目的🚀3.定位🚀4.理解🚀5.管…...
HTML5之HTML基础学习笔记
列表标签 列表的应用场景 场景:在网页中按照行展示关联性的内容,如:新闻列表、排行榜、账单等特点:按照行的方式,整齐显示内容种类:无序列表、有序列表、自定义列表 这是老师PPT上的内容, 列表…...

FreeRTOS信号量 | FreeRTOS十
目录 说明: 一、信号量 1.1、信号量简介 1.2、信号量特点 二、二值信号量 2.1、二值信号量简介 2.2、获取与释放二值信号量函数 2.3、二值信号量使用过程与相关API函数 2.4、创建二值信号量函数了解 2.5、释放二值信号量了解 2.6、获取二值信号量了解 三…...

【SpringBoot】SpringBoot常用注解
一、前言首先这里说的SpringBoot常用注解是指在我们开发项目过程中,我们经常使用的注解,包含Spring、SpringBoot、SpringCloud、SpringMVC等这些框架中的注解,而不仅仅是SpringBoot中的注解。这里只是作一个注解列举,每个注解具体…...
数据一致性
目录一、AOP 动态代理切入方法(1) Aspect Oriented Programming(2) 切入点表达式二、SpringBoot 项目扫描类(1) ResourceLoader 扫描类(2) Map 的 computeIfAbsent 方法(3) 反射几个常用 api① 创建一个测试注解② 创建测试 PO 类③ 反射 api 获取指定类的指定注解信息(4) 返回…...
Docker不做虚拟化内核,对.NET有什么影响?
引子前两天刷抖音,看见了这样一个问题。问题:容器化不做虚拟内核,会有什么弊端?Java很多方法会跟CPU的核数有关,这个时候调用系统函数,读到的是宿主机信息,而不是我们限制资源的大小。思考&…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
