【机器学习】从底层手写实现线性回归
【机器学习】Building-Linear-Regression-from-Scratch
- 线性回归 Linear Regression
- 0. 数据的导入与相关预处理
- 0.工具函数
- 1. 批量梯度下降法 Batch Gradient Descent
- 2. 小批量梯度下降法 Mini Batch Gradient Descent(在批量方面进行了改进)
- 3. 自适应梯度下降法 Adagrad(在学习率方面进行了改进)
- 4. 多变量线性回归 Multivariate Linear Regression(在特征方面进行了改进,拓展到多个特征)
- 5. L1正则化 L1 Regularization(在正则化方面进行了改进)
This project is not about using ready-made libraries; it’s an exploration into the core principles that power linear regression. We start from basic mathematics and progressively build up to a fully functioning linear regression model. This hands-on approach is designed for learners and enthusiasts who want to deeply understand the intricacies of one of the most fundamental algorithms in machine learning. Dive in to experience linear regression like never before!
这个项目不是关于使用现成的库,而是对驱动线性回归的核心原则的一次探索。我们从基础数学开始,逐步构建出一个功能完善的线性回归模型。这种实践方法专为那些希望深入理解机器学习中最基本算法之一的复杂性的学习者和爱好者设计。深入体验前所未有的线性回归!
If you find the code helpful, please give me a Star.
如果觉得代码对你有帮助,请给我一个Star.
前往Github下载notebook
https://github.com/Zhu-Shatong/Building-Linear-Regression-from-Scratch
线性回归 Linear Regression
CopyRight: Zhu Shatong , Tongji University
本notebook所有算法均为手写,不使用任何库函数。
(算法设计部分)目录:
- 准备工作:数据的导入与相关预处理,相关工具函数的定义
- (单变量线性回归的)批量梯度下降法 Batch Gradient Descent
- 小批量梯度下降法 Mini Batch Gradient Descent(在批量方面进行了改进)
- 自适应梯度下降法 Adagrad(在学习率方面进行了改进)
- 多变量线性回归 Multivariate Linear Regression(在特征方面进行了改进,拓展到多个特征)
- L1正则化 L1 Regularization(也就是Lasso Regression,应对多变量的过拟合)
0. 数据的导入与相关预处理
在这一section, 我们将会负责导入数据,并对数据进行一些预处理,以便于后续的操作。
data:
我们首先导入的文件为 data.xlsx ,将它存储在data变量中。这个文件中包含了两列数据,分别为 x 和 y 。
我们将会使用这些数据来进行线性回归的训练与可视化。
请注意,在后续本notebook中使用其他数据的时候,请勿再次命名为data。
数据来源:
Data on length-weight and length-length relationships, mean condition factor, and gonadosomatic index of Rutilus rutilus and Perca fluviatilis from the Ob River basin, Western Siberia - ScienceDirect
# 这一code block用来import需要的库import pandas as pd # 用来读取excel等文件
import random # 用来进行随机打乱数据
import numpy as np # 用来进行矩阵运算,应对多变量线性回归
# 这一code block用来读取数据data = pd.read_excel("data.xlsx") # 读取excel文件(单变量线性回归——测试文件)
# 这一code block用来对读取的数据进行一些处理# 从数据框架中提取x和y值
x_values = data['x'].values
y_values = data['y'].values
0.工具函数
在这一section, 我们将会定义一些工具函数,以便于后续的操作。
目录:
- 可视化工具函数
- 线性回归模型计算
- 损失函数计算
# 可视化工具函数
# 对于数据点与拟合直线的可视化
def plot_data_and_line(x_values, y_values, theta_0_final, theta_1_final, cost_history, title):"""Plot data points and the fitted line.:param x_values: 这是一个list,包含了所有的x值:param y_values: 这是一个list,包含了所有的y值:param theta_0_final: 这是一个float,表示最终的theta_0:param theta_1_final: 这是一个float,表示最终的theta_1:param cost_history: 这是一个list,包含了每一次迭代后的损失函数值:param title: 这是一个string,表示图像的标题:return: 返回一个图像"""import matplotlib.pyplot as plt # 用来画图plt.figure(figsize=(12, 5))# Subplot 1: Linear Regression# 这个subplot用来画出数据点和拟合直线plt.subplot(1, 2, 1)plt.scatter(x_values, y_values, color='blue', label='Original Data') # 这里的scatter用来画出数据点plt.plot(x_values, [f_theta(x, theta_0_final, theta_1_final) for x in x_values], color='red',label='Linear Regression') # 这里的列表表达式用来画出拟合直线plt.title(title)plt.xlabel('x')plt.ylabel('y')plt.legend()plt.grid(True) # 显示网格# Subplot 2: Cost function history# 这个subplot用来画出损失函数的变化plt.subplot(1, 2, 2)plt.plot(cost_history, color='green') # 这里的plot用来画出损失函数的变化plt.title('Cost Function History')plt.xlabel('Iteration')plt.ylabel('Cost')plt.grid(True) # 显示网格plt.tight_layout() # 调整子图之间的间距plt.show()
hypothesis:
f θ ( x ) = θ 0 + θ 1 x f_\theta(x)=\theta_0+\theta_1x fθ(x)=θ0+θ1x
def f_theta(x, theta_0, theta_1):"""Linear regression model.:param x: 这是一个float,表示输入的x值:param theta_0: 这是一个float,表示theta_0:param theta_1: 这是一个float,表示theta_1:return: 这是一个float,表示预测值"""return theta_0 + theta_1 * x
cost fuction:
J ( θ 0 , θ 1 ) = 1 2 N ∑ i = 1 N ( f θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1)=\frac1{2N}\sum_{i=1}^N(f_\theta(x^{(i)})-y^{(i)})^2 J(θ0,θ1)=2N1i=1∑N(fθ(x(i))−y(i))2
def compute_cost(x_values, y_values, theta_0, theta_1):"""Compute the cost function.:param x_values: 这是一个list,包含了所有的x值:param y_values: 这是一个list,包含了所有的y值:param theta_0: 这是一个float,表示theta_0:param theta_1: 这是一个float,表示theta_1:return: 这是一个float,表示损失函数的值"""# 计算的公式为:J(theta_0, theta_1) = 1/2N * sum((f_theta(x_i) - y_i)^2)N = len(x_values)total_error = 0for i in range(len(x_values)):total_error += (f_theta(x_values[i], theta_0, theta_1) - y_values[i]) ** 2return total_error / (2 * N)
1. 批量梯度下降法 Batch Gradient Descent
repeat until convergence:
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) ( for j = 1 and j = 0 ) \theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1) \\ (\text{for }j=1\text{ and }j=0) θj:=θj−α∂θj∂J(θ0,θ1)(for j=1 and j=0)
Repeat until convergence:
θ 0 : = θ 0 − a 1 N ∑ i = 1 N ( f θ ( x ( i ) ) − y ( i ) ) θ 1 : = θ 1 − a 1 N ∑ i = 1 N ( f θ ( x ( i ) ) − y ( i ) ) x ( i ) \begin{aligned}\theta_0{:}&=\theta_0-a\frac1N\sum_{i=1}^N(f_\theta\big(x^{(i)}\big)-y^{(i)})\\\theta_1{:}&=\theta_1-a\frac1N\sum_{i=1}^N(f_\theta\big(x^{(i)}\big)-y^{(i)})x^{(i)}\end{aligned} θ0:θ1:=θ0−aN1i=1∑N(fθ(x(i))−y(i))=θ1−aN1i=1∑N(fθ(x(i))−y(i))x(i)
def gradient_descent(x_values, y_values, alpha=0.05, convergence_threshold=1e-8, max_iterations=10000):"""Perform gradient descent to learn theta_0 and theta_1.:param x_values: 这是一个list,包含了所有的x值:param y_values: 这是一个list,包含了所有的y值:param alpha: 这是一个float,表示学习率:param convergence_threshold: 这是一个float,表示收敛阈值:param max_iterations: 这是一个int,表示最大迭代次数:return: 这是一个tuple,包含了theta_0, theta_1, cost_history,分别表示最终的theta_0, theta_1和损失函数的变化"""# 计算公式为: theta_j = theta_j - alpha * 1/N * sum((f_theta(x_i) - y_i) * x_i)theta_0 = 0 # 初始化theta_0theta_1 = 0 # 初始化theta_1N = len(x_values) # 样本数量cost_history = [] # 用来保存损失函数的变化for _ in range(max_iterations): # 进行迭代sum_theta_0 = 0 # 用来计算theta_0的梯度sum_theta_1 = 0 # 用来计算theta_1的梯度for i in range(N):error = f_theta(x_values[i], theta_0, theta_1) - y_values[i] # 计算误差sum_theta_0 += errorsum_theta_1 += error * x_values[i]# 注意,所有的theta的更新都是在同一时刻进行的theta_0 -= alpha * (1 / N) * sum_theta_0theta_1 -= alpha * (1 / N) * sum_theta_1cost_history.append(compute_cost(x_values, y_values, theta_0, theta_1)) # 计算损失函数的值if len(cost_history) > 1 and abs(cost_history[-1] - cost_history[-2]) < convergence_threshold:# 如果损失函数的变化小于收敛阈值,则停止迭代breakreturn theta_0, theta_1, cost_history
# 这一code block用来调用上面的函数
theta_0_final, theta_1_final, cost_history = gradient_descent(x_values, y_values)# 打印最终的theta_0, theta_1, cost
theta_0_final, theta_1_final, cost_history[-1]
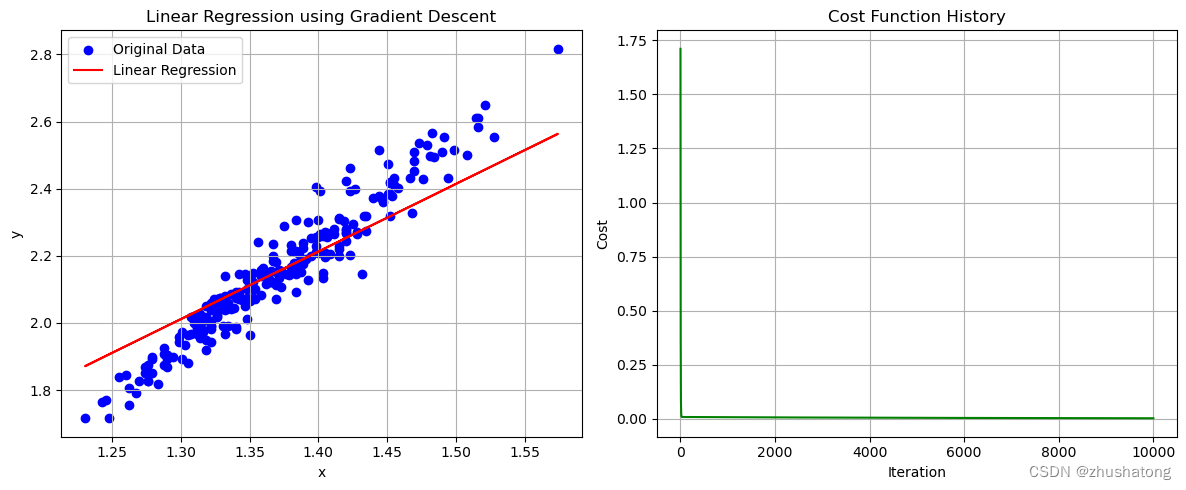
# 这一code block用来画出数据点和拟合直线
plot_data_and_line(x_values, y_values, theta_0_final, theta_1_final, cost_history,'Linear Regression using Gradient Descent')
2. 小批量梯度下降法 Mini Batch Gradient Descent(在批量方面进行了改进)
θ 0 : = θ 0 − a 1 N k ∑ i = 1 N k ( f θ ( x ( i ) ) − y ( i ) ) θ 1 : = θ 1 − a 1 N k ∑ i = 1 N k ( f θ ( x ( i ) ) − y ( i ) ) x ( i ) \begin{aligned}\theta_0&:=\theta_0-a\frac1{N_k}\sum_{i=1}^{N_k}(f_\theta\big(x^{(i)}\big)-y^{(i)})\\\theta_1&:=\theta_1-a\frac1{N_k}\sum_{i=1}^{N_k}(f_\theta\big(x^{(i)}\big)-y^{(i)})x^{(i)}\end{aligned} θ0θ1:=θ0−aNk1i=1∑Nk(fθ(x(i))−y(i)):=θ1−aNk1i=1∑Nk(fθ(x(i))−y(i))x(i)
def mini_batch_gradient_descent(x_values, y_values, batch_size=5, alpha=0.05, convergence_threshold=1e-8,max_iterations=10000):"""Perform mini batch gradient descent to learn theta_0 and theta_1.:param x_values: 这是一个list,包含了所有的x值:param y_values: 这是一个list,包含了所有的y值:param batch_size: 这是一个int,表示batch的大小:param alpha: 这是一个float,表示学习率:param convergence_threshold: 这是一个float,表示收敛阈值:param max_iterations: 这是一个int,表示最大迭代次数:return: 这是一个tuple,包含了theta_0, theta_1, cost_history,分别表示最终的theta_0, theta_1和损失函数的变化"""theta_0 = 0 # 初始化theta_0theta_1 = 0 # 初始化theta_1N = len(x_values)cost_history = []for _ in range(max_iterations):# 对数据进行随机打乱combined = list(zip(x_values, y_values)) # 将x_values和y_values打包成一个listrandom.shuffle(combined) # 对打包后的list进行随机打乱x_values[:], y_values[:] = zip(*combined) # 将打乱后的list解包赋值给x_values和y_values# Mini-batch updates# 这里的代码与batch gradient descent的代码类似,只是多了一个batch_size的参数# 对于每一个batch,都会计算一次梯度,并更新theta_0和theta_1for i in range(0, N, batch_size): # i从0开始,每次增加batch_sizex_batch = x_values[i:i + batch_size] # 从i开始,取batch_size个元素y_batch = y_values[i:i + batch_size] # 从i开始,取batch_size个元素sum_theta_0 = 0 # 用来计算theta_0的梯度sum_theta_1 = 0 # 用来计算theta_1的梯度for j in range(len(x_batch)): # 对于每一个batch中的元素error = f_theta(x_batch[j], theta_0, theta_1) - y_batch[j]sum_theta_0 += errorsum_theta_1 += error * x_batch[j]theta_0 -= alpha * (1 / batch_size) * sum_theta_0theta_1 -= alpha * (1 / batch_size) * sum_theta_1cost_history.append(compute_cost(x_values, y_values, theta_0, theta_1))if len(cost_history) > 1 and abs(cost_history[-1] - cost_history[-2]) < convergence_threshold:# 如果损失函数的变化小于收敛阈值,则停止迭代breakreturn theta_0, theta_1, cost_history
# 这一code block用来调用上面的函数# K值的选择需要我们不断尝试与比较,来获取更好的效果
possible_K_values = [1, 3, 4, 5, 6, 7, 10] # 可能得K值需要自己设定,对于不同的数据集,可能需要不同的K值
best_K = possible_K_values[0]
lowest_cost = float('inf')
theta_0_mini_batch = 0
theta_1_mini_batch = 0
cost_history_mini_batch = []for K in possible_K_values: # 对于每一个K值theta_0_temp, theta_1_temp, cost_history_temp = mini_batch_gradient_descent(x_values, y_values, K)if cost_history_temp[-1] < lowest_cost: # 如果损失函数的值更小lowest_cost = cost_history_temp[-1]best_K = Ktheta_0_mini_batch = theta_0_temptheta_1_mini_batch = theta_1_tempcost_history_mini_batch = cost_history_tempbest_K, theta_0_mini_batch, theta_1_mini_batch, lowest_cost
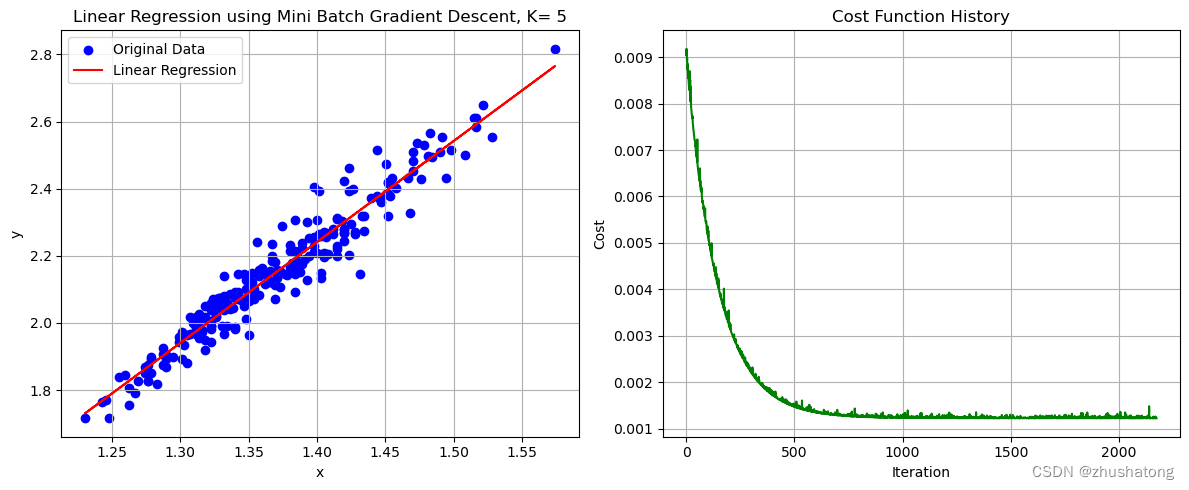
# 这一code block用来画出数据点和拟合直线
plot_data_and_line(x_values, y_values, theta_0_mini_batch, theta_1_mini_batch, cost_history_mini_batch,'Linear Regression using Mini Batch Gradient Descent, K= ' + str(best_K))
3. 自适应梯度下降法 Adagrad(在学习率方面进行了改进)
θ ( t + 1 ) : = θ ( t ) − a ∑ i = 0 t ( g ( i ) ) 2 g ( t ) \begin{aligned}\theta^{(\mathbf{t+1})}{:}=\theta^{(\mathbf{t})}-\frac{a}{\sqrt{\sum_{i=0}^{t}(g^{(i)})^2}}g^{(t)}\end{aligned} θ(t+1):=θ(t)−∑i=0t(g(i))2ag(t)
其中
g ( t ) = ∂ J ( θ ( t ) ) ∂ θ g^{(t)}=\frac{\partial J(\theta^{(t)})}{\partial\theta} g(t)=∂θ∂J(θ(t))
# 请注意这里的学习率,我将它设定的非常大,得益于adagrad的特性,我们可以使用更大的学习率
# 如果将学习率设定过小,会导致adagrad无法收敛,效果较差
# 所以,我们需要alpha也需要不断尝试与比较,来获取更好的效果
def adagrad_mini_batch_gradient_descent(x_values, y_values, batch_size=5, alpha=3, convergence_threshold=1e-8,max_iterations=10000):"""Perform mini batch gradient descent with adaptive learning rate.:param x_values: 这是一个list,包含了所有的x值:param y_values: 这是一个list,包含了所有的y值:param batch_size: 这是一个int,表示batch的大小:param alpha: 这是一个float,表示学习率:param convergence_threshold: 这是一个float,表示收敛阈值:param max_iterations: 这是一个int,表示最大迭代次数:return: 这是一个tuple,包含了theta_0, theta_1, cost_history,分别表示最终的theta_0, theta_1和损失函数的变化"""theta_0 = 0 # 初始化theta_0theta_1 = 0 # 初始化theta_1N = len(x_values)cost_history = []# 初始化sum_squared_gradients,这是用来计算学习率的sum_squared_gradients_0 = 0.0001 # 较小的值以避免被零除sum_squared_gradients_1 = 0.0001for _ in range(max_iterations):# 对数据进行随机打乱combined = list(zip(x_values, y_values)) # 将x_values和y_values打包成一个listrandom.shuffle(combined) # 对打包后的list进行随机打乱x_values[:], y_values[:] = zip(*combined) # 将打乱后的list解包赋值给x_values和y_values# Mini-batch updates# 这里的代码与batch gradient descent的代码类似,只是多了一个batch_size的参数for i in range(0, N, batch_size):x_batch = x_values[i:i + batch_size]y_batch = y_values[i:i + batch_size]sum_theta_0 = 0sum_theta_1 = 0for j in range(len(x_batch)):error = f_theta(x_batch[j], theta_0, theta_1) - y_batch[j]sum_theta_0 += errorsum_theta_1 += error * x_batch[j]# 计算梯度# 计算公式为: theta_j = theta_j - alpha / (sum_squared_gradients_j ** 0.5) * 1/N * sum((f_theta(x_i) - y_i) * x_i)gradient_0 = (1 / batch_size) * sum_theta_0 # 计算theta_0的梯度gradient_1 = (1 / batch_size) * sum_theta_1 # 计算theta_1的梯度sum_squared_gradients_0 += gradient_0 ** 2 # 更新sum_squared_gradients_0sum_squared_gradients_1 += gradient_1 ** 2 # 更新sum_squared_gradients_1adaptive_alpha_0 = alpha / (sum_squared_gradients_0 ** 0.5) # 计算theta_0的学习率adaptive_alpha_1 = alpha / (sum_squared_gradients_1 ** 0.5) # 计算theta_1的学习率theta_0 -= adaptive_alpha_0 * gradient_0 # 更新theta_0theta_1 -= adaptive_alpha_1 * gradient_1 # 更新theta_1cost_history.append(compute_cost(x_values, y_values, theta_0, theta_1))if len(cost_history) > 1 and abs(cost_history[-1] - cost_history[-2]) < convergence_threshold:# 如果损失函数的变化小于收敛阈值,则停止迭代breakreturn theta_0, theta_1, cost_history
# 这一code block用来调用上面的函数# K值的选择需要我们不断尝试与比较,来获取更好的效果
possible_K_values = [3, 4, 5, 6, 7, 10] # 可能得K值需要自己设定,对于不同的数据集,可能需要不同的K值
best_K = possible_K_values[0]
lowest_cost = float('inf')
theta_0_adaptive = 0
theta_1_adaptive = 0
cost_history_adaptive = []for K in possible_K_values: # 对于每一个K值theta_0_temp, theta_1_temp, cost_history_temp = adagrad_mini_batch_gradient_descent(x_values, y_values, K)if cost_history_temp[-1] < lowest_cost:lowest_cost = cost_history_temp[-1]best_K = Ktheta_0_adaptive = theta_0_temptheta_1_adaptive = theta_1_tempcost_history_adaptive = cost_history_tempbest_K, theta_0_adaptive, theta_1_adaptive, cost_history_adaptive[-1]
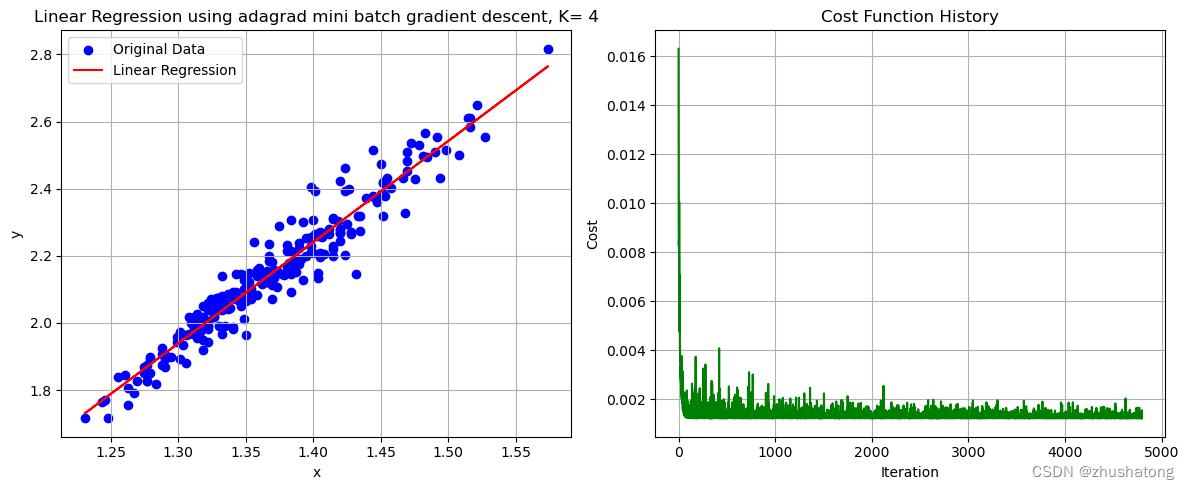
# 这一code block用来画出数据点和拟合直线
plot_data_and_line(x_values, y_values, theta_0_adaptive, theta_1_adaptive, cost_history_adaptive,'Linear Regression using adagrad mini batch gradient descent, K= ' + str(best_K))
4. 多变量线性回归 Multivariate Linear Regression(在特征方面进行了改进,拓展到多个特征)
f θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n f_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n fθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn
J ( θ 0 , θ 1 , . . . θ n ) = 1 2 N ∑ i = 1 N ( f θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1,...\theta_n)=\frac1{2N}\sum_{i=1}^N(f_\theta(x^{(i)})-y^{(i)})^2 J(θ0,θ1,...θn)=2N1i=1∑N(fθ(x(i))−y(i))2
def multivariate_gradient_descent(X, y, batch_size=5, alpha=3, convergence_threshold=1e-8, max_iterations=10000):"""Perform mini batch gradient descent with adaptive learning rate for multivariate linear regression.:param X: 这是一个矩阵,包含了所有的x值:param y: 这是一个list,包含了所有的y值:param batch_size: 这是一个int,表示batch的大小:param alpha: 这是一个float,表示学习率:param convergence_threshold: 这是一个float,表示收敛阈值:param max_iterations: 这是一个int,表示最大迭代次数:return: 这是一个tuple,包含了theta, cost_history,分别表示最终的theta和损失函数的变化,theta是一个list"""m, n = X.shape # m是样本数量,n是特征数量theta = np.zeros(n + 1) # n+1 thetas 包含 theta_0X = np.hstack((np.ones((m, 1)), X)) # 在X前面加一列1,用来计算theta_0cost_history = []sum_squared_gradients = np.zeros(n + 1) + 0.0001 # 较小的值以避免被零除for _ in range(max_iterations):# 对数据进行随机打乱indices = np.arange(m) # 生成一个0到m-1的listnp.random.shuffle(indices) # 对list进行随机打乱X = X[indices] # 用打乱后的list对X进行重新排序y = y[indices] # 用打乱后的list对y进行重新排序# Mini-batch updatesfor i in range(0, m, batch_size): # i从0开始,每次增加batch_sizeX_batch = X[i:i + batch_size] # 从i开始,取batch_size个元素y_batch = y[i:i + batch_size] # 从i开始,取batch_size个元素# 梯度计算公式为: theta_j = theta_j - alpha / (sum_squared_gradients_j ** 0.5) * 1/N * sum((f_theta(x_i) - y_i) * x_i) gradient = (1 / batch_size) * X_batch.T.dot(X_batch.dot(theta) - y_batch) # 计算梯度sum_squared_gradients += gradient ** 2 # 更新sum_squared_gradientsadaptive_alpha = alpha / np.sqrt(sum_squared_gradients) # 计算学习率theta -= adaptive_alpha * gradient # 更新thetacost = (1 / (2 * m)) * np.sum((X.dot(theta) - y) ** 2) # 计算损失函数的值cost_history.append(cost)if len(cost_history) > 1 and abs(cost_history[-1] - cost_history[-2]) < convergence_threshold:# 如果损失函数的变化小于收敛阈值,则停止迭代breakreturn theta, cost_history
# 这一code block用来调用上面的函数
# 请注意,这里的数据集是多变量线性回归的数据集
X_matrix = data[['x']].values
y_vector = data['y'].values
# best_K 已经在上面的代码中被赋值
theta_multivariate, cost_history_multivariate = multivariate_gradient_descent(X_matrix, y_vector, best_K)theta_multivariate, cost_history_multivariate[-1]
5. L1正则化 L1 Regularization(在正则化方面进行了改进)
线性回归——lasso回归和岭回归(ridge regression) - wuliytTaotao - 博客园 (cnblogs.com)
def lasso_gradient_descent(X, y, batch_size=5, lambda_=0.1, alpha=3, convergence_threshold=1e-8, max_iterations=10000):"""Perform mini batch gradient descent with adaptive learning rate and L1 regularization for multivariate linear regression."""m, n = X.shape # m是样本数量,n是特征数量theta = np.zeros(n + 1) # n+1 thetas 包含 theta_0X = np.hstack((np.ones((m, 1)), X)) # 在X前面加一列1,用来计算theta_0cost_history = []sum_squared_gradients = np.zeros(n + 1) + 0.0001 # 较小的值以避免被零除for _ in range(max_iterations):# 对数据进行随机打乱indices = np.arange(m) # 生成一个0到m-1的listnp.random.shuffle(indices) # 对list进行随机打乱X = X[indices] # 用打乱后的list对X进行重新排序y = y[indices] # 用打乱后的list对y进行重新排序# Mini-batch updatesfor i in range(0, m, batch_size): # i从0开始,每次增加batch_sizeX_batch = X[i:i + batch_size] # 从i开始,取batch_size个元素y_batch = y[i:i + batch_size] # 从i开始,取batch_size个元素# Compute gradient (including L1 penalty for j > 0)gradient = (1 / batch_size) * X_batch.T.dot(X_batch.dot(theta) - y_batch) # 计算梯度gradient[1:] += lambda_ * np.sign(theta[1:]) # 对除theta_0外的所有theta添加L1正则化sum_squared_gradients += gradient ** 2 # 更新sum_squared_gradientsadaptive_alpha = alpha / np.sqrt(sum_squared_gradients) # 计算学习率theta -= adaptive_alpha * gradient # 更新theta# Compute cost (including L1 penalty for j > 0)cost = (1 / (2 * m)) * np.sum((X.dot(theta) - y) ** 2) + lambda_ * np.sum(np.abs(theta[1:]))cost_history.append(cost)if len(cost_history) > 1 and abs(cost_history[-1] - cost_history[-2]) < convergence_threshold:# 如果损失函数的变化小于收敛阈值,则停止迭代breakreturn theta, cost_history
如何选择lambda?
def determine_best_lambda(X, y, lambdas, num_folds=5, **kwargs):"""Determine the best lambda using K-fold cross validation."""from sklearn.model_selection import KFold # 此处使用sklearn中的KFold函数,用来进行交叉验证,与线性回归无关kf = KFold(n_splits=num_folds, shuffle=True, random_state=42) # 生成交叉验证的数据,42是随机种子average_errors = [] # 用来保存每一个lambda的平均误差for lambda_ in lambdas: # 对于每一个lambdafold_errors = [] # 用来保存每一折的误差for train_index, val_index in kf.split(X):X_train, X_val = X[train_index], X[val_index] # 生成训练集和验证集y_train, y_val = y[train_index], y[val_index] # 生成训练集和验证集theta, _ = lasso_gradient_descent(X_train, y_train, lambda_=lambda_, **kwargs) # 训练模型# Compute validation errory_pred = np.hstack((np.ones((X_val.shape[0], 1)), X_val)).dot(theta) # 计算预测值error = (1 / (2 * X_val.shape[0])) * np.sum((y_pred - y_val) ** 2) # 计算误差fold_errors.append(error)average_errors.append(np.mean(fold_errors))best_lambda = lambdas[np.argmin(average_errors)] # 选择平均误差最小的lambdareturn best_lambda, average_errors
# Lambda values to test
lambdas = [0, 0.001, 0.01, 0.1, 1, 10]best_lambda, average_errors = determine_best_lambda(X_matrix, y_vector, lambdas)
best_lambda, average_errors
# Apply the multivariate gradient descent (using the single feature we have for this dataset)
X_matrix = data[['x']].values
y_vector = data['y'].values
theta_lasso, cost_history_lasso = lasso_gradient_descent(X_matrix, y_vector, best_K, best_lambda)theta_lasso, cost_history_lasso[-1]# 选择平均误差最小的lambdareturn best_lambda, average_errors
相关文章:

【机器学习】从底层手写实现线性回归
【机器学习】Building-Linear-Regression-from-Scratch 线性回归 Linear Regression0. 数据的导入与相关预处理0.工具函数1. 批量梯度下降法 Batch Gradient Descent2. 小批量梯度下降法 Mini Batch Gradient Descent(在批量方面进行了改进)3. 自适应梯度…...

判断数组中对象的某个值是否有相同的并去重
如果你想判断数组中对象的某个值是否有相同的,并进行去重,你可以使用 JavaScript 中的一些数组方法和 Set 对象。以下是一个示例: // 原始数组包含对象 const array [{ id: 1, name: John },{ id: 2, name: Jane },{ id: 3, name: Doe },{ …...

Shell脚本 变量 语句 表达式
常见的解释器 #!/bin/sh #不推荐(了解) #!/bin/bash #!/usr/bin/python #!/bin/awk#!后跟的字符表示要启动的程序,该程序读取该文件执行。 #! 是一个约定的标记,它告诉系统这个脚本需要什么解释器来执行shell 函数 myShellName () {command1 }函数调用…...
MIT6.S081-实验准备
实验全程在Vmware虚拟机 (镜像:Ubuntu-20.04-beta-desktop-amd64) 中进行 一、版本控制 1.1 将mit的实验代码克隆到本地 git clone git://g.csail.mit.edu/xv6-labs-2020 1.2 修改本地git配置文件 创建github仓库,记录仓库地址 我的仓库地址就是htt…...

工具在手,创作无忧:一键下载安装Auto CAD工具,让艺术创作更加轻松愉悦!
不要再浪费时间在网上寻找Auto CAD的安装包了!因为你所需的一切都可以在这里找到!作为全球领先的设计和绘图软件,Auto CAD为艺术家、设计师和工程师们提供了无限的创作潜力。不论是建筑设计、工业设计还是室内装饰,Auto CAD都能助…...

第25节: Vue3 带组件
在UniApp中使用Vue3框架时,你可以使用组件来封装可复用的代码块,并在需要的地方进行渲染。下面是一个示例,演示了如何在UniApp中使用Vue3框架使用带组件: <template> <view> <button click"toggleActive&q…...

ubuntu apache2配置反向代理
1.Ubuntu安装apache sudo apt-get update sudo apt-get install apache2 2.apache2反向代理配置 sudo vim /etc/apache2/sites-available/000-default.conf 添加内容如下: <VirtualHost *:80># The ServerName directive sets the request scheme, host…...

【数据挖掘 | 关联规则】FP-grow算法详解(附详细代码、案例实战、学习资源)
! 🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&a…...
 11)
力扣题目学习笔记(OC + Swift) 11
11.盛最多水的容器 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明:你不能倾…...
JVM基础入门
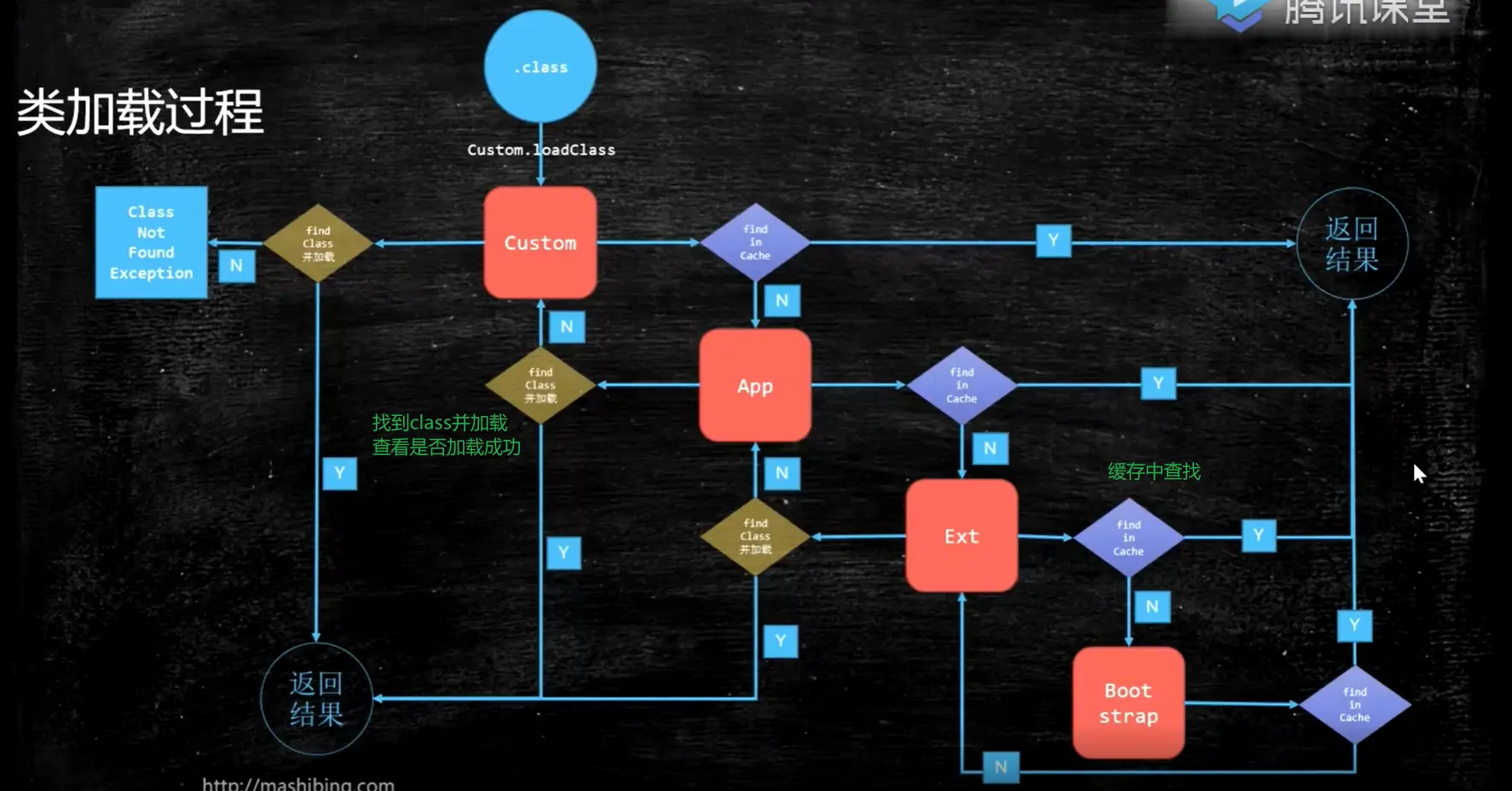
JVM 基础入门 JVM 基础 聊一聊 Java 从编码到执行到底是一个怎么样的过程? 假设我们有一个文件 x.Java,你执行 javac,它就会变成 x.class。 这个 class 怎么执行的? 当我们调用 Java 命令的时候,class 会被 load 到…...

前端真的死了吗
随着人工智能和低代码的崛起,“前端已死”的声音逐渐兴起。前端已死?尊嘟假嘟?快来发表你的看法吧! 以下方向仅供参考。 一、为什么会出现“前端已死”的言论 前端已死这个言论 是出自于2022年开始 ,2022年下半年疫情…...

前后端分离开发
前期 前后端混合开发 后期 前后端分离开发...
向量数据库——AI时代的基座
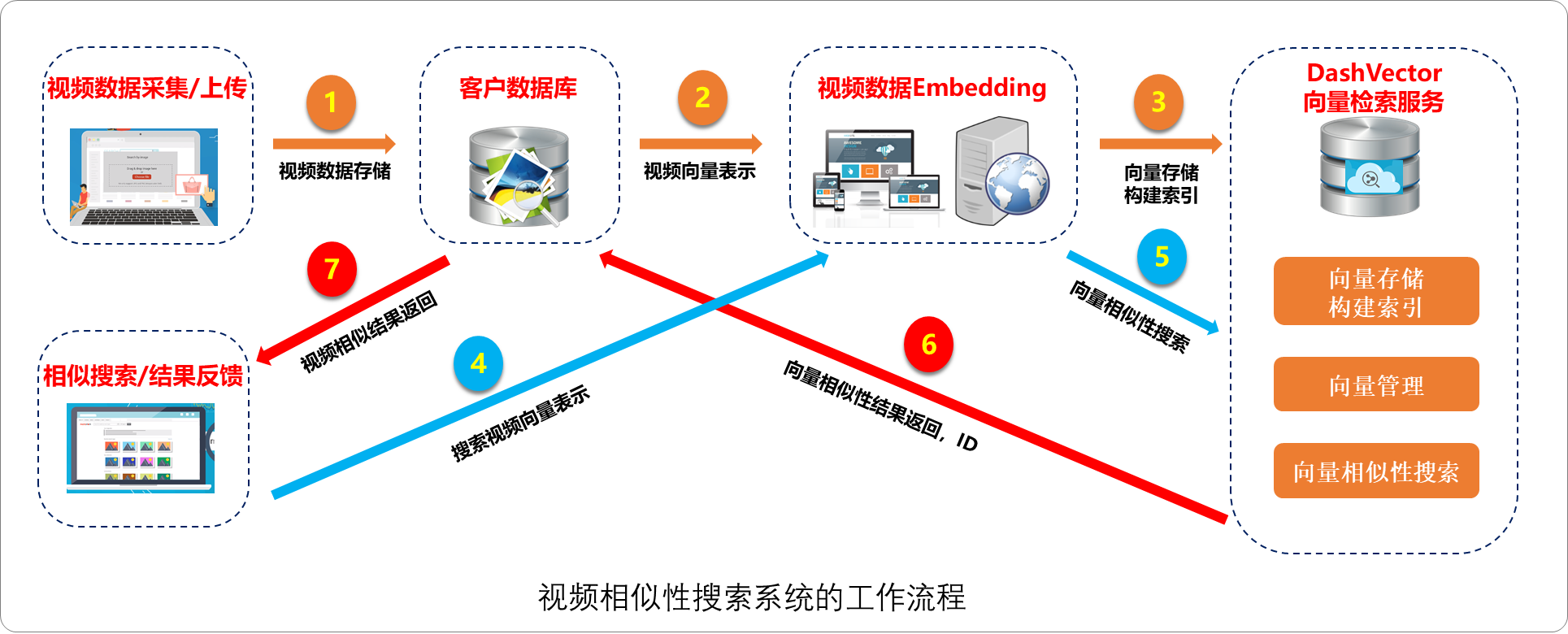
向量数据库——AI时代的基座 1.前言 向量数据库在构建基于大语言模型的行业智能应用中扮演着重要角色。大模型虽然能回答一般性问题,但在垂直领域服务中,其知识深度、准确度和时效性有限。为了解决这一问题,企业可以利用向量数据库结合大模…...

【️什么是分布式系统的一致性 ?】
😊引言 🎖️本篇博文约8000字,阅读大约30分钟,亲爱的读者,如果本博文对您有帮助,欢迎点赞关注!😊😊😊 🖥️什么是分布式系统的一致性 ?…...

鸿蒙ArkTS Web组件加载空白的问题原因及解决方案
问题症状 初学鸿蒙开发,按照官方文档Web组件文档《使用Web组件加载页面》示例中的代码照抄运行后显示空白,纠结之余多方搜索后扔无解决方法。 运行代码 import web_webview from ohos.web.webviewEntry Component struct Index {controller: web_webv…...
【Java】网络编程-UDP回响服务器客户端简单代码编写
这一篇文章我们将讲述网络编程中UDP服务器客户端的编程代码 1、前置知识 UDP协议全称是用户数据报协议,在网络中它与TCP协议一样用于处理数据包,是一种无连接的协议。 UDP的特点有:无连接、尽最大努力交付、面向报文、没有拥塞控制 本文讲…...

【设计模式】之工厂模式
工厂模式 1.介绍 工厂模式(创建型模式),是我们最常用的实例化对象模式,是用工厂方法代替new操作的一种模式;在工厂模式中,我们在创建对象时不会对客户端暴露创建逻辑,并且是通过使用一个共同的…...

70.爬楼梯
题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 注意: 给定 n 是一个正整数。 示例 1: 输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶…...

【论文解读】ICLR 2024高分作:ViT需要寄存器
来源:投稿 作者:橡皮 编辑:学姐 论文链接:https://arxiv.org/abs/2309.16588 摘要: Transformer最近已成为学习视觉表示的强大工具。在本文中,我们识别并表征监督和自监督 ViT 网络的特征图中的伪影。这些…...
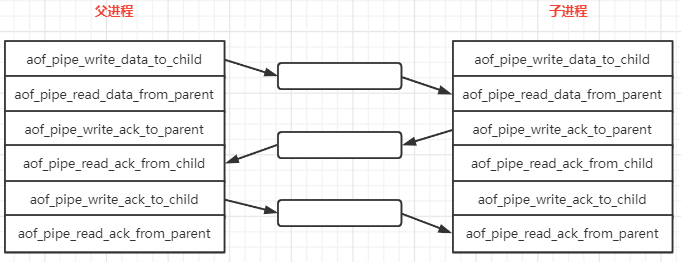
【Redis】AOF 基础
因为 Redis AOF 的实现有些绕, 就分成 2 篇进行分析, 本篇主要是介绍一下 AOF 的一些特性和依赖的其他函数的逻辑,为下一篇 (Redis AOF 源码) 源码分析做一些铺垫。 AOF 全称: Append Only File, 是 Redis 提供了一种数据保存模式, Redis 默认不开启。 AOF 采用日志的形式来记…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
