二叉搜索树的简单C++类实现
二叉搜索树(BST)是一种重要的数据结构,它对于理解树的操作和算法至关重要,其中序输出是有序的。本文通过C++实现一个BST的类,并在插入和删除节点时提供清晰的输出,可视化这些操作的过程。
二叉搜索树的节点结构
首先定义一个TreeNode结构来表示树中的每个节点。每个节点包含一个整数值、一个指向左子节点的指针和一个指向右子节点的指针。
struct TreeNode {int value;TreeNode *left;TreeNode *right;TreeNode(int x) : value(x), left(nullptr), right(nullptr) {}
};
二叉搜索树类的实现
创建了一个BinarySearchTree类,它包含一个指向树根的指针和几个私有的递归辅助函数。这些函数用于实现插入、中序遍历和删除整棵树的操作。
class BinarySearchTree {
private:TreeNode *root;// 递归帮助函数,用于插入值TreeNode* insert(TreeNode *node, int value) {if (node == nullptr) {std::cout << "Inserted " << value << " into the BST.\n";return new TreeNode(value);}if (value < node->value) {std::cout << "Inserting " << value << " to the left of " << node->value << ".\n";node->left = insert(node->left, value);} else if (value > node->value) {std::cout << "Inserting " << value << " to the right of " << node->value << ".\n";node->right = insert(node->right, value);}return node;}// 递归帮助函数,用于中序遍历void inorderTraversal(TreeNode *node) const {if (node != nullptr) {inorderTraversal(node->left);std::cout << node->value << " ";inorderTraversal(node->right);}}// 递归帮助函数,用于删除树void deleteTree(TreeNode *node) {if (node != nullptr) {deleteTree(node->left);deleteTree(node->right);std::cout << "Deleting node with value: " << node->value << "\n";delete node;}}public:BinarySearchTree() : root(nullptr) {}~BinarySearchTree() {deleteTree(root);}void insert(int value) {root = insert(root, value);}void inorderTraversal() const {std::cout << "Inorder Traversal: ";inorderTraversal(root);std::cout << std::endl;}
};
插入操作
在insert函数中添加打印语句来显示插入过程。这些打印语句帮助我们可视化了插入的每一步。
中序遍历
中序遍历是一种遍历树的方法,它首先访问左子树,然后访问根节点,最后访问右子树。对于BST来说,中序遍历的结果是按排序顺序显示树中的所有值。
删除操作
在BinarySearchTree的析构函数中,我们实现了deleteTree函数来删除整棵树。在删除每个节点之前,我们打印出该节点的值。
主函数
在主函数中,我们创建了一个二叉搜索树实例,并插入了一些值。然后,我们执行了中序遍历来查看树的内容。
int main() {BinarySearchTree bst;// 插入元素bst.insert(5);bst.insert(3);bst.insert(7);bst.insert(2);bst.insert(4);bst.insert(6);bst.insert(8);// 中序遍历二叉搜索树bst.inorderTraversal();return 0;
}
结果分析
当我们运行上述程序时,控制台输出显示了插入节点的过程,并在程序结束时显示了删除节点的过程。
Inserted 5 into the BST.
Inserting 3 to the left of 5.
Inserted 3 into the BST.
Inserting 7 to the right of 5.
Inserted 7 into the BST.
Inserting 2 to the left of 5.
Inserting 2 to the left of 3.
Inserted 2 into the BST.
Inserting 4 to the left of 5.
Inserting 4 to the right of 3.
Inserted 4 into the BST.
Inserting 6 to the right of 5.
Inserting 6 to the left of 7.
Inserted 6 into the BST.
Inserting 8 to the right of 5.
Inserting 8 to the right of 7.
Inserted 8 into the BST.
Inorder Traversal: 2 3 4 5 6 7 8
Deleting node with value: 2
Deleting node with value: 4
Deleting node with value: 3
Deleting node with value: 6
Deleting node with value: 8
Deleting node with value: 7
Deleting node with value: 5
通过这些输出可以清楚地看到二叉搜索树在插入和删除节点时的行为。
不过要注意,这个示例没有实现删除单个节点的功能。在实际应用中,删除操作通常需要考虑多种不同的情况,并且可能需要重新平衡树以保持其性能。
相关文章:

二叉搜索树的简单C++类实现
二叉搜索树(BST)是一种重要的数据结构,它对于理解树的操作和算法至关重要,其中序输出是有序的。本文通过C实现一个BST的类,并在插入和删除节点时提供清晰的输出,可视化这些操作的过程。 二叉搜索树的节点结…...

禁毒知识竞赛流程和规则
禁毒知识竞赛是一项全国性竞赛活动。有着深化全国青少年毒品预防教育,巩固学校毒品预防教育成果的重要作用。本文介绍一场禁毒知识竞赛的完整流程和规则,供单位组织此类活动时参考。 1、赛制 第一轮10进6,第二轮6进4,4支队伍决出…...

CSS 基础
文章目录 CSS 常见的属性CSS 常见样式行内样式内嵌样式导入样式 CSS 选择器标签选择器id选择器类选择器全局选择器属性选择器组合选择器 CSS 常见应用表格列表导航栏下拉菜单提示工具图片廊 CSS (Cascading Style Sheets,层叠样式表),是一种用…...

黑色翻页时钟HTML源码-倒计时单页翻页时钟
黑色翻页时钟HTML源码-倒计时单页翻页时钟这是一个类似fliqlo的黑色翻页时钟HTML源码,它仅包含一个HTML文件,上传到网站后即可使用。该时钟具有查看当前时间、秒表和倒计时功能,并且可以在页面的右下角进行设置。 红色动态炫酷数字时钟html网…...
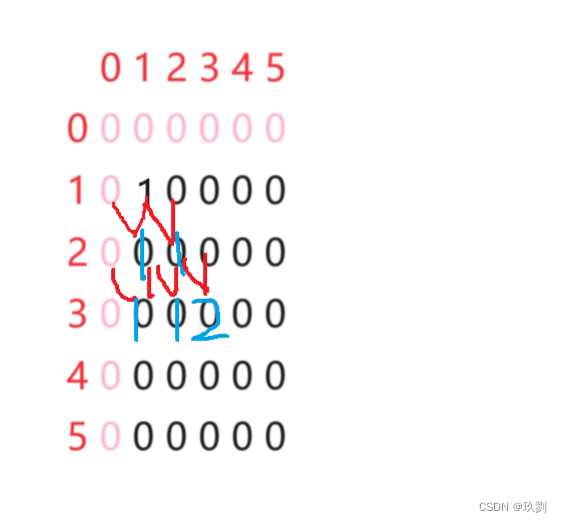
2043杨辉三角(C语言)
目录 一:题目 二:思路分析 三:代码 一:题目 二:思路分析 1.通过杨辉三角,不难发现中间的数等于肩头两个数之和 2.但是当我们的输出结果,与杨辉三角的形式有所不同,但是我们可以找…...
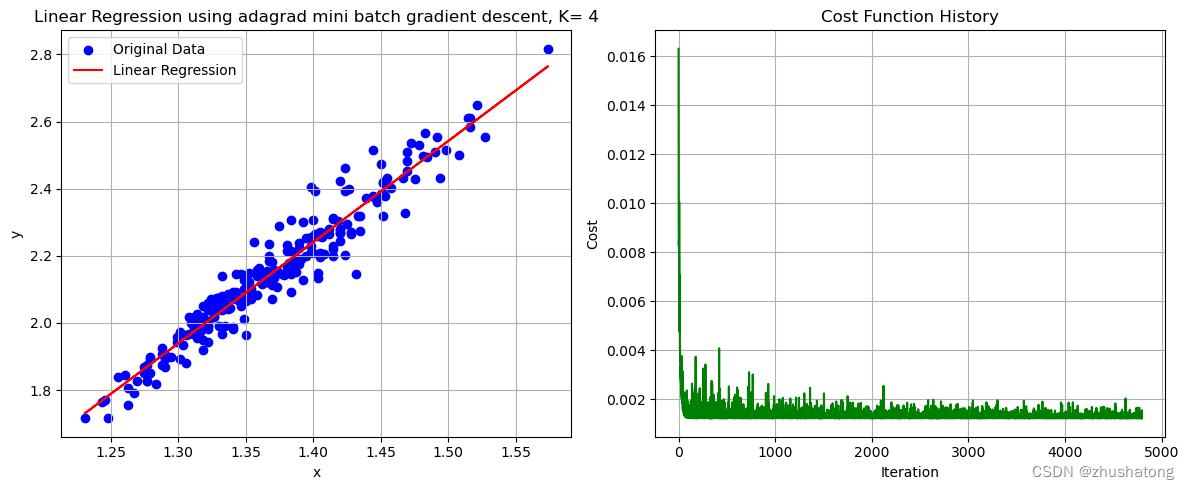
【机器学习】从底层手写实现线性回归
【机器学习】Building-Linear-Regression-from-Scratch 线性回归 Linear Regression0. 数据的导入与相关预处理0.工具函数1. 批量梯度下降法 Batch Gradient Descent2. 小批量梯度下降法 Mini Batch Gradient Descent(在批量方面进行了改进)3. 自适应梯度…...

判断数组中对象的某个值是否有相同的并去重
如果你想判断数组中对象的某个值是否有相同的,并进行去重,你可以使用 JavaScript 中的一些数组方法和 Set 对象。以下是一个示例: // 原始数组包含对象 const array [{ id: 1, name: John },{ id: 2, name: Jane },{ id: 3, name: Doe },{ …...

Shell脚本 变量 语句 表达式
常见的解释器 #!/bin/sh #不推荐(了解) #!/bin/bash #!/usr/bin/python #!/bin/awk#!后跟的字符表示要启动的程序,该程序读取该文件执行。 #! 是一个约定的标记,它告诉系统这个脚本需要什么解释器来执行shell 函数 myShellName () {command1 }函数调用…...
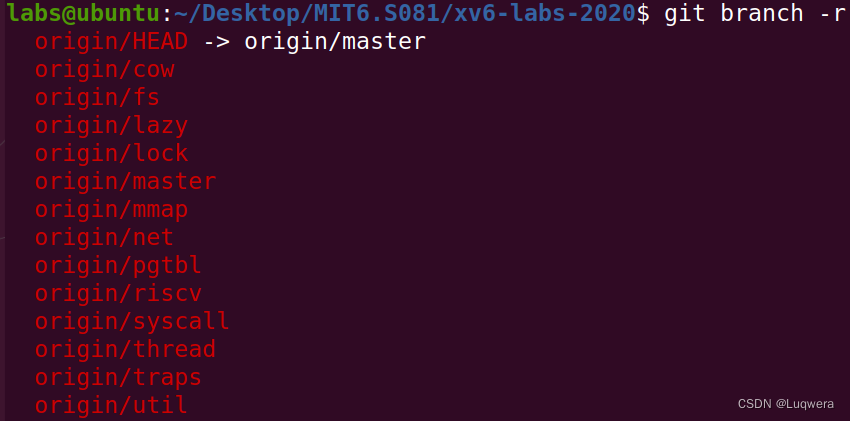
MIT6.S081-实验准备
实验全程在Vmware虚拟机 (镜像:Ubuntu-20.04-beta-desktop-amd64) 中进行 一、版本控制 1.1 将mit的实验代码克隆到本地 git clone git://g.csail.mit.edu/xv6-labs-2020 1.2 修改本地git配置文件 创建github仓库,记录仓库地址 我的仓库地址就是htt…...

工具在手,创作无忧:一键下载安装Auto CAD工具,让艺术创作更加轻松愉悦!
不要再浪费时间在网上寻找Auto CAD的安装包了!因为你所需的一切都可以在这里找到!作为全球领先的设计和绘图软件,Auto CAD为艺术家、设计师和工程师们提供了无限的创作潜力。不论是建筑设计、工业设计还是室内装饰,Auto CAD都能助…...

第25节: Vue3 带组件
在UniApp中使用Vue3框架时,你可以使用组件来封装可复用的代码块,并在需要的地方进行渲染。下面是一个示例,演示了如何在UniApp中使用Vue3框架使用带组件: <template> <view> <button click"toggleActive&q…...

ubuntu apache2配置反向代理
1.Ubuntu安装apache sudo apt-get update sudo apt-get install apache2 2.apache2反向代理配置 sudo vim /etc/apache2/sites-available/000-default.conf 添加内容如下: <VirtualHost *:80># The ServerName directive sets the request scheme, host…...

【数据挖掘 | 关联规则】FP-grow算法详解(附详细代码、案例实战、学习资源)
! 🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&a…...
 11)
力扣题目学习笔记(OC + Swift) 11
11.盛最多水的容器 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明:你不能倾…...
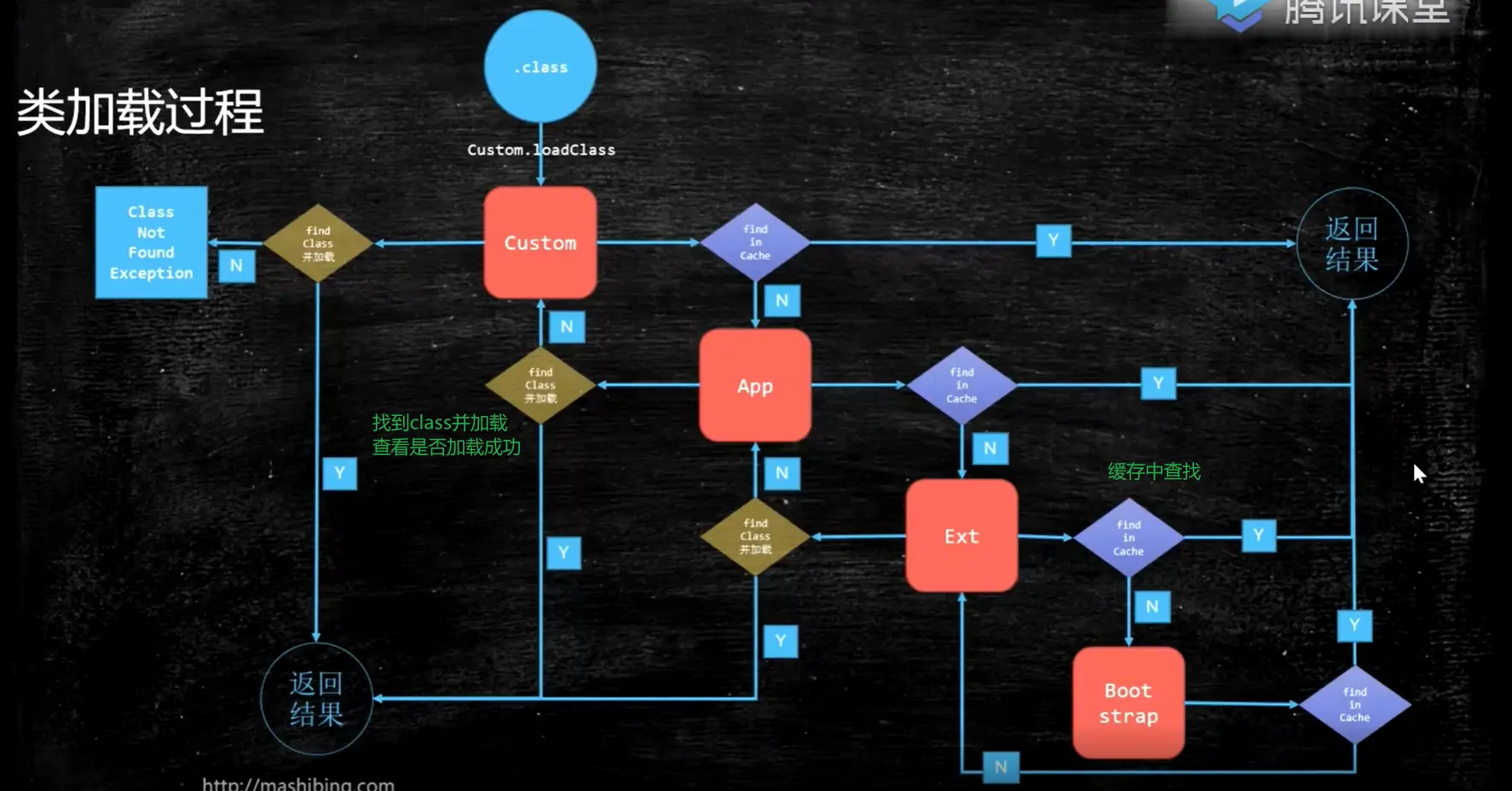
JVM基础入门
JVM 基础入门 JVM 基础 聊一聊 Java 从编码到执行到底是一个怎么样的过程? 假设我们有一个文件 x.Java,你执行 javac,它就会变成 x.class。 这个 class 怎么执行的? 当我们调用 Java 命令的时候,class 会被 load 到…...

前端真的死了吗
随着人工智能和低代码的崛起,“前端已死”的声音逐渐兴起。前端已死?尊嘟假嘟?快来发表你的看法吧! 以下方向仅供参考。 一、为什么会出现“前端已死”的言论 前端已死这个言论 是出自于2022年开始 ,2022年下半年疫情…...

前后端分离开发
前期 前后端混合开发 后期 前后端分离开发...
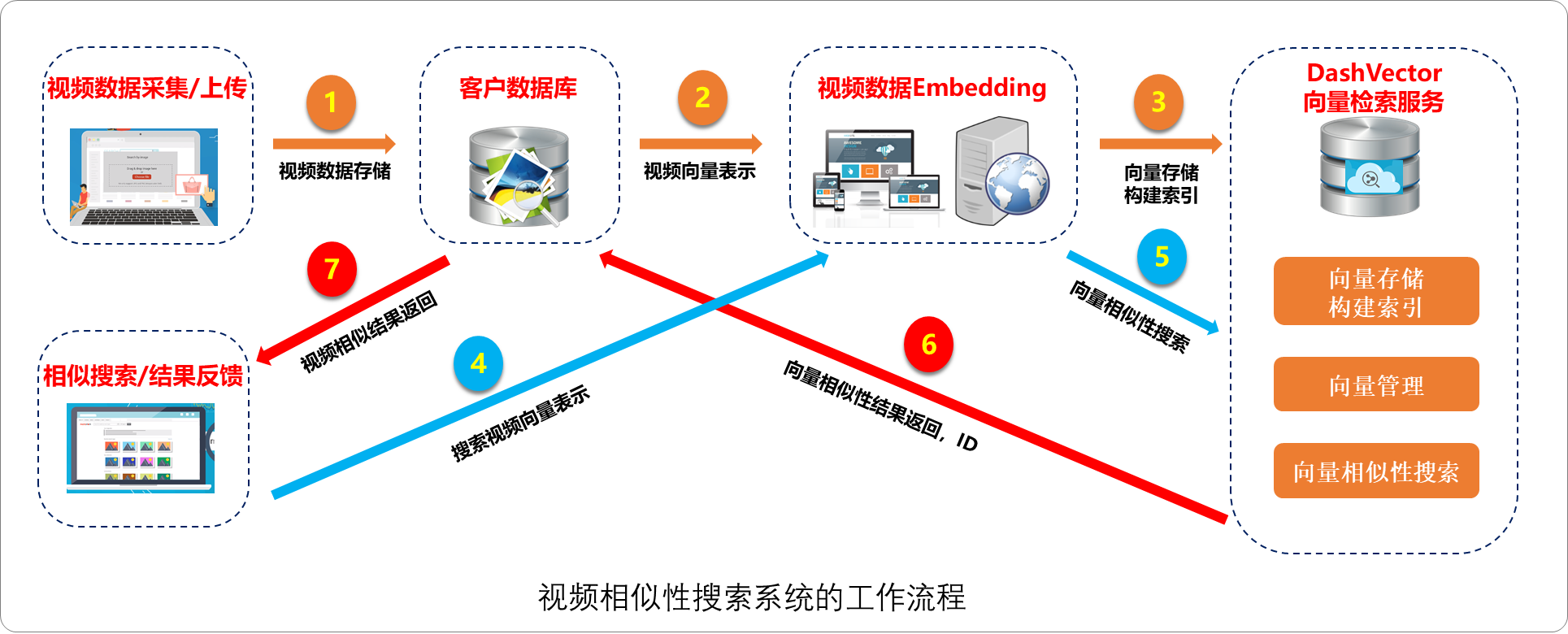
向量数据库——AI时代的基座
向量数据库——AI时代的基座 1.前言 向量数据库在构建基于大语言模型的行业智能应用中扮演着重要角色。大模型虽然能回答一般性问题,但在垂直领域服务中,其知识深度、准确度和时效性有限。为了解决这一问题,企业可以利用向量数据库结合大模…...

【️什么是分布式系统的一致性 ?】
😊引言 🎖️本篇博文约8000字,阅读大约30分钟,亲爱的读者,如果本博文对您有帮助,欢迎点赞关注!😊😊😊 🖥️什么是分布式系统的一致性 ?…...

鸿蒙ArkTS Web组件加载空白的问题原因及解决方案
问题症状 初学鸿蒙开发,按照官方文档Web组件文档《使用Web组件加载页面》示例中的代码照抄运行后显示空白,纠结之余多方搜索后扔无解决方法。 运行代码 import web_webview from ohos.web.webviewEntry Component struct Index {controller: web_webv…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
