动态规划(Dynamic Programming)
动态规划(Dynamic Programming):是运筹学的一种最优化方法,只不过在计算机问题上应用比较多
DP常见步骤:
- 暴力递归/穷举
- 记忆化搜索(傻缓存 + 递归),使用备忘录/ DP Table 来优化穷举过程
- 严格表结构(整理缓存之间的关系,如dp[i] = dp[i - 1])
例子
509.斐波那契数

1.暴力递归
int fib(int N) {if (N == 1 || N == 2){return 1;}return fib(N - 1) + fib(N - 2);
}2.记忆化搜索(加缓存)
int fib(int N) {// 备忘录全初始化为 0int[] memo = new int[N + 1];// 进行带备忘录的递归return dp(memo, N);
}// 带着备忘录进行递归
int dp(int[] memo, int n) {// base caseif (n == 0 || n == 1) return n;// 已经计算过,不用再计算了if (memo[n] != 0) return memo[n];memo[n] = dp(memo, n - 1) + dp(memo, n - 2);return memo[n];
}
3.严格表结构(缓存+状态转移方程)
int fib(int N) {if (N == 0) return 0;int[] dp = new int[N + 1];// base casedp[0] = 0; dp[1] = 1;// 状态转移for (int i = 2; i <= N; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[N];
}
4.空间压缩(优化)
由 状态转移方程可知,f(n) 只和 f(n-1) 和 f(n-2) 有关,使用「滚动数组思想」可以把空间复杂度优化成 O(1)
int fib(int n) {if (n < 2) {return n;}int p = 0, q = 0, r = 1;for (int i = 2; i <= n; ++i) {p = q; q = r; r = p + q;}return r;}
基础类DP
70.爬楼梯

经典动态规划
class Solution {public int climbStairs(int n) {if (n == 1){return 1;}int[] dp = new int[n + 1];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}空间压缩
class Solution {public int climbStairs(int n) {if (n == 1) {return 1;}int prev = 1;int cur = 2;int next = 0;for (int i = 3; i <= n; i++) {next = cur + prev;prev = cur;cur = next;}return cur;}
}746.使用最小花费爬楼梯

class Solution {public int minCostClimbingStairs(int[] cost) {int[] dp = new int[cost.length + 2];dp[1] = 0;dp[2] = 0;for (int i = 3; i <= cost.length + 1; i++) {dp[i] = Math.min(dp[i - 1] + cost[i - 2], dp[i - 2] + cost[i - 3]);}return dp[cost.length + 1];}
}空间压缩
class Solution {public int minCostClimbingStairs(int[] cost) {int prev = 0;int cur = 0;int next = 0;for (int i = 2; i <= cost.length; i++) {next = Math.min(prev + cost[i - 2], cur + cost[i - 1]);prev = cur;cur = next;}return cur;}
}62.不同路径

class Solution {public int uniquePaths(int m, int n) {if (m <= 0 || n <= 0) {return 0;}int[][] dp = new int[m][n];// base casefor (int i = 0; i < m; i++) {dp[i][0] = 1;}for (int i = 0; i < n; i++) {dp[0][i] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
}路径压缩
class Solution {public int uniquePaths(int m, int n) {if (m <= 0 || n <= 0) {return 0;}int[] dp = new int[n];// base caseArrays.fill(dp, 1);for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[j] += dp[j - 1];}}return dp[n - 1];}
}63.不同路径 II
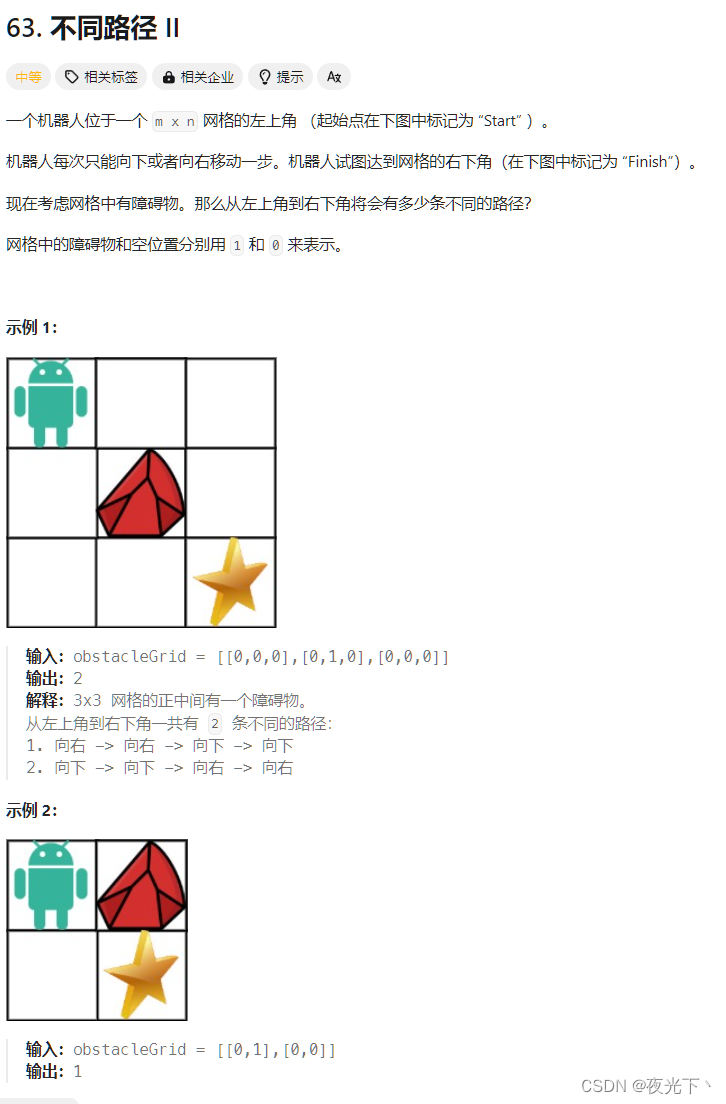
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int row = obstacleGrid.length;int col = obstacleGrid[0].length;int[][] dp = new int[row][col];for (int i = 0; i < row; i++) {if (obstacleGrid[i][0] == 1){break;}dp[i][0] = 1;}for (int i = 0; i < col; i++) {if (obstacleGrid[0][i] == 1){break;}dp[0][i] = 1;}for (int i = 1; i < row; i++) {for (int j = 1; j < col; j++) {dp[i][j] = obstacleGrid[i][j] == 1 ? 0 : dp[i - 1][j] + dp[i][j - 1];}}return dp[row - 1][col - 1];}
}空间压缩
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int row = obstacleGrid.length;int col = obstacleGrid[0].length;if (obstacleGrid[0][0] == 1 || obstacleGrid[row - 1][col - 1] == 1) {return 0;}int[] dp = new int[col];dp[0] = 1;for (int j = 1; j < col; j++) {if (obstacleGrid[0][j] == 1) {break;}dp[j] = 1;}for (int i = 1; i < row; i++) {dp[0] = (obstacleGrid[i][0] == 1 || dp[0] == 0) ? 0 : 1;for (int j = 1; j < col; j++) {dp[j] = obstacleGrid[i][j] == 1 ? 0 : dp[j] + dp[j - 1];}}return dp[col - 1];}
}64.最小路径和

class Solution {public int minPathSum(int[][] grid) {int row = grid.length;int col = grid[0].length;int[][] dp = new int[row][col];dp[0][0] = grid[0][0];for (int i = 1; i < row; i++) {dp[i][0] = grid[i][0] + dp[i - 1][0];}for (int i = 1; i < col; i++) {dp[0][i] = grid[0][i] + dp[0][i - 1];}for (int i = 1; i < row; i++) {for (int j = 1; j < col; j++) {dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];}}return dp[row - 1][col - 1];}
}空间压缩
class Solution {public int minPathSum(int[][] grid) {int row = grid.length;int col = grid[0].length;int[] dp = new int[col];dp[0] = grid[0][0];for (int i = 1; i < col; i++) {dp[i] = grid[0][i] + dp[i - 1];}for (int i = 1; i < row; i++) {dp[0] = dp[0] + grid[i][0];for (int j = 1; j < col; j++) {dp[j] = Math.min(dp[j], dp[j - 1]) + grid[i][j];}}return dp[col - 1];}
}0-1背包类DP

在上述例题中,由于每个物体只有两种可能的状态(取与不取),对应二进制中的0和1,这类问题便被称为「0-1 背包问题」。

- 01背包最重要的是如何识别出来为01背包,一般是有一个目标堆,对于数组的元素有留和舍两种选择,通过数组值的取舍进行达到目标堆的目的
- 背包问题进行空间压缩时,weight 的循环要从大到小遍历,否则会造成前段值覆盖引起的答案错误。
416.分割等和子集

class Solution {public boolean canPartition(int[] nums) {int sum = 0;int max = 0;for (int num : nums) {sum += num;max = Math.max(max, num);}int half = sum / 2;if (((sum & 1) == 1) || max > half){return false;}boolean[][] dp = new boolean[nums.length][half + 1];// base casedp[0][0] = true; // 第一个元素不选,容量为0时满足的dp[0][nums[0]] = true; // 选择第一个元素for (int i = 1; i < nums.length; i++) {for (int j = 1; j <= half; j++) {// 不选择 num[i]dp[i][j] = dp[i-1][j];// 保证下标不越界if (j - nums[i] >= 0){// 选择 num[i], 看是否能在 [0, i - 1] 这个子区间内找到一部分元素,使得它们的和为 j - nums[i]dp[i][j] |= dp[i - 1][j - nums[i]];}}// 由于状态转移方程的特殊性,提前结束,可以认为是剪枝操作if (dp[i][half]) {return true;}}return dp[nums.length - 1][half];}
}空间压缩
class Solution {public boolean canPartition(int[] nums) {int sum = 0;int max = 0;for (int num : nums) {sum += num;max = Math.max(max, num);}int half = sum / 2;if (((sum & 1) == 1) || max > half) {return false;}boolean[] dp = new boolean[half + 1];dp[0] = true;for (int i = 1; i < nums.length; i++) {for (int j = half; j >= nums[i]; j--) {dp[j] |= dp[j - nums[i]];}if (dp[half]) {return true;}}return dp[half];}
}494.目标和

class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int num : nums) {sum += num;}if (Math.abs(sum) < Math.abs(target)) {return 0;}// 因为包含了负数和 0, range: [-sum, sum]int range = 2 * sum + 1;int[][] dp = new int[nums.length][range];dp[0][sum - nums[0]] += 1;dp[0][sum + nums[0]] += 1;for (int i = 1; i < nums.length; i++) {for (int j = -sum; j <= sum; j++) {if (j + nums[i] > sum) { // 超过 [-sum, sum] 的范围,只能减dp[i][j + sum] = dp[i - 1][j - nums[i] + sum];} else if (j - nums[i] < -sum) { // 超过 [-sum, sum] 的范围,只能加dp[i][j + sum] = dp[i - 1][j + nums[i] + sum];} else {dp[i][j + sum] = dp[i - 1][j - nums[i] + sum] + dp[i - 1][j + nums[i] + sum];}}}return dp[nums.length - 1][sum + target];}
}474.一和零

class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][][] dp = new int[strs.length + 1][m + 1][n + 1];for (int i = 1; i <= strs.length; i++) {int zeros = containsZero(strs[i - 1]);int ones = strs[i - 1].length() - zeros;for (int j = 0; j <= m; j++) {for (int k = 0; k <= n; k++) {dp[i][j][k] = dp[i - 1][j][k];if (j >= zeros && k >= ones){dp[i][j][k] = Math.max(dp[i][j][k], dp[i - 1][j - zeros][k - ones] + 1);}}}}return dp[strs.length][m][n];}private int containsZero(String str) {int res = 0;for (char c : str.toCharArray()) {if (c == '0') {res++;}}return res;}
}空间压缩
class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp = new int[m + 1][n + 1];for (int i = 1; i <= strs.length; i++) {int zeros = containsZero(strs[i - 1]);int ones = strs[i - 1].length() - zeros;for (int j = m; j >= 0; j--) {for (int k = n; k >= 0; k--) {if (j >= zeros && k >= ones){dp[j][k] = Math.max(dp[j][k], dp[j - zeros][k - ones] + 1);}}}}return dp[m][n];}private int containsZero(String str) {int res = 0;for (char c : str.toCharArray()) {if (c == '0') {res++;}}return res;}
}相关文章:

动态规划(Dynamic Programming)
动态规划(Dynamic Programming):是运筹学的一种最优化方法,只不过在计算机问题上应用比较多 DP常见步骤: 暴力递归/穷举记忆化搜索(傻缓存 递归),使用备忘录/ DP Table 来优化穷举过程严格表结…...
linux使用文件描述符0、1和2来处理输入和输出
文件描述符012 在Linux中,文件描述符0、1和2分别代表标准输入(stdin)、标准输出(stdout)和标准错误(stderr)。它们用于处理进程的输入和输出。 文件描述符0(stdin)&…...

how to write and run .ps1
use .txt filechange the suffix to .ps1 from .txt 3)how to run .ps1 3.1) PS D:> .\test.ps1 1 2 3 4 5 6 7 8 9 10 3.2) PS D:> tes then press tab key to compensate and complete the whole file name...

如何在PHP中处理跨域请求?
在 PHP 中处理跨域请求(CORS,Cross-Origin Resource Sharing),通常需要在服务器端设置相应的 HTTP 头,以允许来自其他域的请求。以下是一些处理跨域请求的方法: 设置 HTTP 头: 在服务器端&#…...

spring boot 配置多数据源 踩坑 BindingException: Invalid bound statement (not found)
在上一篇:《【已解决】Spring Boot多数据源的时候,mybatis报错提示:Invalid bound statement (not found)》 凯哥(凯哥Java) 已经接受了,在Spring Boot配置多数据源时候,因为自己马虎,导致的一个坑。下面&a…...
【产品】Axure的基本使用(二)
文章目录 一、元件基本介绍1.1 概述1.2 元件操作1.3 热区的使用 二、表单型元件的使用2.1 文本框2.2 文本域2.3 下拉列表2.4 列表框2.5 单选按钮2.6 复选框2.7 菜单与表格元件的使用 三、实例3.1 登录2.2 个人简历 一、元件基本介绍 1.1 概述 在Axure RP中,元件是…...

Python语言学习笔记之十(字符串处理)
本课程对于有其它语言基础的开发人员可以参考和学习,同时也是记录下来,为个人学习使用,文档中有此不当之处,请谅解。 字符串处理:以实现字符串的分割、替换、格式化、大小写转换,Python字符串处理是指对Py…...

WPF-附加属性《十二》
非常重要 依赖属性和附加属性,两者是有关系的,也是有些区别的,很多时候,可能会把两者混淆了。 附加属性(Attach Property) 顾名思义,就是附加上面的属性,自身是没有的,…...
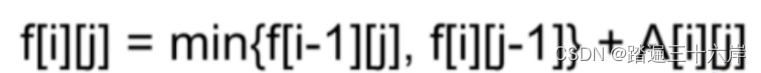
算法通关第十九关-青铜挑战理解动态规划
大家好我是苏麟 , 今天聊聊动态规划 . 动态规划是最热门、最重要的算法思想之一,在面试中大量出现,而且题目整体都偏难一些对于大部人来说,最大的问题是不知道动态规划到底是怎么回事。很多人看教程等,都被里面的状态子问题、状态…...
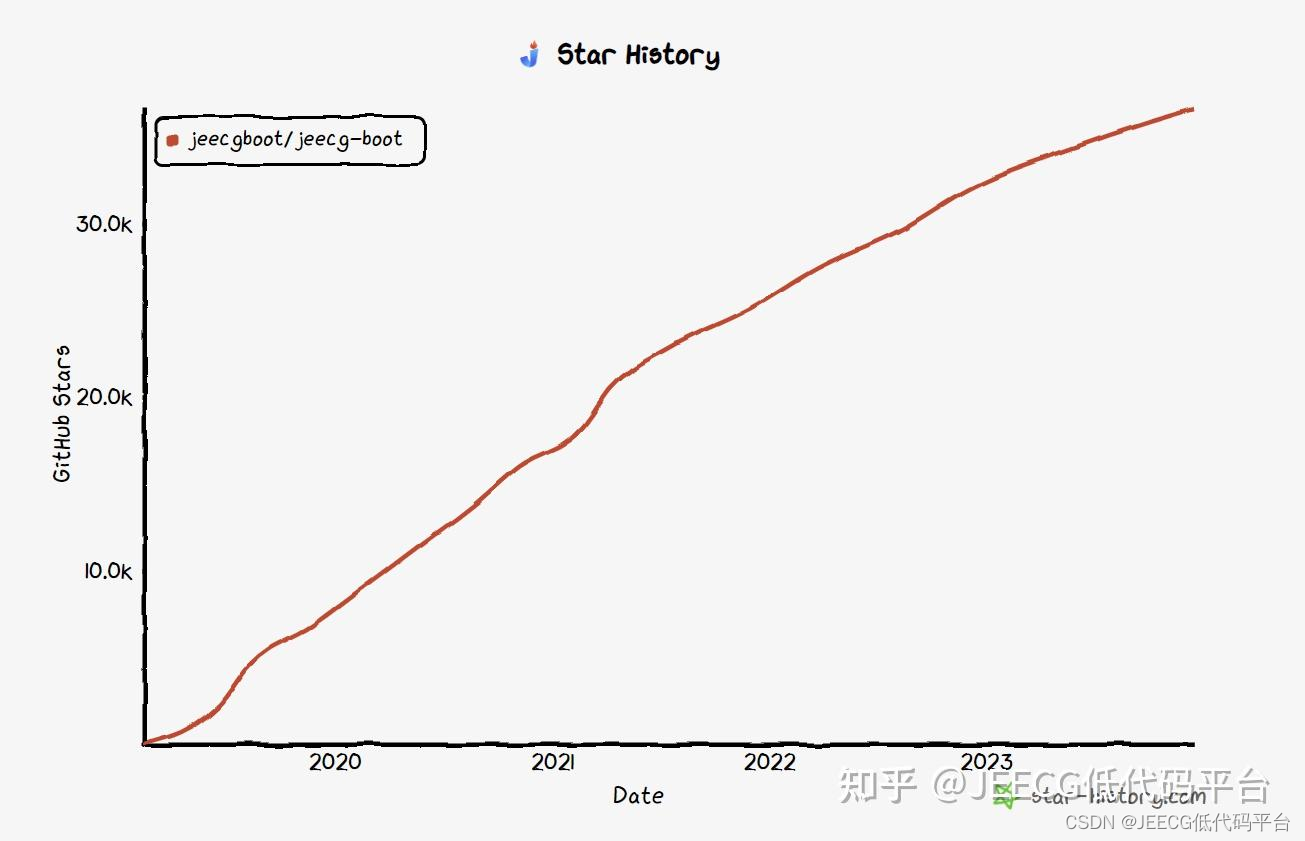
2023 GitHub年度排行榜,JEECG上榜第三名,势头依然很猛~
2023 GitHub年度排行榜TOP10,JeecgBoot上榜第三名,势头依然很猛~...
由@EnableWebMvc注解引发的Jackson解析异常
同事合了代码到开发分支,并没有涉及到改动的类却报错。错误信息如下: Servlet.service() for servlet [dispatcherServlet] in context with path [] threw exception [Request processing failed; nested exception is org.springframework.http.conv…...

ce从初阶到大牛--函数
1、显示/etc/passwd文件中以bash结尾的行; grep "bash$" /etc/passwd2、找出/etc/passwd文件中的三位或四位数; grep -E \b[0-9]{3,4}\b /etc/passwd3、找出/etc/grub2.cfg文件中,以至少一个空白字符开头,后面又跟了非…...

Java学习异常类
1 定义 异常就是指程序运行时可能出现的一些错误,例如数组越界、除零等。 我们也可以把自己觉得不合理的结果定义为“异常” 2 异常与错误 3 Java中的异常处理 catch语句:对异常的处理语句放在 catch部分,可以包含多个catch语句,…...
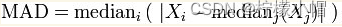
Python 全栈体系【四阶】(六)
第四章 机器学习 五、线性模型 1. 概述 线性模型是自然界最简单的模型之一,它描述了一个(或多个)自变量对另一个因变量的影响是呈简单的比例、线性关系。例如: 住房每平米单价为 1 万元,100 平米住房价格为 100 万…...
函数中学习函数的设计思想)
从memcpy()函数中学习函数的设计思想
memcpy()函数:可以理解为内存拷贝。 他的函数定义如下的 my_memcpy()函数相同。 下面这个函数是我的模拟实现,现在让我们一起来学习一下这个函数的设计思想: void * my_memcpy(void * des, const void* src, size_t size) {void * p des;…...
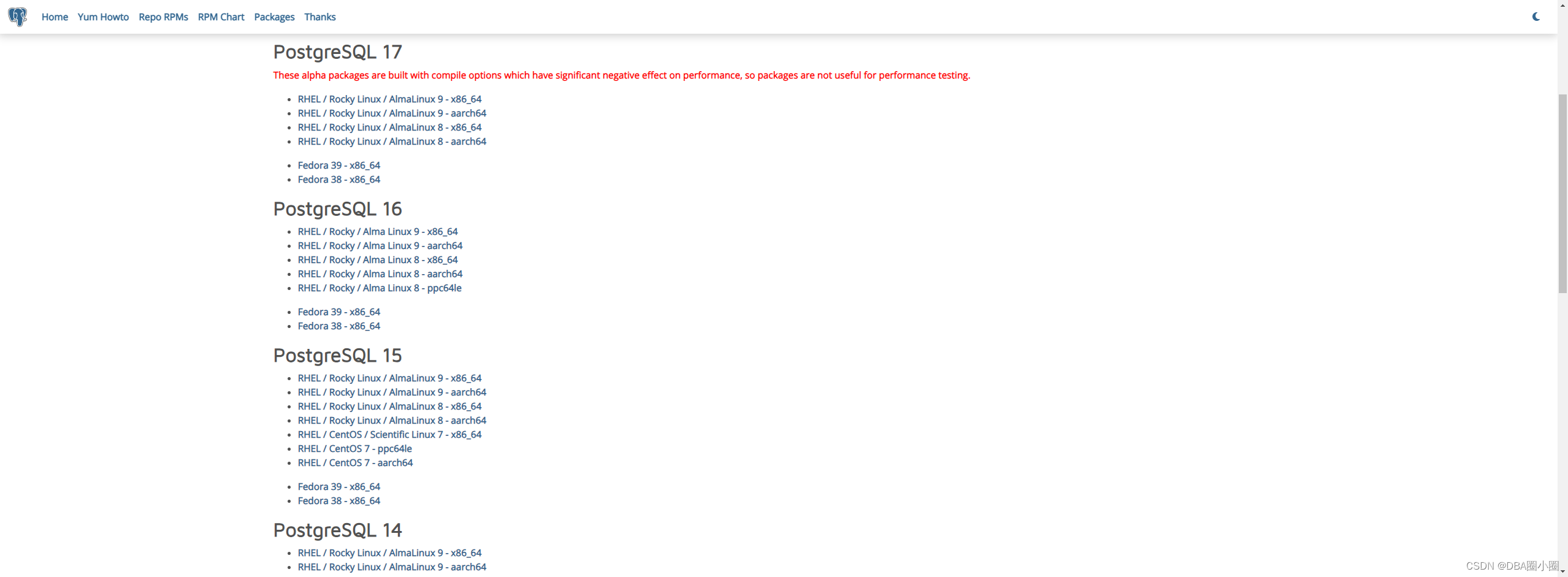
【PostgreSQL】从零开始:(二)PostgreSQL下载与安装
【PostgreSQL】从零开始:(二)PostgreSQL下载与安装 Winodws环境下载与安装PostgreSQL下载PostgreSQL安装PostgreSQL1.登录数据库2.查看下我们已有的数据库 Liunx环境下载与安装PostgreSQL使用YUM下载安装PostgreSQL1.下载PostgreSQL安装包2.安装PostgreS…...

PHP的垃圾回收机制是怎样的?
PHP 使用自动垃圾回收机制来管理内存。PHP 的垃圾回收主要依赖于引用计数和周期性垃圾回收两种策略。 引用计数: PHP 使用引用计数来跟踪变量的引用次数。每当一个变量被引用,其引用计数就增加;每当一个引用被释放,计数就减少。当…...

【数据结构】八大排序之希尔排序算法
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 一.优化直接插入排序算法 我们在之前对直接插入排序算法的优化部分通过对直接插入排序的分析可以得到一个结论,即: 进行直接插入排序的数组,如果越接近局部有序,则后续进行直…...

NestJS使用gRPC实现微服务通信
代码仓库地址:https://github.com/zeng-jc/rpc-grpc-practice 1.1 基本概念 gRPC 基于 Protocol Buffers(protobuf)作为接口定义语言(IDL),意味着你可以使用 protobuf 来定义你的服务接口,gRP…...

Android手机使用Termux终端模拟器
Termux 是 Android 平台上的一个终端模拟器,可以在 Android 手机上模拟 Linux 环境。它提供命令行界面,并且提供了功能健全的包管理工具(pkg)。另外就是 Termux 不需要 root 权限,安装后默认产生一个用户,可…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
