嵌入式培训-数据结构-day23-线性表
线性表
线性表是包含若干数据元素的一个线性序列 记为: L=(a0, ...... ai-1, ai, ai+1 ...... an-1)
L为表名,ai (0≤i≤n-1)为数据元素;
n为表长,n>0 时,线性表L为非空表,否则为空表。
线性表L可用二元组形式描述(任何一种数据结构都能表示为二元组):
L= (D,R)
data、relation
即线性表L包含数据元素集合D和关系集合R
D={ai | ai∈datatype ,i=0,1,2, ∙∙∙∙∙∙∙∙∙n-1 ,n≥0}
R={<ai , ai+1> | ai , ai+1∈D, 0≤i≤n-2}
关系符<ai, ai+1>在这里称为有序对
表示任意相邻的两个元素之间的一种先后次序关系
ai是ai+1的直接前驱, ai+1是ai的直接后继
设有一个顺序表L={1,2,3,4,5,6}; 他们的关系如图:

使用二元组描述L=(D,R),则
D={1 , 2 , 3 , 4 , 5 , 6}(n=6)
R={<1,2> , <2,3> , <3,4> , <4,5> , <5,6>}
线性表的特征:
1) 对非空表,a0是表头,无前驱;
2) an-1是表尾,无后继;
3) 其它的每个元素ai有且仅有一个直接前驱ai-1和一个直接后继ai+1。
顺序存储结构的表示
若将线性表L=(a0,a1, ……,an-1)中的各元素依次存储于计算机一片连续的存储空间。
设Loc(ai)为ai的地址,Loc(a0)=b,每个元素占d个单元 则:Loc(ai)=b+i*d

顺序存储结构的特点
逻辑上相邻的元素 ai, ai+1,其存储位置也是相邻的
对数据元素ai的存取为随机存取或按地址存取
存储密度高
存储密度D=(数据结构中元素所占存储空间)/(整个数据结构所占空间)
顺序存储结构的不足:
对表的插入和删除等运算的时间复杂度较差。
所以对于查找较多、插入删除较少的实际问题,可以用顺序存储。
对于顺序存储编程,一般需要至少两个结构体,一个存数据元素的各种信息,一个存数据元素的集合。
一般至少要有sqlist.h(定义,运算)、sqlist.c(运算的实现)、test.c(主函数)。这种程序结构就叫架构,写程序前先想好架构。
在C语言中,可借助于一维数组类型来描述线性表的顺序存储结构
#define N 100
typedef int data_t;
typedef struct
{ data_t data[N]; //表的存储空间
int last;
} sqlist, *sqlink;

线性表的基本运算
设线性表 L=(a0,a1, ……,an-1),对 L的基本运算有:
1)建立一个空表:list_create(L)
2)置空表:list_clear(L)
3)判断表是否为空:list_empty (L)。若表为空,返回值为1 , 否则返回 0
4)求表长:length (L)
5)取表中某个元素:GetList(L , i ), 即ai。要求0≤i≤length(L)-1
6)定位运算:Locate(L,x)。确定元素x在表L中的位置(或序号)
Locate(L,x)= i 当元素x=ai∈L,且ai是第一个与x相等时;
-1 x不属于L时。
基本运算的相关算法
定位:确定给定元素x在表L中第一次出现的位置(或序号)。即实现Locate(L,x)。算法对应的存储结构如图所示。

7)插入:
Insert(L,x,i)。将元素x插入到表L中第i个元素ai之前,且表长+1。
插入前: (a0,a1,---,ai-1,ai,ai+1-------,an-1) 0≤i≤n,i=n时,x插入表尾
插入后: (a0,a1,---,ai-1, x, ai,ai+1-------,an-1)
基本运算的相关算法
算法思路:若表存在空闲空间,且参数i满足:0≤i≤L->last+1,则可进行正常插入。插入前,将表中(L->data[L->last]~L->data[i])部分顺序下移一个位置,然后将x插入L->data[i]处即可。算法对应的表结构。

8)删除:
Delete(L,i)。删除表L中第i个元素ai,且表长减1, 要求0≤i≤n-1。
删除前: (a0,a1,---,ai-1,ai,ai+1-------,an-1)
删除后: (a0,a1,---,ai-1,ai+1-------,an)
删除:将表中第i个元素ai从表中删除,即实现DeleteSqlist(L, i)。 算法思路: 若参数i满足:0≤i≤L->last, 将表中L->data[i+1]∽L->data[L->last] 部分顺序向上移动一个位置,覆盖L->data[i]。

线性表的基本运算
设线性表La=(a0a1, ……,am-1), Lb= (b0b1, ……,bn-1),求La∪Lb =>La,

算法思路:依次取表Lb中的bi(i=0,1,……,n-1),若bi不属于La,则将其插入表La中。
线性表
设计清除线性表L=(a0,a1,---,ai,-------,an-1)中重复元素的算法。
算法思路:对当前表L中的每个ai(0≤i≤n-2),依次与aj(i+1≤j≤n-1)
比较,若与ai相等,则删除之。
线性表的顺序存储缺点
线性表的顺序存储结构有存储密度高及能够随机存取等优点,但存在以下不足:
(1)要求系统提供一片较大的连续存储空间。
(2)插入、删除等运算耗时,且存在元素在存储器中成片移动的现象;
vi编辑器底行模式下,:vsp 文件名,可以让打开的文件和这个文件分屏显示。
相关文章:

嵌入式培训-数据结构-day23-线性表
线性表 线性表是包含若干数据元素的一个线性序列 记为: L(a0, ...... ai-1, ai, ai1 ...... an-1) L为表名,ai (0≤i≤n-1)为数据元素; n为表长,n>0 时,线性表L为非空表,否则为空表。 线性表L可用二元组形式描述…...
C# DotNetCore AOP简单实现
背景 实际开发中业务和日志尽量不要相互干扰嵌套,否则很难维护和调试。 示例 using System.Reflection;namespace CSharpLearn {internal class Program{static void Main(){int age 25;string name "bingling";Person person new(age, name);Conso…...

19.Tomcat搭建
Tomcat 简介 Tomcat的安装和启动 前置条件 • JDK 已安装(JAVA_HOME环境变量已被成功配置) Windows 下安装 访问 http://tomcat.apache.org ⇒ 左侧边栏 “Download” 2. 解压缩下载的文件到 “D:\tomcat”, tomcat的内容最终被解压到 “D:\tomcat\apache-tomcat-9.0.84” 3.…...

HarmonyOS云开发基础认证考试满分答案(100分)【全网最全-不断更新】【鸿蒙专栏-29】
系列文章: HarmonyOS应用开发者基础认证满分答案(100分) HarmonyOS应用开发者基础认证【闯关习题 满分答案】 HarmonyOS应用开发者高级认证满分答案(100分) HarmonyOS云开发基础认证满分答案(100分…...

Unity项目里Log系统该怎么设计
其实并没有想完整就设计一个好用的Log系统,然后发出来。记录这个的原因,是在书里看到这么一句话,Log会消耗资源,特别是写文件,因此可以设置一个Log缓冲区,等缓冲区满了再一次性写入文件,以节省资…...

设计模式-状态(State)模式
目录 开发过程中的一些场景 状态模式的简单介绍 状态模式UML类图 类图讲解 适用场景 Java中的例子 案例讲解 什么是状态机 如何实现状态机 SpringBoot状态自动机 优点 缺点 与其他模式的区别 小结 开发过程中的一些场景 我们在平时的开发过程中,经常会…...

oracle怎么存放json好
Oracle数据库提供了多种方式来存储JSON数据。你可以将JSON数据存储在VARCHAR2、CLOB或BLOB数据类型中,或者使用Oracle提供的JSON数据类型。 如果你选择使用VARCHAR2数据类型来存储JSON数据,你可以直接将JSON字符串存储在其中。例如: CREATE…...

【计算机网络】—— 详解码元,传输速率的计算|网络奇缘系列|计算机网络
🌈个人主页: Aileen_0v0🔥系列专栏: 一见倾心,再见倾城 --- 计算机网络~💫个人格言:"没有罗马,那就自己创造罗马~" 目录 码元 速率和波特 思考1 思考2 思考3 带宽(Bandwidth) 📝总结 码元…...
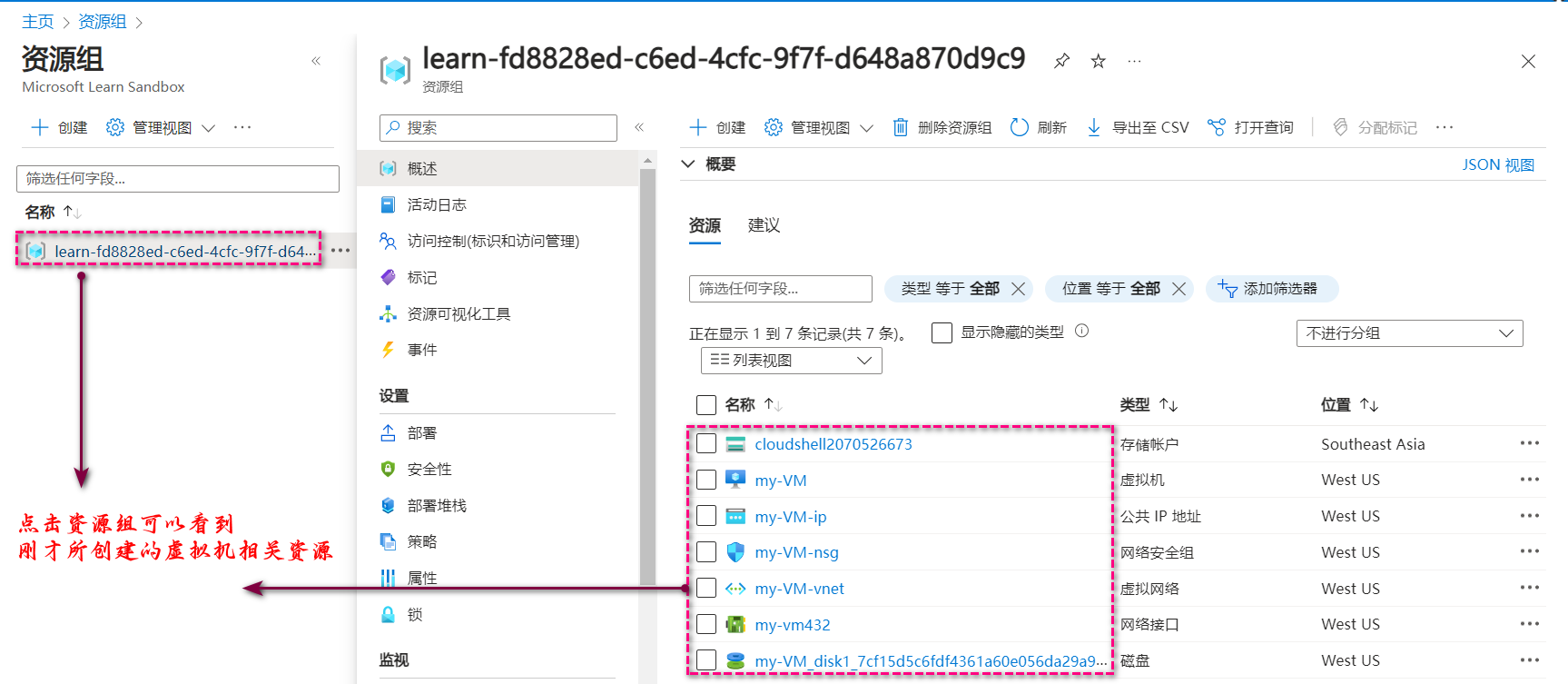
[ 云计算 | Azure 实践 ] 在 Azure 门户中创建 VM 虚拟机并进行验证
文章目录 一、前言二、在 Azure Portal 中创建 VM三、验证已创建的虚拟机资源3.1 方法一:在虚拟机服务中查看验证3.1 方法二:在资源组服务中查看验证 四、文末总结 一、前言 本文会开始创建新系列的专栏,专门更新 Azure 云实践相关的文章。 …...
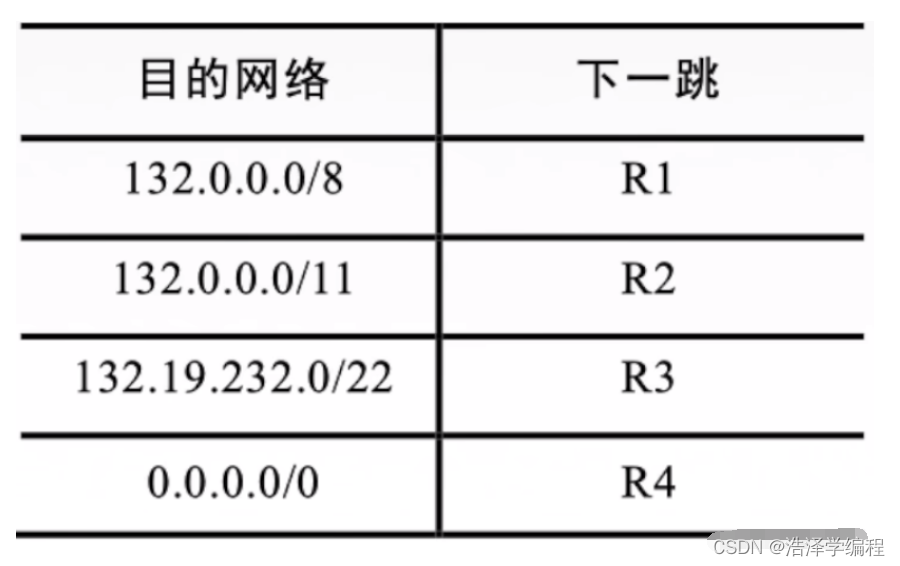
计算机网络:网络层(无分类编址CIDR、计算题讲解)
带你快速通关期末 文章目录 前言一、无分类编址CIDR简介二、构成超网三、最长前缀匹配总结 前言 我们在前面知道了分类地址,但是分类地址又有很多缺陷: B类地址很快将分配完毕!路由表中的项目急剧增长! 一、无分类编址CIDR简介 无分类域间路由选择CI…...

Learning Semantic-Aware Knowledge Guidance forLow-Light Image Enhancement
微光图像增强(LLIE)研究如何提高照明并生成正常光图像。现有的大多数方法都是通过全局和统一的方式来改善低光图像,而不考虑不同区域的语义信息。如果没有语义先验,网络可能很容易偏离区域的原始颜色。为了解决这个问题࿰…...

关于嵌入式开发的一些信息汇总:开发模型以及自托管开发(二)
关于嵌入式开发的一些信息汇总:开发模型及自托管开发(二) 2 自托管开发2.2 构建 Raspberry Pi 内核2.3 安装内核2.4 总结 3 连接目标板3.1 Raspberry Pi 上的网络设置3.2 Ssh、rsh、rlogin 和 telnet 连接到目标 4 应用程序开发4.1 在目标板上…...

【JavaEE】多线程案例 - 定时器
作者主页:paper jie_博客 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文于《JavaEE》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精力)打造&…...
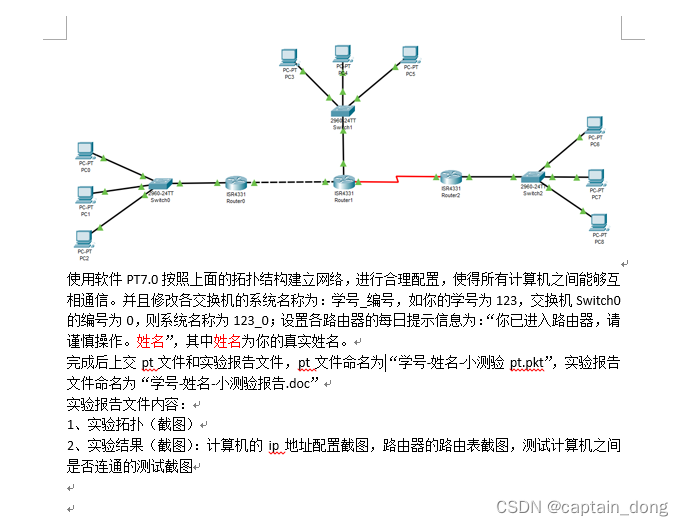
网络小测------
使用软件PT7.0按照上面的拓扑结构建立网络,进行合理配置,使得所有计算机之间能够互相通信。并且修改各交换机的系统名称为:学号_编号,如你的学号为123,交换机Switch0的编号为0,则系统名称为123_0࿱…...

基于linux系统的Tomcat+Mysql+Jdk环境搭建(二)jdk1.8 linux 上传到MobaXterm 工具的已有session里
【JDK安装】 1.首先下载一个JDK版本 官网地址:http://www.oracle.com/technetwork/java/javase/downloads/jdk8-downloads-2133151.html 下载1.8版本,用红框标注出来了: 也许有的同学看到没有1.8版本,你可以随便下载一个linux的…...

04-Nacos中负载均衡规则的配置
负载均衡规则 同集群优先 默认的ZoneAvoidanceRule实现并不能根据同集群优先的规则来实现负载均衡,Nacos中提供了一个实现叫NacosRule可以优先从同集群中挑选服务实例 当服务消费者在本地集群找不到服务提供者时也会去其他集群中寻找,但此时会在服务消费者的控制台报警告 第…...
 ?))
Kotlin 中的 `use` 关键字:优化资源管理(避免忘记inputStream.close() ?)
在 Android开发中,正确且高效地管理资源是至关重要的。use 关键字在 Kotlin 中为资源管理提供了一个简洁且强大的解决方案。它主要用于自动管理那些需要关闭的资源,比如文件、网络连接等。 一、use 关键字的工作原理 🤖 use 是一个扩展函数…...
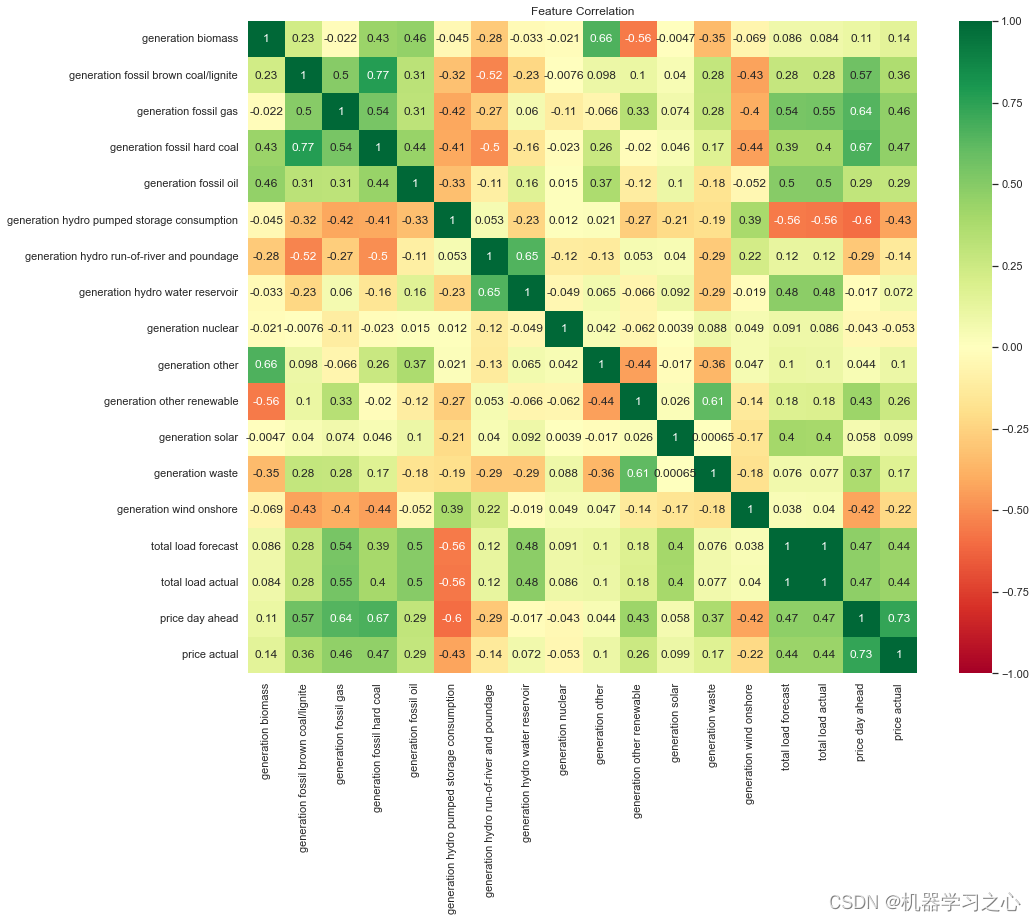
时序预测 | Python实现GRU-XGBoost组合模型电力需求预测
时序预测 | Python实现GRU-XGBoost组合模型电力需求预测 目录 时序预测 | Python实现GRU-XGBoost组合模型电力需求预测预测效果基本描述程序设计参考资料预测效果 基本描述 该数据集因其每小时的用电量数据以及 TSO 对消耗和定价的相应预测而值得注意,从而可以将预期预测与当前…...
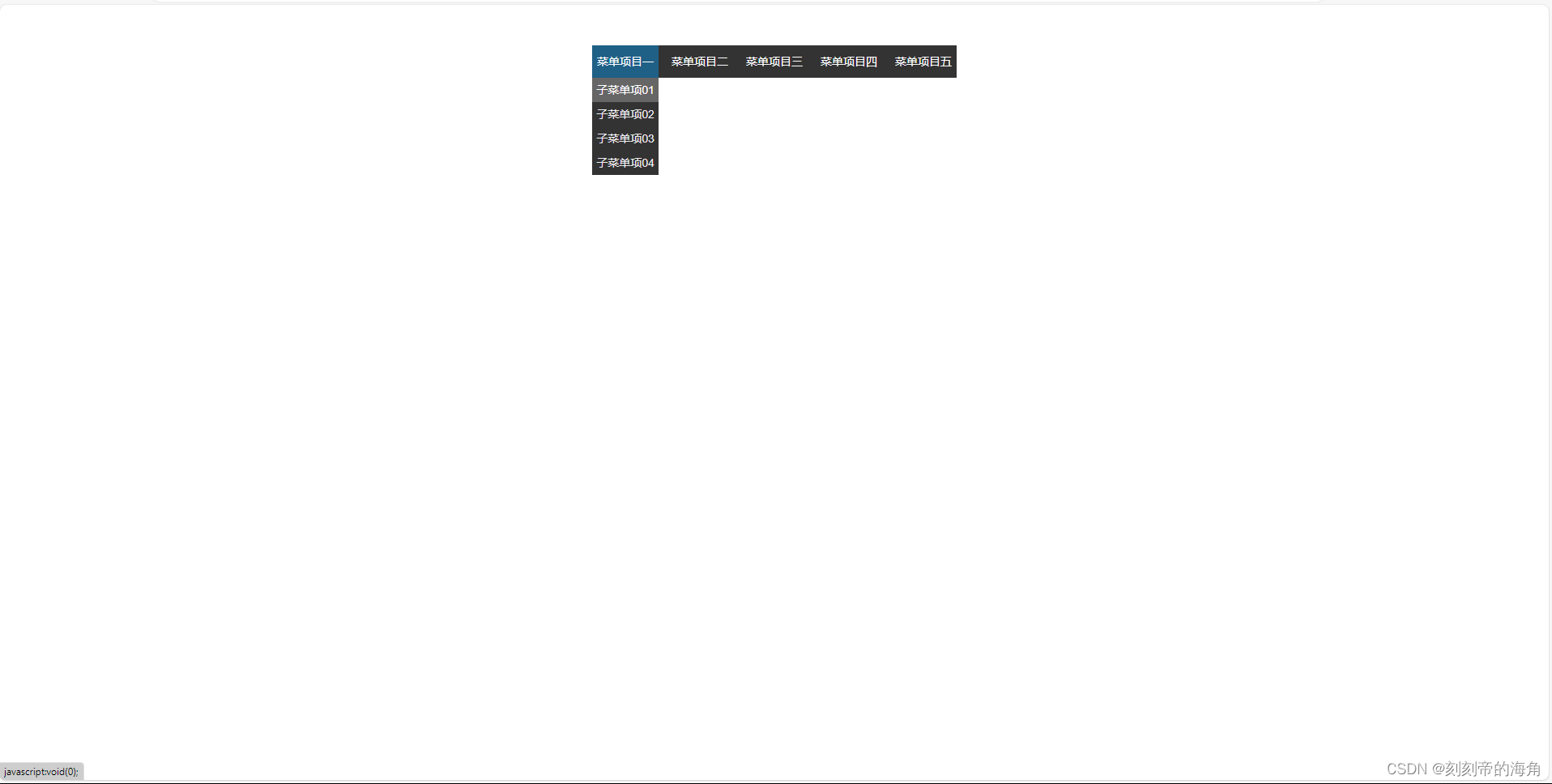
扁平化菜单功能制作
网页效果: HTML部分: <body><ul class"nav"><li><a href"javascript:void(0);">菜单项目一</a><ul><li>子菜单项01</li><li>子菜单项02</li><li>子菜单项03<…...
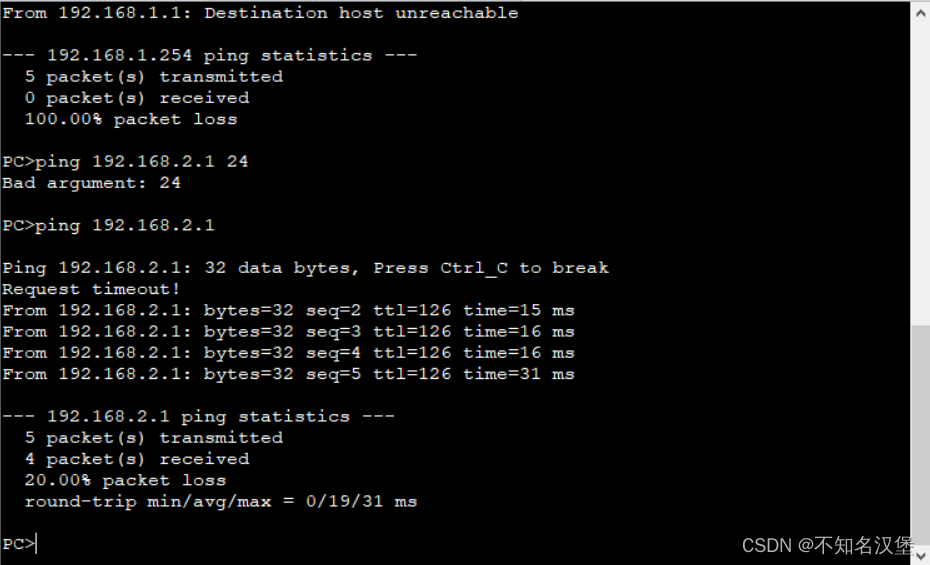
网络基础——路由协议及ensp操作
目录 一、路由器及路由表 1.路由协议: 2.路由器转发原理: 3.路由表: 二、静态路由优缺点及特殊静态路由默认路由 1.静态路由的优缺点: 2.下一跳地址 3.默认路由 三、静态路由配置 四、补充备胎 平均负载 五、补充&…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...
