当前位置： 首页 > news >正文

SVN忽略文件的两种方式

news 2026/2/11 1:44:20

当使用版本管理工具时，提交到代码库的文档我们不希望存在把一些临时文件也推送到仓库中，这样就需要用到忽略文件。SVN的忽略相比于GIT稍显麻烦，GIT只需要在.gitignore添加忽略规则即可。而SVN有两种忽略方式，一个是全局设置，另一个是针对版本库设置。

1.SVN全局忽略

步骤 ：右键 -> tortoiseSVN -> Settings -> General -> Global ignore pattern -> 添加自己需要忽略的文件。

这种方式忽略有一个缺点，当我们的SVN客户端重装了，或者我们换电脑了，这个忽略方式就失效了，这是SVN软件的配置，而不是版本库的配置。同时这样操作也不能满足每一个仓库的个性化需求。

2.SVN仓库设置

为了克服SVN全局忽略的弊端，如果希望每一个仓库有不同的设置，那么需要如下操作步骤：

右键 -> tortoiseSVN -> Properties -> New… -> Other -> Property name -> svn:ignore 然后再Property value中添加需要忽略的文件名或规则。

一般情况下希望每一个目录都执行这个规则，可以选中Aplly property recursively设置成递归的方式，这样每一个目录都会应用这个规则。

相关文章：

SVN忽略文件的两种方式

当使用版本管理工具时，提交到代码库的文档我们不希望存在把一些临时文件也推送到仓库中，这样就需要用到忽略文件。SVN的忽略相比于GIT稍显麻烦，GIT只需要在.gitignore添加忽略规则即可。而SVN有两种忽略方式，一个是全局设置&#…...

编程日记 2023/12/18 3:01:32

手写VUE后台管理系统10 - 封装Axios实现异常统一处理

目录 前后端交互约定安装创建Axios实例拦截器封装请求方法业务异常处理 axios 是一个易用、简洁且高效的http库 axios 中文文档：http://www.axios-js.com/zh-cn/docs/ 前后端交互约定 在本项目中，前后端交互统一使用 application/json;charsetUTF-8 的请…...

编程日记 2023/12/18 3:00:31

JavaScript装饰者模式

JavaScript装饰者模式 1 什么是装饰者模式2 模拟装饰者模式3 JavaScript的装饰者4 装饰函数5 AOP装饰函数6 示例：数据统计上报 1 什么是装饰者模式 在程序开发中，许多时候都我们并不希望某个类天生就非常庞大，一次性包含许多职责。那么我们就…...

编程日记 2023/12/18 2:58:28

C++学习笔记01

01.C概述&#xff08;了解&#xff09; c语言在c语言的基础上添加了面向对象编程和泛型编程的支持。 02.第一个程序helloworld&#xff08;掌握&#xff09; #define _CRT_SECURE_NO_WARNINGS #include<iostream> using namespace std;//标准命名空间int main() {//co…...

编程日记 2023/12/18 2:55:26

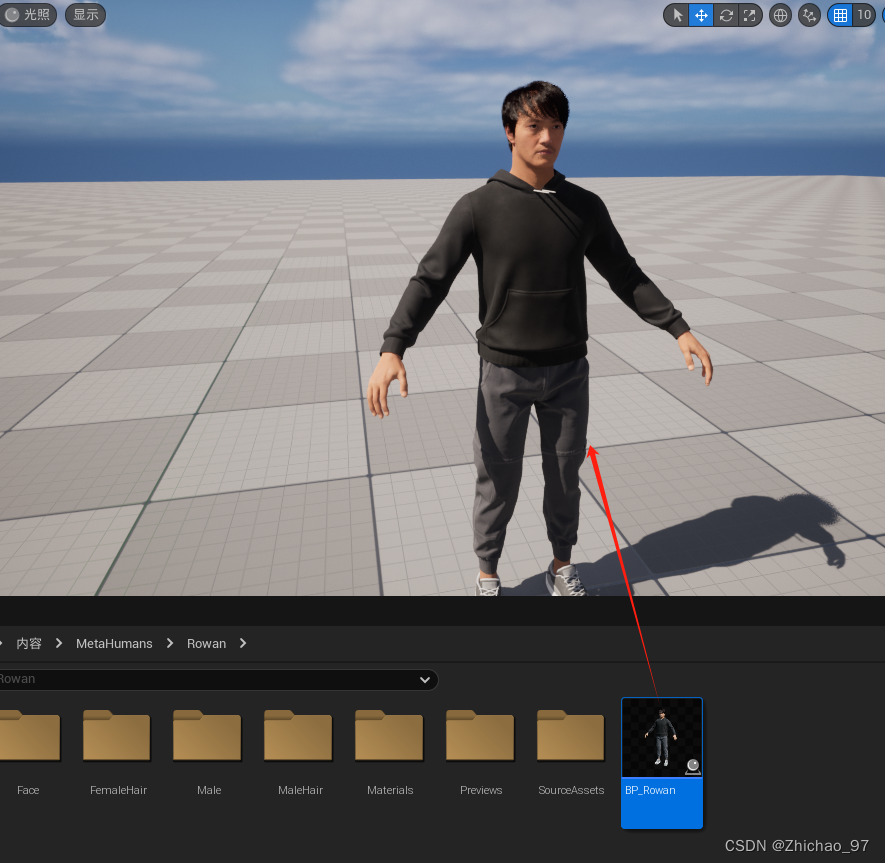
【UE5】初识MetaHuman 创建虚拟角色

步骤 在UE5工程中启用“Quixel Bridge”插件 打开“Quixel Bridge” 点击“MetaHumans-》MetaHuman Presets UE5” 点击“START MHC” 在弹出的网页中选择一个虚幻引擎版本&#xff0c;然后点击“启动 MetaHuman Creator” 等待一段时间后&#xff0c;在如下页面点击选择一个人…...

编程日记 2023/12/18 2:54:25

物流实时数仓：数仓搭建（DWD）一

系列文章目录 物流实时数仓&#xff1a;采集通道搭建 物流实时数仓&#xff1a;数仓搭建 物流实时数仓&#xff1a;数仓搭建&#xff08;DIM&#xff09; 物流实时数仓&#xff1a;数仓搭建&#xff08;DWD&#xff09;一 文章目录 系列文章目录前言一、文件编写1.目录创建2.b…...

编程日记 2023/12/18 2:52:23

MATLAB安装

亲自验证有效&#xff0c;多谢这位网友的分享&#xff1a; https://blog.csdn.net/xiajinbiaolove/article/details/88907232...

编程日记 2023/12/18 2:50:21

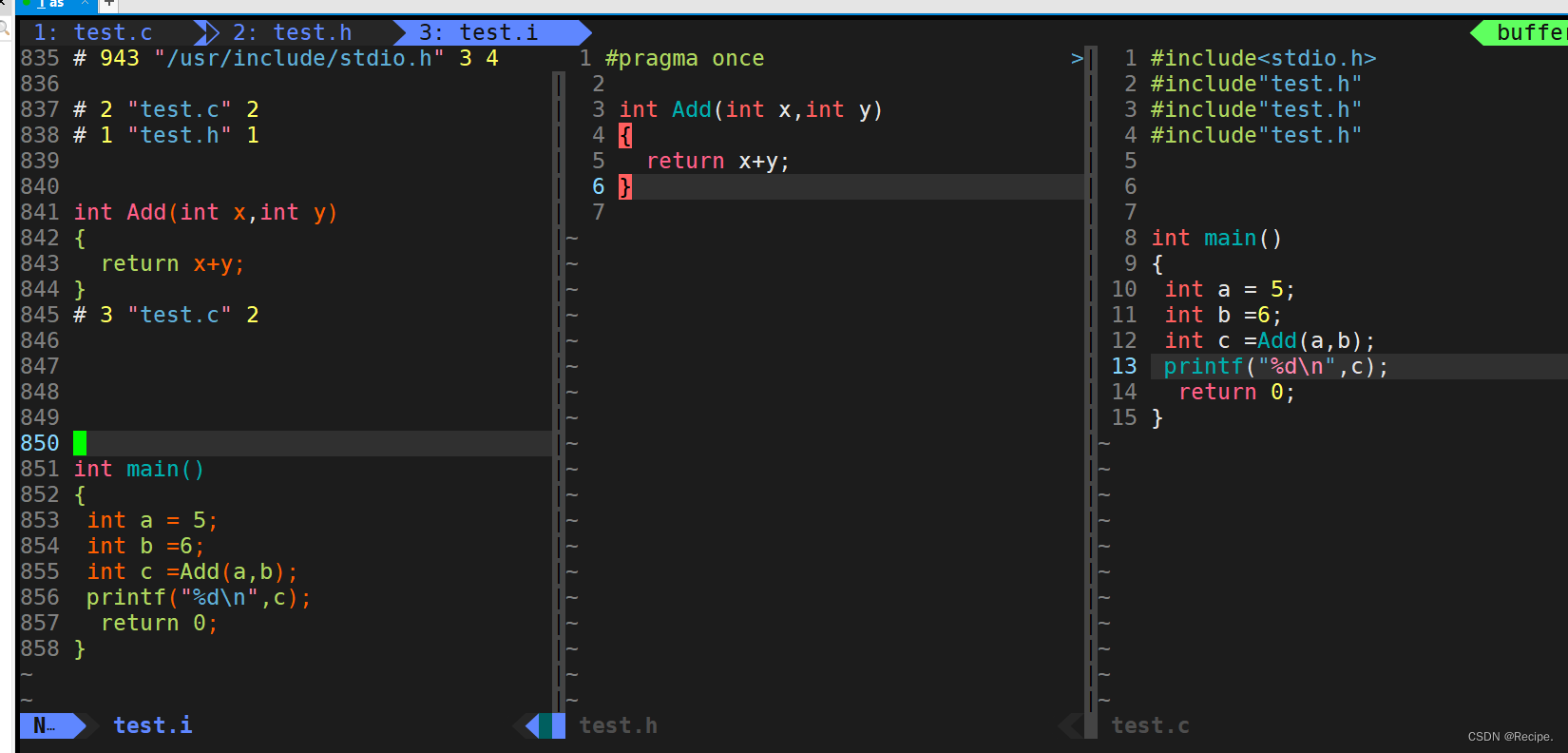
C语言——预处理详解(#define用法+注意事项）

#define 语法规定 #define定义标识符 语法: #define name stuff #define例子 #include<stdio.h> #define A 100 #define STR "abc" #define FOR for(;;)int main() {printf("%d\n", A);printf("%s\n", STR);FOR;return 0; } 运行结果…...

编程日记 2023/12/18 2:45:17

Linux（23）：Linux 核心编译与管理

编译前的任务&#xff1a;认识核心与取得核心原始码 Linux 其实指的是核心。这个【核心(kernel)】是整个操作系统的最底层&#xff0c;他负责了整个硬件的驱动&#xff0c;以及提供各种系统所需的核心功能&#xff0c;包括防火墙机制、是否支持 LVM 或 Quota 等文件系统等等&a…...

编程日记 2023/12/18 2:44:15

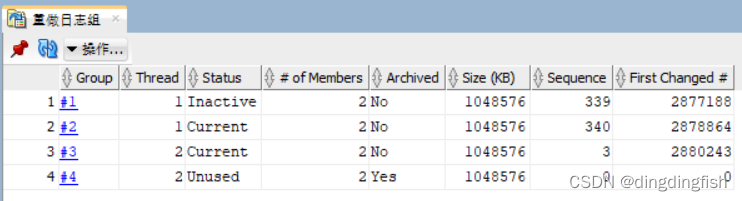
Oracle RAC环境下redo log 文件的扩容

环境&#xff1a; 有一个2节点RAC每一个节点2个logfile group每一个group含2个member每一个member的大小为200M 目标&#xff1a;将每一个member的大小有200M扩充到1G。 先来看下redo log的配置&#xff1a; SQL> select * from v$log;GROUP# THREAD# SEQUENCE# …...

编程日记 2023/12/18 2:41:12

Java入门学习笔记一

一、Java语言环境搭建 1、JAVA语言的跨平台原理 1.1、什么是跨平台性&#xff1f; 跨平台就是说&#xff0c;同一个软件可以在不同的操作系统&#xff08;例如&#xff1a;Windows、Linux、mad&#xff09;上执行&#xff0c;而不需要对软件做任务处理。即通过Java语言编写的…...

编程日记 2023/12/18 2:38:10

分布式块存储 ZBS 的自主研发之旅｜元数据管理

重点内容 元数据管理十分重要&#xff0c;犹如整个存储系统的“大黄页”&#xff0c;如果元数据操作出现性能瓶颈&#xff0c;将严重影响存储系统的整体性能。如何提升元数据处理速度与高可用是元数据管理的挑战之一。SmartX 分布式存储 ZBS 采用 Log Replication 的机制&…...

编程日记 2023/12/18 2:36:07

六大设计原则

六大设计原则 1、单一职责原则 一个类或者模块只负责完成一个职责或者功能。 2、开放封闭原则 规定软件中的对象、类、模块和函数对扩展应该是开放的&#xff0c;对于修改应该是封闭的。用抽象定义结构&#xff0c;用具体实现扩展细节。 3、里氏替换原则 如果S是T的子类型…...

编程日记 2023/12/18 2:33:05

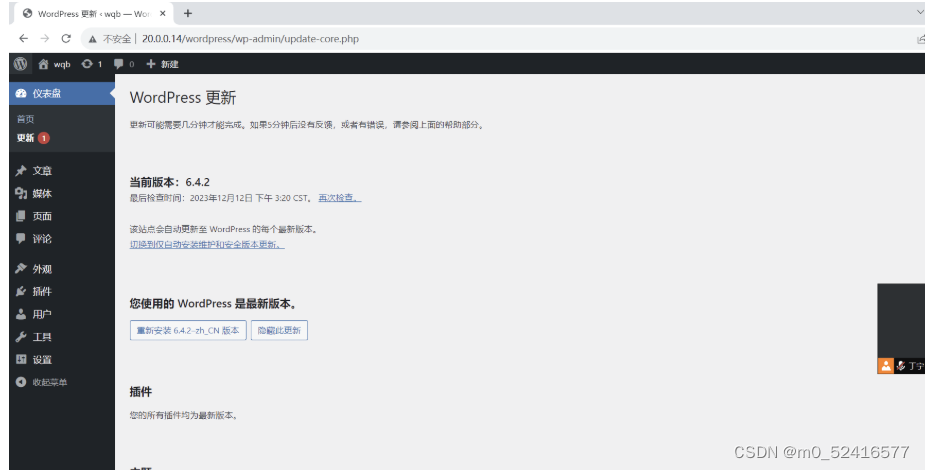
dockerfile创建镜像 lNMP+wordpress

dockerfile创建镜像 lNMPwordpress nginx dockernginx mysql dockermysql php dockerphp nginx vim nginx.conf vim Dockerfile docker network create --subnet172.17.0.0/16 --opt "com.docker.network.bridge.name""docker1" mynetwork docker buil…...

编程日记 2023/12/18 2:29:02

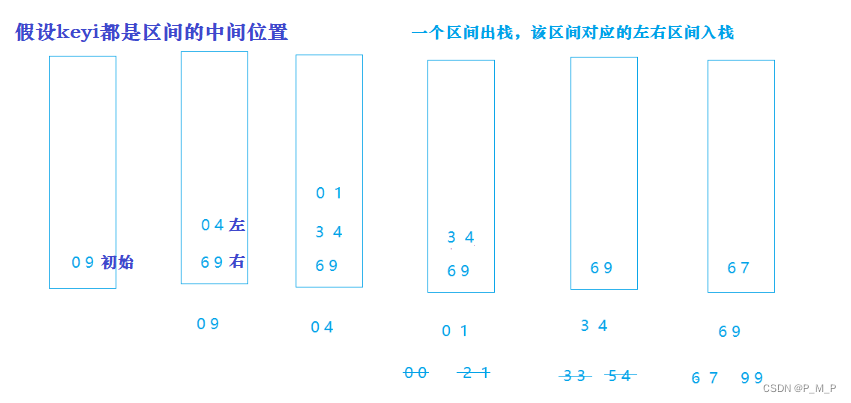
深入理解——快速排序

目录 &#x1f4a1;基本思想 &#x1f4a1;基本框架 &#x1f4a1;分割方法 ⭐Hoare版本 ⭐挖坑法 ⭐前后指针法 &#x1f4a1;优化方法 ⭐三数取中法 ⭐小区间内使用插入排序 &#x1f4a1;非递归实现快速排序 &#x1f4a1;性能分析 &#x1f4a1;基本思想 任取待排…...

编程日记 2023/12/18 2:27:00

【代码随想录】算法训练计划50

dp 1、123. 买卖股票的最佳时机 III 题目&#xff1a; 给定一个数组&#xff0c;它的第 i 个元素是一支给定的股票在第 i 天的价格。 设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。 注意&#xff1a;你不能同时参与多笔交易&#xff08;你必须在再次购…...

编程日记 2023/12/18 2:21:56

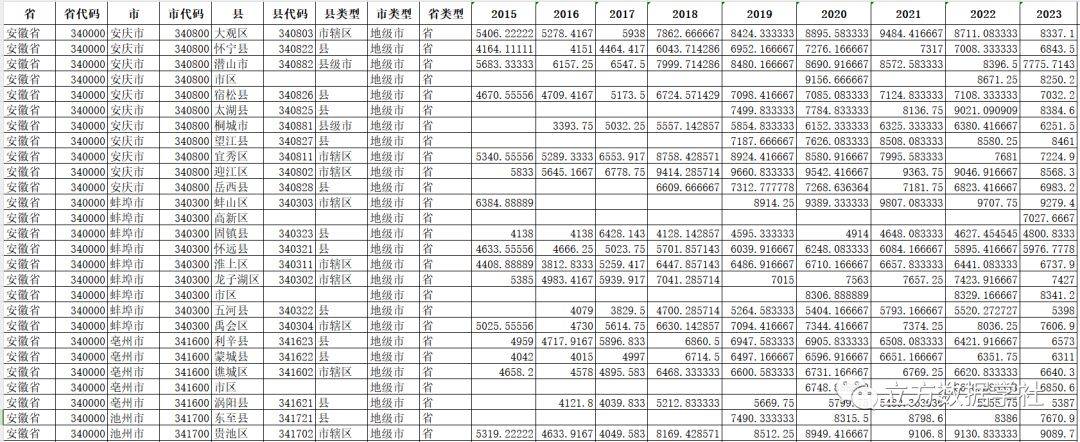
【数据分享】2019-2023年我国区县逐年二手房房价数据（Excel/Shp格式）

房价是一个区域发展程度的重要体现&#xff0c;一个区域的房价越高通常代表这个区域越发达&#xff0c;对于人口的吸引力越大&#xff01;因此&#xff0c;房价数据是我们在各项城市研究中都非常常用的数据&#xff01;之前我们分享了2019—2023年我国区县逐月的二手房房价数据…...

编程日记 2023/12/18 2:19:54

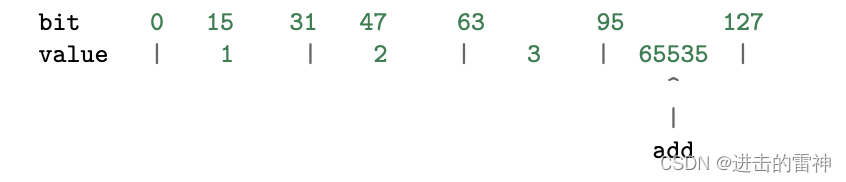
Redis设计与实现之整数集合

目录 一、内存映射数据结构 二、整数集合 1、整数集合的应用 2、数据结构和主要操作 3、intset运行实例 创建新intset 添加新元素到 intset 添加新元素到 intset&#xff08;不需要升级&#xff09; 添加新元素到 intset (需要升级) 4、升级 升级实例 5、关于升级 …...

编程日记 2023/12/18 2:14:49

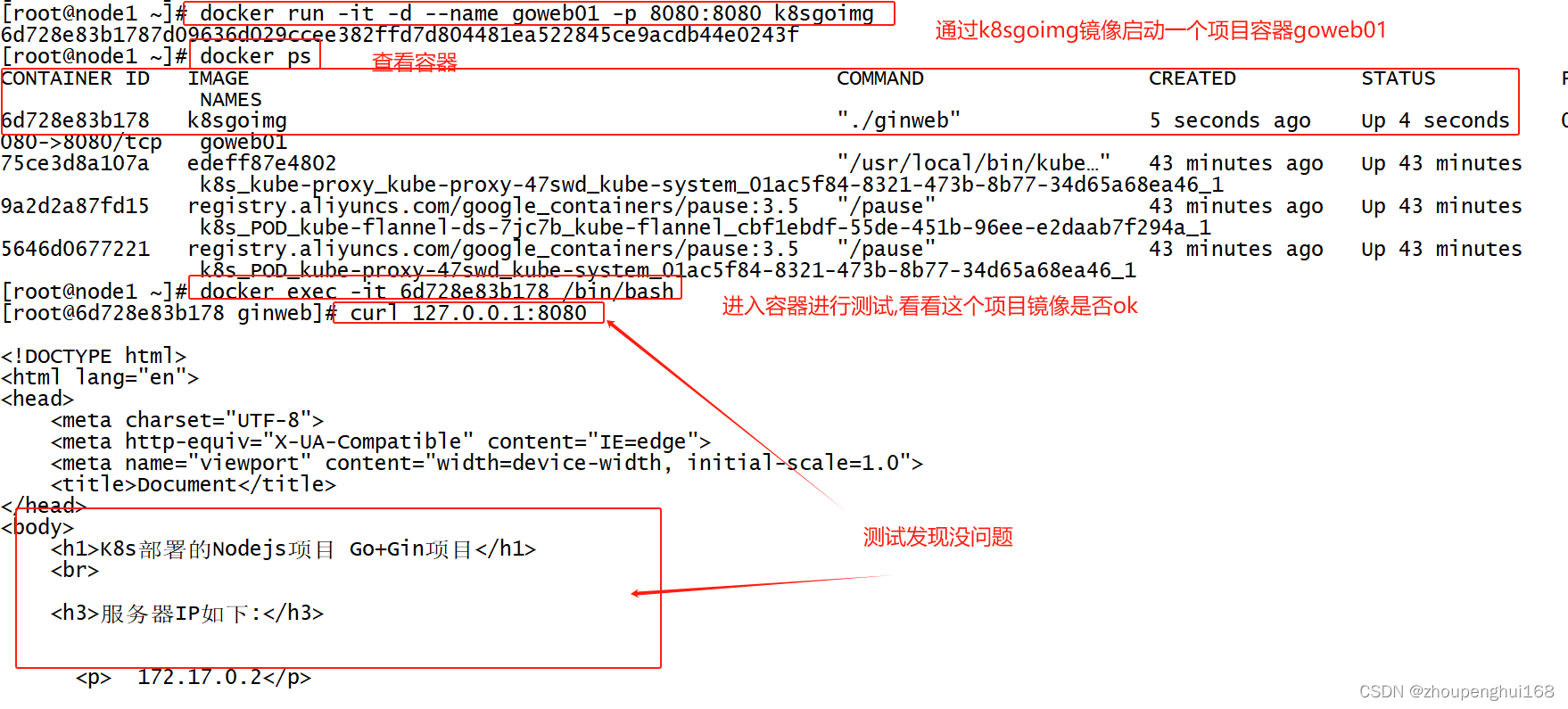
[Kubernetes]2. k8s集群中部署基于nodejs golang的项目以及Pod、Deployment详解

一. 创建k8s部署的镜像 1.部署nodejs项目 (1).上传nodejs项目到节点node1 (2).压缩nodejs项目 (3).构建nodejsDockerfile 1).创建nodejsDockerfile 具体可参考:[Docker]十.Docker Swarm讲解,在/root下创建nodejsDockerfile,具体代码如下: FROM node #把压缩文件COPY到镜像的…...

编程日记 2023/12/18 2:12:47

讯飞星火大模型api调用

讯飞星火大模型&#xff0c;通过websocket方式通信传递协议要求的报文&#xff0c;然后将流式返回的报文拼接为完整的响应内容&#xff0c;status2时是最后一条消息。因为是websocket方式所以是异步响应的&#xff0c;如果想要同步需要使用CountDownLatch控制下线程等待最后一条…...

编程日记 2023/12/18 2:11:46

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】

微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来&#xff0c;Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

编程新知 2026/2/1 19:08:45

Qt Http Server模块功能及架构

Qt Http Server 是 Qt 6.0 中引入的一个新模块&#xff0c;它提供了一个轻量级的 HTTP 服务器实现&#xff0c;主要用于构建基于 HTTP 的应用程序和服务。 功能介绍&#xff1a; 主要功能 HTTP服务器功能&#xff1a; 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

编程新知 2025/10/17 21:16:57

linux 下常用变更-8

1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行&#xff0c;YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID&#xff1a; YW3…...

编程新知 2025/10/7 15:08:22

dify打造数据可视化图表

一、概述 在日常工作和学习中&#xff0c;我们经常需要和数据打交道。无论是分析报告、项目展示&#xff0c;还是简单的数据洞察&#xff0c;一个清晰直观的图表&#xff0c;往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server&#xff0c;由蚂蚁集团 AntV 团队…...

编程新知 2026/1/20 20:10:03

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数 在软件开发中，单例模式（Singleton Pattern）是一种常见的设计模式，确保一个类仅有一个实例，并提供一个全局访问点。在多线程环境下，实现单例模式时需要注意线程安全问题，以防止多个线程同时创建实例，导致…...

编程新知 2025/11/25 19:50:27

Python Ovito统计金刚石结构数量

大家好，我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构，但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法，可以持续统计各步的金刚石结构，具体代码如下： from ovito…...

编程新知 2026/1/26 5:39:08

站群服务器的应用场景都有哪些？

站群服务器主要是为了多个网站的托管和管理所设计的&#xff0c;可以通过集中管理和高效资源的分配&#xff0c;来支持多个独立的网站同时运行&#xff0c;让每一个网站都可以分配到独立的IP地址&#xff0c;避免出现IP关联的风险&#xff0c;用户还可以通过控制面板进行管理功…...

编程新知 2025/9/1 19:01:24

从面试角度回答Android中ContentProvider启动原理

Android中ContentProvider原理的面试角度解析&#xff0c;分为​​已启动​​和​​未启动​​两种场景&#xff1a; 一、ContentProvider已启动的情况 1. ​​核心流程​​ ​​触发条件​​&#xff1a;当其他组件&#xff08;如Activity、Service&#xff09;通过ContentR…...

编程新知 2025/10/2 19:46:59

五子棋测试用例

一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏&#xff0c;有着深厚的文化底蕴。通过将五子棋制作成网页游戏&#xff0c;可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家&#xff0c;都可以通过网页五子棋感受到东方棋类…...

编程新知 2026/2/1 21:56:50

实战设计模式之模板方法模式

概述 模板方法模式定义了一个操作中的算法骨架&#xff0c;并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下&#xff0c;重新定义算法中的某些步骤。简单来说&#xff0c;就是在一个方法中定义了要执行的步骤顺序或算法框架&#xff0c;但允许子类…...

编程新知 2026/2/9 21:59:15