深入理解——快速排序
目录
💡基本思想
💡基本框架
💡分割方法
⭐Hoare版本
⭐挖坑法
⭐前后指针法
💡优化方法
⭐三数取中法
⭐小区间内使用插入排序
💡非递归实现快速排序
💡性能分析
💡基本思想
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
💡基本框架
// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int* array, int left, int right)
{if(right - left <= 1)return;// 按照基准值对array数组的 [left, right)区间中的元素进行划分int div = partion(array, left, right);// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)// 递归排[left, div)QuickSort(array, left, div);// 递归排[div+1, right)QuickSort(array, div+1, right);
}这是快速排序递归实现的主框架,可以发现与二叉树的递归十分相似,在递归时可以想想二叉树的递归规则。
💡分割方法
⭐Hoare版本
这是Hoare于1962年提出的一种二叉树结构的交换排序方法
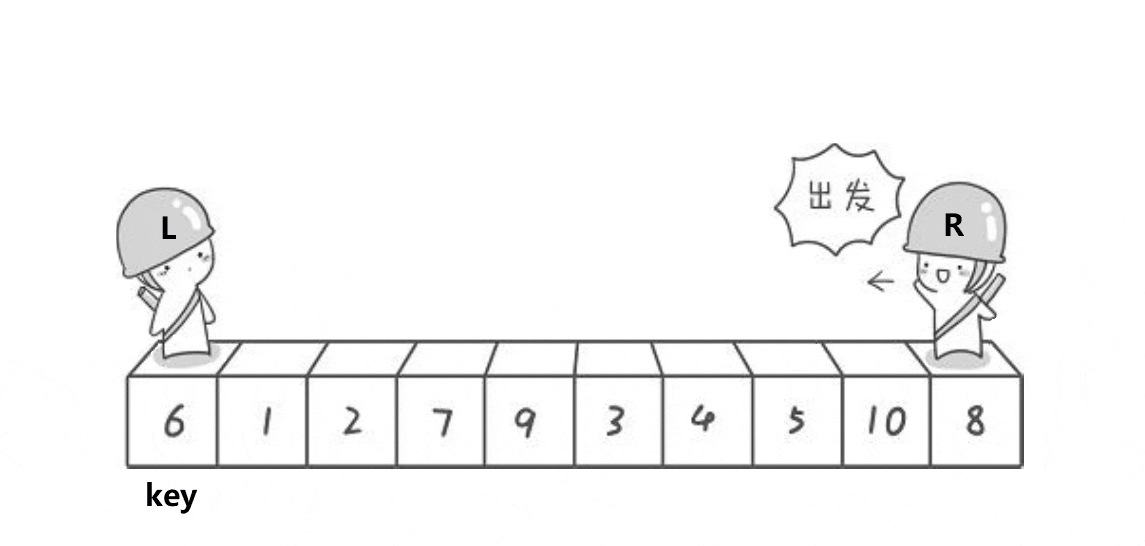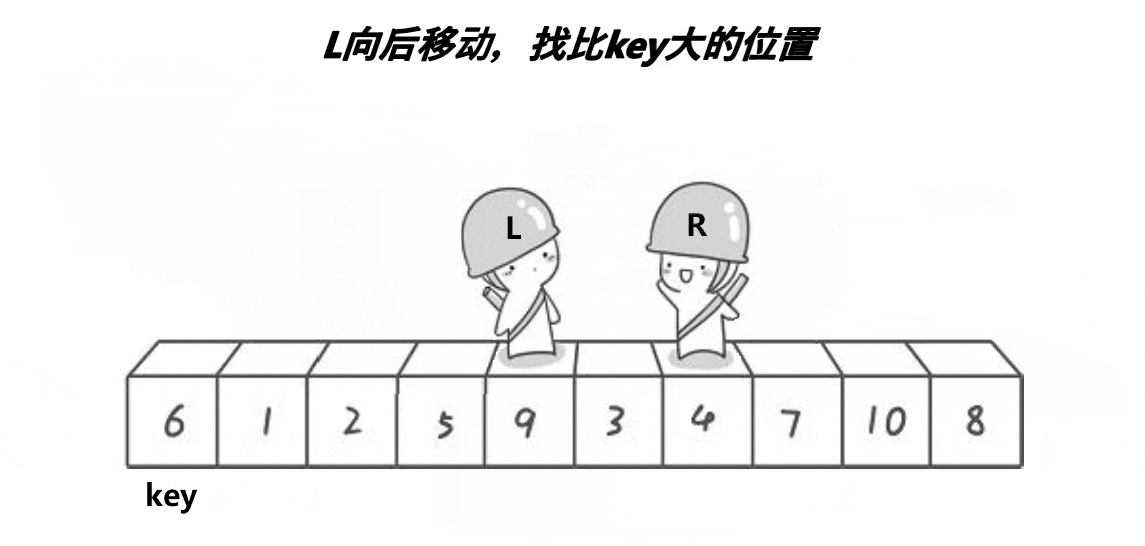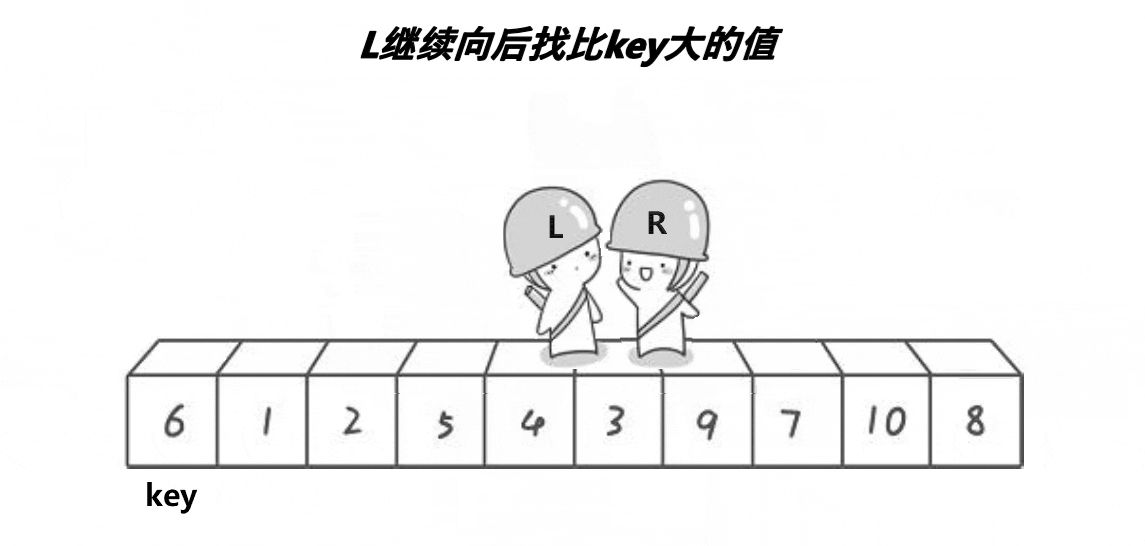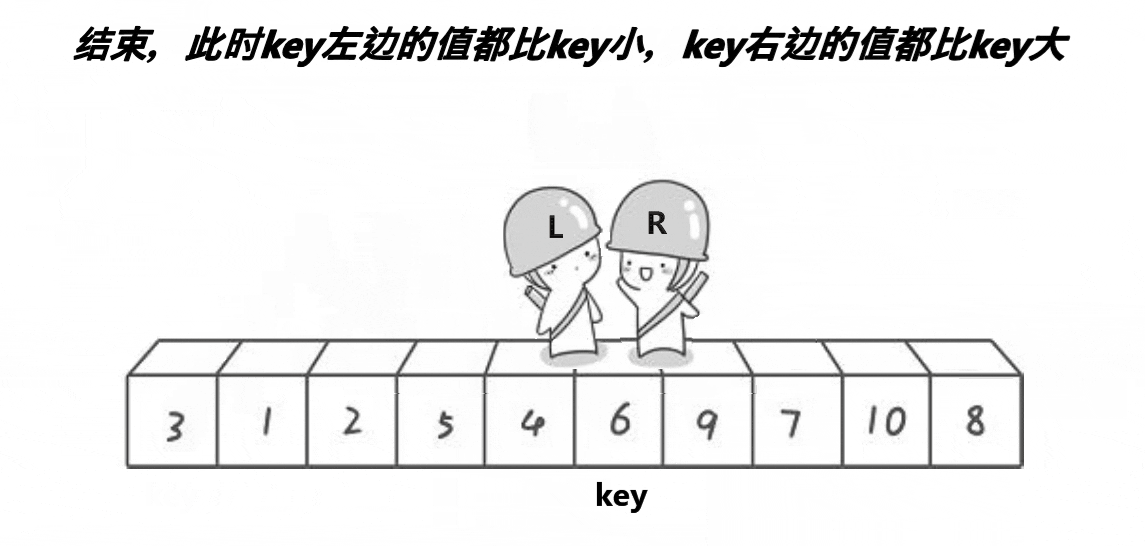
这个方法的思想就是R找比key小的数,L找比key大的数,然后将R和L对应的数交换,当R和L相遇时,将R和L对应的数与key交换,最终使得比key大的数都在key的右边,比key小的数都在key的左边。
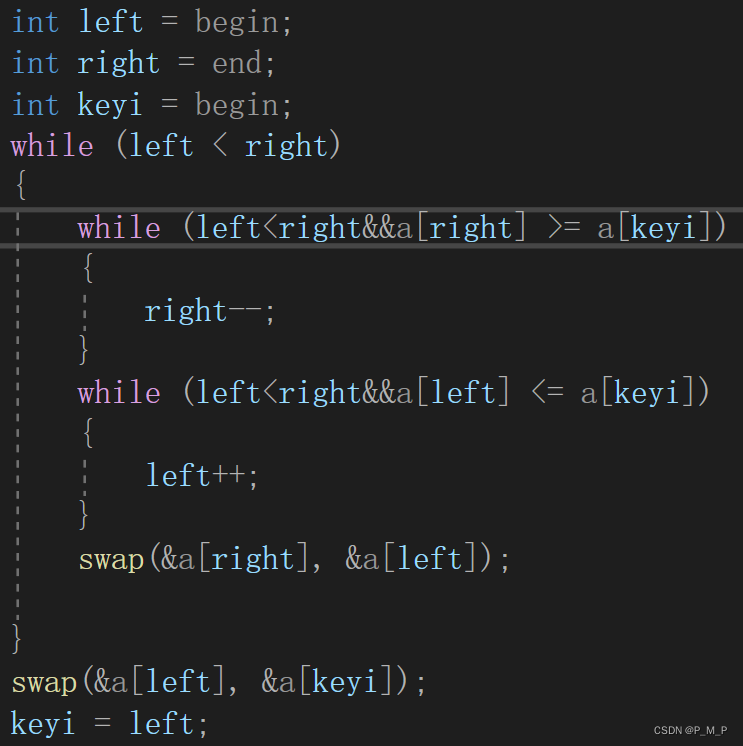
这里其实我们保存的时基准值的下标,记为keyi,这样做是为了方便交换,不然交换时只是与key这个临时变量发生了交换而没有影响到原来的数组里的数。
这里其实还有几个疑点:
- 当a[left],a[right]与a[keyi]相等时,怎么办?这里的处理方法其实就是不管它,直接继续原来的过程就可以了,最终两边排序时都会将这个数放到合理的位置。
- 为什么当R与L相遇时,它们所对应的数一定比a[keyi]小?要得到这个结论,必须要R先开始走,当R和L相遇时,有两种情况,一是L动的时候遇见R,此时R由于先走且一直在找比基准值小的数,所以当R停下时,R对应的数一定是小于等于基准值,L找比基准值大的数,一直没有找到,遇见R就停下来;二是R动的时候遇见L,R没有找到比key小的,所以一直走,又因为L一直在找比基准值大的数,所以当L停下时,L对应的数一定大于基准值,因此,只要R先走,R和L相遇时,对应的数一定比a[keyi]小。
⭐挖坑法
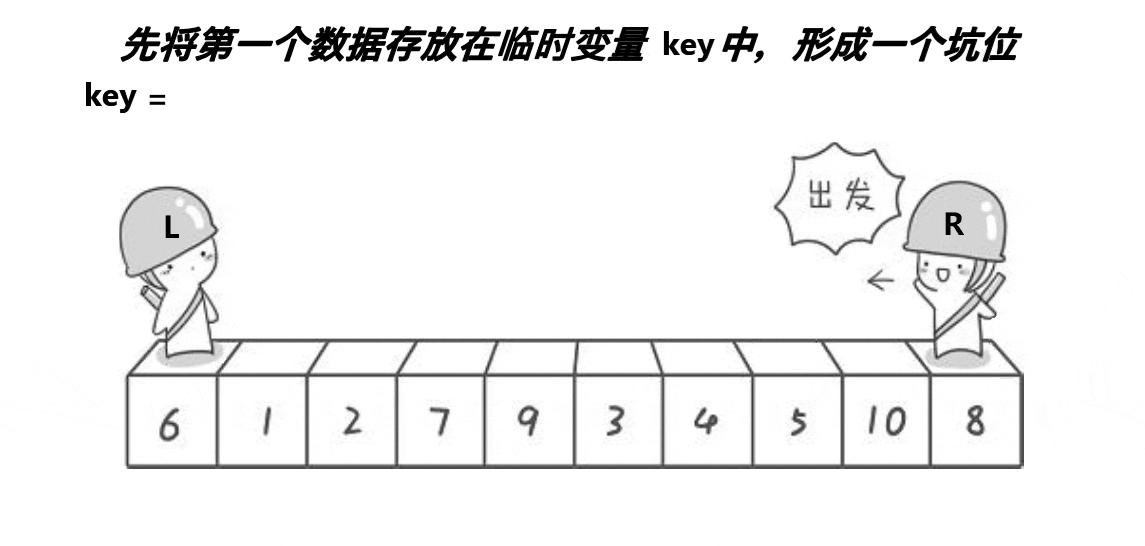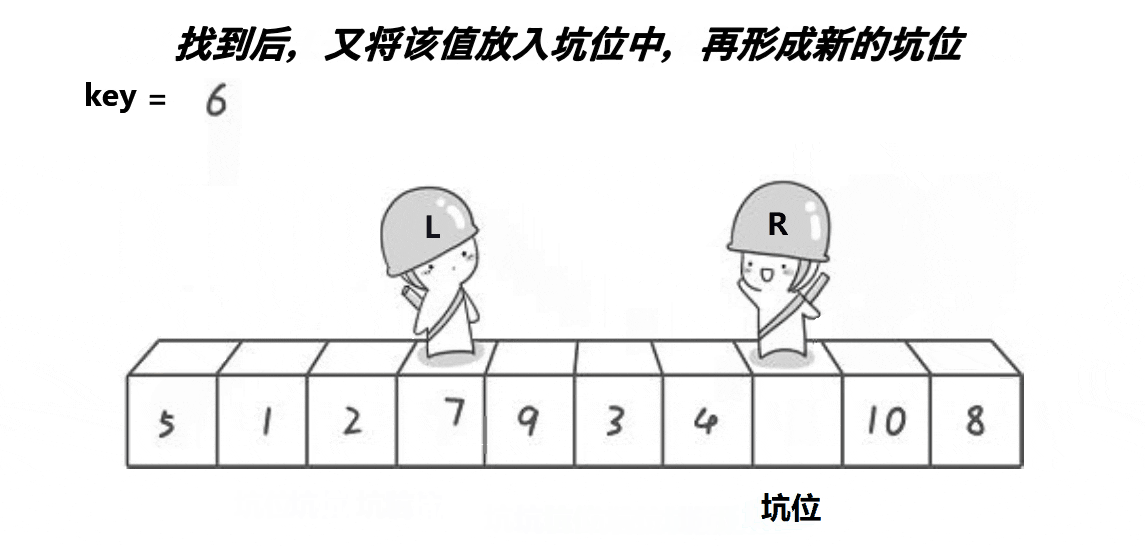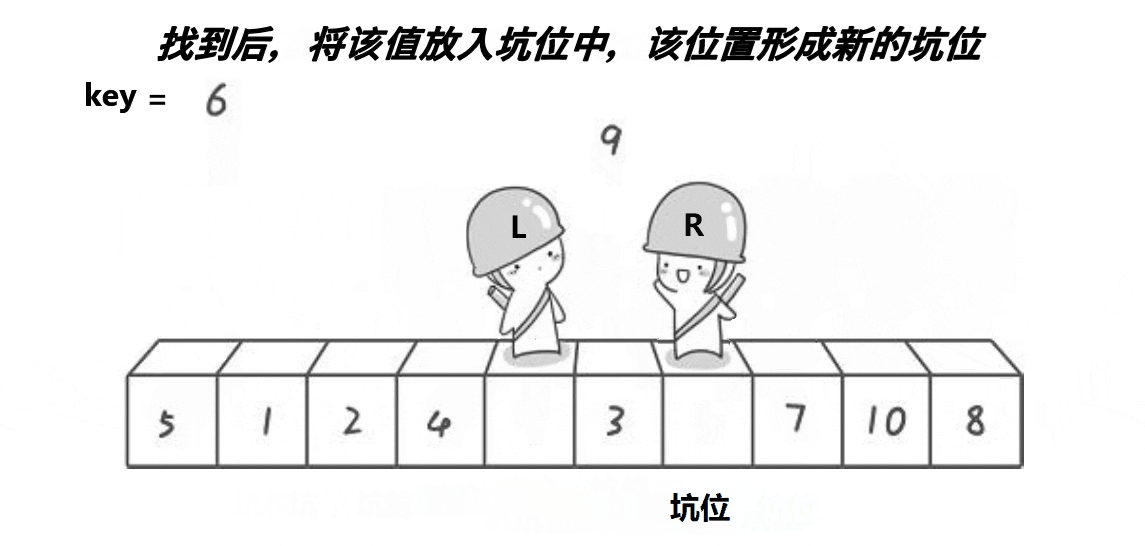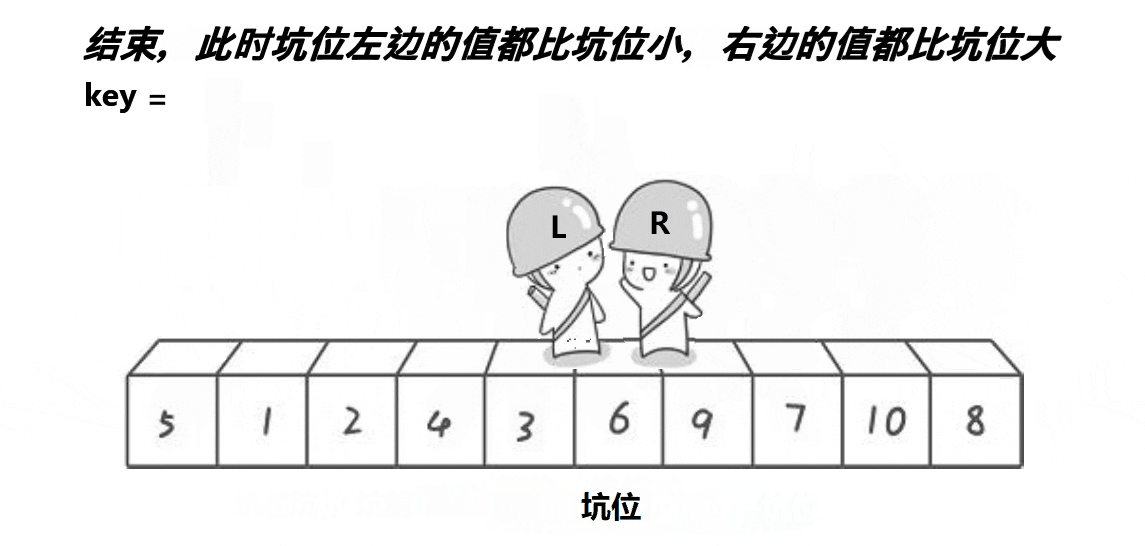
所谓挖坑法,就是第一次将基准值的位置设为坑(hole),然后R找比key小的数,填入到坑中,并使R对应的位置成为新的坑,然后L找比key大的数,填入到坑中,并使L对应的位置成为新的坑,再重复进行这个过程,当R和L相遇时,此时它们所对应的位置一定是一个坑,然后再将key填入到坑中,此时key左边的数一定比它小,key右边的数一定比他大。
这个方法相较于hoare的方法更加好理解,但是性能上并没有太大的变化。
//挖坑法
int PartSort(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);swap(&a[begin], &a[midi]);int key = a[begin];int hole = begin;while (begin < end){//右边找小,填到左边的坑while (begin < end && a[end] >= key){end--;}a[hole] = a[end];hole = end;//左边找大,填到右边的坑while (begin < end && a[begin] <= key){begin++;}a[hole] = a[begin];hole = begin;}a[hole] = key;return hole;
}⭐前后指针法
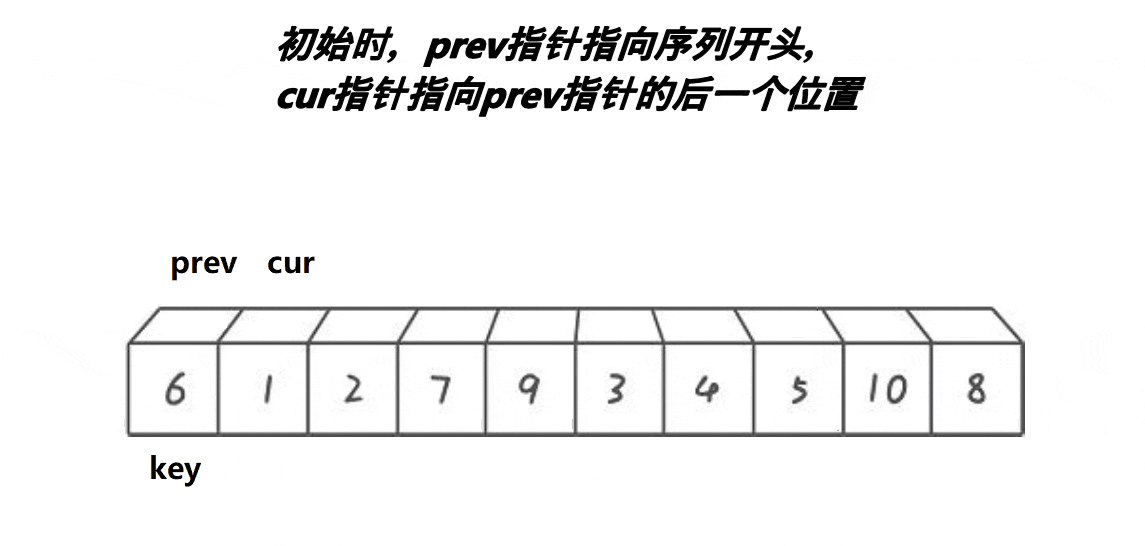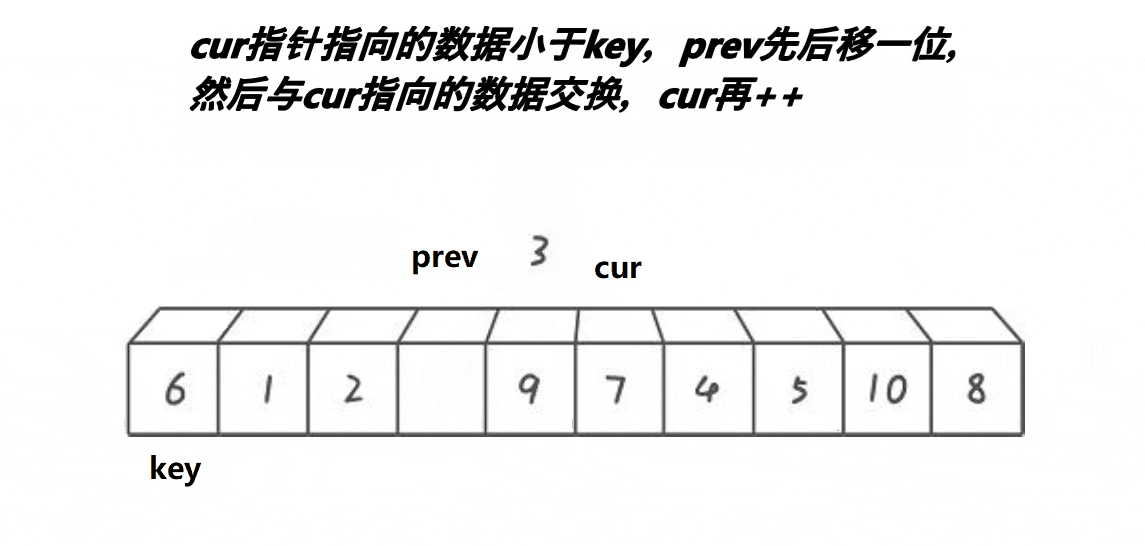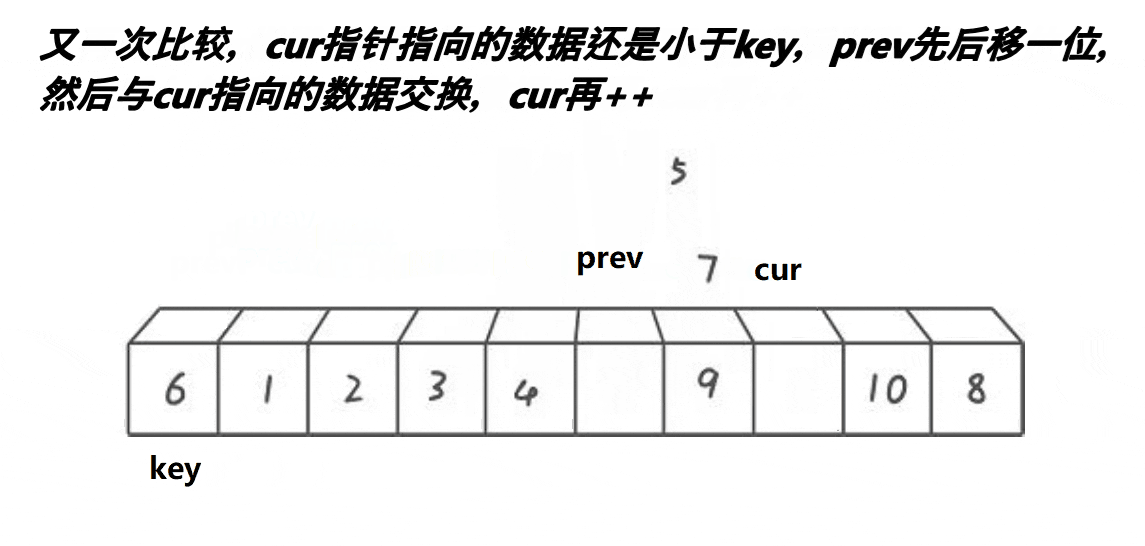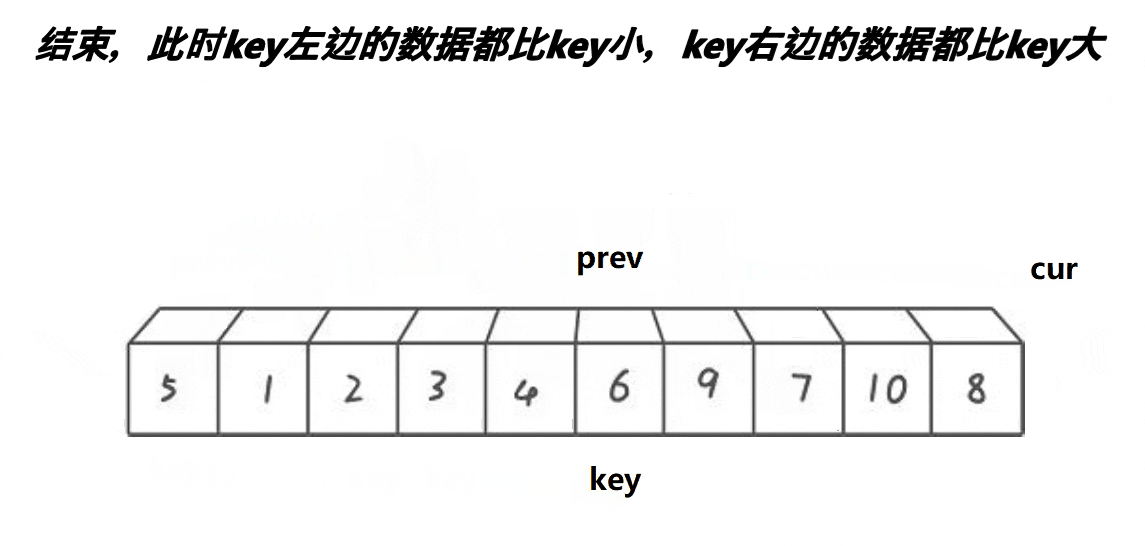
这个方法就是
- cur遇到比key大的数,cur++;
- cur遇到比key小的数,prev++,交换cur与prev位置的值,cur++。
- 当cur超出数组边界时,将prev位置的值与key位置的值交换。
int PartSort(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);swap(&a[begin], &a[midi]);int keyi = begin;int prev = begin;int cur = begin + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)//自身交换减少了{swap(&a[prev], &a[cur]);}cur++;}swap(&a[keyi], &a[prev]);keyi = prev;return prev;
}💡优化方法
⭐三数取中法
所谓三数取中法,其实取的是三个数中的中位数,将这个数作为基准值,能够避免某些极端情况的出现(比如数组已经接近有序)。
⚠注:这是针对基数选取进行的优化,另外还有随机数法选数,在这里就不过多介绍了。

int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;//取中位数if (a[begin] <= a[midi]){if (a[midi] <= a[end]){return midi;}else {if (a[begin] <= a[end])return end;elsereturn begin;}}else //midi begin{if (a[begin] >= a[end]){if (a[midi] >= end){return midi;}elsereturn end;}elsereturn begin;}
}⭐小区间内使用插入排序
在递归到较小区间时,如果仍然使用快速排序,会造成时间上的浪费,假如这个区间内有7个数,那就要递归7次才能得到这个7个数的有序序列。
if(end-begin+1 <= 10)
{//某个区间内的小规模排序直接插入排序//进行插入排序InsertSort(arr,end-begin+1);return;
}
💡非递归实现快速排序
非递归实现方法其实与递归的方法类似,但是需要借助栈这个数据结构(避免其他方法造成栈溢出)。
每次将要排序的区间的起始位置入栈,然后排序时再取栈顶的前两个元素作为一个排序区间进行快速排序,然后依次对key的左区间、右区间进行这样的操作,最终得到有序序列。
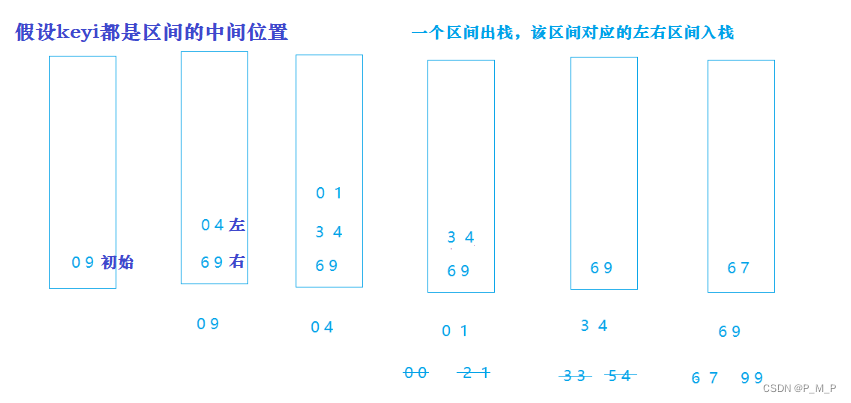
void QuickSortNonR(int* a, int begin, int end)
{ST s;STInit(&s);STPush(&s, end);STPush(&s, begin);while (!STEmpty(&s)){int left = STTop(&s);STPop(&s);int right = STTop(&s);STPop(&s);int keyi = PartSort(a, left, right);// [left, keyi-1] keyi [keyi+1, right]if (left < keyi - 1){STPush(&s, keyi - 1);STPush(&s, left);}if (keyi + 1 < right){STPush(&s, right);STPush(&s, keyi + 1);}}STDestroy(&s);
}💡性能分析
- 时间复杂度:最差O(N^2),最好O(NlogN),平均O(NlogN)
- 空间复杂度:O(logN),因为递归时创建的栈帧(申请的空间)没有销毁,递归的深度为logN
- 稳定性:不稳定
- 特点:数据越乱排序越快
相关文章:

深入理解——快速排序
目录 💡基本思想 💡基本框架 💡分割方法 ⭐Hoare版本 ⭐挖坑法 ⭐前后指针法 💡优化方法 ⭐三数取中法 ⭐小区间内使用插入排序 💡非递归实现快速排序 💡性能分析 💡基本思想 任取待排…...

【代码随想录】算法训练计划50
dp 1、123. 买卖股票的最佳时机 III 题目: 给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。 设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。 注意:你不能同时参与多笔交易(你必须在再次购…...
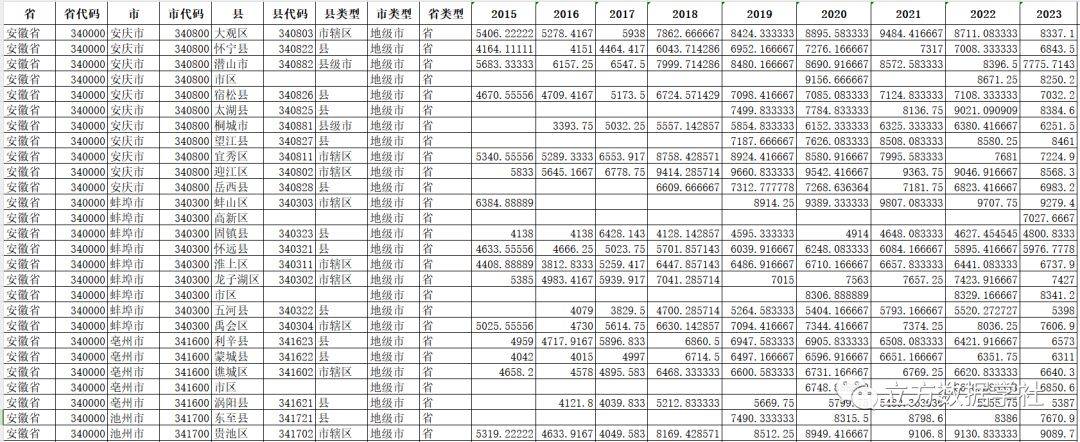
【数据分享】2019-2023年我国区县逐年二手房房价数据(Excel/Shp格式)
房价是一个区域发展程度的重要体现,一个区域的房价越高通常代表这个区域越发达,对于人口的吸引力越大!因此,房价数据是我们在各项城市研究中都非常常用的数据!之前我们分享了2019—2023年我国区县逐月的二手房房价数据…...
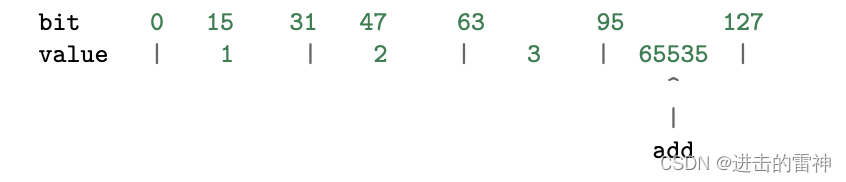
Redis设计与实现之整数集合
目录 一、内存映射数据结构 二、整数集合 1、整数集合的应用 2、数据结构和主要操作 3、intset运行实例 创建新intset 添加新元素到 intset 添加新元素到 intset(不需要升级) 添加新元素到 intset (需要升级) 4、升级 升级实例 5、关于升级 …...
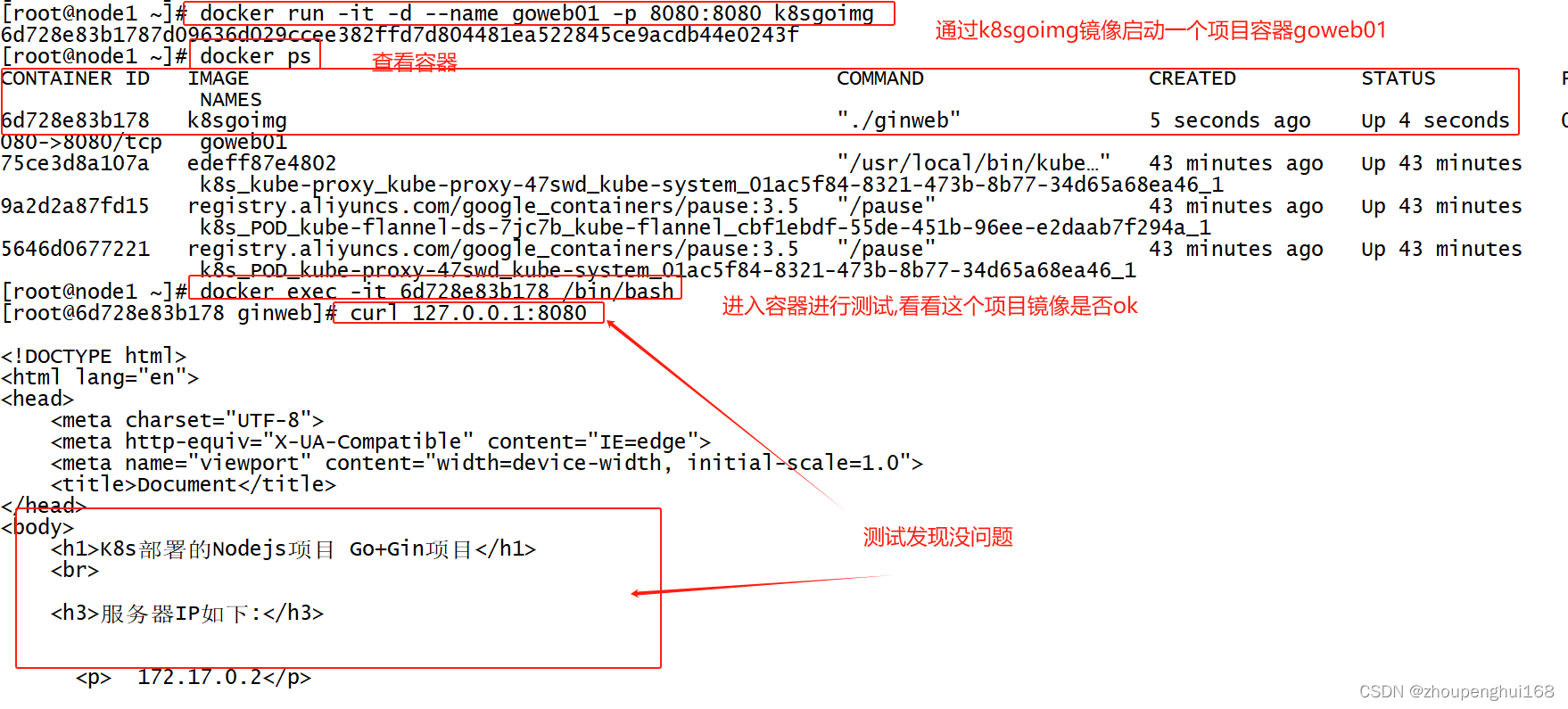
[Kubernetes]2. k8s集群中部署基于nodejs golang的项目以及Pod、Deployment详解
一. 创建k8s部署的镜像 1.部署nodejs项目 (1).上传nodejs项目到节点node1 (2).压缩nodejs项目 (3).构建nodejsDockerfile 1).创建nodejsDockerfile 具体可参考:[Docker]十.Docker Swarm讲解,在/root下创建nodejsDockerfile,具体代码如下: FROM node #把压缩文件COPY到镜像的…...
讯飞星火大模型api调用
讯飞星火大模型,通过websocket方式通信传递协议要求的报文,然后将流式返回的报文拼接为完整的响应内容,status2时是最后一条消息。因为是websocket方式所以是异步响应的,如果想要同步需要使用CountDownLatch控制下线程等待最后一条…...

TCP与UDP:网络世界中的“顺丰快递”与“广播电台”
随着互联网的普及,我们每天都在与网络打交道。而在这背后,数据的传输离不开TCP和UDP这两种传输协议。它们就像网络世界中的“顺丰快递”和“广播电台”,各自有着不同的工作方式和特点。让我们一起来了解一下它们吧! 一、TCP&…...

升级Xcode15,iOS17后问题解决
1、Could not build module ‘WebKit’ 报错 解决方案: 编辑文件 /Applications/Xcode.app/Contents/Developer/Platforms/iPhoneOS.platform/Developer/SDKs/iPhoneOS17.0.sdk/System/Library/Frameworks/WebKit.framework/Headers/WKWebsiteDataStore.h 将里面…...
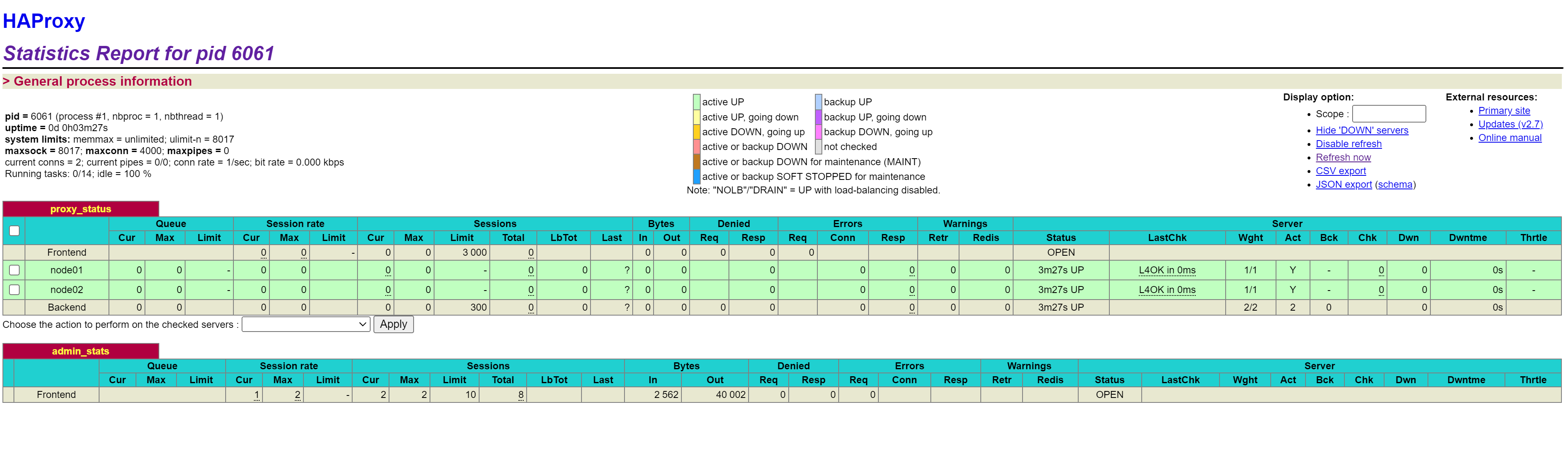
RabbitMQ搭建集群环境、配置镜像集群、负载均衡
RabbitMQ集群搭建 Linux安装RabbitMQ下载安装基本操作命令开启管理界面及配置 RabbitMQ集群搭建确定rabbitmq安装目录启动第一个节点启动第二个节点停止命令创建集群查看集群集群管理 RabbitMQ镜像集群配置启用HA策略创建一个镜像队列测试镜像队列 负载均衡-HAProxy安装HAProxy…...

leetcode:457. 环形数组是否存在循环
环形数组是否存在循环 存在一个不含 0 的 环形 数组 nums ,每个 nums[i] 都表示位于下标 i 的角色应该向前或向后移动的下标个数: 如果 nums[i] 是正数,向前(下标递增方向)移动 |nums[i]| 步 如果 nums[i] 是负数&…...

Kafka集成springboot
安装kafka,直接到官网下载bin文件,本文使用windows进行使用kafka。 下载之后,第一步,启动zookeeper: zookeeper-server-start.bat ..\..\config\zookeeper.properties 第二步,启动kafka: kafka…...

Unity中实现ShaderToy卡通火(移植篇)
文章目录 前言一、准备好我们的后处理基础脚本1、C#:2、Shader: 二、开始逐语句对ShaderToy进行转化1、首先,找到我们的主函数 mainImage2、其余的方法全部都是在 mainImage 函数中调用的方法3、替换后的代码(已经没报错了,但是效…...

指针相关知识(进阶)
前面的入门中已经介绍了指针的基础知识,接下来,让我们继续学习吧! 一. 字符指针变量 char* 一般形式 int main() {char n w;char* pa &n;*pa w;return 0; } 这并不是把字符串hello world放在n中,而是把第一个字符的地址…...

怎么将文件变为可执行文件
怎么将文件变为可执行文件 在Unix/Linux系统中,要将一个文件变为可执行文件,你需要使用chmod命令。以下是基本的步骤: 打开终端:使用你系统中的终端或命令行界面。 使用 cd 命令切换到包含你的文件的目录。例如: bash …...

5373. 中等计算
文章目录 QuestionIdeasCode Question 给定一个长度为 n 的非负整数序列 a1,a2,…,an 。 对于 1≤i≤n ,有 biai⊕(imod1)⊕(imod2)⊕…⊕(imodn) 。 请你计算并输出 b1⊕b2⊕…⊕bn 的值。 ⊕ 表示按位异或。 输入格式 第一行包含整数 n 。 第二行包含 n 个整…...

极智一周 | 两系列汇总、MI300X、H100、特供芯片、GPT-4、火灾检测、酷睿Ultra And so on
欢迎关注我的公众号 [极智视界],获取我的更多技术分享 大家好,我是极智视界,带来本周的 [极智一周],关键词:两系列汇总、MI300X、H100、特供芯片、GPT-4、火灾检测、酷睿Ultra And so on。 邀您加入我的知识星球「极智…...

leetcode刷题日志-383赎金信
思路:分别用两个map记录ransomNote和magazine中的字符以及出现的次数。最后遍历记录ransomNote的map,如果ransomNote的map中出现的magazine的map中没有出现或者出现的次数小于ransomNote的map则返回false,否则返回true; class So…...
—volume.md)
K8s(九)—volume.md
目录 volumeconfigMap介绍官网例子基于文件生成 ConfigMap使用 ConfigMap 数据定义容器环境变量使用单个 ConfigMap 中的数据定义容器环境变量 EmptyDirhostPathhostPath 配置示例 nfspersistentVolumeClaim volume https://kubernetes.io/zh-cn/docs/concepts/storage/volume…...

python N个人围成一圈报数 报到3出列 直到只剩下最后一人
公司聚会上,N名员工围成一圈,按1—N顺序编号(要求N<40)。 然后从队头开始1,2,3报数,数3的出列,剩下的员工再从头开始1,2,3报数……直到剩下最后一名员工时, 这员工就是…...

RFC4861 中文版下
10. 协议常量 路由器常量: MAX_INITIAL_RTR_ADVERT_INTERVAL 16 秒MAX_INITIAL_RTR_ADVERTISEMENTS 3 次发送MAX_FINAL_RTR_ADVERTISEMENTS 3 次发送MIN_DELAY_BETWEEN_RAS 3 秒MAX_RA_DELAY_TIME .5 秒主机常量: MAX_RTR_SOLICITATION_…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
