leetcode:457. 环形数组是否存在循环
- 环形数组是否存在循环
存在一个不含 0 的 环形 数组 nums ,每个 nums[i] 都表示位于下标 i 的角色应该向前或向后移动的下标个数:
如果 nums[i] 是正数,向前(下标递增方向)移动 |nums[i]| 步
如果 nums[i] 是负数,向后(下标递减方向)移动 |nums[i]| 步
因为数组是 环形 的,所以可以假设从最后一个元素向前移动一步会到达第一个元素,而第一个元素向后移动一步会到达最后一个元素。
数组中的 循环 由长度为 k 的下标序列 seq 标识:
遵循上述移动规则将导致一组重复下标序列 seq[0] -> seq[1] -> … -> seq[k - 1] -> seq[0] -> …
所有 nums[seq[j]] 应当不是 全正 就是 全负
k > 1
如果 nums 中存在循环,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,-1,1,2,2]
输出:true
解释:存在循环,按下标 0 -> 2 -> 3 -> 0 。循环长度为 3 。
示例 2:
输入:nums = [-1,2]
输出:false
解释:按下标 1 -> 1 -> 1 … 的运动无法构成循环,因为循环的长度为 1 。根据定义,循环的长度必须大于 1 。
示例 3:
输入:nums = [-2,1,-1,-2,-2]
输出:false
解释:按下标 1 -> 2 -> 1 -> … 的运动无法构成循环,因为 nums[1] 是正数,而 nums[2] 是负数。
所有 nums[seq[j]] 应当不是全正就是全负。
提示:
1 <= nums.length <= 5000
-1000 <= nums[i] <= 1000
nums[i] != 0
进阶:你能设计一个时间复杂度为 O(n) 且额外空间复杂度为 O(1) 的算法吗?
方法:快慢指针
思路:我们可以将环形数组理解为图中的 n 个点,nums[i]表示 i号点向 (i+nums[i])mod n 号点连有一条单向边。
注意到这张图中的每个点有且仅有一条出边,这样我们从某一个点出发,沿着单向边不断移动,最终必然会进入一个环中。而依据题目要求,我们要检查图中是否存在一个所有单向边方向一致的环。
具体地,我们检查每一个节点,令快慢指针从当前点出发,快指针每次移动两步,慢指针每次移动一步,期间每移动一次,我们都需要检查当前单向边的方向是否与初始方向是否一致,如果不一致,我们即可停止遍历,因为当前路径必然不满足条件。为了降低时间复杂度,我们可以标记每一个点是否访问过,过程中如果我们的下一个节点为已经访问过的节点,则可以停止遍历。
class Solution {
public:bool circularArrayLoop(vector<int>& nums) {int n = nums.size();// 将lambda表达式作为函数对象auto next_index = [&](int cur) {//保证返回值在 [0, n)return ((cur + nums[cur]) % n + n) % n;};// 依次检查各个节点for (int i = 0; i < n; i++) {if (0 == nums[i]) {continue;}int slow = i;int fast = next_index(i);// 判断非零且方向相同while (nums[slow] * nums[fast] > 0 && nums[slow] * nums[next_index(fast)] > 0) {if (slow == fast) {if (slow != next_index(slow)) {// 从这个节点开始,存在环,返回return true;} else {// 当nums[i]为n的整倍数时,i的后继节点即为i本身,此时循环长度k=1,不符合题目要求break;}}slow = next_index(slow);fast = next_index(next_index(fast));}// 从这个节点开始,不存在环,将遍历过的节点置为0,为下一次遍历做准备int add = i;while (nums[add] * nums[next_index(add)] > 0) {nums[add] = 0;add = next_index(add);}}return false;}
};
相关文章:

leetcode:457. 环形数组是否存在循环
环形数组是否存在循环 存在一个不含 0 的 环形 数组 nums ,每个 nums[i] 都表示位于下标 i 的角色应该向前或向后移动的下标个数: 如果 nums[i] 是正数,向前(下标递增方向)移动 |nums[i]| 步 如果 nums[i] 是负数&…...

Kafka集成springboot
安装kafka,直接到官网下载bin文件,本文使用windows进行使用kafka。 下载之后,第一步,启动zookeeper: zookeeper-server-start.bat ..\..\config\zookeeper.properties 第二步,启动kafka: kafka…...

Unity中实现ShaderToy卡通火(移植篇)
文章目录 前言一、准备好我们的后处理基础脚本1、C#:2、Shader: 二、开始逐语句对ShaderToy进行转化1、首先,找到我们的主函数 mainImage2、其余的方法全部都是在 mainImage 函数中调用的方法3、替换后的代码(已经没报错了,但是效…...

指针相关知识(进阶)
前面的入门中已经介绍了指针的基础知识,接下来,让我们继续学习吧! 一. 字符指针变量 char* 一般形式 int main() {char n w;char* pa &n;*pa w;return 0; } 这并不是把字符串hello world放在n中,而是把第一个字符的地址…...

怎么将文件变为可执行文件
怎么将文件变为可执行文件 在Unix/Linux系统中,要将一个文件变为可执行文件,你需要使用chmod命令。以下是基本的步骤: 打开终端:使用你系统中的终端或命令行界面。 使用 cd 命令切换到包含你的文件的目录。例如: bash …...

5373. 中等计算
文章目录 QuestionIdeasCode Question 给定一个长度为 n 的非负整数序列 a1,a2,…,an 。 对于 1≤i≤n ,有 biai⊕(imod1)⊕(imod2)⊕…⊕(imodn) 。 请你计算并输出 b1⊕b2⊕…⊕bn 的值。 ⊕ 表示按位异或。 输入格式 第一行包含整数 n 。 第二行包含 n 个整…...

极智一周 | 两系列汇总、MI300X、H100、特供芯片、GPT-4、火灾检测、酷睿Ultra And so on
欢迎关注我的公众号 [极智视界],获取我的更多技术分享 大家好,我是极智视界,带来本周的 [极智一周],关键词:两系列汇总、MI300X、H100、特供芯片、GPT-4、火灾检测、酷睿Ultra And so on。 邀您加入我的知识星球「极智…...

leetcode刷题日志-383赎金信
思路:分别用两个map记录ransomNote和magazine中的字符以及出现的次数。最后遍历记录ransomNote的map,如果ransomNote的map中出现的magazine的map中没有出现或者出现的次数小于ransomNote的map则返回false,否则返回true; class So…...
—volume.md)
K8s(九)—volume.md
目录 volumeconfigMap介绍官网例子基于文件生成 ConfigMap使用 ConfigMap 数据定义容器环境变量使用单个 ConfigMap 中的数据定义容器环境变量 EmptyDirhostPathhostPath 配置示例 nfspersistentVolumeClaim volume https://kubernetes.io/zh-cn/docs/concepts/storage/volume…...

python N个人围成一圈报数 报到3出列 直到只剩下最后一人
公司聚会上,N名员工围成一圈,按1—N顺序编号(要求N<40)。 然后从队头开始1,2,3报数,数3的出列,剩下的员工再从头开始1,2,3报数……直到剩下最后一名员工时, 这员工就是…...

RFC4861 中文版下
10. 协议常量 路由器常量: MAX_INITIAL_RTR_ADVERT_INTERVAL 16 秒MAX_INITIAL_RTR_ADVERTISEMENTS 3 次发送MAX_FINAL_RTR_ADVERTISEMENTS 3 次发送MIN_DELAY_BETWEEN_RAS 3 秒MAX_RA_DELAY_TIME .5 秒主机常量: MAX_RTR_SOLICITATION_…...
用友时空 KSOA 多处SQL注入漏洞复现
0x01 产品简介 用友时空 KSOA 是建立在 SOA 理念指导下研发的新一代产品,是根据流通企业前沿的 IT 需求推出的统一的IT基础架构,它可以让流通企业各个时期建立的 IT 系统之间彼此轻松对话。 0x02 漏洞概述 用友时空 KSOA 系统 PayBill、QueryService、linkadd.jsp等接口处…...

[AutoSar]基础部分 RTE 介绍
目录 关键词平台说明一、什么是RTE二、RTE的主要功能 关键词 嵌入式、C语言、autosar、EcuM、wakeup、flex 平台说明 项目ValueOSautosar OSautosar厂商vector芯片厂商TI编程语言C,C编译器HighTec (GCC) 一、什么是RTE RTE(Run-Time Environment&…...
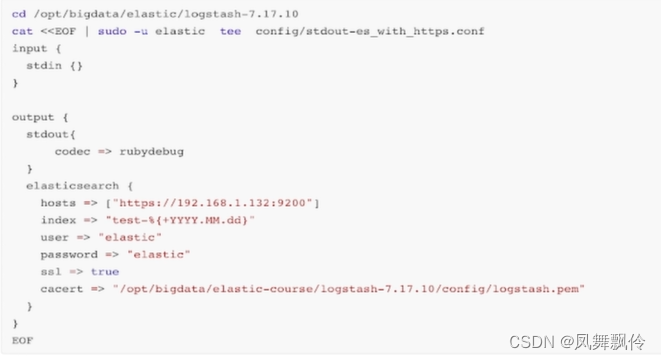
Logstash访问安全访问Elasticsearch集群
生成logstash证书: opensal pkcs12 -in elastic-stack-ca.p12 -clcerts -nokeys > logafash.cer openssl x509 -in logstash.cer -out logstash.pem 编排配置文件...
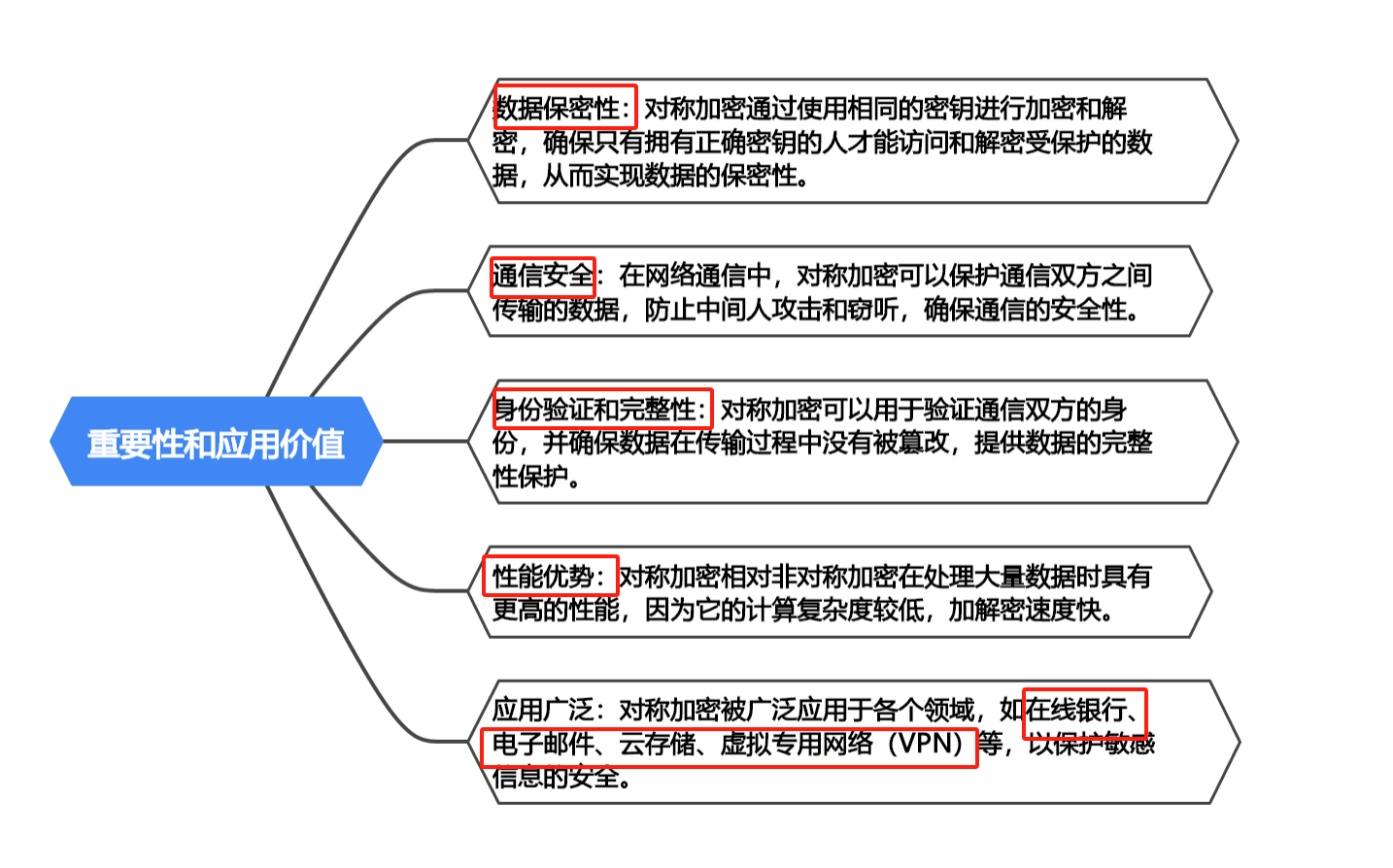
加密的艺术:对称加密的奇妙之处(下)
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...
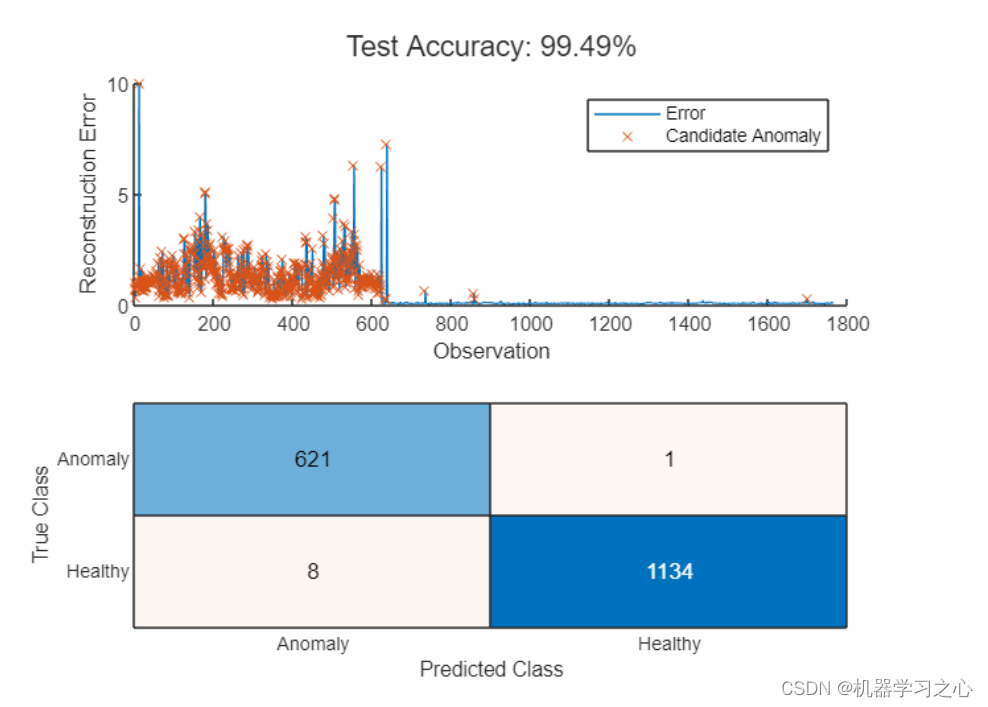
异常检测 | MATLAB实现BiLSTM(双向长短期记忆神经网络)数据异常检测
异常检测 | MATLAB实现BiLSTM(双向长短期记忆神经网络)数据异常检测 目录 异常检测 | MATLAB实现BiLSTM(双向长短期记忆神经网络)数据异常检测效果一览基本介绍模型准备模型设计参考资料效果一览 基本介绍 训练一个双向 LSTM 自动编码器来检测机器是否正常工作。 自动编码器接受…...
)
2023“楚怡杯”湖南省赛“信息安全管理与评估“--数字取证调查(高职组)
2023“楚怡杯”湖南省“信息安全管理与评估”(高职组)任务书 2023“楚怡杯”湖南省“信息安全管理与评估”(高职组)任务书第一阶段竞赛项目试题第二阶段竞赛项目试题第二部分 数字取证调查:需要环境私聊博主:2023“楚怡杯”湖南省“信息安全管理与评估”(高职组)任务书…...
C++ list常用操作
目录 一、介绍 二、list的常用操作 1、构造 2、迭代器 3、元素访问 4、容量操作 一、介绍 std::list文档链接 list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。list的底层是双向链表结构,双向链表中每个…...

MILP加速运算技巧——模型对称性的预处理
文章目录 整数规划的对称性什么是对称性对称性的影响 对称性的预处理方法 整数规划的对称性 什么是对称性 许多整数规划问题存在对称性,这种对称性是指问题解空间的对称,即在对称的解空间当中解的优化目标值上是相同的。这种对称性并不会改变问题的最优…...

JavaScript中的生成器与迭代器详解
一、迭代器与可迭代对象 1.什么是迭代器 迭代器(iterator),使用户在容器对象(container,例如链表或数组)上遍访的对象,使用该接口无需关心对象的内部实现细节。 其行为像数据库中的光标&…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...

vue3 手动封装城市三级联动
要做的功能 示意图是这样的,因为后端给的数据结构 不足以使用ant-design组件 的联动查询组件 所以只能自己分装 组件 当然 这个数据后端给的不一样的情况下 可能组件内对应的 逻辑方式就不一样 毕竟是 三个 数组 省份 城市 区域 我直接粘贴组件代码了 <temp…...

盲盒一番赏小程序:引领盲盒新潮流
在盲盒市场日益火爆的今天,如何才能在众多盲盒产品中脱颖而出?盲盒一番赏小程序给出了答案,它以创新的玩法和优质的服务,引领着盲盒新潮流。 一番赏小程序的最大特色在于其独特的赏品分级制度。赏品分为多个等级,从普…...

< 自用文 OS有关 新的JD云主机> 国内 京东云主机 2C4G 60G 5Mb 498/36月 Ubuntu22
攒了这么久,废话一些: 前几周很多事儿,打算回北京,开个清真的德克萨斯烤肉店,写了一篇 : < 自用文 Texas style Smoker > 美式德克萨斯烟熏炉 从设计到实现 (第一部分&…...

1.springmvc基础入门(一)
1.Spring MVC概念 Spring MVC 是 Spring Framework 提供的 Web 组件,全称是 Spring Web MVC,是⽬前主流的实现 MVC 设计模式的框架,提供前端路由映射、视图解析等功能。 Java Web 开发者必须要掌握的技术框架。 2.Spring MVC 功能 MVC&am…...
