MILP加速运算技巧——模型对称性的预处理
文章目录
- 整数规划的对称性
- 什么是对称性
- 对称性的影响
- 对称性的预处理方法
整数规划的对称性
什么是对称性
许多整数规划问题存在对称性,这种对称性是指问题解空间的对称,即在对称的解空间当中解的优化目标值上是相同的。这种对称性并不会改变问题的最优值,如果我们能够限制这种对称性,就能在不改变问题最优值的情况下,缩减问题可行空间的规模,因此很多MIP求解器会对模型的对称性做出检测并进行处理。
以生产排程问题为例,加入存在一批加工工件,每个工件基于它的产品类型有一个加工工艺,若工件1和工件2的加工工艺相同,此时,对于最终的生产方案而言,加工工件1和加工工件2的每个步骤的顺序进行调换,并不会影响问题的目标值,此时工件1和工件2相关的所有决策变量具有对称性。
又例如: 2 x 1 + 2 x 2 + x 3 ≤ 10 , x 1 ≤ 5 , x 2 ≤ 5 2x1+2x2+x3\leq 10, x1\leq 5, x2\leq 5 2x1+2x2+x3≤10,x1≤5,x2≤5,目标函数是 3 x 1 + 3 x 2 + x 3 3x1+3x2+x3 3x1+3x2+x3,此时不论最终的结果如何, x 1 , x 2 x1,x2 x1,x2之间的解进行调换,都不会影响目标值,原因是 x 1 , x 2 x1,x2 x1,x2 不论是约束系数,还是边界,以及目标函数系数都相同,他们的最优解互相对调,也是一个最优解,两个变量具有对称性。
例如以Gurobi预处理为例:
# 添加约束
model.addConstr(2*x1+ 2*x2 + y <= 10)
model.addConstr(x1 <= 5)
model.addConstr(x2 <= 5)
model.addConstr(y >= 5)
# 定义目标函数
model.setObjective(3*x1 +3*x2 + y, sense=grb.GRB.MINIMIZE)
在求解日志当中,上述问题的所有约束和变量都被预处理过程确定下来,当 y y y 确定后, x 1 + x 2 x1+x2 x1+x2 的值能确定,且由于 x 1 , x 2 x1,x2 x1,x2 两个变量对称,所以问题的最优解不唯一。
...
Presolve removed 4 rows and 3 columns
Presolve time: 0.00s
Presolve: All rows and columns removed
...
许多的整数规划问题当中都存在这样的特点,例如在车辆路径问题当中,有两个点到其他所有点的距离都一样,此时这两个点不论先通过哪个点都是一样的,但在求解问题当中,其中一个点在前的方案、以及另一个点在前的方案都包含在问题的可行域内,尽管两者是等价的。
对称性的影响
很显然,过于强烈的对称性有时候就会产生无效的搜索动作。特别是对于经典的精确搜索框架——分支定界,对称的变量会导致大量重复的待搜索节点(子问题),不论是界的收敛还是待剪支数量,对称性都会在这个过程中造成大量的无效动作。而这种具有对称性的等价变量越多,则问题当中等价的可行解就越多,相同节点也就越多,算法的搜索就会变慢。
对于一些问题而言,因为对称性导致原本不复杂的问题,往往难以直接通过求解器在可接受的时间内得到满意的解,因此对于这个混合整数变量的问题,需要采取一定的办法进行处理。
对称性的预处理方法
前面提到,这种等价变量的一个特点就是约束系数以及目标函数系数都一致,因此需要打破这种对称性,而这只需要改变系数的一致性即可,对于一些问题而言,这个动作能直接将求解问题的时间缩短几十上千倍。
一些求解器会建立具有任意目标函数系数的模型,而更一般性的方法是增加对称性割,即添加破坏这种对称性的约束条件:既然这些变量是等价变量,那就增加约束来使得这些变量的值不等价,有一个倾向性,减少算法搜索另一些等价的对称解空间,以此来提升算法效率,这对于大规模的且有大量等价变量的问题尤为重要。
对称性割的基本形式为:
d ⊤ x ≤ d ⊤ π ( x ) d^{\top}x \leq d^{\top}\pi (x) d⊤x≤d⊤π(x)
其中, π \pi π是置换算子, d = ( 2 n − 1 , 2 x − 2 , . . . 2 0 ) d=(2^{n-1}, 2^{x-2},...2^0) d=(2n−1,2x−2,...20), n n n 是具有对称性的等价变量数量。例如当 n = 2 n=2 n=2,只有 x 1 , x 2 x1,x2 x1,x2 两个等价变量时,对称性割就为 x 1 + 2 x 2 ≤ x 2 + 2 x 1 x1+2x2\leq x2+2x1 x1+2x2≤x2+2x1,移项得 x 2 ≤ x 1 x2\leq x1 x2≤x1。这种约束就使得原本等价的两个解,只能有一个是满足该约束的,缩减了问题的解空间,加速了B&B算法的收敛。但值得注意的是,有大量等价变量不仅意味着对称性割的加速效果显著,也意味着添加的对称性割的数量庞大,减少了相同的节点,但增加了节点处问题的求解难度,在实际中仍需要进行一定的权衡。
相关文章:

MILP加速运算技巧——模型对称性的预处理
文章目录 整数规划的对称性什么是对称性对称性的影响 对称性的预处理方法 整数规划的对称性 什么是对称性 许多整数规划问题存在对称性,这种对称性是指问题解空间的对称,即在对称的解空间当中解的优化目标值上是相同的。这种对称性并不会改变问题的最优…...

JavaScript中的生成器与迭代器详解
一、迭代器与可迭代对象 1.什么是迭代器 迭代器(iterator),使用户在容器对象(container,例如链表或数组)上遍访的对象,使用该接口无需关心对象的内部实现细节。 其行为像数据库中的光标&…...

WebLangChain_ChatGLM:结合 WebLangChain 和 ChatGLM3 的中文 RAG 系统
WebLangChain_ChatGLM 介绍 本文将详细介绍基于网络检索信息的检索增强生成系统,即 WebLangChain。通过整合 LangChain,成功将大型语言模型与最受欢迎的外部知识库之一——互联网紧密结合。鉴于中文社区中大型语言模型的蓬勃发展,有许多可供利…...

hive常用SQL函数及案例
1 函数简介 Hive会将常用的逻辑封装成函数给用户进行使用,类似于Java中的函数。 好处:避免用户反复写逻辑,可以直接拿来使用。 重点:用户需要知道函数叫什么,能做什么。 Hive提供了大量的内置函数,按照其特…...

分页操作中使用LIMIT和OFFSET后出现慢查询的原因分析
事情经过 最近在做批量数据处理的相关业务,在和下游对接时,发现拉取他们的业务数据刚开始很快,后面会越来越慢,40万数据一个小时都拉不完。经过排查后,发现对方用了很坑的分页查询方式 —— LIMIT OFFSET,…...

Java八股文面试全套真题【含答案】- Redis篇
请看下面列举的50个关于Redis的经典面试问题和简短答案: Redis是什么?简要介绍一下Redis的特点。 Redis是一个开源的高性能键值存储数据库,支持多种数据结构,如字符串、列表、集合、哈希和有序集合等。 特点包括快速、可持久化、支…...

【C++11特性篇】一文助小白轻松理解 C++中的【左值&左值引用】【右值&右值引用】
前言 大家好吖,欢迎来到 YY 滴C系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 主要内容含: 欢迎订阅 YY滴C专栏!更多干货持续更新!以下是传送门! 目录 一.【左值&左值引用】&…...
动态规划——OJ题(一)
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、第N个泰波那契数1、题目讲解2、思路讲解3、代码实现 二、三步问题1、题目讲解2、思路讲解…...
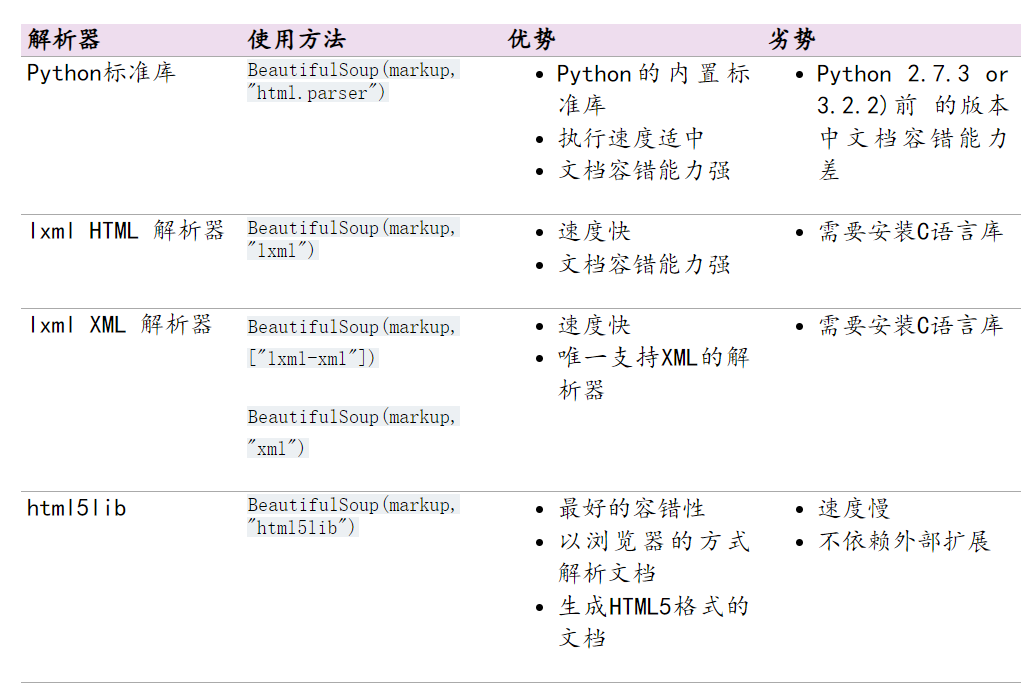
六:爬虫-数据解析之BeautifulSoup4
六:bs4简介 基本概念: 简单来说,Beautiful Soup是python的一个库,最主要的功能是从网页抓取数据官方解释如下: Beautiful Soup提供一些简单的、python式的函数用来处理导航、搜索、修改分析树等功能。 它是一个工具箱…...

音频筑基:总谐波失真THD+N指标
音频筑基:总谐波失真THDN指标 THDN含义深入理解 在分析音频信号中,THDN指标是我们经常遇到的概念,这里谈谈自己的理解。 THDN含义 首先,理解THD的定义: THD,Total Harmonic Distortion,总谐波…...
自动驾驶技术:驶向未来的智能之路
导言 自动驾驶技术正引领着汽车产业向着更安全、高效、智能的未来演进。本文将深入研究自动驾驶技术的核心原理、关键技术、应用场景以及对交通、社会的深远影响。 1. 简介 自动驾驶技术是基于先进传感器、计算机视觉、机器学习等技术的创新,旨在实现汽车在不需要人…...

TIGRE: a MATLAB-GPU toolbox for CBCT image reconstruction
TIGRE: 用于CBCT图像重建的MATLAB-GPU工具箱 论文链接:https://iopscience.iop.org/article/10.1088/2057-1976/2/5/055010 项目链接:https://github.com/CERN/TIGRE Abstract 本文介绍了基于层析迭代GPU的重建(TIGRE)工具箱,这是一个用于…...

我的NPI项目之Android 安全系列 -- EMVCo
最近一直在和支付有关的内容纠缠,原来我负责的产品后面还要过EMVCo的认证。于是,就网上到处找找啥事EMVCo,啥是EMVCo,啥是EMVCo。 于是找到了一个神奇的个人网站:Ganeshji Marwaha 虽然时间有点久远,但是用…...
vue中实现使用相框点击拍照,canvas进行前端图片合并下载
拍照和相框合成,下载图片dome 一、canvas介绍 Canvas是一个HTML5元素,它提供了一个用于在网页上绘制图形、图像和动画的2D渲染上下文。Canvas可以用于创建各种图形,如线条、矩形、圆形、文本等,并且可以通过JavaScript进行编程操作。 Canvas元素本身是一个矩形框,可以通…...

边缘检测@获取labelme标注的json黑白图掩码mask
import cv2 as cv import numpy as np import json import os from PIL import Imagedef convertPolygonToMask(jsonfilePath):...

嵌入式培训-数据结构-day23-线性表
线性表 线性表是包含若干数据元素的一个线性序列 记为: L(a0, ...... ai-1, ai, ai1 ...... an-1) L为表名,ai (0≤i≤n-1)为数据元素; n为表长,n>0 时,线性表L为非空表,否则为空表。 线性表L可用二元组形式描述…...
C# DotNetCore AOP简单实现
背景 实际开发中业务和日志尽量不要相互干扰嵌套,否则很难维护和调试。 示例 using System.Reflection;namespace CSharpLearn {internal class Program{static void Main(){int age 25;string name "bingling";Person person new(age, name);Conso…...

19.Tomcat搭建
Tomcat 简介 Tomcat的安装和启动 前置条件 • JDK 已安装(JAVA_HOME环境变量已被成功配置) Windows 下安装 访问 http://tomcat.apache.org ⇒ 左侧边栏 “Download” 2. 解压缩下载的文件到 “D:\tomcat”, tomcat的内容最终被解压到 “D:\tomcat\apache-tomcat-9.0.84” 3.…...

HarmonyOS云开发基础认证考试满分答案(100分)【全网最全-不断更新】【鸿蒙专栏-29】
系列文章: HarmonyOS应用开发者基础认证满分答案(100分) HarmonyOS应用开发者基础认证【闯关习题 满分答案】 HarmonyOS应用开发者高级认证满分答案(100分) HarmonyOS云开发基础认证满分答案(100分…...

Unity项目里Log系统该怎么设计
其实并没有想完整就设计一个好用的Log系统,然后发出来。记录这个的原因,是在书里看到这么一句话,Log会消耗资源,特别是写文件,因此可以设置一个Log缓冲区,等缓冲区满了再一次性写入文件,以节省资…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
