动态规划——OJ题(一)

文章目录
- 一、第N个泰波那契数
- 1、题目讲解
- 2、思路讲解
- 3、代码实现
- 二、三步问题
- 1、题目讲解
- 2、思路讲解
- 3、代码实现
- 三、使用最小花费爬楼梯
- 1、题目讲解
- 2、思路讲解
- 3、代码实现
- 四、解码方法
- 1、题目讲解
- 2、思路讲解
- 3、代码实现
一、第N个泰波那契数
1、题目讲解

2、思路讲解
- 状态表⽰:
这道题可以「根据题⽬的要求」直接定义出状态表⽰:
dp[i] 表⽰:第 i 个泰波那契数的值。 - 状态转移⽅程:
题⽬已经⾮常贴⼼的告诉我们了:
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] - 初始化:
从我们的递推公式可以看出, dp[i] 在 i = 0 以及 i = 1 的时候是没有办法进⾏推导的,因
为 dp[-2] 或 dp[-1] 不是⼀个有效的数据。
因此我们需要在填表之前,将 0, 1, 2 位置的值初始化。题⽬中已经告诉我们 dp[0] = 0,
dp[1] = dp[2] = 1 。 - 填表顺序:
毫⽆疑问是「从左往右」。 - 返回值:
应该返回 dp[n] 的值。
3、代码实现
普通版
class Solution {
public:int tribonacci(int n) {if(n==0) return 0;if(n==1 || n==2) return 1;vector<int> dp(n+1);dp[0]=0,dp[1]=1,dp[2]=1;for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];}return dp[n];}
};
空间优化版
class Solution {
public:int tribonacci(int n) {if(n==0) return 0;if(n==1 || n==2) return 1;int a=0,b=1,c=1,d=0;for(int i=3;i<=n;i++){d=a+b+c;a=b;b=c;c=d;}return d;}
};
二、三步问题
1、题目讲解

2、思路讲解
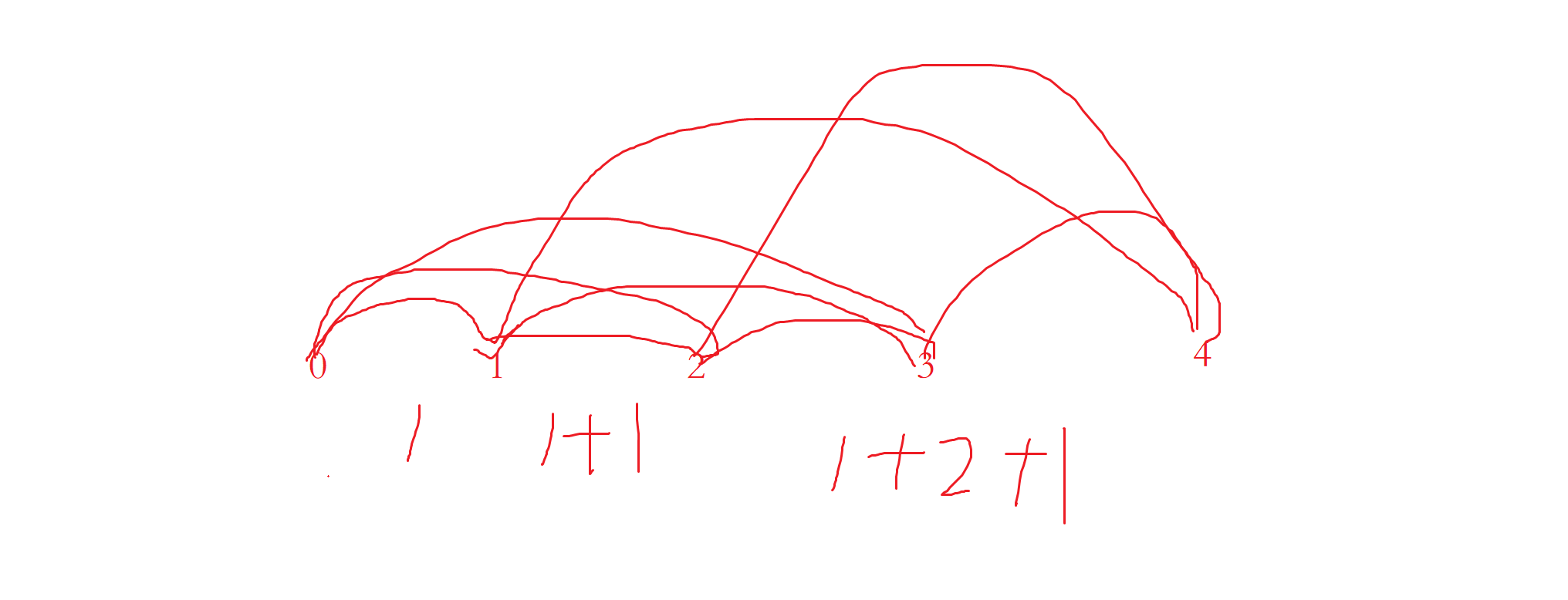
- 状态表⽰
这道题可以根据「经验 + 题⽬要求」直接定义出状态表⽰:
dp[i] 表⽰:到达 i 位置时,⼀共有多少种⽅法。 - 状态转移⽅程
以 i 位置状态的最近的⼀步,来分情况讨论:
如果 dp[i] 表⽰⼩孩上第 i 阶楼梯的所有⽅式,那么它应该等于所有上⼀步的⽅式之和:
i. 上⼀步上⼀级台阶, dp[i] += dp[i - 1] ;
ii. 上⼀步上两级台阶, dp[i] += dp[i - 2] ;
iii. 上⼀步上三级台阶, dp[i] += dp[i - 3] ;
综上所述, dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] 。
需要注意的是,这道题⽬说,由于结果可能很⼤,需要对结果取模。
在计算的时候,三个值全部加起来再取模,即 (dp[i - 1] + dp[i - 2] + dp[i - 3])
% MOD 是不可取的,同学们可以试验⼀下, n 取题⽬范围内最⼤值时,⽹站会报错 signed
integer overflow 。
对于这类需要取模的问题,我们每计算⼀次(两个数相加/乘等),都需要取⼀次模。否则,万⼀
发⽣了溢出,我们的答案就错了。 - 初始化
从我们的递推公式可以看出, dp[i] 在 i = 0, i = 1 以及 i = 2 的时候是没有办法进⾏
推导的,因为 dp[-3] dp[-2] 或 dp[-1] 不是⼀个有效的数据。
因此我们需要在填表之前,将 1, 2, 3 位置的值初始化。
根据题意, dp[1] = 1, dp[2] = 2, dp[3] = 4 。 - 填表顺序
毫⽆疑问是「从左往右」。 - 返回值
应该返回 dp[n] 的值。
3、代码实现
class Solution {
public:int waysToStep(int n) {if(n==1 || n==2) return n;if(n==3) return 4;const int MOD=1e9+7;vector<int> dp(n+1);dp[1]=1,dp[2]=2,dp[3]=4;for(int i=4;i<=n;i++){dp[i]= ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;}return dp[n];}
};
三、使用最小花费爬楼梯
1、题目讲解

2、思路讲解
方法一:
- 状态表⽰:
这道题可以根据「经验 + 题⽬要求」直接定义出状态表⽰:
第⼀种:以 i 位置为结尾,巴拉巴拉
dp[i] 表⽰:到达 i 位置时的最⼩花费。(注意:到达 i 位置的时候, i 位置的钱不需要
算上) - 状态转移⽅程:
根据最近的⼀步,分情况讨论:
▪ 先到达 i - 1 的位置,然后⽀付 cost[i - 1] ,接下来⾛⼀步⾛到 i 位置:
dp[i - 1] + csot[i - 1] ;
▪ 先到达 i - 2 的位置,然后⽀付 cost[i - 2] ,接下来⾛⼀步⾛到 i 位置:
dp[i - 2] + csot[i - 2] 。 - 初始化:
从我们的递推公式可以看出,我们需要先初始化 i = 0 ,以及 i = 1 位置的值。容易得到
dp[0] = dp[1] = 0 ,因为不需要任何花费,就可以直接站在第 0 层和第 1 层上。 - 填表顺序:
根据「状态转移⽅程」可得,遍历的顺序是「从左往右」。 - 返回值:
根据「状态表⽰以及题⽬要求」,需要返回 dp[n] 位置的值。
方法二:
- 状态表⽰:
这道题可以根据「经验 + 题⽬要求」直接定义出状态表⽰:
第⼆种:以 i 位置为起点,巴拉巴拉。
dp[i] 表⽰:从 i 位置出发,到达楼顶,此时的最⼩花费。 - 状态转移⽅程:
根据最近的⼀步,分情况讨论:
▪ ⽀付 cost[i] ,往后⾛⼀步,接下来从 i + 1 的位置出发到终点: dp[i + 1] +
cost[i] ;
▪ ⽀付 cost[i] ,往后⾛两步,接下来从 i + 2 的位置出发到终点: dp[i + 2] +
cost[i] ;
我们要的是最⼩花费,因此 dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i] 。 - 初始化:
为了保证填表的时候不越界,我们需要初始化最后两个位置的值,结合状态表⽰易得: dp[n -
1] = cost[n - 1], dp[n - 2] = cost[n - 2] - 填表顺序:
根据「状态转移⽅程」可得,遍历的顺序是「从右往左」。 - 返回值:
根据「状态表⽰以及题⽬要求」,需要返回 dp[n] 位置的值。
3、代码实现
方法一:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n+1);dp[0]=0,dp[1]=0;for(int i=2;i<=n;i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[n]; }
};
方法二:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n);dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];for(int i=n-3;i>=0;i--){dp[i]=cost[i]+min(dp[i+1],dp[i+2]);}return min(dp[0],dp[1]);}
};
四、解码方法
1、题目讲解

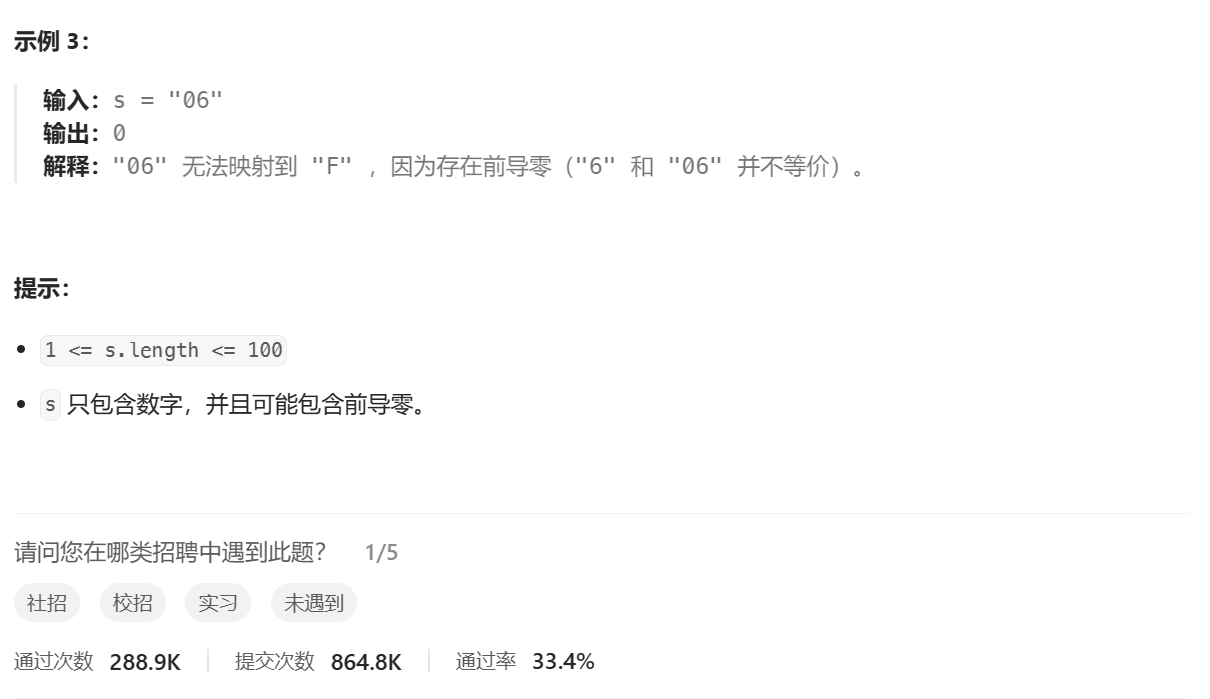
2、思路讲解
-
状态表⽰:
根据以往的经验,对于⼤多数线性 dp ,我们经验上都是「以某个位置结束或者开始」做⽂章,这
⾥我们继续尝试「⽤ i 位置为结尾」结合「题⽬要求」来定义状态表⽰。
dp[i] 表⽰:字符串中 [0,i] 区间上,⼀共有多少种编码⽅法。 -
状态转移⽅程:
定义好状态表⽰,我们就可以分析 i 位置的 dp 值,如何由「前⾯」或者「后⾯」的信息推导出
来。
关于 i 位置的编码状况,我们可以分为下⾯两种情况:
i. 让 i 位置上的数单独解码成⼀个字⺟;
ii. 让 i 位置上的数与 i - 1 位置上的数结合,解码成⼀个字⺟。下⾯我们就上⾯的两种解码情况,继续分析:
让 i 位置上的数单独解码成⼀个字⺟,就存在「解码成功」和「解码失败」两种情况:
i. 解码成功:当 i 位置上的数在 [1, 9] 之间的时候,说明 i 位置上的数是可以单独解
码的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 1] 区间上的解码⽅法。因为 [0, i - 1] 区间上的所有解码结果,后⾯填上⼀个 i 位置解码后的字⺟就可以了。此时 dp[i] = dp[i - 1] ;ii. 解码失败:当 i 位置上的数是 0 的时候,说明 i 位置上的数是不能单独解码的,那么
此时 [0, i] 区间上不存在解码⽅法。因为 i 位置如果单独参与解码,但是解码失败
了,那么前⾯做的努⼒就全部⽩费了。此时 dp[i] = 0 。
让 i 位置上的数与 i - 1 位置上的数结合在⼀起,解码成⼀个字⺟,也存在「解码成功」和「解码失败」两种情况:
i. 解码成功:当结合的数在 [10, 26] 之间的时候,说明 [i - 1, i] 两个位置是可以
解码成功的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 2 ] 区间上的解码
⽅法,原因同上。此时 dp[i] = dp[i - 2] ;
ii. 解码失败:当结合的数在 [0, 9] 和 [27 , 99] 之间的时候,说明两个位置结合后解码失败(这⾥⼀定要注意 00 01 02 03 04 … 这⼏种情况),那么此时 [0, i] 区间上的解码⽅法就不存在了,原因依旧同上。此时 dp[i] = 0 。综上所述: dp[i] 最终的结果应该是上⾯四种情况下,解码成功的两种的累加和(因为我们关⼼
的是解码⽅法,既然解码失败,就不⽤加⼊到最终结果中去),因此可以得到状态转移⽅程
( dp[i] 默认初始化为 0 ):
i. 当 s[i] 上的数在 [1, 9] 区间上时: dp[i] += dp[i - 1] ;
ii. 当 s[i - 1] 与 s[i] 上的数结合后,在 [10, 26] 之间的时候: dp[i] +=
dp[i - 2] ;
如果上述两个判断都不成⽴,说明没有解码⽅法, dp[i] 就是默认值 0 。
3、代码实现
优化前:
class Solution {
public:int numDecodings(string s) {int n=s.size();vector<int> dp(n);dp[0]=s[0]!='0';if(n==1) return dp[0];if(s[1]!='0' && s[0]!='0') dp[1]++;int t=(s[0]-'0')*10+(s[1]-'0');if(t>=10 && t<=26) dp[1]++;for(int i=2;i<n;i++){if(s[i]!='0') dp[i]+=dp[i-1];int t=(s[i-1]-'0')*10+(s[i]-'0');if(t>=10 && t<=26) dp[i]+=dp[i-2];}return dp[n-1];}
};优化后:
class Solution {
public:int n=s.size();vector<int> dp(n+1);dp[0]=1;dp[1]=s[1-1]!='0';for(int i=2;i<=n;i++){if(s[i-1]!='0') dp[i]+=dp[i-1];int t=(s[i-2]-'0')*10+(s[i-1]-'0');if(t>=10 && t<=26) dp[i]+=dp[i-2];}return dp[n];}
};
相关文章:

动态规划——OJ题(一)
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、第N个泰波那契数1、题目讲解2、思路讲解3、代码实现 二、三步问题1、题目讲解2、思路讲解…...
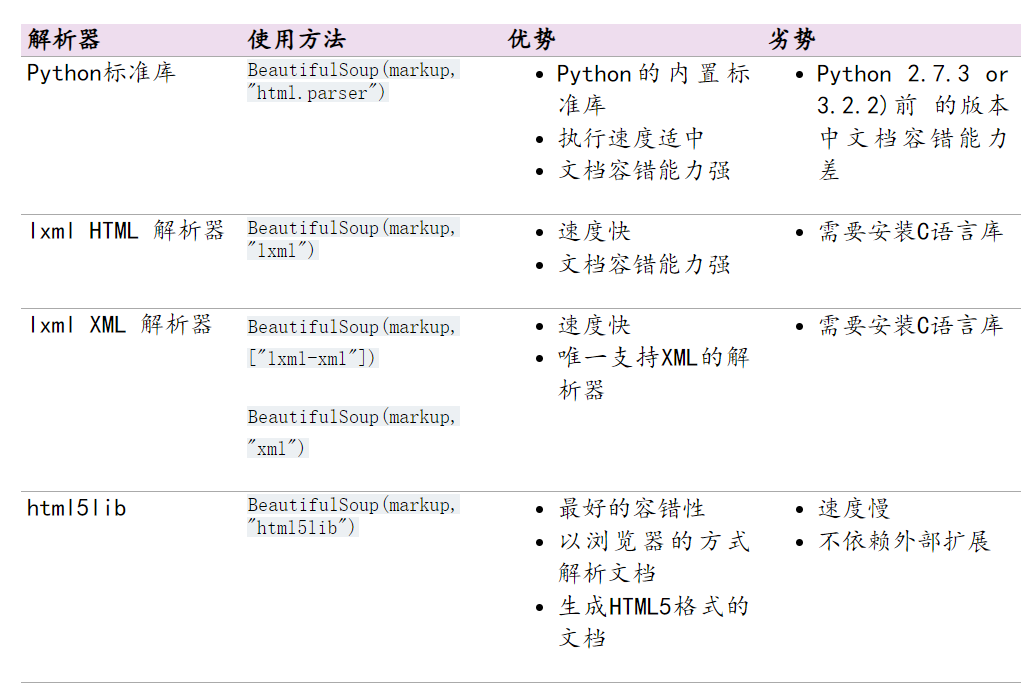
六:爬虫-数据解析之BeautifulSoup4
六:bs4简介 基本概念: 简单来说,Beautiful Soup是python的一个库,最主要的功能是从网页抓取数据官方解释如下: Beautiful Soup提供一些简单的、python式的函数用来处理导航、搜索、修改分析树等功能。 它是一个工具箱…...

音频筑基:总谐波失真THD+N指标
音频筑基:总谐波失真THDN指标 THDN含义深入理解 在分析音频信号中,THDN指标是我们经常遇到的概念,这里谈谈自己的理解。 THDN含义 首先,理解THD的定义: THD,Total Harmonic Distortion,总谐波…...
自动驾驶技术:驶向未来的智能之路
导言 自动驾驶技术正引领着汽车产业向着更安全、高效、智能的未来演进。本文将深入研究自动驾驶技术的核心原理、关键技术、应用场景以及对交通、社会的深远影响。 1. 简介 自动驾驶技术是基于先进传感器、计算机视觉、机器学习等技术的创新,旨在实现汽车在不需要人…...

TIGRE: a MATLAB-GPU toolbox for CBCT image reconstruction
TIGRE: 用于CBCT图像重建的MATLAB-GPU工具箱 论文链接:https://iopscience.iop.org/article/10.1088/2057-1976/2/5/055010 项目链接:https://github.com/CERN/TIGRE Abstract 本文介绍了基于层析迭代GPU的重建(TIGRE)工具箱,这是一个用于…...

我的NPI项目之Android 安全系列 -- EMVCo
最近一直在和支付有关的内容纠缠,原来我负责的产品后面还要过EMVCo的认证。于是,就网上到处找找啥事EMVCo,啥是EMVCo,啥是EMVCo。 于是找到了一个神奇的个人网站:Ganeshji Marwaha 虽然时间有点久远,但是用…...
vue中实现使用相框点击拍照,canvas进行前端图片合并下载
拍照和相框合成,下载图片dome 一、canvas介绍 Canvas是一个HTML5元素,它提供了一个用于在网页上绘制图形、图像和动画的2D渲染上下文。Canvas可以用于创建各种图形,如线条、矩形、圆形、文本等,并且可以通过JavaScript进行编程操作。 Canvas元素本身是一个矩形框,可以通…...

边缘检测@获取labelme标注的json黑白图掩码mask
import cv2 as cv import numpy as np import json import os from PIL import Imagedef convertPolygonToMask(jsonfilePath):...

嵌入式培训-数据结构-day23-线性表
线性表 线性表是包含若干数据元素的一个线性序列 记为: L(a0, ...... ai-1, ai, ai1 ...... an-1) L为表名,ai (0≤i≤n-1)为数据元素; n为表长,n>0 时,线性表L为非空表,否则为空表。 线性表L可用二元组形式描述…...
C# DotNetCore AOP简单实现
背景 实际开发中业务和日志尽量不要相互干扰嵌套,否则很难维护和调试。 示例 using System.Reflection;namespace CSharpLearn {internal class Program{static void Main(){int age 25;string name "bingling";Person person new(age, name);Conso…...

19.Tomcat搭建
Tomcat 简介 Tomcat的安装和启动 前置条件 • JDK 已安装(JAVA_HOME环境变量已被成功配置) Windows 下安装 访问 http://tomcat.apache.org ⇒ 左侧边栏 “Download” 2. 解压缩下载的文件到 “D:\tomcat”, tomcat的内容最终被解压到 “D:\tomcat\apache-tomcat-9.0.84” 3.…...

HarmonyOS云开发基础认证考试满分答案(100分)【全网最全-不断更新】【鸿蒙专栏-29】
系列文章: HarmonyOS应用开发者基础认证满分答案(100分) HarmonyOS应用开发者基础认证【闯关习题 满分答案】 HarmonyOS应用开发者高级认证满分答案(100分) HarmonyOS云开发基础认证满分答案(100分…...

Unity项目里Log系统该怎么设计
其实并没有想完整就设计一个好用的Log系统,然后发出来。记录这个的原因,是在书里看到这么一句话,Log会消耗资源,特别是写文件,因此可以设置一个Log缓冲区,等缓冲区满了再一次性写入文件,以节省资…...

设计模式-状态(State)模式
目录 开发过程中的一些场景 状态模式的简单介绍 状态模式UML类图 类图讲解 适用场景 Java中的例子 案例讲解 什么是状态机 如何实现状态机 SpringBoot状态自动机 优点 缺点 与其他模式的区别 小结 开发过程中的一些场景 我们在平时的开发过程中,经常会…...

oracle怎么存放json好
Oracle数据库提供了多种方式来存储JSON数据。你可以将JSON数据存储在VARCHAR2、CLOB或BLOB数据类型中,或者使用Oracle提供的JSON数据类型。 如果你选择使用VARCHAR2数据类型来存储JSON数据,你可以直接将JSON字符串存储在其中。例如: CREATE…...

【计算机网络】—— 详解码元,传输速率的计算|网络奇缘系列|计算机网络
🌈个人主页: Aileen_0v0🔥系列专栏: 一见倾心,再见倾城 --- 计算机网络~💫个人格言:"没有罗马,那就自己创造罗马~" 目录 码元 速率和波特 思考1 思考2 思考3 带宽(Bandwidth) 📝总结 码元…...
[ 云计算 | Azure 实践 ] 在 Azure 门户中创建 VM 虚拟机并进行验证
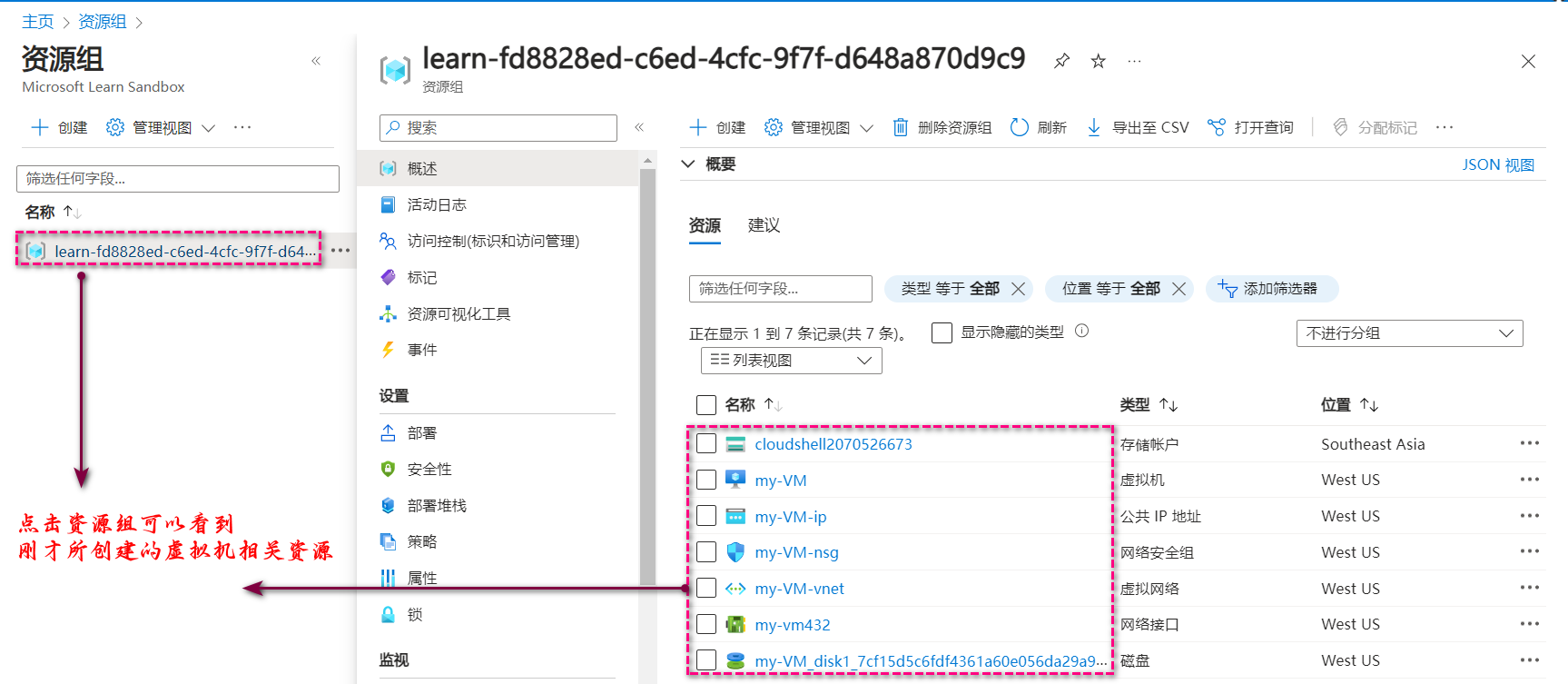
文章目录 一、前言二、在 Azure Portal 中创建 VM三、验证已创建的虚拟机资源3.1 方法一:在虚拟机服务中查看验证3.1 方法二:在资源组服务中查看验证 四、文末总结 一、前言 本文会开始创建新系列的专栏,专门更新 Azure 云实践相关的文章。 …...
计算机网络:网络层(无分类编址CIDR、计算题讲解)
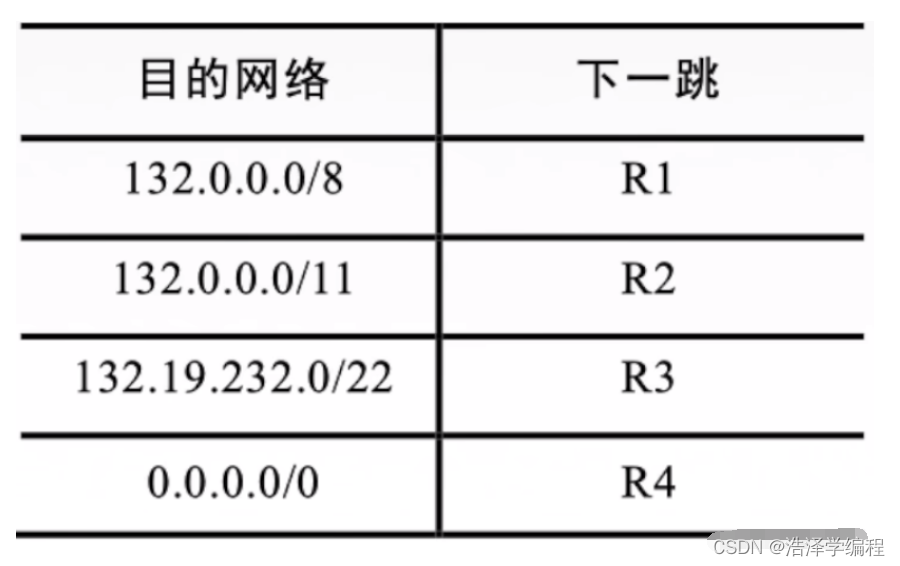
带你快速通关期末 文章目录 前言一、无分类编址CIDR简介二、构成超网三、最长前缀匹配总结 前言 我们在前面知道了分类地址,但是分类地址又有很多缺陷: B类地址很快将分配完毕!路由表中的项目急剧增长! 一、无分类编址CIDR简介 无分类域间路由选择CI…...

Learning Semantic-Aware Knowledge Guidance forLow-Light Image Enhancement
微光图像增强(LLIE)研究如何提高照明并生成正常光图像。现有的大多数方法都是通过全局和统一的方式来改善低光图像,而不考虑不同区域的语义信息。如果没有语义先验,网络可能很容易偏离区域的原始颜色。为了解决这个问题࿰…...

关于嵌入式开发的一些信息汇总:开发模型以及自托管开发(二)
关于嵌入式开发的一些信息汇总:开发模型及自托管开发(二) 2 自托管开发2.2 构建 Raspberry Pi 内核2.3 安装内核2.4 总结 3 连接目标板3.1 Raspberry Pi 上的网络设置3.2 Ssh、rsh、rlogin 和 telnet 连接到目标 4 应用程序开发4.1 在目标板上…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
