深度学习中的13种概率分布
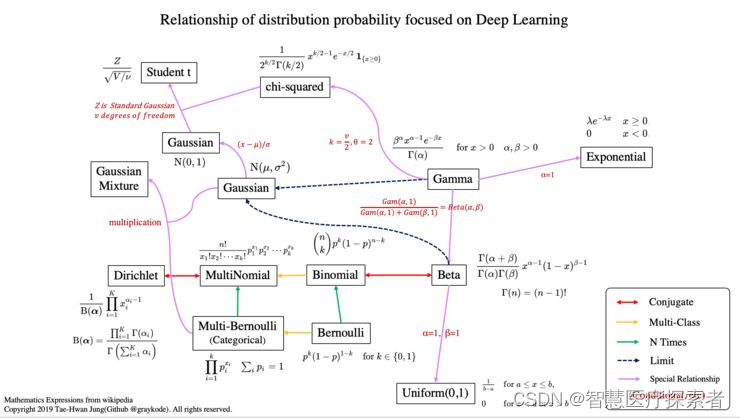
1 概率分布概述
-
共轭意味着它有共轭分布的关系。
在贝叶斯概率论中,如果后验分布 p(θx)与先验概率分布 p(θ)在同一概率分布族中,则先验和后验称为共轭分布,先验称为似然函数的共轭先验。
-
多分类表示随机方差大于 2。
-
n 次意味着我们也考虑了先验概率 p(x)。
2 分布概率与特征
2.1 均匀分布(连续)
均匀分布在 [a,b] 上具有相同的概率值,是简单概率分布。
示例代码:
import numpy as np
from matplotlib import pyplot as pltdef uniform(x, a, b):y = [1 / (b - a) if a <= val and val <= belse 0 for val in x]return x, y, np.mean(y), np.std(y)x = np.arange(-100, 100) # define range of x
for ls in [(-50, 50), (10, 20)]:a, b = ls[0], ls[1]x, y, u, s = uniform(x, a, b)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))plt.legend()
plt.show()运行代码显示:
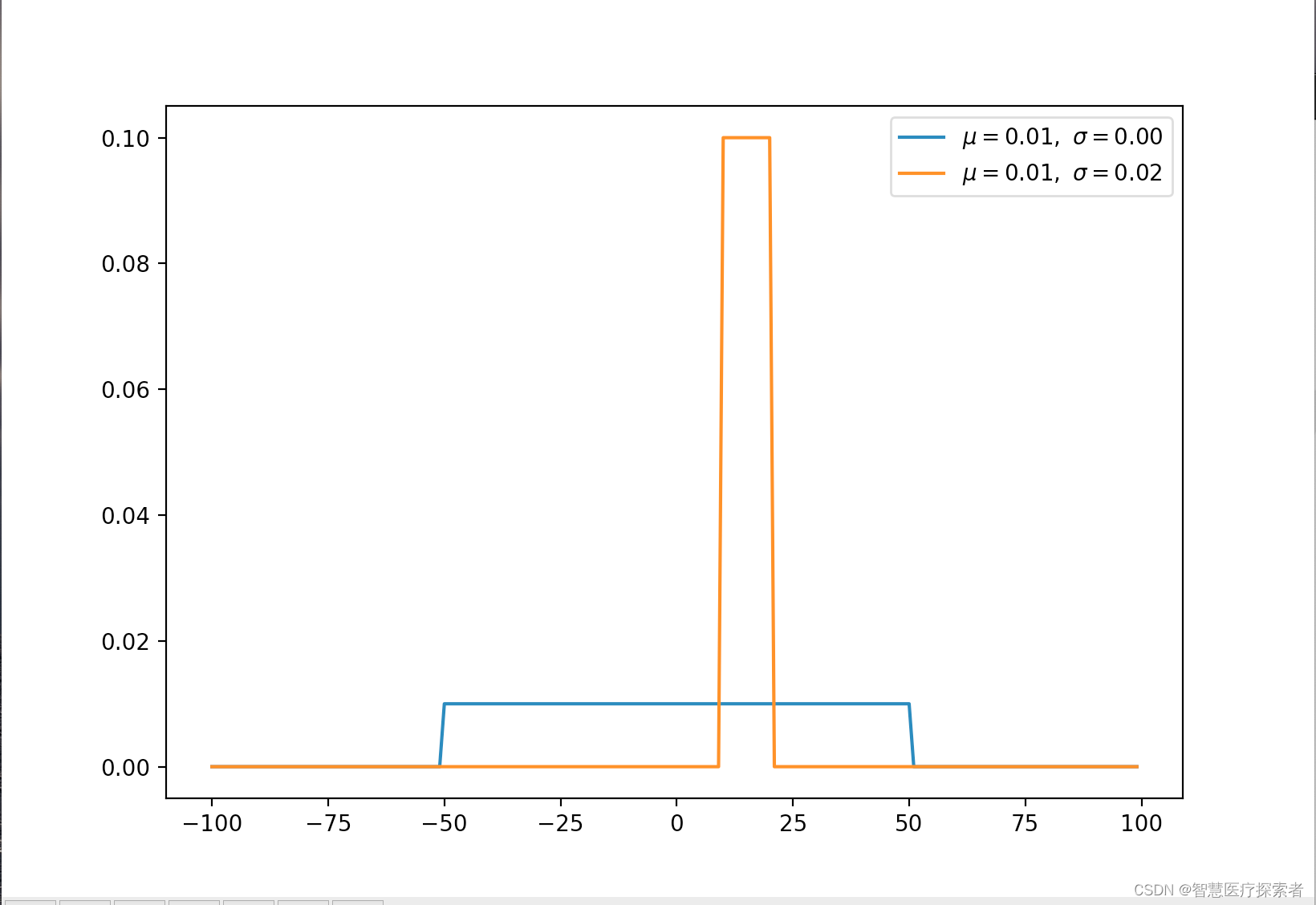
2.2 伯努利分布(离散)
-
先验概率 p(x)不考虑伯努利分布。因此,如果我们对最大似然进行优化,那么我们很容易被过度拟合。
-
利用二元交叉熵对二项分类进行分类。它的形式与伯努利分布的负对数相同。
示例代码:
import random
import numpy as np
from matplotlib import pyplot as pltdef bernoulli(p, k):return p if k else 1 - pn_experiment = 100
p = 0.6
x = np.arange(n_experiment)
y = []
for _ in range(n_experiment):pick = bernoulli(p, k=bool(random.getrandbits(1)))y.append(pick)u, s = np.mean(y), np.std(y)
plt.scatter(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))
plt.legend()
plt.show()运行代码显示:
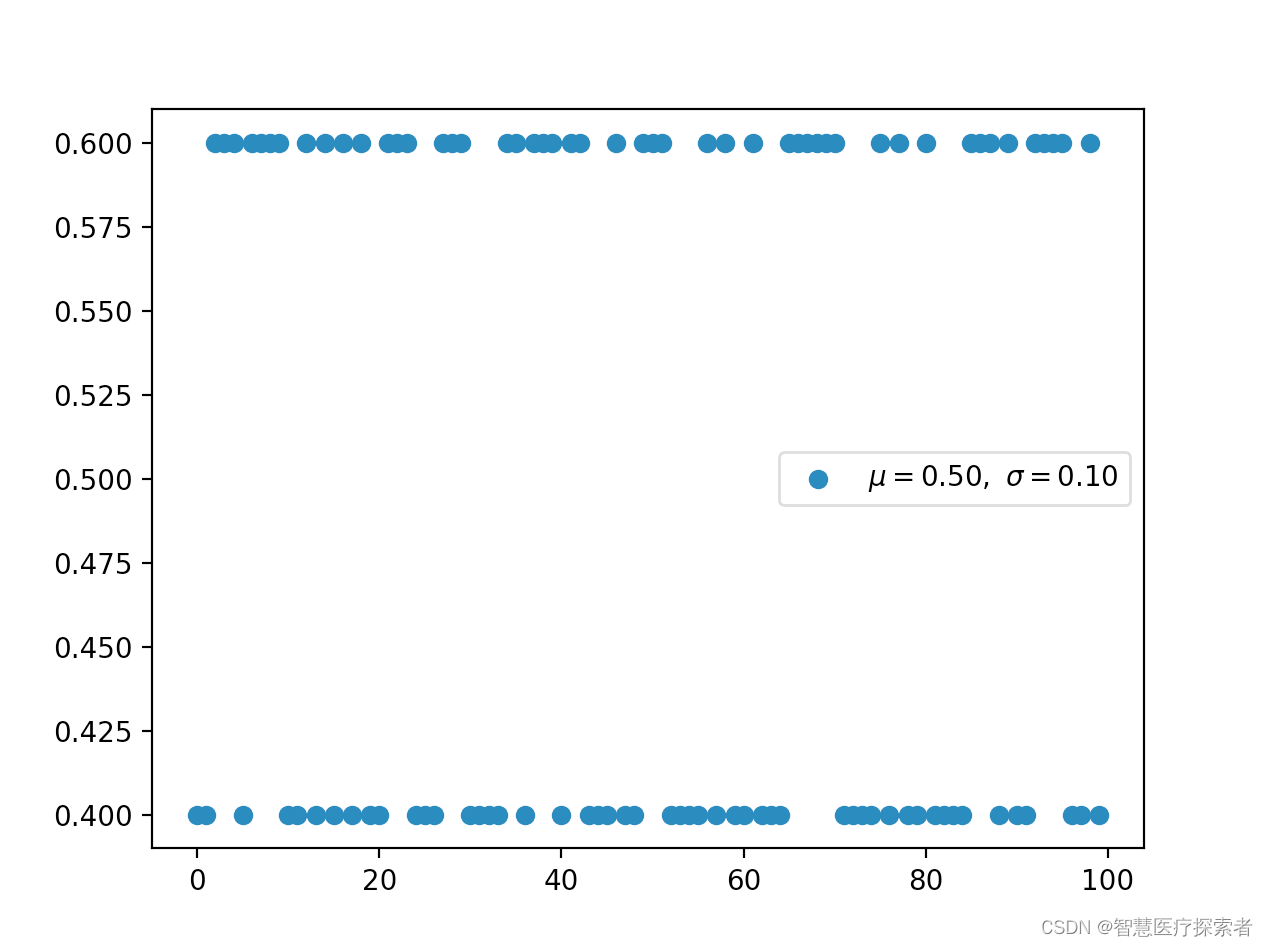
2.3 二项分布(离散)
-
参数为 n 和 p 的二项分布是一系列 n 个独立实验中成功次数的离散概率分布。
-
二项式分布是指通过指定要提前挑选的数量而考虑先验概率的分布。
示例代码:
import numpy as np
from matplotlib import pyplot as pltimport operator as op
from functools import reducedef const(n, r):r = min(r, n-r)numer = reduce(op.mul, range(n, n-r, -1), 1)denom = reduce(op.mul, range(1, r+1), 1)return numer / denomdef binomial(n, p):q = 1 - py = [const(n, k) * (p ** k) * (q ** (n-k)) for k in range(n)]return y, np.mean(y), np.std(y)for ls in [(0.5, 20), (0.7, 40), (0.5, 40)]:p, n_experiment = ls[0], ls[1]x = np.arange(n_experiment)y, u, s = binomial(n_experiment, p)plt.scatter(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))plt.legend()
plt.show()运行代码显示:
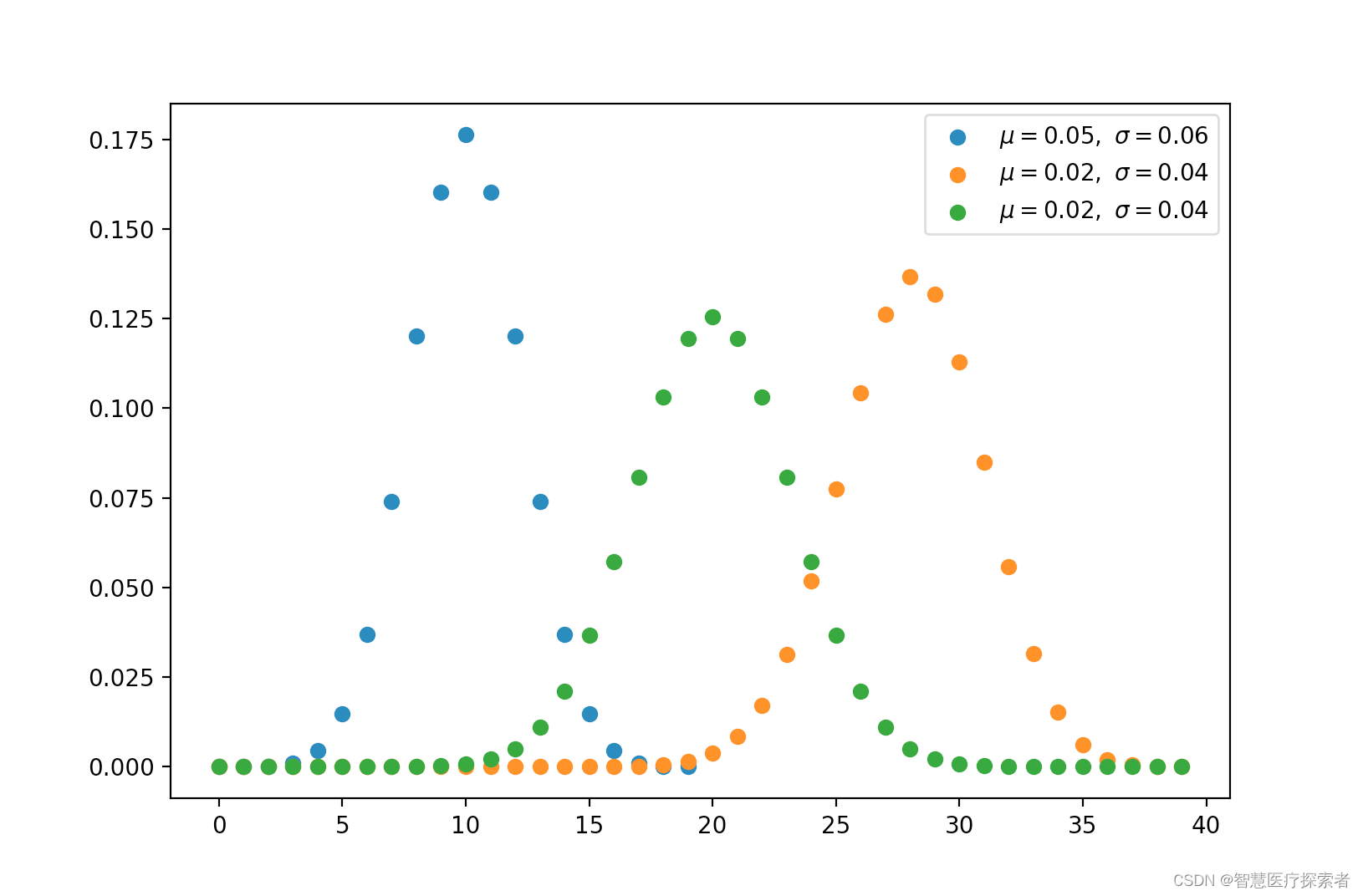
2.4 多伯努利分布,分类分布(离散)
-
多伯努利称为分类分布。
-
交叉熵和采取负对数的多伯努利分布具有相同的形式。
示例代码:
import random
import numpy as np
from matplotlib import pyplot as pltdef categorical(p, k):return p[k]n_experiment = 100
p = [0.2, 0.1, 0.7]
x = np.arange(n_experiment)
y = []
for _ in range(n_experiment):pick = categorical(p, k=random.randint(0, len(p) - 1))y.append(pick)u, s = np.mean(y), np.std(y)
plt.scatter(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))
plt.legend()
plt.show()运行代码显示:
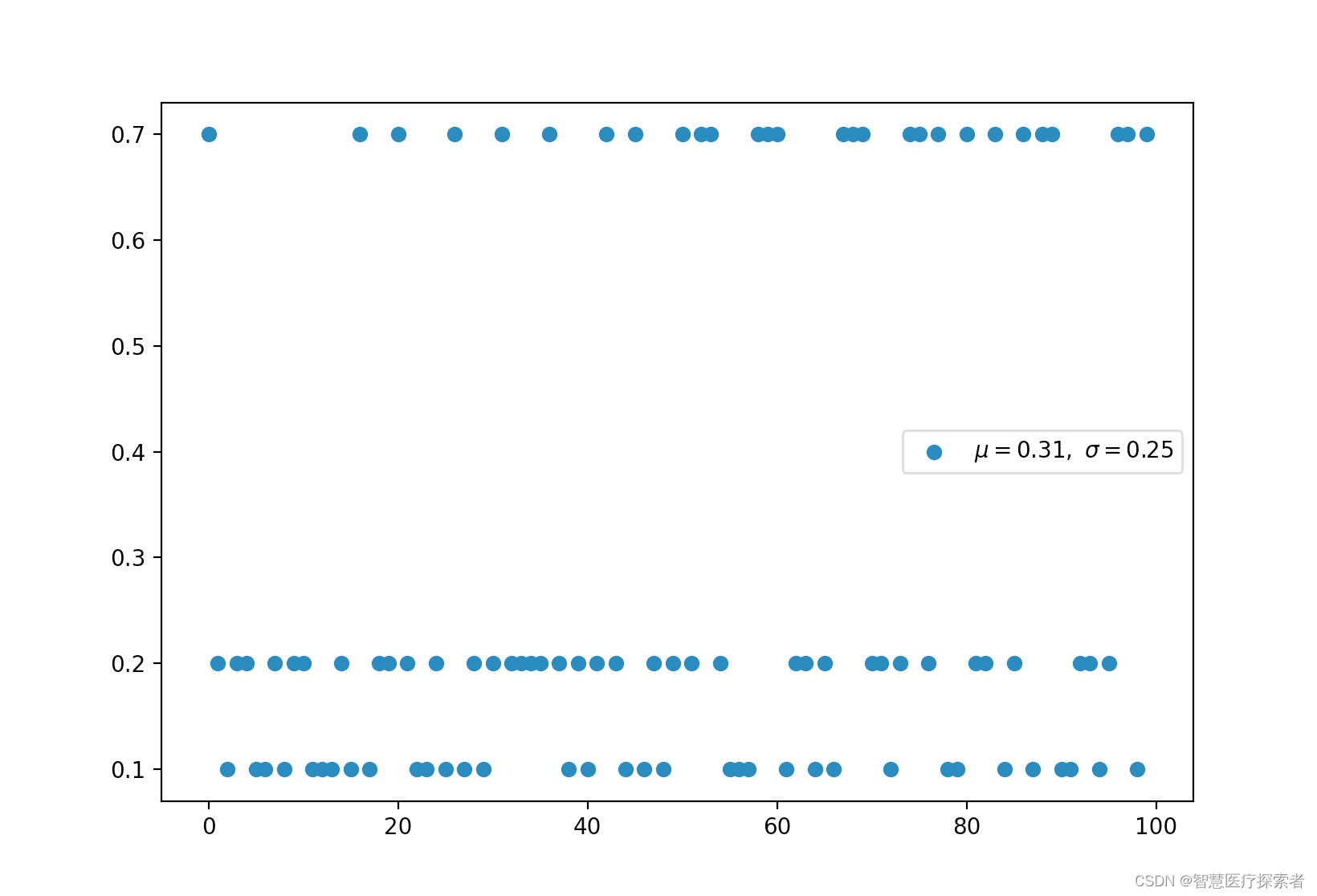
2.5 多项式分布(离散)
多项式分布与分类分布的关系与伯努尔分布与二项分布的关系相同。
示例代码:
import numpy as np
from matplotlib import pyplot as pltimport operator as op
from functools import reducedef factorial(n):return reduce(op.mul, range(1, n + 1), 1)def const(n, a, b, c):"""return n! / a! b! c!, where a+b+c == n"""assert a + b + c == nnumer = factorial(n)denom = factorial(a) * factorial(b) * factorial(c)return numer / denomdef multinomial(n):""":param x : list, sum(x) should be `n`:param n : number of trial:param p: list, sum(p) should be `1`"""# get all a,b,c where a+b+c == n, a<b<cls = []for i in range(1, n + 1):for j in range(i, n + 1):for k in range(j, n + 1):if i + j + k == n:ls.append([i, j, k])y = [const(n, l[0], l[1], l[2]) for l in ls]x = np.arange(len(y))return x, y, np.mean(y), np.std(y)for n_experiment in [20, 21, 22]:x, y, u, s = multinomial(n_experiment)plt.scatter(x, y, label=r'$trial=%d$' % (n_experiment))plt.legend()
plt.show()运行代码显示:
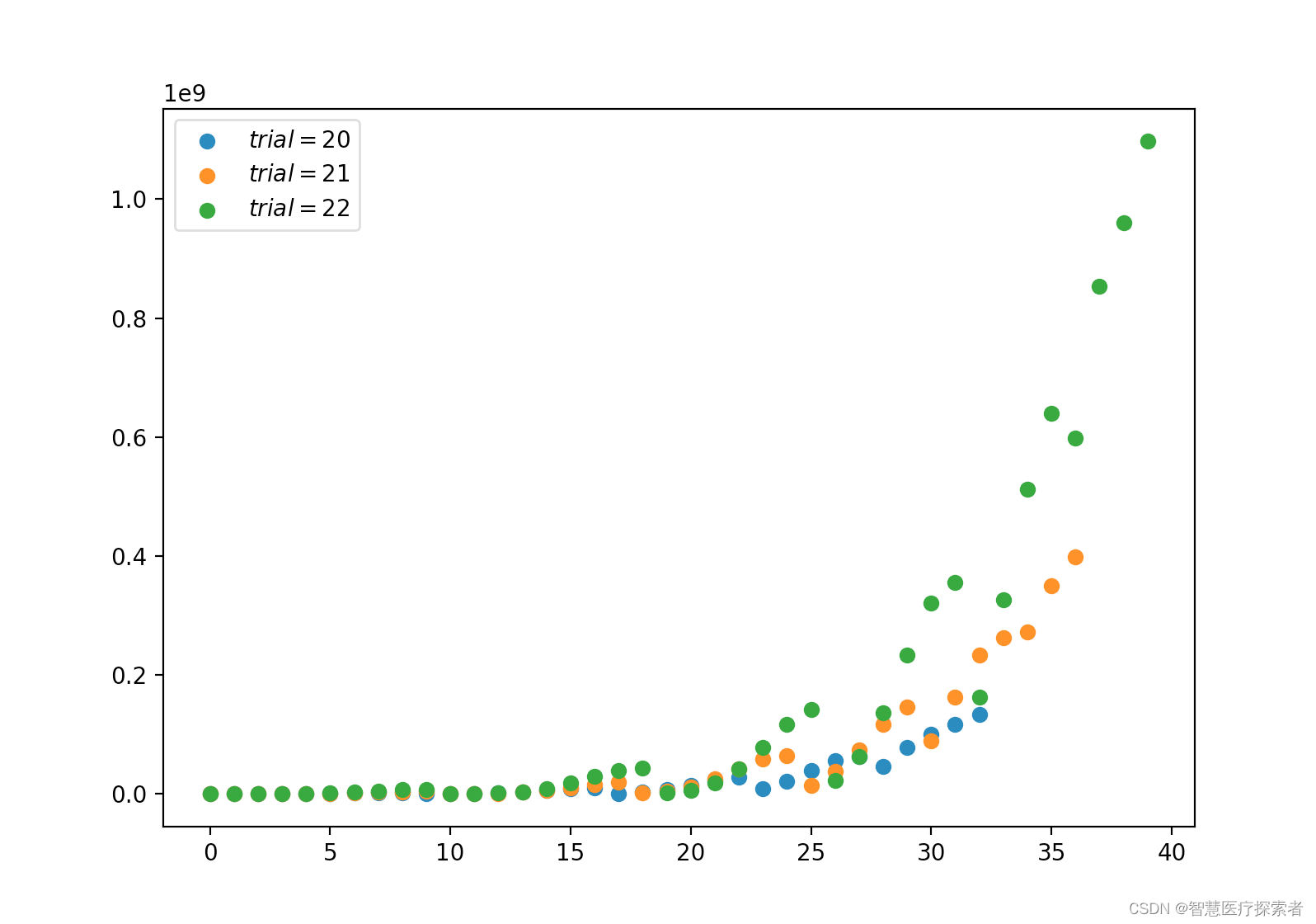
2.6 β分布(连续)
-
β分布与二项分布和伯努利分布共轭。
-
利用共轭,利用已知的先验分布可以更容易地得到后验分布。
-
当β分布满足特殊情况(α=1,β=1)时,均匀分布是相同的。
示例代码:
import numpy as np
from matplotlib import pyplot as pltdef gamma_function(n):cal = 1for i in range(2, n):cal *= ireturn caldef beta(x, a, b):gamma = gamma_function(a + b) / \(gamma_function(a) * gamma_function(b))y = gamma * (x ** (a - 1)) * ((1 - x) ** (b - 1))return x, y, np.mean(y), np.std(y)for ls in [(1, 3), (5, 1), (2, 2), (2, 5)]:a, b = ls[0], ls[1]# x in [0, 1], trial is 1/0.001 = 1000x = np.arange(0, 1, 0.001, dtype=np.float)x, y, u, s = beta(x, a=a, b=b)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f,'r'\ \alpha=%d,\ \beta=%d$' % (u, s, a, b))
plt.legend()
plt.show()运行代码显示:
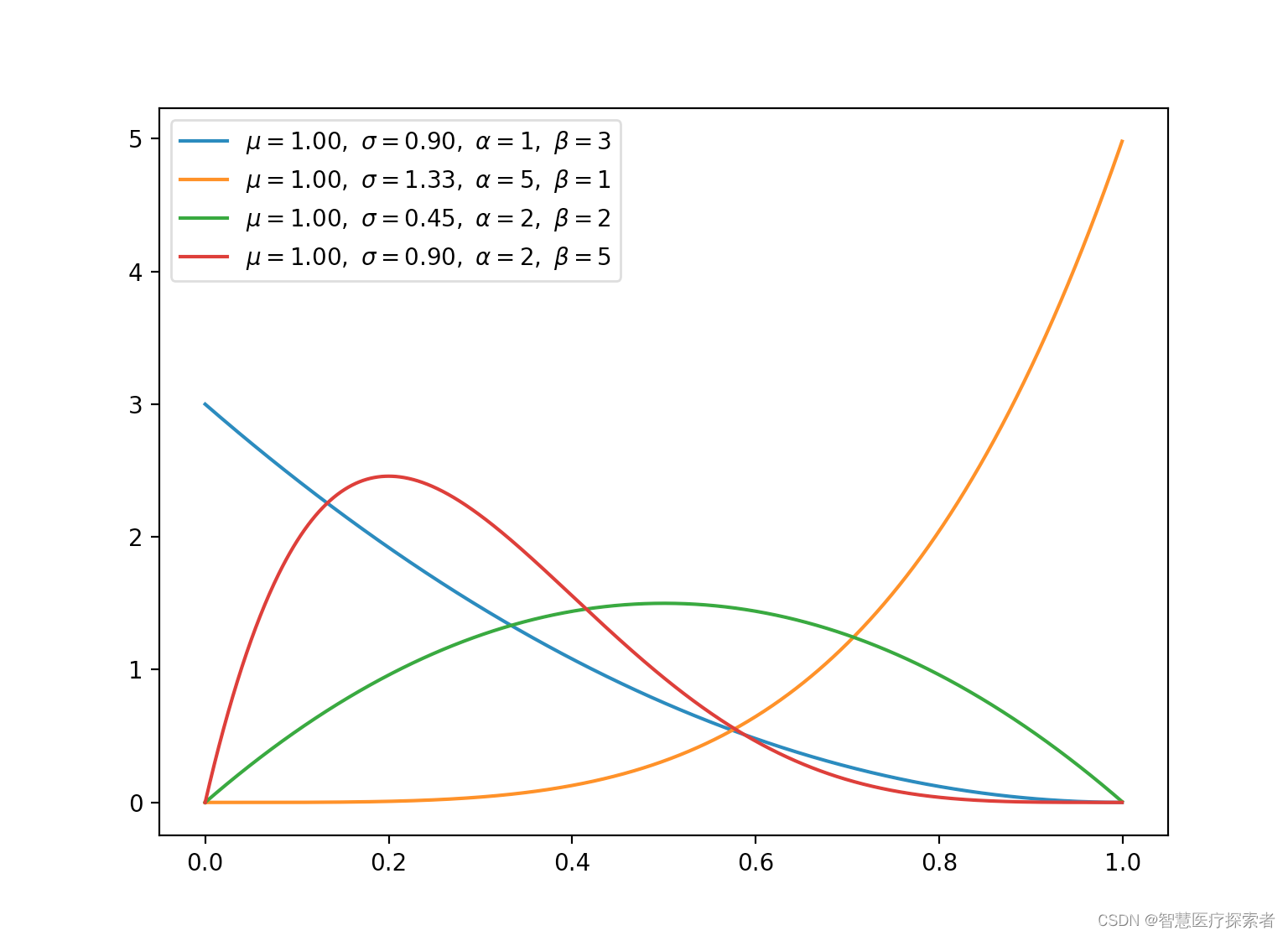
2.7 Dirichlet 分布(连续)
-
dirichlet 分布与多项式分布是共轭的。
-
如果 k=2,则为β分布。
示例代码:
from random import randint
import numpy as np
from matplotlib import pyplot as pltdef normalization(x, s):""":return: normalizated list, where sum(x) == s"""return [(i * s) / sum(x) for i in x]def sampling():return normalization([randint(1, 100),randint(1, 100), randint(1, 100)], s=1)def gamma_function(n):cal = 1for i in range(2, n):cal *= ireturn caldef beta_function(alpha):""":param alpha: list, len(alpha) is k:return:"""numerator = 1for a in alpha:numerator *= gamma_function(a)denominator = gamma_function(sum(alpha))return numerator / denominatordef dirichlet(x, a, n):""":param x: list of [x[1,...,K], x[1,...,K], ...], shape is (n_trial, K):param a: list of coefficient, a_i > 0:param n: number of trial:return:"""c = (1 / beta_function(a))y = [c * (xn[0] ** (a[0] - 1)) * (xn[1] ** (a[1] - 1))* (xn[2] ** (a[2] - 1)) for xn in x]x = np.arange(n)return x, y, np.mean(y), np.std(y)n_experiment = 1200
for ls in [(6, 2, 2), (3, 7, 5), (6, 2, 6), (2, 3, 4)]:alpha = list(ls)# random samping [x[1,...,K], x[1,...,K], ...], shape is (n_trial, K)# each sum of row should be one.x = [sampling() for _ in range(1, n_experiment + 1)]x, y, u, s = dirichlet(x, alpha, n=n_experiment)plt.plot(x, y, label=r'$\alpha=(%d,%d,%d)$' % (ls[0], ls[1], ls[2]))plt.legend()
plt.show()运行代码显示:
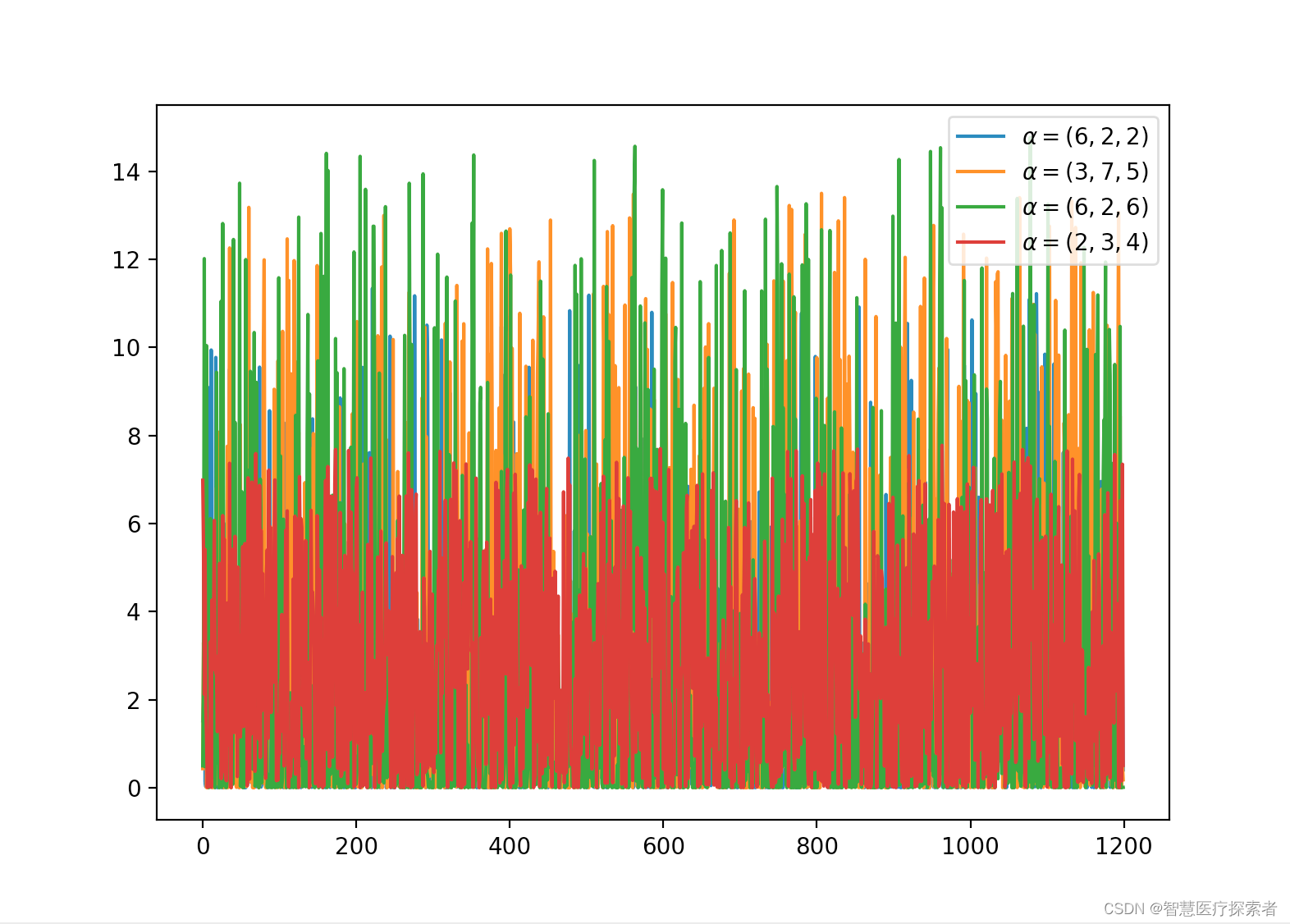
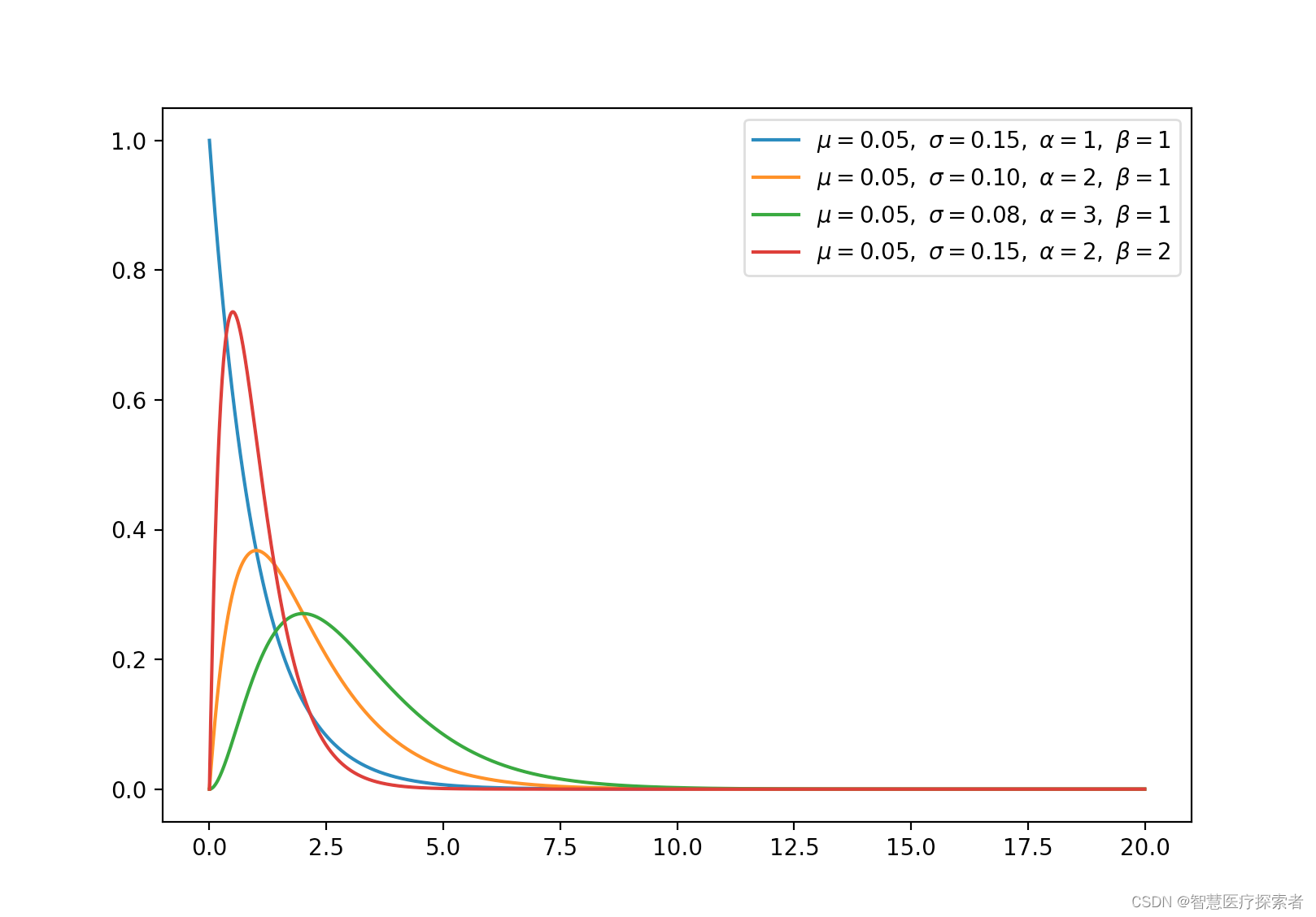
2.8 伽马分布(连续)
-
如果 gamma(a,1)/gamma(a,1)+gamma(b,1)与 beta(a,b)相同,则 gamma 分布为β分布。
-
指数分布和卡方分布是伽马分布的特例。
代码示例:
import numpy as np
from matplotlib import pyplot as pltdef gamma_function(n):cal = 1for i in range(2, n):cal *= ireturn caldef gamma(x, a, b):c = (b ** a) / gamma_function(a)y = c * (x ** (a - 1)) * np.exp(-b * x)return x, y, np.mean(y), np.std(y)for ls in [(1, 1), (2, 1), (3, 1), (2, 2)]:a, b = ls[0], ls[1]x = np.arange(0, 20, 0.01, dtype=np.float)x, y, u, s = gamma(x, a=a, b=b)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f,'r'\ \alpha=%d,\ \beta=%d$' % (u, s, a, b))
plt.legend()
plt.show()运行代码显示:
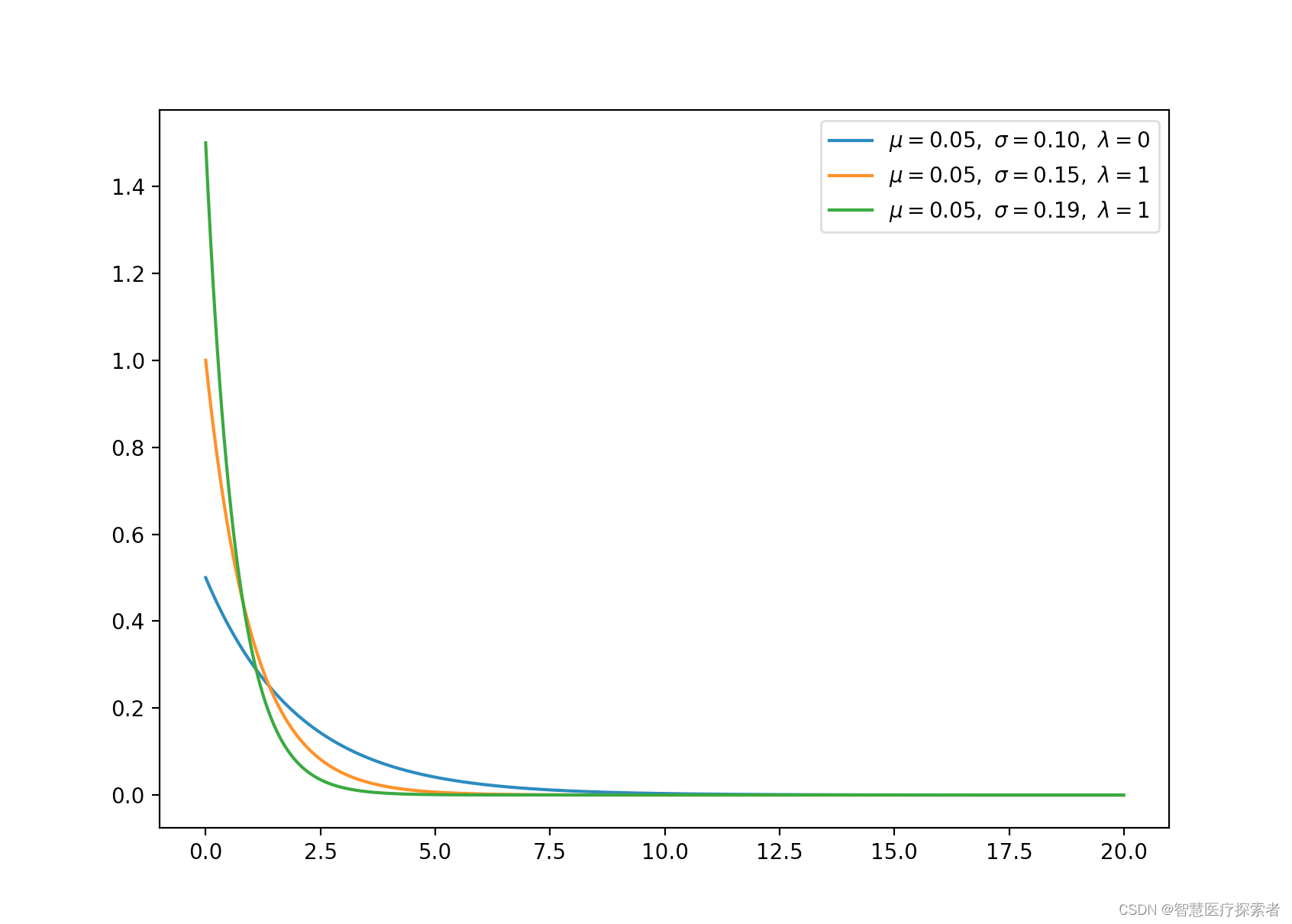
2.9 指数分布(连续)
指数分布是 α 为 1 时 γ 分布的特例。
import numpy as np
from matplotlib import pyplot as pltdef exponential(x, lamb):y = lamb * np.exp(-lamb * x)return x, y, np.mean(y), np.std(y)for lamb in [0.5, 1, 1.5]:x = np.arange(0, 20, 0.01, dtype=np.float)x, y, u, s = exponential(x, lamb=lamb)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f,'r'\ \lambda=%d$' % (u, s, lamb))
plt.legend()
plt.show()运行代码显示
2.10 高斯分布(连续)
高斯分布是一种非常常见的连续概率分布。
示例代码:
import numpy as np
from matplotlib import pyplot as pltdef gaussian(x, n):u = x.mean()s = x.std()# divide [x.min(), x.max()] by nx = np.linspace(x.min(), x.max(), n)a = ((x - u) ** 2) / (2 * (s ** 2))y = 1 / (s * np.sqrt(2 * np.pi)) * np.exp(-a)return x, y, x.mean(), x.std()x = np.arange(-100, 100) # define range of x
x, y, u, s = gaussian(x, 10000)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))
plt.legend()
plt.show()运行代码显示:

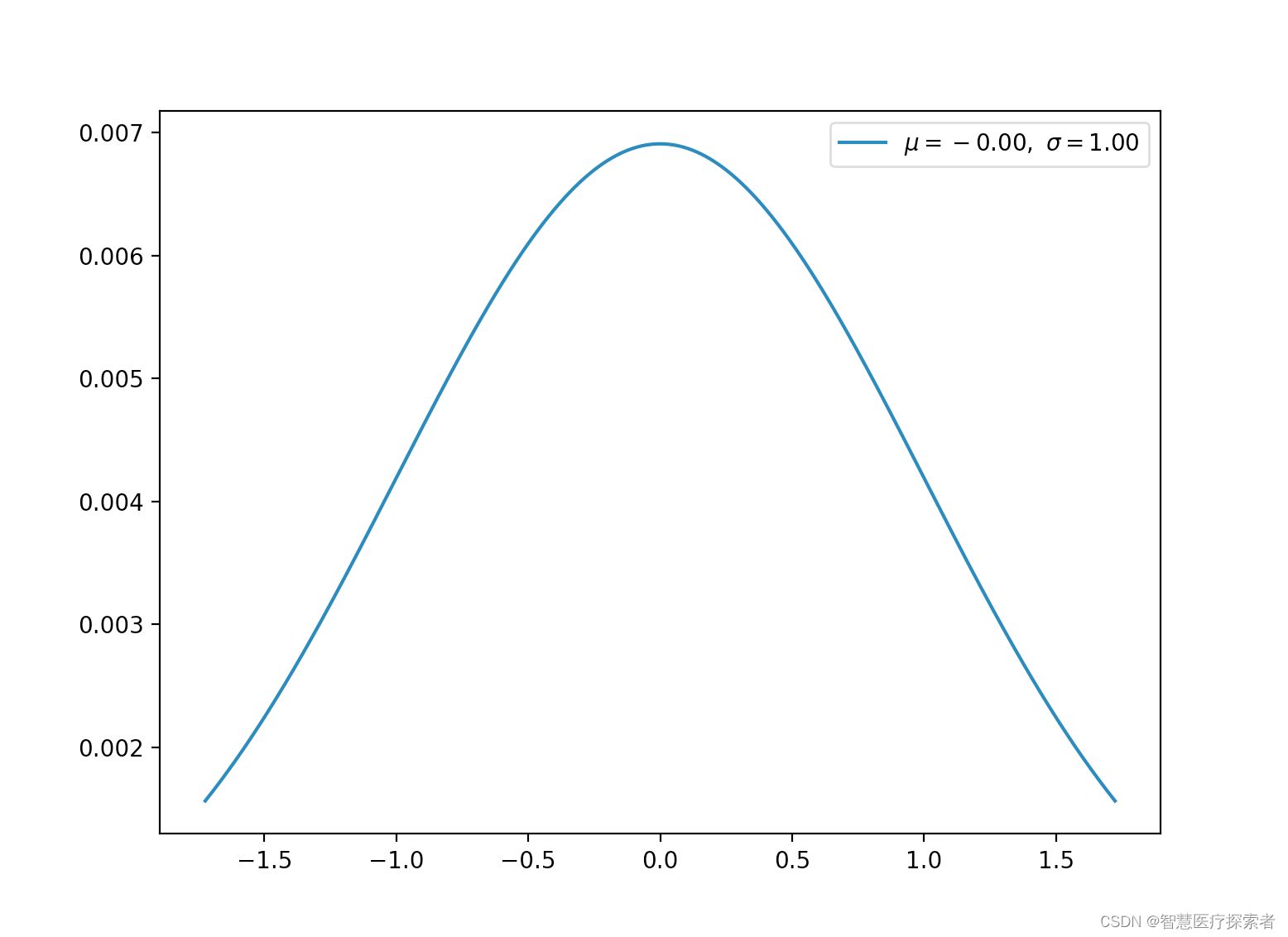
2.11 标准正态分布(连续)
标准正态分布为特殊的高斯分布,平均值为 0,标准差为 1。
import numpy as np
from matplotlib import pyplot as pltdef normal(x, n):u = x.mean()s = x.std()# normalizationx = (x - u) / s# divide [x.min(), x.max()] by nx = np.linspace(x.min(), x.max(), n)a = ((x - 0) ** 2) / (2 * (1 ** 2))y = 1 / (s * np.sqrt(2 * np.pi)) * np.exp(-a)return x, y, x.mean(), x.std()x = np.arange(-100, 100) # define range of x
x, y, u, s = normal(x, 10000)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))
plt.legend()
plt.show()运行代码显示:
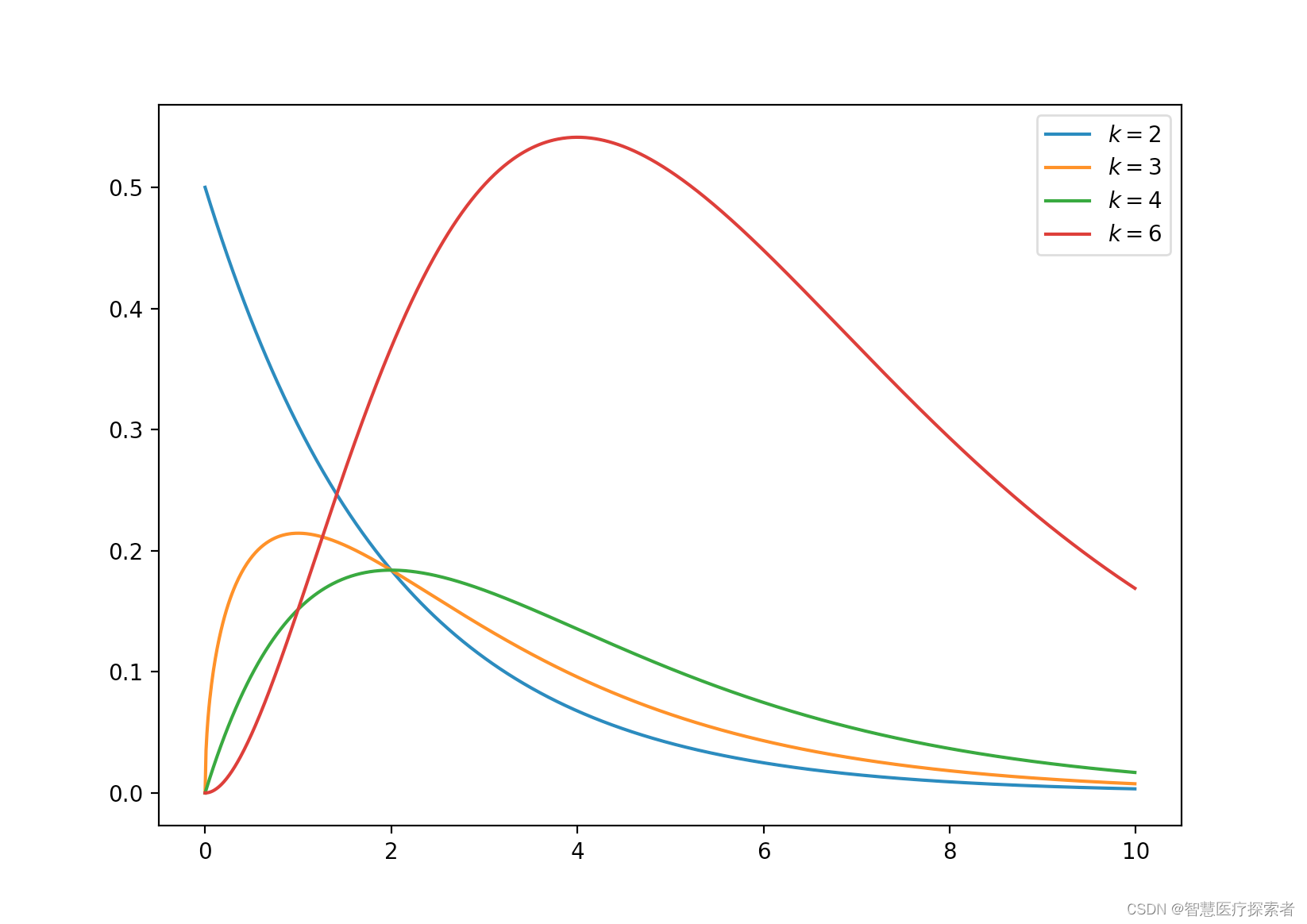
2.12 卡方分布(连续)
-
k 自由度的卡方分布是 k 个独立标准正态随机变量的平方和的分布。
-
卡方分布是 β 分布的特例
示例代码:
import numpy as np
from matplotlib import pyplot as pltdef gamma_function(n):cal = 1for i in range(2, n):cal *= ireturn caldef chi_squared(x, k):c = 1 / (2 ** (k/2)) * gamma_function(k//2)y = c * (x ** (k/2 - 1)) * np.exp(-x /2)return x, y, np.mean(y), np.std(y)for k in [2, 3, 4, 6]:x = np.arange(0, 10, 0.01, dtype=np.float)x, y, _, _ = chi_squared(x, k)plt.plot(x, y, label=r'$k=%d$' % (k))plt.legend()
plt.show()运行代码显示
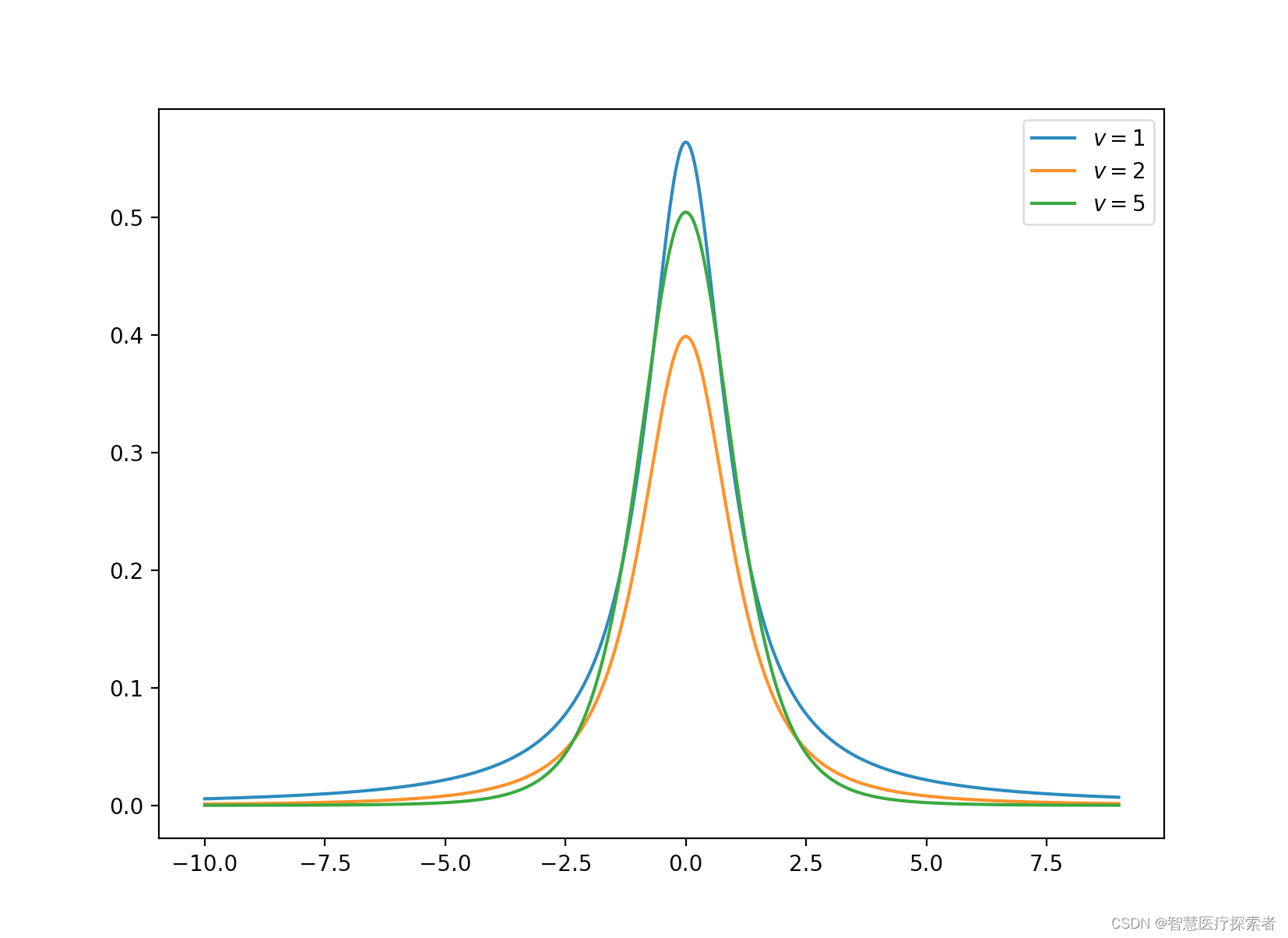
2.13 t 分布(连续)
t 分布是对称的钟形分布,与正态分布类似,但尾部较重,这意味着它更容易产生远低于平均值的值。
示例代码:
import numpy as np
from matplotlib import pyplot as pltdef gamma_function(n):cal = 1for i in range(2, n):cal *= ireturn caldef student_t(x, freedom, n):# divide [x.min(), x.max()] by nx = np.linspace(x.min(), x.max(), n)c = gamma_function((freedom + 1) // 2) \/ np.sqrt(freedom * np.pi) * gamma_function(freedom // 2)y = c * (1 + x**2 / freedom) ** (-((freedom + 1) / 2))return x, y, np.mean(y), np.std(y)for freedom in [1, 2, 5]:x = np.arange(-10, 10) # define range of xx, y, _, _ = student_t(x, freedom=freedom, n=10000)plt.plot(x, y, label=r'$v=%d$' % (freedom))plt.legend()
plt.show()运行代码显示
相关文章:

深度学习中的13种概率分布
1 概率分布概述 共轭意味着它有共轭分布的关系。 在贝叶斯概率论中,如果后验分布 p(θx)与先验概率分布 p(θ)在同一概率分布族中,则先验和后验称为共轭分布,先验称为似然函数的共轭先验。 多…...

C#基础知识 - 操作数与运算符篇2
C#基础知识 - 操作数与运算符篇 4.2 运算符4.2.1 按操作数个数分类4.2.2 按运算类型分类4.2.3 对运算符 、-- 的使用4.2.4 关系运算符:>、 < 、> 、<、 ! 、4.2.5 逻辑运算符:&& || ! ^ & |4.2.6 位运算符:~ 、^、 &…...
第十五章总结
一.输入/输出流 1.输入流 InputStrema类是字节输入流的抽象类,它是所有字节输入流的父类。 该类中所有方法遇到错误都会引发IOException异常。 read()方法:从输入流中读取数据的下一个字节。返回0~255的int字节值。如果因为已经到达流末尾而没有可用的…...

音频I2S
前言 基于网上资料对相关概念做整理汇总,部分内容引用自文后文章。 学习目标:简单了解相关概念、相关协议。 1 概述 数字音频接口DAI,即Digital Audio Interfaces,顾名思义,DAI表示在板级或板间传输数字音频信…...

小程序中的合法域名的作用及条件有哪些?
小程序的合法域名是指小程序项目中使用的各种接口、资源文件等所在的域名。在小程序开发中,需要将这些域名添加到小程序后台的“开发设置”-“服务器域名”中进行配置,才能够正常使用。 合法域名的作用: 1.作为小程序请求的 API 服务器域名…...
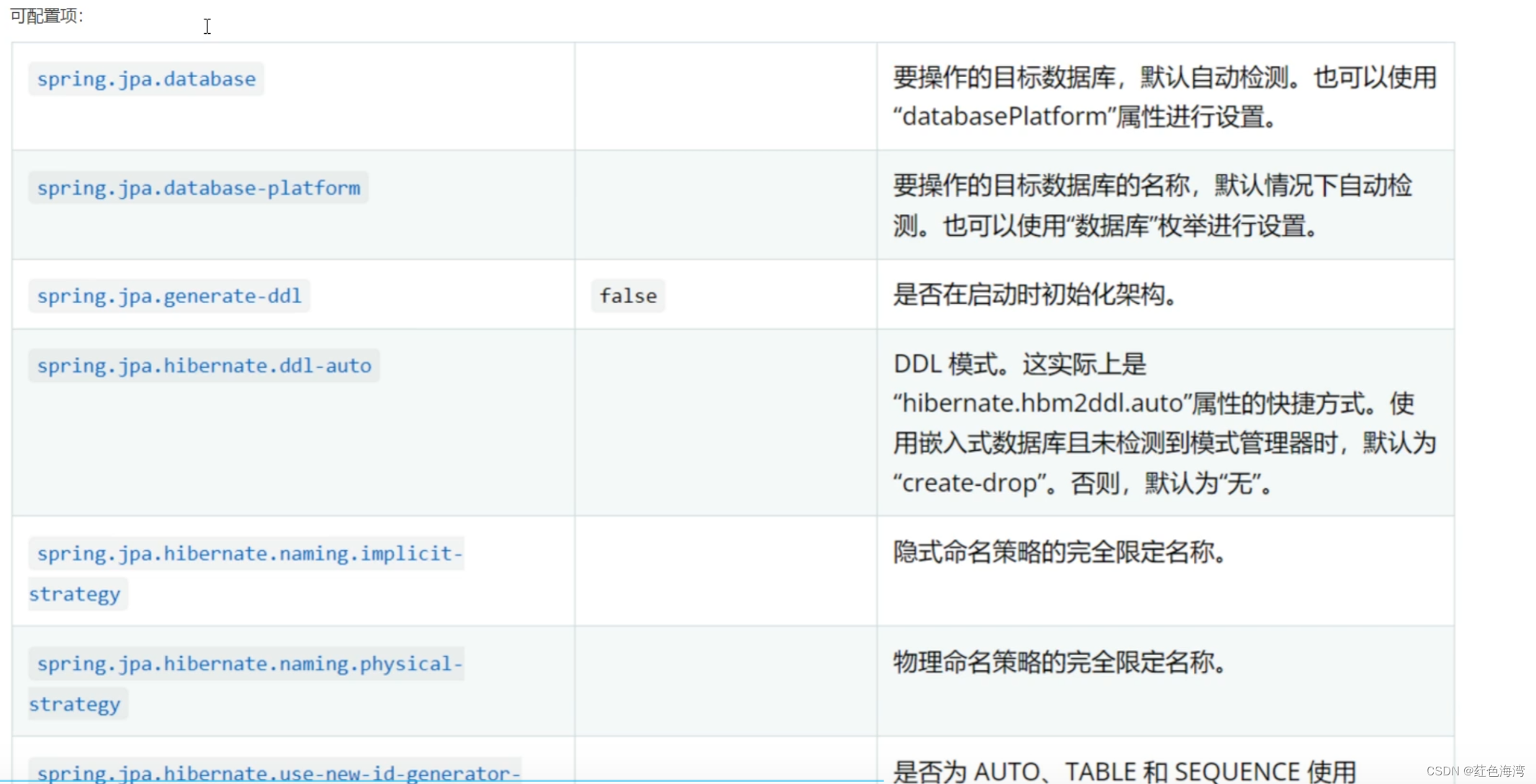
SpringData JPA 整合Springboot
1.导入依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0…...

打工人副业变现秘籍,某多/某手变现底层引擎-Stable Diffusion 黑白老照片上色修复
在这个时代,我们习惯于拥有高清、色彩丰富的照片,然而,那些古老的黑白色老照片由于年代的久远,往往会出现模糊、破损等现象。 那么今天要给大家介绍的是,用 Stable Diffusion 来修复老照片。 前段时间 ControlNet 的除了上线了“IP-Adapter”模型以外还增加另一个…...

第十三章总结
一.泛型 1.定义泛型类 泛型机制语法: 类名<T> 其中,T是泛型的名称,代表某一种类型。 【例13.6】创建带泛型的图书类 代码: 结果: 2.泛型的常规用法 (1)定义泛型类时声明多个变量 class MyClass<T1,T2…...

大模型应用_PrivateGPT
https://github.com/imartinez/privateGPT 1 功能 整体功能,想解决什么问题 搭建完整的 RAG 系统,与 FastGPT相比,界面比较简单。但是底层支持比较丰富,可用于知识库的完全本地部署,包含大模型和向量库。适用于保密级…...
[Android] ubuntu虚拟机上搭建 Waydroid 环境
1.安装虚拟机 略 2.安装waydroid Ubuntu/Debian and derivatives For Droidian and Ubuntu Touch, skip directly to the last step Install pre-requisites sudo apt install curl ca-certificates -y Add the official repository curl https://repo.waydro.id | sudo…...

LeedCode刷题---滑动窗口问题(二)
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂,年薪百万! 一、将X减到0的最小操作数 题目链接:将 x 减到 0 的最小操作数 题目描述 给你一个整数数组 nums 和一个整数 x 。每一…...
pycharm依赖管理(不要用pip freeze)
在使用python虚拟环境时,可以使用requirements.txt来管理当前项目的依赖。 注意,不要用 pip freeze > requirements.txt 这个命令,因为它会引入很多无关的包。 可以使用 pipreqs ./ --encodingutf-8 ./ 表示当前项目的目录࿰…...

[Kafka 常见面试题]如何保证消息的不重复不丢失
文章目录 Kafka1. Kafka如何保证不丢失消息?生产者数据的不丢失消费者数据的不丢失Kafka集群中的broker的数据不丢失 2. Kafka中的消息是否会丢失和重复消费?1. 消息发送2. 消息消费 3. Kafka 的设计是什么样的呢?4. 数据传输的事务定义有哪三…...
用法)
Java中System.setProperty()用法
Java中System.setProperty()用法 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天,让我们一起深入了解Java中的System.setProperty()方法,…...
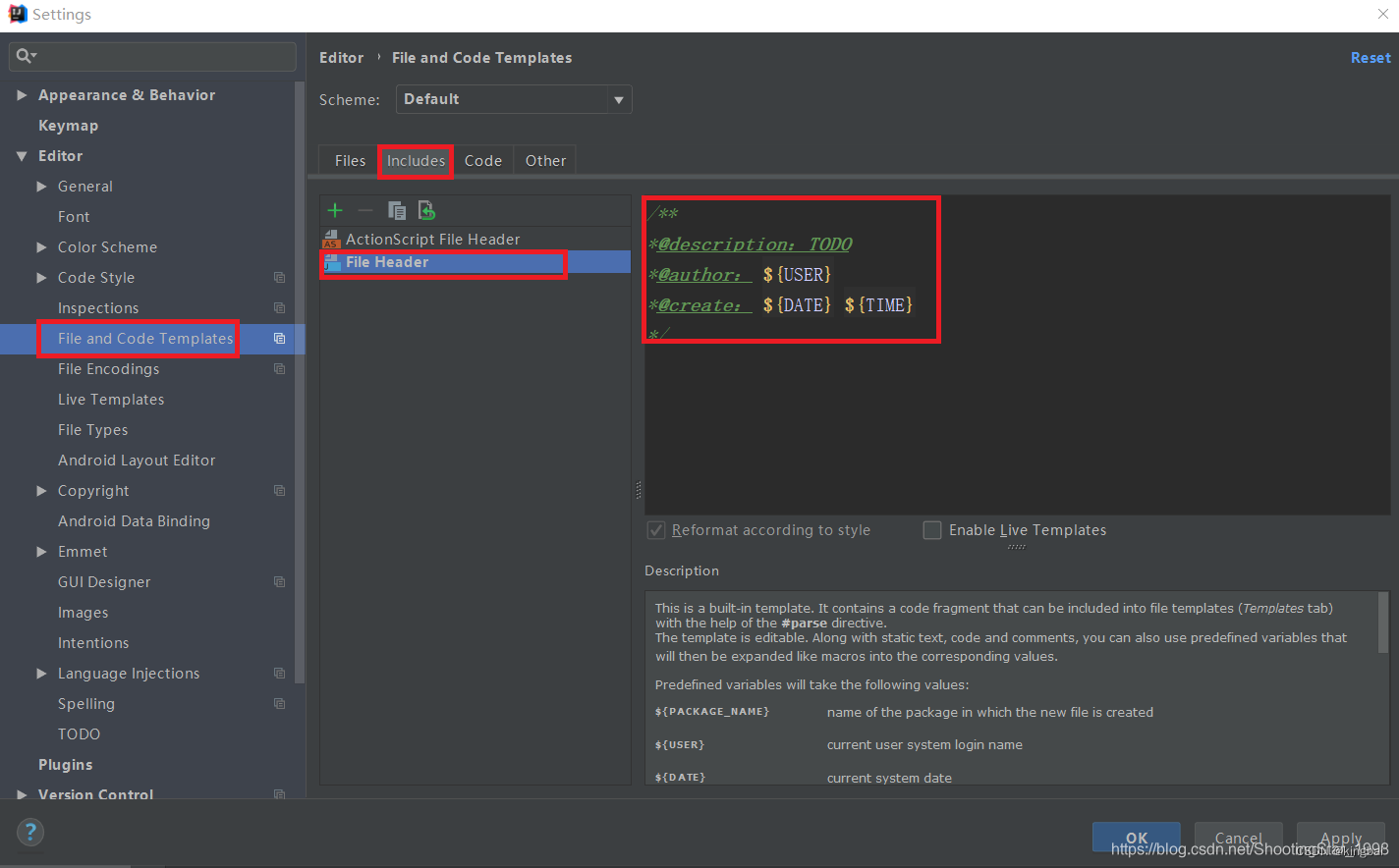
Eclipse 自动生成注解,如果是IDEA可以参考编译器自带模版进行修改
IDEA添加自动注解 左上角选择 File -> Settings -> Editor -> File and Code Templates; 1、添加class文件自动注解: /*** <b>Function: </b> todo* program: ${NAME}* Package: ${PACKAGE_NAME}* author: Jerry* date: ${YEA…...

微信小程序vant安装使用过程中遇到无法构建npm的问题
官网地址,然而如果完全按照这个教程来,实际上是缺少步骤的,需要补充一些步骤(参考https://www.bilibili.com/video/BV1vL41127Er) # 这步init就是补充的 npm init npm i vant/weapp -S --production# 剩下的按照vant的…...

[python]用python获取EXCEL文件内容并保存到DBC
目录 关键词平台说明背景所需库实现过程方法1.1.安装相关库2.代码实现 关键词 python、excel、DBC、openpyxl 平台说明 项目Valuepython版本3.6 背景 在搭建自动化测试平台的时候经常会提取DBC文件中的信息并保存为excel或者其他文件格式,用于自动化测试。本文…...

Spring Boot 如何配置 log4j2
Log4j2 介绍 Spring Boot 中默认使用 Logback 作为日志框架,接下来我们将学习如何在 Spring Boot 中集成与配置 Log4j2。在配置之前,我们需要知道的是 Log4j2 是 Log4j 的升级版,它在 Log4j 的基础上做了诸多改进: 异步日志&…...

如何安装docker
安装Docker的步骤取决于您使用的操作系统。以下是常见操作系统上安装Docker的基本步骤: 对于Linux: 更新软件包索引: sudo apt-get update安装允许apt通过HTTPS使用仓库的包: sudo apt-get install apt-transport-https ca-certificates cur…...

Linux 之 性能优化
uptime $ uptime -p up 1 week, 1 day, 21 hours, 27 minutes$ uptime12:04:11 up 8 days, 21:27, 1 user, load average: 0.54, 0.32, 0.23“12:04:11” 表示当前时间“up 8 days, 21:27,” 表示运行了多长时间“load average: 0.54, 0.32, 0.23”“1 user” 表示 正在登录…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

设计模式-3 行为型模式
一、观察者模式 1、定义 定义对象之间的一对多的依赖关系,这样当一个对象改变状态时,它的所有依赖项都会自动得到通知和更新。 描述复杂的流程控制 描述多个类或者对象之间怎样互相协作共同完成单个对象都无法单独度完成的任务 它涉及算法与对象间职责…...
