逛商场。。。
题目名字
逛商场
题意
见到想买的物品,只要能买得起,就一定会买下来之后才会继续往前走;如果买不起就直接跳过
思路
- 接着,它读取数组 aa 的值,并存储在数组中。
- 然后,程序读取一个整数 m。
- 初始化计数器 cnt 为0。
- 开始遍历数组 a。对于数组中的每个元素,如果它小于或等于 m,则:
将计数器 cnt加1。
从 m 中减去当前元素的值。
最后,程序输出计数器 cntcnt 的值。
坑点
1.要跳过买不了的,不能直接结束
实现步骤
- 接着,它读取数组 aa 的值,并存储在数组中。
- 然后,程序读取一个整数 m。
- 初始化计数器 cnt 为0。
- 开始遍历数组 a。对于数组中的每个元素,如果它小于或等于 m,则:
将计数器 cnt加1。
从 m 中减去当前元素的值。
最后,程序输出计数器 cntcnt 的值。
代码
#include<bits/stdc++.h>
using namespace std;
int main(){int n,a[100001],m;cin>>n;for(int i=1;i<=n;i++) cin>>a[i];cin>>m;int cnt=0;for(int i=1;i<=n;i++){if(m>=a[i]){cnt++;m-=a[i];}}cout<<cnt<<endl;return 0;
} 总结
x
相关文章:

逛商场。。。
题目名字 逛商场 题意 见到想买的物品,只要能买得起,就一定会买下来之后才会继续往前走;如果买不起就直接跳过 思路 接着,它读取数组 aa 的值,并存储在数组中。然后,程序读取一个整数 m。初始化计数器 cn…...

RTrPPG
研究背景 心率 (HR) 和脉搏率变异性 (PRV) 是允许分析心脏行为的两个生理参数。心率监测可以通过接触式和非接触式的两种方法进行。通常用于测量 HR 和 PRV 的两种接触式技术是心电图 (ECG) 和光电容积脉搏波 (PPG)。 ECG 测量由心脏活动引起的电场。另一方面,PPG …...
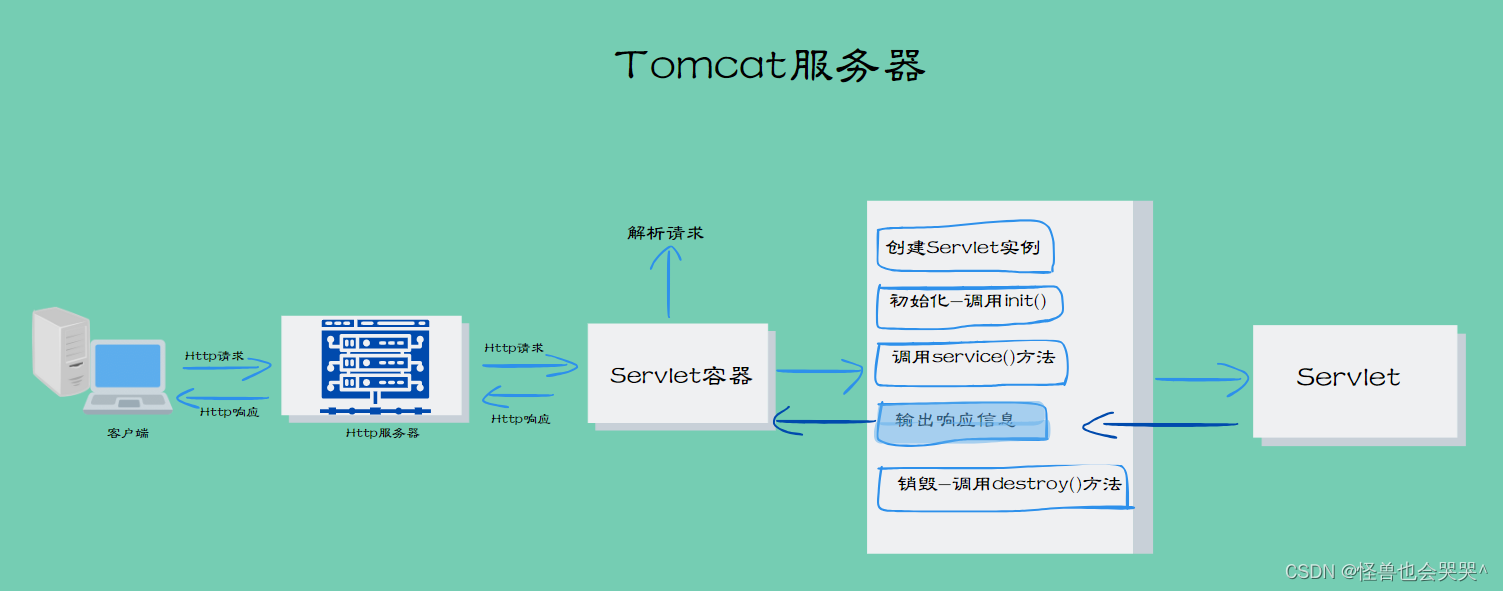
web应用开发技术的一些概念
一、Servlet 1.Servlet的工作过程: Servelt的工作流程示意图 (1)客户端发起一个Http请求到服务器,请求特定的资源或者是要执行特定的操作 (2)服务器在接收到请求后,根据请求相应的URL将请求分发…...

智能优化算法应用:基于乌燕鸥算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于乌燕鸥算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于乌燕鸥算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.乌燕鸥算法4.实验参数设定5.算法结果6.参考文…...
超聚变服务器(原华为服务器)网站模拟器
一、超聚变服务器(原华为服务器)网站模拟器: 原来了解服务器可以从他的网站上进行了解,模拟器做的很好了。 https://support.xfusion.com/server-simulators/ 有很多的模拟器,今天主要看下BMC的设置 有很多的在线工具…...
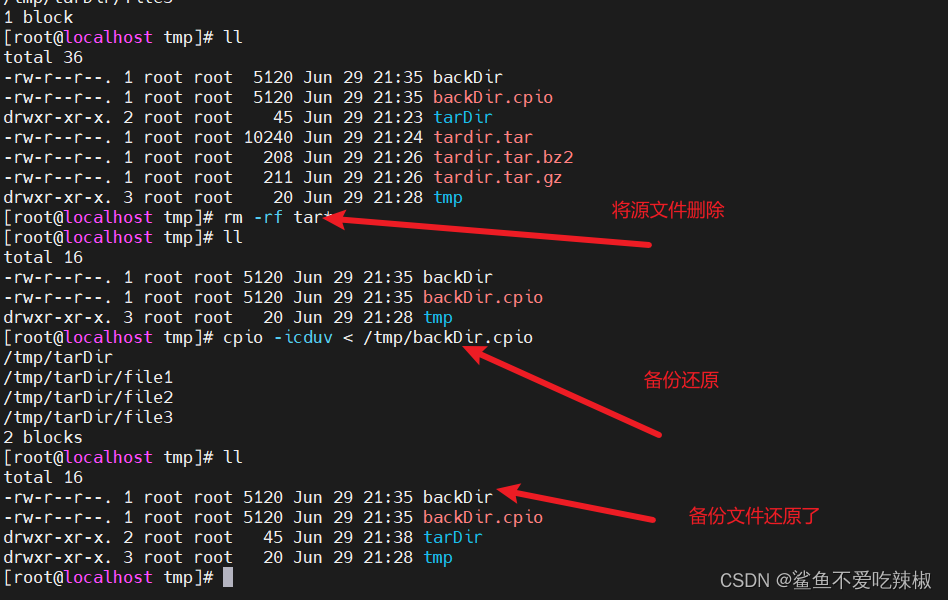
Linux常见压缩指令小结
为什么需要压缩技术 我们都知道文件是以byte作为单位的,如果我们的文件仅仅在低位占一个1 0000 0001这种情况我们完全可以压缩一下,将高位的0全部抹掉即可。 如上所说是一种压缩技术,还有一种就是将1111(此处省略96个)一共100个1࿰…...
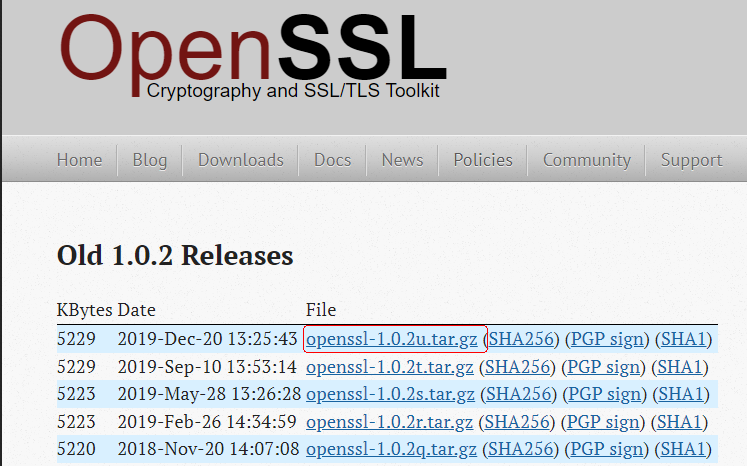
OpenSSL的源码在哪里下载?
官方网站去下载,网址: https://www.openssl.org/source/ 比较老的版本的下载页面地址: https://www.openssl.org/source/old/ 由于某面板的OpenSSL模块的安装配置语句如下: --with-openssl/root/rpmbuild/BUILD/openssl-1.0.2u所…...
使用create-react-app脚手架创建react项目
文章目录 1、安装create-react-app脚手架2、创建 React 项目,项目名为 react-demo3、项目创建成功4、使用vscode打开项目并运行5、项目运行成功node_modules:存放项目所依赖的一些第三方包文件public:静态资源文件夹src:源码文件夹其它文件 1…...
【网络安全】网络防护之旅 - 点燃网络安全战场的数字签名烟火
🌈个人主页:Sarapines Programmer🔥 系列专栏:《网络安全之道 | 数字征程》⏰墨香寄清辞:千里传信如电光,密码奥妙似仙方。 挑战黑暗剑拔弩张,网络战场誓守长。 目录 😈1. 初识…...
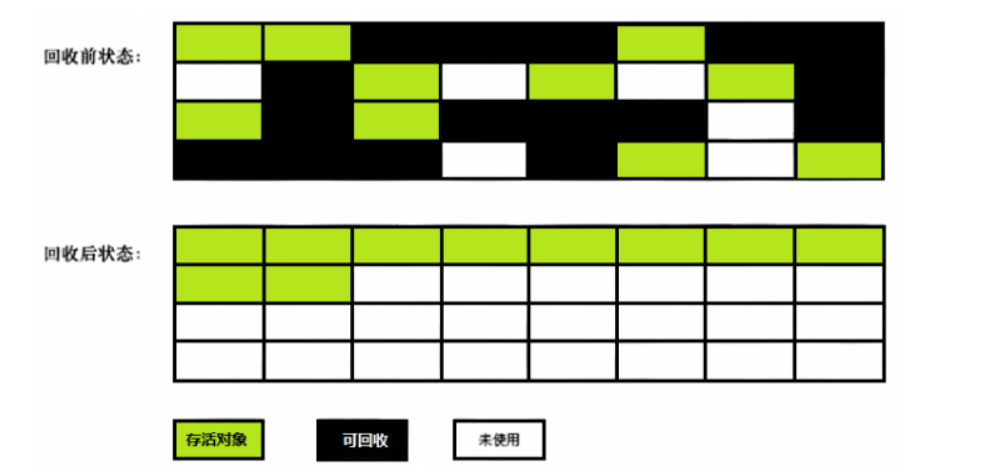
JVM基础扫盲
什么是JVM JVM是Java设计者用于屏蔽多平台差异,基于操作系统之上的一个"小型虚拟机",正是因为JVM的存在,使得Java应用程序运行时不需要关注底层操作系统的差异。使得Java程序编译只需编译一次,在任何操作系统都可以以相…...
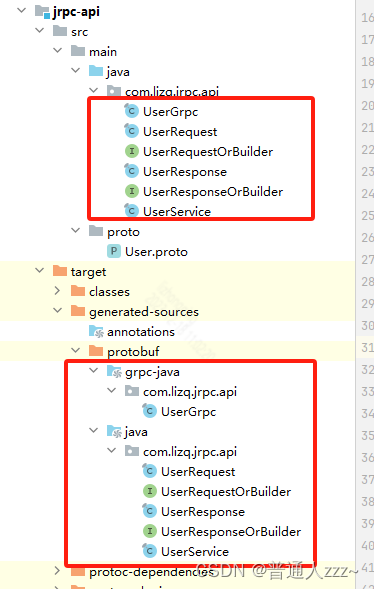
SpringBoot基于gRPC进行RPC调用
SpringBoot基于gRPC进行RPC调用 一、gRPC1.1 什么是gRPC?1.2 如何编写proto1.3 数据类型及对应关系1.4 枚举1.5 数组1.6 map类型1.7 嵌套对象 二、SpringBoot gRPC2.1 工程目录2.2 jrpc-api2.2.1 引入gRPC依赖2.2.2 编写 .proto 文件2.2.3 使用插件机制生产proto相关…...
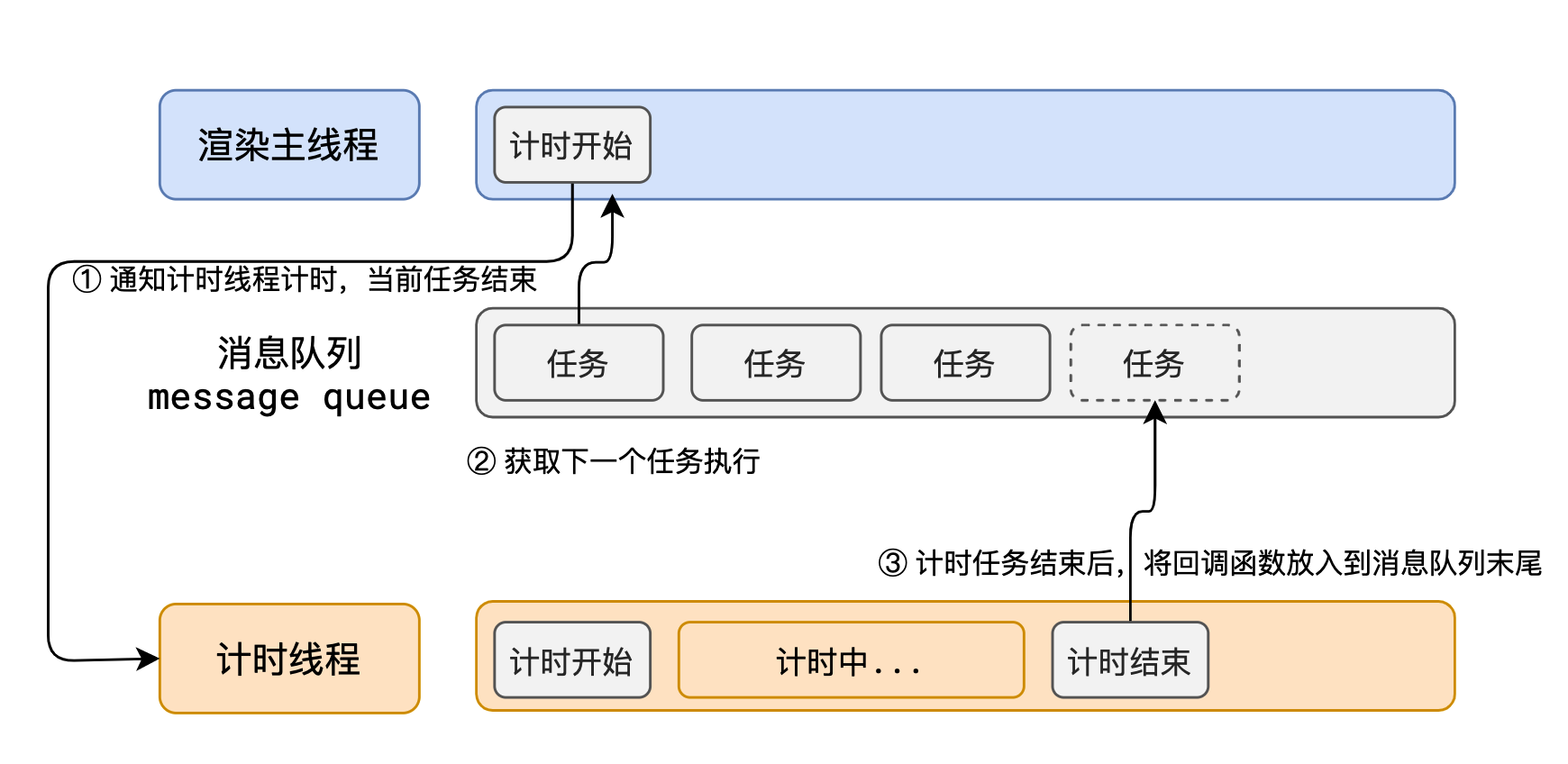
浏览器的事件循环机制(Event loop)
事件循环 浏览器的进程模型 何为进程? 程序运行需要有它自己专属的内存空间,可以把这块内存空间简单的理解为进程 每个应用至少有一个进程,进程之间相互独立,即使要通信,也需要双方同意。 何为线程? …...
THEMIS---Beta Sprint Summary Essay Blog
Which course does this assignment belong to2301-MUSE社区-CSDN社区云What are the requirements for this assignmentbeta SprintThe goal of this assignmentTo summarize the beta task progress and the teams sprintsTeam NameThemisTop-of-the-line collection of essa…...

Vue中实现分布式动态路由的基本实现步骤介绍
设想一下,我们在做一个体量非常大的项目,这个项目有很多的模块和相当多的页面。当我们想修改一个路由的时候,我们打开了router文件夹下的index.js文件时,一串长到鼠标滚轮需要滚大半天才滚到底的路由简直让人头皮发麻。 在开始之前…...

【Leetcode】计算器
思路 用栈来完成; 考虑到运算关系,先乘除后加减;此外,一般计算式首个数字式正数;判断字符是否为数字,str.isdigit()字符转数字:ord(str) - ord(‘0’)遇到加减符,压栈数字…...
巧妙的使用WPF中的资源
其实,在wpf中,最核心的就是xaml,因为只有xaml,才能体现出用的是wpf,而不是普通的cs文件,cs文件在winform中等等程序都可以使用的,唯独xaml才是wpf中最重要的,最精华的东西࿰…...

多维时序 | MATLAB实现RIME-CNN-BiLSTM-Multihead-Attention多头注意力机制多变量时间序列预测
多维时序 | MATLAB实现RIME-CNN-BiLSTM-Multihead-Attention多头注意力机制多变量时间序列预测 目录 多维时序 | MATLAB实现RIME-CNN-BiLSTM-Multihead-Attention多头注意力机制多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 MATLAB实现RIME-…...

【AIGC重塑教育】AI大模型驱动的教育变革与实践
文章目录 🍔现状🛸解决方法✨为什么要使用ai🎆彩蛋 🍔现状 AI正迅猛地改变着我们的生活。根据高盛发布的一份报告,AI有可能取代3亿个全职工作岗位,影响全球18%的工作岗位。在欧美,或许四分之一…...

【力扣100】2.两数相加
添加链接描述 # Definition for singly-linked list. # class ListNode: # def __init__(self, val0, nextNone): # self.val val # self.next next class Solution:def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Op…...
)
算法leetcode|93. 复原 IP 地址(多语言实现)
文章目录 93. 复原 IP 地址:样例 1:样例 2:样例 3:提示: 分析:题解:rust:go:c:python:java: 93. 复原 IP 地址: 有效 IP …...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
