「数据结构」二叉树1
🎇个人主页:Ice_Sugar_7
🎇所属专栏:C++启航
🎇欢迎点赞收藏加关注哦!
文章目录
- 🍉树
- 🍉二叉树
- 🍌特殊二叉树
- 🍌二叉树的性质
- 🍌存储结构
- 🍉堆
- 🍌堆的结构
- 🍌插入
- 🥝向上调整算法
- 🫐时间复杂度分析
- 🍌删除
- 🥝向下调整算法
- 🫐时间复杂度分析
- 🍌堆的创建(堆的初始化)
- 🍌堆排序
- 🍌top k 问题
- 🍉写在最后
🍉树
●树是一种非线性的数据结构,它是由n(n>=0)个结点组成,具有层次关系
●有一个特殊的结点,称为根结点,根节点没有前驱结点
●除根节点外,其余结点被分成M(M>0)个互不相交的集合,每个集合是一棵子树
🍉二叉树
二叉树一个非空结点的子树为空或者至多两个子树(左子树和右子树)

从这个图可以看出:
二叉树不存在度大于2的结点
二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
🍌特殊二叉树
满二叉树:每一层结点数都达到最大值的二叉树。如果一棵满二叉树有k层,那它结点总数就是2^k-1
完全二叉树:最后一层抠掉几个结点的满二叉树,就是一般的完全二叉树(满二叉树是特殊的完全二叉树)
🍌二叉树的性质
二叉树的性质都在下图了:


🍌存储结构
二叉树一般使用两种结构存储:顺序结构和链式结构
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实使用中只有堆才会使用数组来存储
二叉树顺序存储在物理结构上是一个数组,在逻辑结构上是一颗二叉树
我们的代码是按照其物理结构写的,而具体想实现的函数接口则是根据逻辑结构展开的(往下看入堆、出堆、调整等函数之后,你就能理解这句话了)
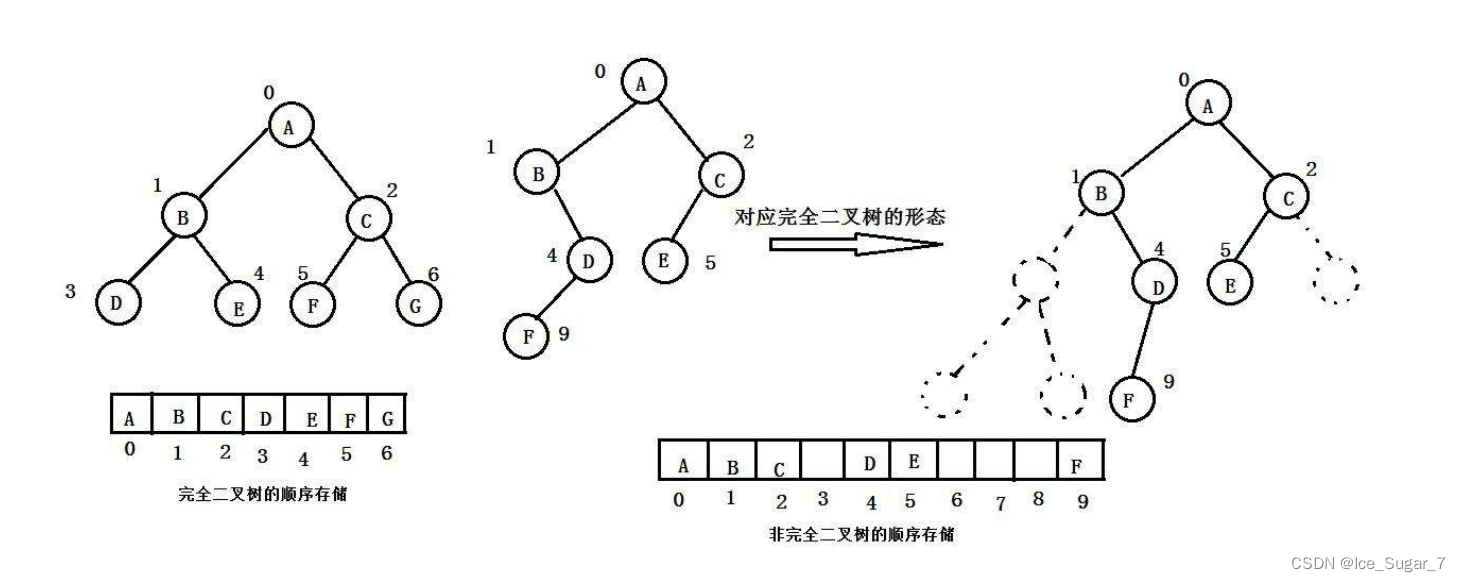
本文讲二叉树的顺序存储结构——堆(正文开始)
🍉堆
堆分为两种:大堆和小堆。
大堆:除了叶子结点外,所有结点的孩子都比自己小
小堆:除了叶子结点外,所有结点的孩子都比自己大
根据堆的逻辑结构可知,大堆是上面的结点(位于较低层次的结点)大,小堆是上面的结点小
🍌堆的结构
堆的物理结构就是顺序表,所以代码基本和顺序表一模一样
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;
🍌插入
插入这一步很简单,就直接往数组插入元素(注意检查容量是否足够,并且插入后记得让size加1)
插入后,要对这个元素进行调整,采用向上调整
🥝向上调整算法
假设要建一个小堆,那就要拿它和它的双亲进行比较,如果它比双亲小,就和双亲交换位置。假设数组名为_a,大小为size,那插入的结点下标为size-1,它的双亲在数组中的下标就是(size-1-1)/2
这里要用循环,将插入的结点记为child,当child为0时(即它到了堆顶),循环终止。如果中途经比较后发现不用换位置的话,说明调整好了,直接break跳出循环
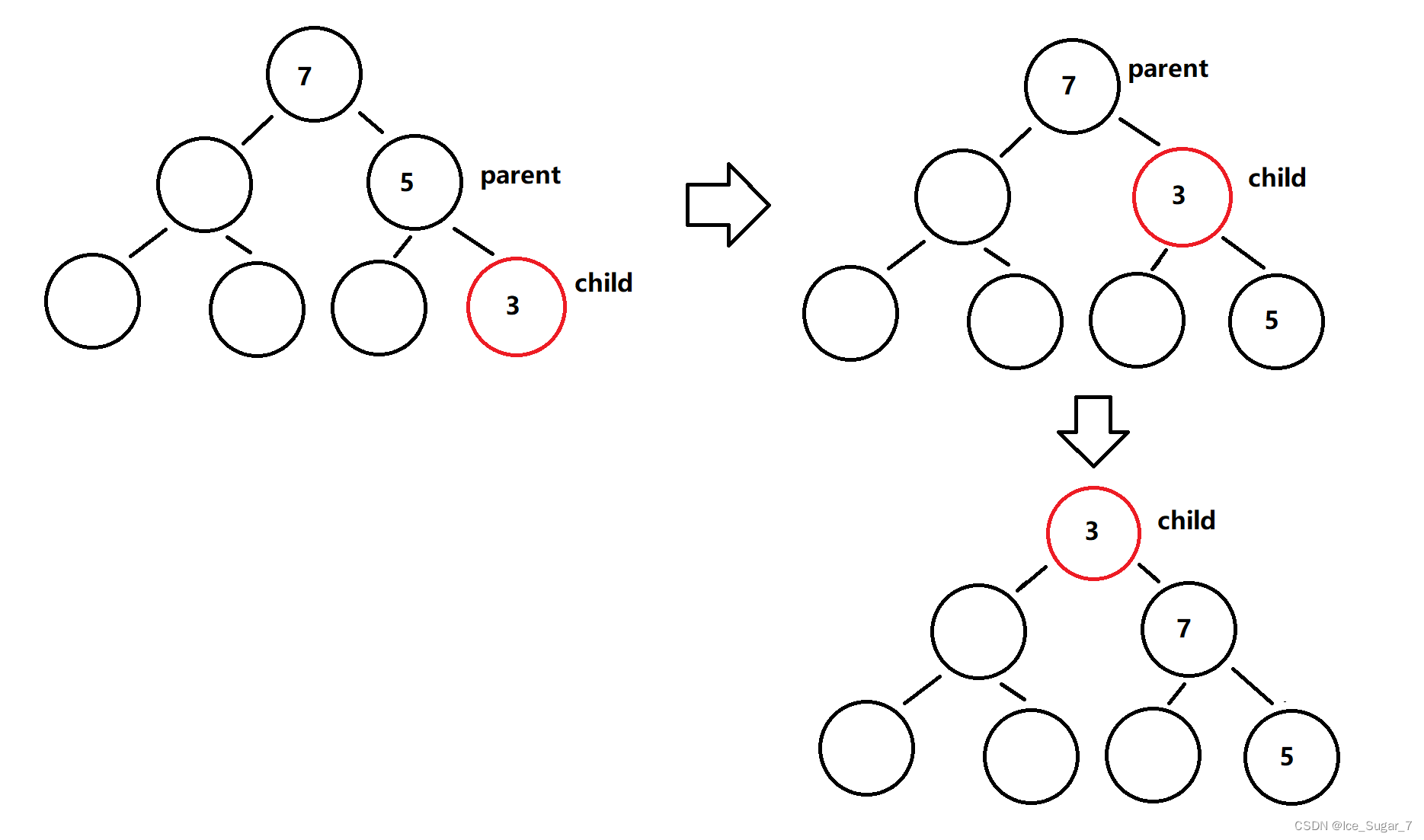
代码如下:
typedef int HPDataType;void Swap(HPDataType* hp1, HPDataType* hp2) {HPDataType tmp = *hp1;*hp1 = *hp2;*hp2 = tmp;
}//小堆向上调整
void AdjustUp(Heap* hp,int child) {assert(hp);int parent = (child - 1) / 2;while (child > 0) {if (hp->_a[child] >= hp->_a[parent]) //孩子比双亲大,退出循环break;else {Swap(&(hp->_a[child]),&(hp->_a[parent])); //两结点交换child = parent;parent = (parent - 1) / 2;}}
}
🫐时间复杂度分析
因为堆是完全二叉树,而满二叉树也是完全二叉树,为了简化问题,就用满二叉树来证明了(时间复杂度本来看的就是近似值,多几个节点不影响最终结果),下面向下调整算法的时间复杂度也这样处理
假设有n个结点,那就有log(n+1)层,那每次向下调整最多遍历log(n+1)次,总共有n个结点,那么就遍历n*log(n+1)次,时间复杂度就是O(N*logN)
🍌删除
不能直接将数组往前挪一位,因为这样虽然在物理结构(数组)上没什么问题,但是在逻辑结构(完全二叉树)上就有问题了,会打乱结点间的关系(比如原先的兄弟现在变为父子,父子变兄弟)
有一个比较巧妙的解决办法,就是将根结点和尾结点(数组最后一个元素)交换位置,然后将新的尾结点删掉,这样就不会影响到结点间的关系了
删掉后要进行向下调整,这就涉及到向下调整算法了
🥝向下调整算法
现在有一个数组,它有n个元素,从逻辑结构上看成是完全二叉树,我们从根结点开始,通过向下调整算法可以把它调整为一个小堆
这种算法的前提是左右子树必须是一个堆,才能调整
int array[] = {27,15,19,18,28,34,65,49,25,37};
调整过程如图:

每次调整,先比较该结点两个孩子的大小,现在要调整为小堆,就先找出较小的孩子,然后这个孩子和双亲进行比较,若孩子<双亲,就把它和双亲交换位置;反之则说明调整完毕
调整的过程显然也要用循环。我们将双亲结点记为parent,左孩子结点记为child(因为左右孩子下标相差1,没必要用leftchild和rightchild进行区分)。那右孩子就是child + 1,不过由于右孩子可能不存在(当child为叶子结点时可能会有这种情况),所以我们得在循环里面判断一下
这里采用假设法,就是我们先假设左孩子是较小的结点(因为右孩子可能不存在,不方便假设),如果右孩子存在的话,就拿左右孩子进行比较,最后将child赋给较小者
(假设法相比于if语句,可以有效简化代码,具体可以看我之前那篇判断相交链表的题解,or看下面的代码也ok)文章链接:判断相交链表
那循环的终止条件呢?显然当child>=n的时候就要跳出循环了
代码如下:
void AdjustDown(HPDataType* a,int n,int parent) { //n为数组大小assert(a);int child = 2 * parent + 1; //左孩子下标while (child < n) {if (child + 1 < n && a[child+1] <= a[child]) { //右结点存在并且右孩子比左孩子小child++; //将child设为右孩子结点,等会儿拿它和双亲进行比较,决定是否交换}if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);parent = child; //更新双亲结点child = parent * 2 + 1; //更新孩子结点}elsebreak; //不用换位置说明调整完毕}
}
🫐时间复杂度分析
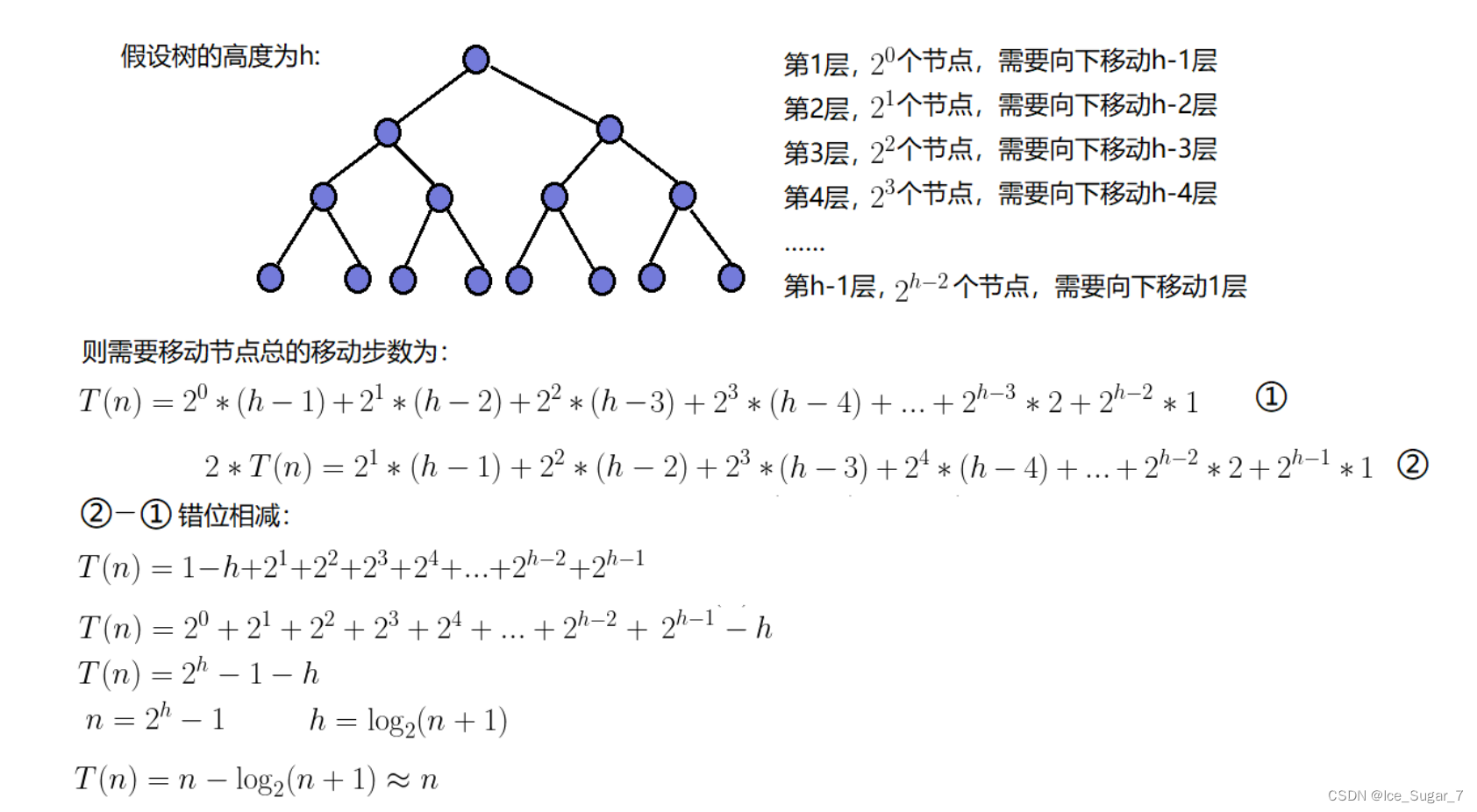
“向下移动”的层数指的是最多要调整几次,即从这个结点开始,一直调整到叶子结点为止(最坏的情况)
从结果可以看出:向下调整的时间复杂度(O(N))比向上调整的小,所以建议使用向下调整
🍌堆的创建(堆的初始化)
建堆既可以建一个空堆,也可以根据一个现成的数组建堆
建空堆就是将数组赋为空指针,然后size和capacity都赋为0。和顺序表初始化一样,不多赘述
这里主要来讲数组建堆
思路是:给堆开辟空间+拷贝+调整
●开空间:数组多大就开多大
●拷贝:使用memcpy将数组的元素拷贝给堆
●调整:向上调整or向下调整
先展示向上调整
void HeapCreate(Heap* hp, HPDataType* a, int n) {assert(hp);assert(a);HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType) * n);if (tmp == NULL) {perror("malloc fail");exit(-1);}hp->_a = tmp;hp->_capacity = hp->_size = n;memcpy(hp->_a, a, n * sizeof(HPDataType)); //把数组数据拷贝到堆的数组中int parent = (hp->_size - 1) / 2;for (int i = 1; i < n; i++) { // 调整建堆AdjustUp(hp, i);}
}
也可以复用刚才写的入堆函数,因为它自带向上调整函数。而且push函数是将数组的元素一个一个放进堆的,这样就不需要memcpy了,代码如下(为方便观察,我把向上调整函数和入堆函数也放在下面):
//小堆向上调整
void AdjustUp(Heap* hp, int child) {assert(hp);int parent = (child - 1) / 2;while (child > 0) {if (hp->_a[child] >= hp->_a[parent]) //孩子比双亲大,退出循环break;else {Swap(hp->_a[child], hp->_a[parent]); //两结点交换child = parent;parent = (child - 1) / 2;}}
}void HeapPush(Heap* hp, HPDataType x) {assert(hp);//如果满了 那就要扩容if (hp->_capacity == hp->_size) {int newcapacity = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;HPDataType* tmp = (HPDataType*)realloc(hp->_a, newcapacity * sizeof(HPDataType));if (tmp == NULL) {perror("realloc fail");exit(-1);}hp->_a = tmp;hp->_capacity = newcapacity;}hp->_a[hp->_size] = x;hp->_size++;AdjustUp(hp, hp->_size - 1);
}void HeapCreate(Heap* hp, HPDataType* a, int n) {assert(hp);HeapInit(hp); //初始化为空堆for (int i = 0; i < n; ++i) {HeapPush(hp, a[i]);}
}
由于向上调整的效率不及向下调整,所以建议采用向下调整建堆
向下调整要求左子树和右子树也都是堆,又因为单个叶子结点既可以看作是大堆,也可以看成小堆,所以我们从叶子结点的双亲开始向下调整
比如下面这个数组要建一个大堆
int a[] = {4,3,5,7,2,6,8,65,100,70,32,50,60};
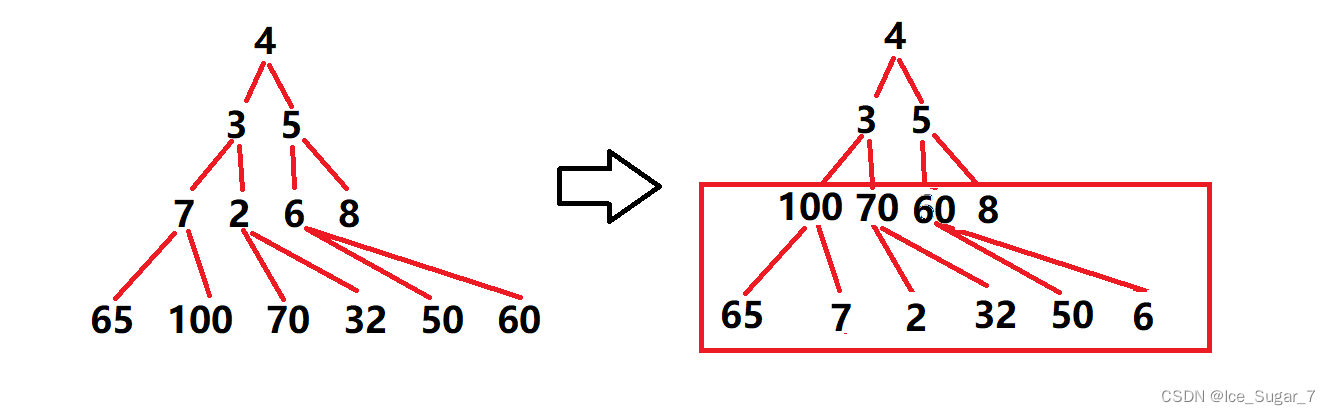
调整后,红色方框内就是一个大堆了,对于3,5这两个结点而言,左右子树都是大堆,那它们也可以向下调整了
代码如下:
void HeapCreate(Heap* hp, HPDataType* a, int n) {assert(hp);HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType) * n);if (tmp == NULL) {perror("malloc fail");exit(-1);}hp->_a = tmp;hp->_capacity = hp->_size = n;memcpy(hp->_a, a, n * sizeof(HPDataType)); //把数组数据拷贝到堆的数组中int parent = (hp->_size - 1 - 1) / 2; //最后一个结点的双亲结点for (int i = parent; i >= 0;i--) { //从该结点开始进行向下调整AdjustDown(hp->_a, n, i);}
}
🍌堆排序
现在有一个数组,要把它排成升序
如果建小堆,那么很容易就可以找到最小的元素。但是要找次小元素的时候,把数组剩下的元素看作完全二叉树的话,它们之间的关系会乱掉
●所以要建大堆,建好后最大的元素就在根结点,将它和最后一个结点交换,就把最大的元素排好了
●然后size-1剔除最大的元素,对于剩下的元素,因为根结点的左右子树也都是大堆,可以采用向下调整,调整后可以把第二大的元素移动到堆顶(根结点),再和最后一个结点交换,第二大元素就排好了
●剩下的元素也如法炮制
void HeapSort(int* a, int k) { //a为给定数组for (int i = (k - 1 - 1) / 2; i >= 0; i--) { //调整为一个堆AdjustDown(a, k, i);}for (int i = k - 1; i >= 0; i--) { //采用删除结点的思想,先交换,再调整Swap(a[0], a[i]);AdjustDown(a, i, 0);}
}
排序后得到:

🍌top k 问题
这个问题就是要找出数组中从大到小(或从小到大)的前k个数,下面以从大到小为例
如果要找从大到小的前k个数,我们可以先从数组中选k个数,建一个大小为k的小堆,然后将数组中剩下的数和堆顶的数进行比较,如果比它大,就替代它,然后向下调整。
这个方法的原理是:放一个比较小的数“卡”在堆顶,类似守门员,比它大的数就能进堆,不断把堆中较小的数踢出去,到最后就留下最大的前k个数
//取最大的前k个
void TopK(HPDataType* pa, int n, int k) {Heap ph;HeapInit(&ph);HeapCreate1(&ph, pa, k); //建小堆for (int i = k; i < n; i++) //遍历剩下的元素{if (pa[i] > ph._a[0]) {ph._a[0] = pa[i];AdjustDown(ph._a, k, 0); //小堆向下调整}}HeapSort(ph._a, k); //将得到前k数进行排序HeapPrint(&ph);
}
🍉写在最后
以上就是本篇文章的全部内容,如果你觉得本文对你有所帮助的话,那不妨点个小小的赞哦!(比心)
相关文章:

「数据结构」二叉树1
🎇个人主页:Ice_Sugar_7 🎇所属专栏:C启航 🎇欢迎点赞收藏加关注哦! 文章目录 🍉树🍉二叉树🍌特殊二叉树🍌二叉树的性质🍌存储结构 🍉…...
栈(C语言版)
一.栈的概念及结构 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。 进行数据插入和删除操作的一端 称为栈顶,另一端称为栈底。 栈中的数据元素遵守 后进先出 LIFO ( Last In First Out )的原则。…...

聊聊reactor-logback的AsyncAppender
序 本文主要研究一下reactor-logback的AsyncAppender AsyncAppender reactor-logback/src/main/java/reactor/logback/AsyncAppender.java public class AsyncAppender extends ContextAwareBaseimplements Appender<ILoggingEvent>, AppenderAttachable<ILogging…...
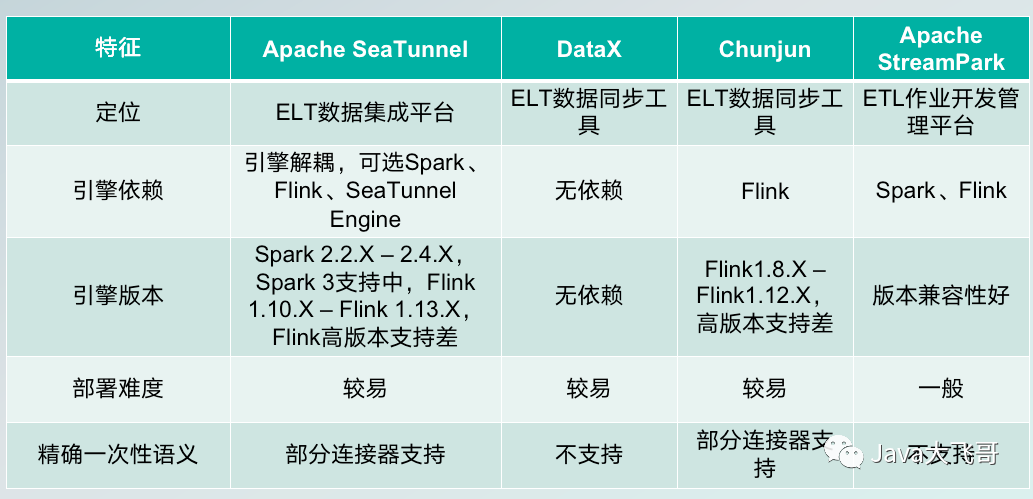
Apache SeaTunne简介
Apache SeaTunne简介 文章目录 1.Apache SeaTunne是什么?1.1[官网](https://seatunnel.apache.org/)1.2 项目地址 2.架构3.特性3.1 丰富且可扩展的连接器和插件机制3.2 支持分布式快照算法以确保数据一致性3.3 支持流、批数据处理,支持全量、增量和实时数…...

【开题报告】基于uniapp的IT资讯阅读小程序的设计与实现
1.研究背景 随着信息技术的飞速发展和互联网的普及,IT(Information Technology)行业成为了当今社会中最活跃和最具前景的领域之一。人们对于IT领域的资讯需求越来越高,希望能够第一时间获取到全面、准确、及时的IT资讯。 传统的…...

Java小案例-SpringBoot火车票订票购票票务系统
目录 前言 详细资料 源码获取 前言 SpringBoot火车票订票购票票务系统 前端使用技术:HTML5,CSS3、JavaScript、VUE等 后端使用技术:Spring boot(SSM)等 数据库:Mysql数据库 数据库管理工具:phpstud…...

关于获取高级电工职业技能等级证书一些避坑经历
有幸在今年9月份成功通过高级电工职业技能等级认证,以下是我遇到的一些常见问题,以及一些考点内容以及总结 什么是高级电工职业技能等级证书 电工职业技能等级证书是证明持证人电工知识和技能水平高低的,是持证人应聘、求职、任职、开业的资格凭证,是用…...

springboot(ssm在线课程管理系统 网课管理系统Java系统
springboot(ssm在线课程管理系统 网课管理系统Java系统 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0) 数…...
4.1 媒资管理模块 - Nacos与Gateway搭建
文章目录 媒资管理模块 - 媒资项目搭建一、需求分析1.1 介绍1.2 数据模型1.3 分析网关 二、 搭建Nacos2.1 服务发现中心2.2.1 Maven2.2.2 配置Nacos 2.2 配置中心2.2.1 介绍2.2.2 Maven 坐标2.2.3 配置 content-api 工程2.2.4 配置 content-service 工程2.2.5 配置 system-api …...

1641:【例 1】矩阵 A×B
【题目描述】 矩阵 A 规模为 nm ,矩阵 B 规模为 mp ,现需要你求 AB 。 矩阵相乘的定义:nm 的矩阵与 mp 的矩阵相乘变成 np 的矩阵,令 aik 为矩阵 A 中的元素,bkj 为矩阵 B 中的元素,则相乘所得矩阵 C 中的…...

iOS问题记录 - iOS 17通过NSUserDefaults设置UserAgent无效
文章目录 前言开发环境问题描述问题分析解决方案最后 前言 最近维护一个老项目时遇到的问题。说起这老项目我就有点头疼,一个快十年前的项目,这么说你可能不觉得有什么,但是你想想Swift也才发布不到十年(2014年6月发布࿰…...

linux的一些典型面试题解读
目录 前言1 Linux 文件系统2 Shell 编程3 进程管理4 用户和权限管理5 软件包管理6 网络配置7 系统监控和日志8 存储管理9 安全性10 常见命令11 系统启动流程12 Linux 进程间通信方式13 Linux 中的 I/O 多路复用14 Shell 脚本优化与调试15 Linux 文件权限与 ACL16 Linux 中的环境…...

tortoisesvn各版本下载链接
https://tortoisesvn.net 无法访问最新版本下载 TortoiseSVN download | SourceForge.net 所有版本下载 TortoiseSVN - Browse Files at SourceForge.net...
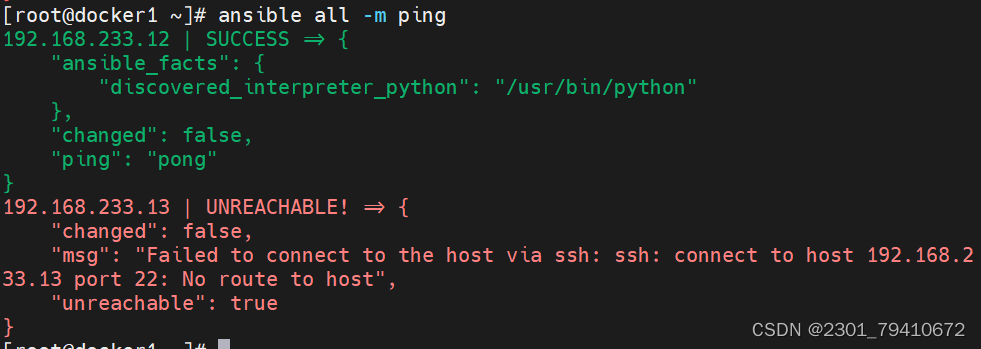
[自动化运维工具]ansible简单介绍和常用模块
ansible 源操作主机功能 自动化运维(playbook剧本yaml) 是基于python开发的一个配置管理和应用部署工具,在自动化运维中,现在还是异军突起 ansible能批量配置,部署,管理上千台主机,类似于xshell…...

记一次渗透测试信息收集-越权
目录 一、信息收集 子域名收集 存活探测 二、越权 越权一 越权二 一、信息收集 子域名收集 使用subfinder进行子域名收集 语法:subfinder.exe -d xx.com -all -o qq1.txt -v //结合自己渗透经验,多渠道收集子域名,汇总去重。 …...

Flink系列之:Table API Connectors之JSON Format
Flink系列之:Table API Connectors之JSON Format 一、JSON Format二、依赖三、创建一张基于 JSON Format 的表四、Format 参数五、数据类型映射关系 一、JSON Format JSON Format 能读写 JSON 格式的数据。当前,JSON schema 是从 table schema 中自动推…...

2018年第七届数学建模国际赛小美赛B题世界杯足球赛的赛制安排解题全过程文档及程序
2018年第七届数学建模国际赛小美赛 B题 世界杯足球赛的赛制安排 原题再现: 有32支球队参加国际足联世界杯决赛阶段的比赛。但从2026年开始,球队的数量将增加到48支。由于时间有限,一支球队不能打太多比赛。因此,国际足联提议改变…...
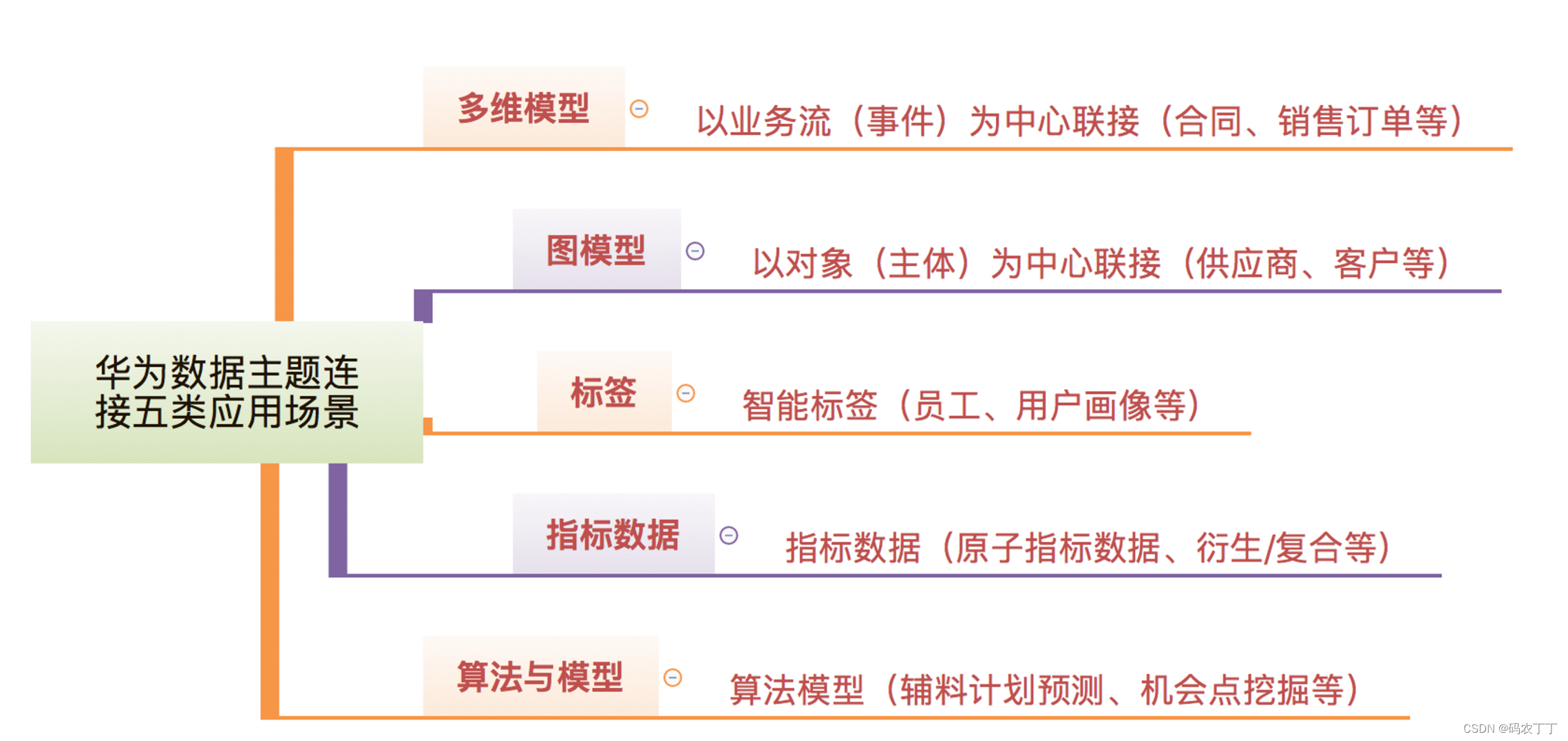
【为数据之道学习笔记】5-7五类数据主题联接的应用场景
在数字化转型的背景下,华为的数据消费已经不再局限于传统的报表分析,还要支持用户的自助分析、实时分析,通过数据的关联,支持业务的关联影响分析以及对目标对象做特征识别,进行特定业务范围圈定、差异化管理与决策等。…...
得帆信息创始人-张桐,受邀出席 BV百度风投AIGC主题论坛
近日,得帆信息创始人兼CEO张桐,作为百度风投被投代表企业创始人受邀出席“向未来,共成长” BV百度风投AIGC主题论坛。 与包括上海市徐汇区相关部门领导、百度集团相关事业部负责人及代表,以及来自国寿资本、中网投、麦顿投资的投资…...

云原生之深入解析减少Docker镜像大小的优化技巧
一、什么是 Docker? Docker 是一种容器引擎,可以在容器内运行一段代码,Docker 镜像是在任何地方运行应用程序而无需担心应用程序依赖性的方式。要构建镜像,docker 使用一个名为 Dockerfile 的文件,Dockerfile 是一个包…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...
)
零基础在实践中学习网络安全-皮卡丘靶场(第十一期-目录遍历模块)
经过前面几期的内容我们学习了很多网络安全的知识,而这期内容就涉及到了前面的第六期-RCE模块,第七期-File inclusion模块,第八期-Unsafe Filedownload模块。 什么是"遍历"呢:对学过一些开发语言的朋友来说应该知道&…...

break 语句和 continue 语句
break语句和continue语句都具有跳转作用,可以让代码不按既有的顺序执行 break break语句用于跳出代码块或循环 1 2 3 4 5 6 for (var i 0; i < 5; i) { if (i 3){ break; } console.log(i); } continue continue语句用于立即终…...
多模态学习路线(2)——DL基础系列
目录 前言 一、归一化 1. Layer Normalization (LN) 2. Batch Normalization (BN) 3. Instance Normalization (IN) 4. Group Normalization (GN) 5. Root Mean Square Normalization(RMSNorm) 二、激活函数 1. Sigmoid激活函数(二分类&…...

Redis专题-实战篇一-基于Session和Redis实现登录业务
GitHub项目地址:https://github.com/whltaoin/redisLearningProject_hm-dianping 基于Session实现登录业务功能提交版本码:e34399f 基于Redis实现登录业务提交版本码:60bf740 一、导入黑马点评后端项目 项目架构图 1. 前期阶段2. 后续阶段导…...
