《代码随想录》--二叉树(一)
《代码随想录》--二叉树 第一部分
- 1、二叉树的递归遍历
- 2、二叉树的迭代遍历
- 3、统一风格的迭代遍历代码
- 4、二叉树的层序遍历
- 226.翻转二叉树
1、二叉树的递归遍历
前序遍历
中序遍历
后序遍历
代码
- 前序遍历
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();preOrder(root,list);return list;}public void preOrder(TreeNode root,List<Integer> list){if(root == null) return;list.add(root.val);preOrder(root.left,list);preOrder(root.right,list);}
}
- 中序遍历
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();inOrder(root,list);return list;}public void inOrder(TreeNode root,List<Integer> list){if(root == null) return;inOrder(root.left,list);list.add(root.val);inOrder(root.right,list);}
}
- 后序遍历
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();postOrder(root,list);return list;}public void postOrder(TreeNode root,List<Integer> list){if(root == null) return;postOrder(root.left,list);postOrder(root.right,list);list.add(root.val);}
}
2、二叉树的迭代遍历
前序遍历
中序遍历
后序遍历
代码
- 前序遍历
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if(root == null) return result;Stack<TreeNode> stack = new Stack<>();stack.push(root);while(!stack.isEmpty()){TreeNode node = stack.pop();result.add(node.val);if(node.right != null) stack.push(node.right);if(node.left != null) stack.push(node.left);}return result;}
}
- 中序遍历
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while(cur != null || !stack.isEmpty()){if(cur != null){stack.push(cur);cur = cur.left;}else{TreeNode node = stack.pop();list.add(node.val);cur = node.right;}}return list;}
}
- 后序遍历
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if(root == null) return list;Stack<TreeNode> stack = new Stack<>();stack.push(root);while(!stack.isEmpty()){TreeNode node = stack.pop();list.add(node.val);if(node.left != null) stack.push(node.left);if(node.right != null) stack.push(node.right);}Collections.reverse(list);return list;}
}
分析
- 非递归的遍历都需要借助栈来编写代码
- 前序遍历:
- 前序遍历是中左右的顺序
- 先把中间节点放入栈中
- 再放入右孩子(为什么?因为栈先入后出)
- 再放入左孩子
- 中序遍历:
- 中序遍历的顺序是左中右,但是我们的处理顺序和访问顺序不一致,所以借助指针
- 定义一个
cur指针帮助我们遍历,栈用来处理节点上的元素
- 后序遍历:
- 后序遍历的顺序是左右中,可以根据前序遍历改变得到
- 将遍历顺序改为中左右,最后得到的结果是中右左
- 反转数组得到正确结果
3、统一风格的迭代遍历代码
- 前面的迭代遍历代码风格不统一,不像递归代码一样修改代码的位置就能写出三种遍历方式
- 这里借助空节点标记法
代码
- 前序
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();if(root != null) stack.push(root);while(!stack.isEmpty()){TreeNode node = stack.peek();if(node != null){node = stack.pop();if(node.right != null) stack.push(node.right);if(node.left != null) stack.push(node.left);stack.push(node);stack.push(null);}else{stack.pop();node = stack.pop();list.add(node.val);}}return list;}
}
- 中序
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();if(root != null) stack.push(root);while(!stack.isEmpty()){TreeNode node = stack.peek();if(node != null){node = stack.pop(); //将该节点弹出if(node.right != null) stack.push(node.right); //添加左节点stack.push(node); //添加中节点stack.push(null); //中间节点访问过,但是还没有处理,加入空节点标记if(node.left != null) stack.push(node.left); //添加右节点}else{stack.pop(); //弹出空节点node = stack.pop(); //取出栈中元素list.add(node.val);}}return list;}
}
- 后序
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();if(root != null) stack.push(root);while(!stack.isEmpty()){TreeNode node = stack.peek();if(node != null){node = stack.pop();stack.push(node);stack.push(null);if(node.right != null) stack.push(node.right);if(node.left != null) stack.push(node.left);}else{stack.pop();node = stack.pop();list.add(node.val);}}return list;}
}
分析
- 可以看到使用空节点标记法,只需要修改两行代码就能写出不同的遍历代码
4、二叉树的层序遍历
学会二叉树的层序遍历,可以一口气打完以下十题:
- 102.二叉树的层序遍历
- 107.二叉树的层次遍历II
- 199.二叉树的右视图
- 637.二叉树的层平均值
- 429.N叉树的层序遍历
- 515.在每个树行中找最大值
- 116.填充每个节点的下一个右侧节点指针
- 117.填充每个节点的下一个右侧节点指针II
- 104.二叉树的最大深度
- 111.二叉树的最小深度
代码 102题
- 迭代
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> list = new ArrayList<>();if(root == null) return list;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while(!queue.isEmpty()){List<Integer> tempList = new ArrayList<>();int len = queue.size();while(len > 0){TreeNode node = queue.poll();tempList.add(node.val);if(node.left != null) queue.offer(node.left);if(node.right != null) queue.offer(node.right);len--;}list.add(tempList);}return list;}
}
- 递归
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> list = new ArrayList<>();level(root,list,0);return list;}public void level(TreeNode node,List<List<Integer>> list,int depth){if(node == null) return;depth++;if(list.size() < depth){List<Integer> tempList = new ArrayList<>();list.add(tempList);}list.get(depth-1).add(node.val);level(node.left,list,depth);level(node.right,list,depth);}
}
分析
- 迭代法借助了数据结构队列,先入先出。
226.翻转二叉树
leetcode链接

代码
- 前序遍历
class Solution {public TreeNode invertTree(TreeNode root) {preOrderReverse(root);return root;}public void preOrderReverse(TreeNode node){if(node == null) return;TreeNode temp = node.left;node.left = node.right;node.right = temp;preOrderReverse(node.left);preOrderReverse(node.right);}
}
- 后序遍历
class Solution {public TreeNode invertTree(TreeNode root) {preOrderReverse(root);return root;}public void preOrderReverse(TreeNode node){if(node == null) return;preOrderReverse(node.left);preOrderReverse(node.right);TreeNode temp = node.left;node.left = node.right;node.right = temp;}
}
- BFS
class Solution {public TreeNode invertTree(TreeNode root) {if(root == null) return root;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while(queue.size()>0){int size = queue.size();for(int i = 0;i < size;i++){TreeNode node = queue.poll();TreeNode temp = node.left;node.left = node.right;node.right = temp;if(node.left != null) queue.offer(node.left);if(node.right != null) queue.offer(node.right);}}return root;}
}
- 统一法
class Solution {public TreeNode invertTree(TreeNode root) {if(root == null) return root;Stack<TreeNode> stack = new Stack<>();stack.push(root);while(!stack.isEmpty()){TreeNode node = stack.peek();if(node != null){stack.pop();if(node.right != null) stack.push(node.right);if(node.left != null) stack.push(node.left);stack.push(node);stack.push(null);}else{stack.pop();node = stack.pop();TreeNode temp = node.left;node.left = node.right;node.right = temp;}}return root;}
}
分析
- 第一种递归的方式,只能写前序和后序,中序代码会导致有些节点反转了两次
- 第二种BFS,也就是层序遍历
- 第三种,统一的写法满足前中后序三种遍历方式
相关文章:

《代码随想录》--二叉树(一)
《代码随想录》--二叉树 第一部分 1、二叉树的递归遍历2、二叉树的迭代遍历3、统一风格的迭代遍历代码4、二叉树的层序遍历226.翻转二叉树 1、二叉树的递归遍历 前序遍历 中序遍历 后序遍历 代码 前序遍历 class Solution {public List<Integer> preorderTraversal(T…...
)
shell编程-数组与运算符详解(超详细)
文章目录 前言一、 Shell数组1. 声明和初始化数组2. 访问数组元素3. 数组长度4. 遍历数组5. 修改数组元素6. 删除数组元素7. 示例 二、Shell运算符1. 算术运算符1.1 加法运算符 ()1.2 减法运算符 (-)1.3 乘法运算符 (*)1.4 除法运算符 (/)1.5 取余运算符 (%) 2. 关系运算符2.1 …...
Vim入门
Vim使用入门 1.Vim编辑器的三种常用模式 一般模式:刚打开文件是它,从编辑模式按“ESC”退回的模式也是它。可以执行各种编辑操作,如移动光标、复制、粘贴、删除、查找替换等 ; 编辑模式:在一般模式下按下 i、I、a、A、o、O 等键…...

动态加载库
no_mangle 不要改标识符 首先是认识这个标注:mangle,英文的含义“撕裂、碾压”。我第一次把这个单次误以为是manage,说实话两个单词还挺像的。 RUS中函数或静态变量使用#[no_mangle]这个标注属性后,编译器就不会修改它们的名字了…...

React中渲染html结构---dangerouslySetInnerHTML
dangerouslySetInnerHTML胡子{}语法绑定的内容全部作为普通文本渲染,渲染html结构基于---dangerouslySetInnerHTMLdangerouslySetInnerHTML是React标签的一个属性,类似于vue的v-html有2个{{}},第一个{}代表jsx语法开始,第二个是代表dangerous…...
计网02-计算机网络参考模型
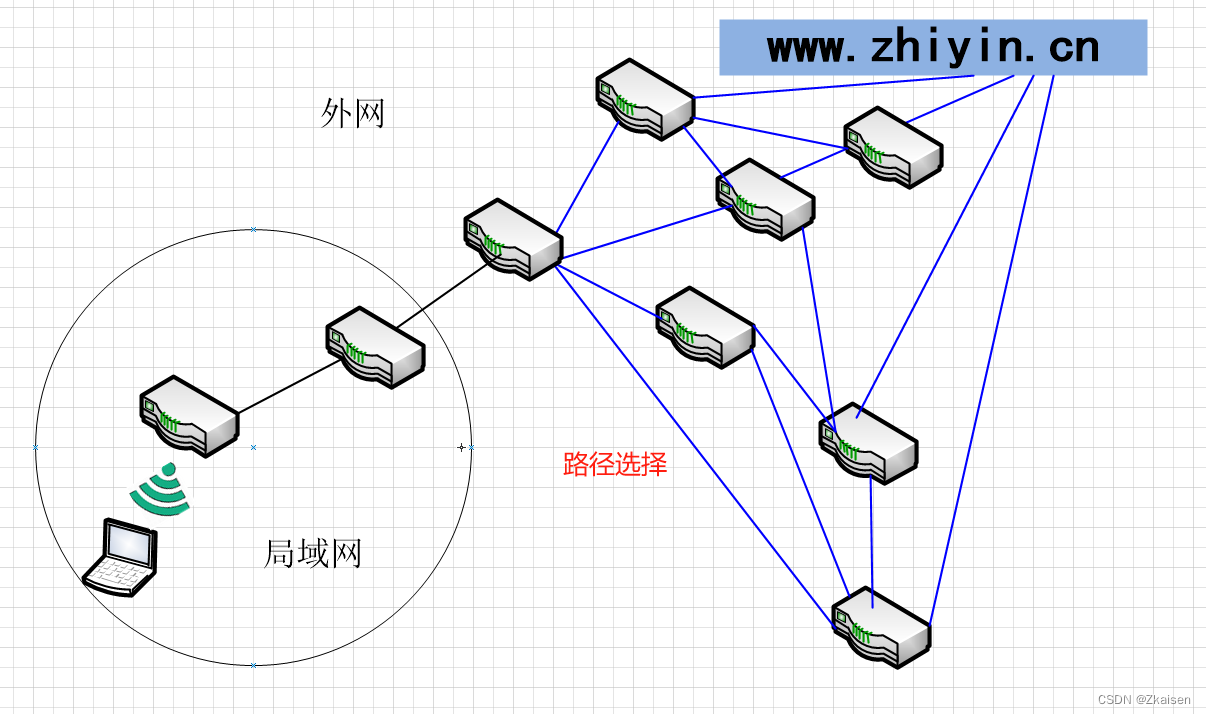
一、OSI七层参考模型 1、分层的思想 分层模型用于网络协议的设计方法,本质是将网络节点间复杂的通信问题分成若干简单的问题逐一解决,通过网络的层次去找问题,将复杂问题简单化。 2、OSI参考模型 由于早期计算机厂商使用的是私有的网络模…...

模块测试:确保软件质量的关键步骤
引言: 在软件开发过程中,模块测试是确保软件质量的关键环节。通过模块化的设计和测试方法,可以提高开发效率、降低错误率,并最终提供稳定可靠的软件产品。本文将介绍模块测试的概念、重要性以及实施步骤,帮助读者了解如…...

Postman接口测试之Postman常用的快捷键
作为一名IT程序猿,不懂一些工具的快捷方式,应该会被鄙视的吧。收集了一些Postman的快捷方式,大家一起动手操作~ 简单操作 xc 请求 操作MAC系统windows系统请求网址 ⌘L Ctrl L 保存请求 ⌘S Ctrl S 保存请求为 ⇧⌘S Ctrl Shift S发送…...

keil自动分配SDRAM空间设置使用
1.修改.sct文件 添加 RW_RAM1 0xC0400000 UNINIT 0x00400000 { ; RW data .ANY (SD_RAM1) 使用 #define LOCATION_ATTRIBUTE(name) __attribute__ ((section(name))) __attribute__ ((aligned(4)))uint8_t sdram_buf[0x100000] __attribute__ ((section("SD_RAM1")…...

TikTok获客怎么做?可以定制一个获客工具!
随着社交媒体的兴起,越来越多的企业开始将目光投向了短视频平台,TikTok作为其中的佼佼者,凭借其独特的算法和内容推荐机制,吸引了大量用户的关注。 那么,如何在TikTok上获取更多的客户呢?本文将为您揭秘TikTok获客的…...
数据结构(Chapter Two -02)—顺序表基本操作实现
在前一部分我们了解线性表和顺序表概念,如果有不清楚可以参考下面的博客: 数据结构(Chapter Two -01)—线性表及顺序表-CSDN博客 首先列出线性表的数据结构: #define MaxSize 50 //定义顺序表最大长度 typedef struct{ElemType data…...

SQL语句整理二--Mysql
文章目录 知识点梳理:1. mysql 中 in 和 exists 区别2. varchar 与 char 的区别 查看表结构:获取当前时间:查看建表语句:修改用户密码:查看所有用户:grant命令:判断当前数据库有多少连接数&…...
oracle与gbase8s迁移数据类型对照
声明:以下为笔者阅读gbase官方文档和oracle官方文档的理解,如有错误,敬请指正。oracle与gbase8s迁移数据类型对照及举例说明 最终结论:oracle与gbase8s数据类型对应关系关于单精度与双精度的区别关于定点与浮点定义的区别精度的定…...

Flink系列之:集合操作
Flink系列之:集合操作 一、集合操作二、UNION三、INTERSECT四、EXCEPT五、IN六、EXISTS 一、集合操作 适用于流、批操作 二、UNION UNION 和 UNION ALL 返回两个表中的数据。 UNION 会去重,UNION ALL 不会去重。 Flink SQL> create view t1(s) as…...

STL:string的常见用法
目录 赋值和连接: operator: 赋值操作符: assign(str): 将字符串赋值为另一个字符串: : 字符串连接操作符: 访问和检查: at(pos): 返回指定位置的字符,提供边界检查。 operator[]: 返回指定位置的字符…...

GBASE南大通用 ADO.NET 中的事务
GBASE南大通用 ADO.NET 中支持事务,可以使用GBASE南大通用Connection 对象的BeginTransaction 函数开始一个事务,并默认使用 ReadCommitted 模式初始化。 事务中可以对单个表执行多个操作,或者对多个表执行多个操作,在事务未提交…...

App(Android)ICP备案号查询——————高仿微信
😄 个人主页:✨拉莫帅-CSDN博客✨🤔 博文:132篇🔥 原创:130篇,转载:2篇🔥 总阅读量:388923❤️ 粉丝量:112🍁 感谢点赞和关注 &#x…...
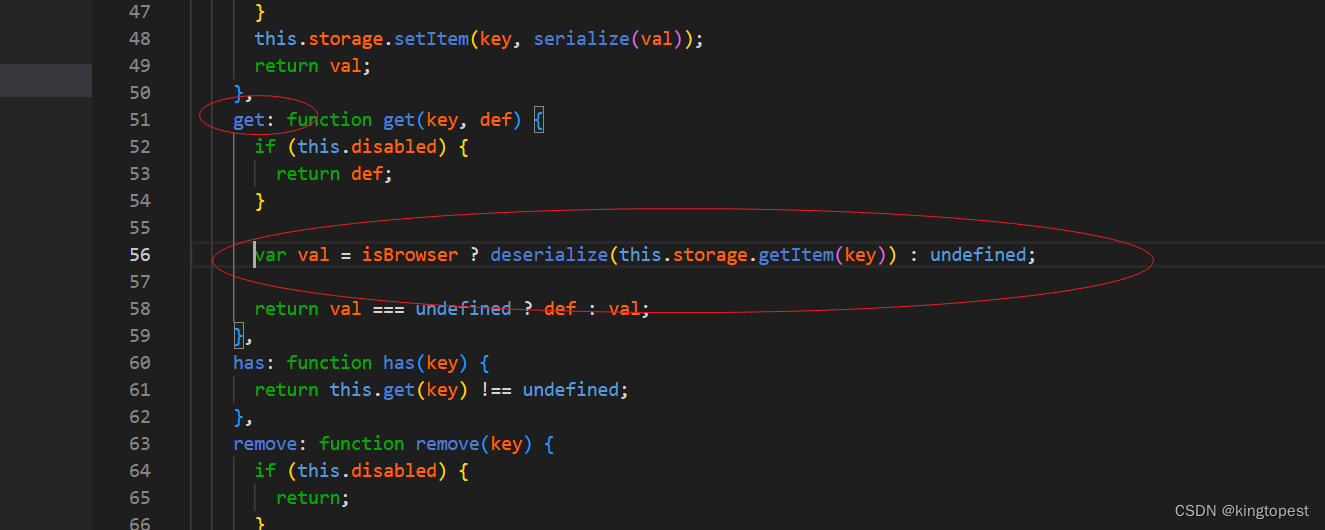
修改npm源码解决服务端渲染环境中localstorage报错read properties of undefined (reading getItem)
现象: 这个问题是直接指向了我使用的第三方库good-storage,这是一个对localStorage/sessionStorage做了简单封装的库,因为项目代码有一个缓存cache.ts有用到 原因分析: 从表象上看是storage对象找不到getItem方法, 但…...

Educational Codeforces Round 160 (Div. 2) A~C(D,E更新中...)
A.Rating Increase(思维) 题意: 给出一个仅包含数字的字符串 s s s,要求将该字符串按以下要求分成左右两部分 a , b a,b a,b: 两个数字均不包含前导 0 0 0 两个数字均大于 0 0 0 b > a b > a b>a 如果…...

【Maven-Helper】利用 Maven-Helper 解决依赖冲突问题
【Maven-Helper】利用 Maven-Helper 解决依赖冲突问题 1)安装 Maven-Helper 插件2)Maven Helper 插件使用方法3)Idea-Maven 可视化依赖树 1)安装 Maven-Helper 插件 这里我们已经安装过了,如果没有安装过,点…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
