非递归实现的快速排序
目录
序列文章
前言
学前补充
非递归快速排序
注意事项(重要)
实现步骤
代码实现
时空复杂度
快速排序的特性
栈的相关代码
序列文章
非递归实现的快速排序:http://t.csdnimg.cn/UEcL6
快速排序的挖坑法与双指针法:http://t.csdnimg.cn/I1L7Q
快速排序的hoare法:http://t.csdnimg.cn/SV0nA
前言
一般来说,我们在写排序时都比较喜欢使用递归的方式,但是递归如果层次太深可能会引起栈溢出的问题,所以我们在本篇会讲解如何使用非递归的方式实现快速排序\( ̄︶ ̄*\))
学前补充
对于递归改非递归我们其实已经不是第一次写了,比如斐波那契数列中的递归改非递归:
//递归实现斐波那契数列
#include <stdio.h>
int count = 0;
int Fid(int n)
{if (n <= 0)return 0;else if (n == 1)return 1;elsecount++;return Fid(n - 1) + Fid(n - 2);}int main()
{int n = 0;printf("请输入要求第几个斐波那契数列中的数字:>");scanf_s("%d", &n);int ret = Fid(n);printf("该数字为:%d\n", ret);printf("需要计算的次数为: %d\n", count);return 0;
}//迭代(循环)实现斐波那契数列
#include <stdio.h>
int count = 0;
int Fun(int n)
{int a = 1;int b = 1;int c = 1;while (n > 2) //当n>2时开始进行循环相加{c = a + b;a = b;b = c;count++;n--;}return c; //当n<2时直接输出1}int main()
{int n = 0;printf("请输入要求第几个斐波那契数列中的数字:>");scanf_s("%d", &n);int num = Fun(n);printf("该数字为:%d\n", num);printf("所需要的次数为:%d",count);return 0;
}
我们会发现,可以实现递归改迭代的问题,它们使用迭代实现的思路会比递归更加的好理解,所以一般来说我们在进行递归改非递归的过程中,会将递归改为迭代的形式。
但是对于快速排序而言,我们会利用栈来将它改为非递归的方式而不是迭代,这是因为在快速排序中,每次划分操作会将原始数组划分为两个较小的子数组。然后我们需要对这两个子数组进行进一步的划分和排序。这种嵌套关系导致了一个逻辑上的函数调用链。
使用循环来实现非递归版本时,我们无法直接模拟出函数调用链中各级函数之间传递参数和保存局部变量等信息的机制。而通过使用栈数据结构,在每次遇到新的待处理子数组时,我们可以将相关信息(如起始索引、结束索引)压入栈中,并在下一轮迭代时从栈中弹出并取出相应信息进行处理。
换句话说,通过利用栈作为辅助数据结构,在代码层面上模拟了逻辑上函数调用链所需传递和保存状态信息等功能。这样就能够以迭代方式按照特定顺序处理所有待处理子问题(即待切割和排序的子数组),达到完成整体排序任务。
结论:在非递归实现快速排序算法时选择使用栈来管理状态信息是一种常见且有效的策略
非递归快速排序
注意事项(重要)
我们利用栈存储的是每次要进行排序的数组元素的下标的值,而不是该数组元素的值,我们会将这些下标代入到之前实现过的单趟的快速排序中(比如伪双指针法快速排序),每次循环都进行一次单趟排序,这样就可以不再像递归那样排序时,需要借助栈帧
实现步骤
1、将数组首尾元素下标0和9入栈,将栈顶元素分别赋值给变量left和right后,栈顶元素出栈(赋值一个出一个,一共四步:入->出->入->出)将作left和right传入快速排序(其实就是begin和end)实现单趟排序
2、将单趟排序后形成的左区间和右区间的四个下标值入栈(单趟排序返回的是作为分界线元素的下标的值)


3、后续入栈出栈过程不予解释建议自行理解
代码实现
//非递归排序
void QuickSortNonR(int* a, int begin, int end)
{//初始化栈ST s;STInit(&s);//将数组首尾元素的下标的值作为x入栈STPush(&s, end);STPush(&s, begin);//栈不为空就循环while (!STEmpty(&s)){//获取栈顶元素值(原数组中的下标),并让栈顶元素出栈(获取完此时的栈顶元素就出,获取两个栈顶元素就开始排序)int left = STTop(&s);STPop(&s);int right = STTop(&s);STPop(&s);//将获取的两个下标值进行单趟排序(利用之前的伪双指针法)int keyi = PartSort3(a, left, right);// [left, keyi-1] keyi [keyi+1, right]//当左区间范围不为1时(没法继续缩小问题规模),将划分后左区间两个边界位置元素的下标值入栈if (left < keyi - 1){STPush(&s, keyi - 1);STPush(&s, left);}//当右区间范围不为1时(没法继续缩小问题规模),将划分后右区间两个边界位置元素的下标值入栈 if (keyi + 1 < right){STPush(&s, right);STPush(&s, keyi + 1);}}//最后销毁栈空间STDestroy(&s);
}时空复杂度
最坏时间复杂度:O(N^2)(当输入数组完全有序时,每次切分操作都可能将数组分为一个较小的部分和一个较大的部分,导致每次切分只能减少一项)
最好时间复杂度:O(N*logN)(每次划分都能将数组均匀地分成两个接近子数组,N个元素要进行logN次的排序,N*logN,跟前面的递归排序的意思差不多)
空间复杂度:O(logN)(不需要额外的栈空间来保存状态信息,只需维护一个辅助堆栈用于存储待处理子数组的起止索引即可)
快速排序的特性
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 稳定性:不稳定
栈的相关代码
代码太多,就不再全部展示了,需要的自提:http://t.csdnimg.cn/kheGO
~over~
相关文章:
非递归实现的快速排序
目录 序列文章 前言 学前补充 非递归快速排序 注意事项(重要) 实现步骤 代码实现 时空复杂度 快速排序的特性 栈的相关代码 序列文章 非递归实现的快速排序:http://t.csdnimg.cn/UEcL6 快速排序的挖坑法与双指针法:ht…...
windows 安装jenkins
下载jenkins 官方下载地址:Jenkins 的安装和设置 清华源下载地址:https://mirrors.tuna.tsinghua.edu.cn/jenkins/windows-stable/ 最新支持java8的版本时2.346.1版本,在清华源中找不到,在官网中没找到windows的下载历史ÿ…...
SQL进阶理论篇(十二):InnoDB中的MVCC是如何实现的?
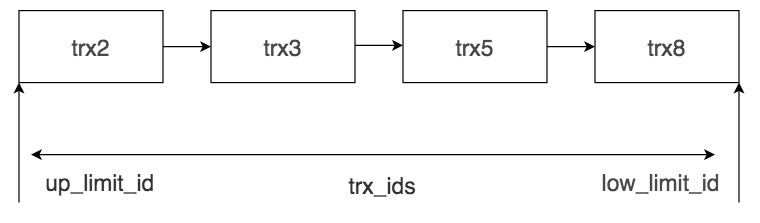
文章目录 简介事务版本号行记录的隐藏列Undo LogRead View的工作流程总结参考文献 简介 在不同的DBMS里,MVCC的实现机制是不同的。本节我们会以InnoDB举例,讲解InnoDB里MVCC的实现机制。 我们需要掌握这么几个概念: 事务版本号行记录的隐藏…...

SpringCloudAliBaba篇之Seata:分布式事务组件理论与实践
1、事务简介 事务(Transaction)是访问并可能更新数据库中各种数据项的一个程序执行单元(unit)。在关系数据库中,一个事务由一组SQL语句组成,事务具有4个属性:原子性、一致性、隔离性、持久性。这四个属性通常称为ACID原则。 原子性(atomici…...
在centos7.9上安装Jenkins的安装过程
1.jenkins的安装和配置: 安装JDK: yum install -y fontconfig java-11-openjdk # 安装目录:/usr/lib/jvm # fontconfig 是 Linux 系统中用于配置和管理字体的一种工具 下载jenkins安装包: sudo wget -O /etc/yum.repos.d/jenkins…...

uni-app基本标签
导航栏设置 - navigationBarBackgroundColor: 设置导航栏的背景颜色(全局页面) - navigationBarTextStyle: 导航栏标题颜色(仅支持 black 和 white) - navigationBarTitleText: 设置导航栏标题内容 - enablePullDownRefresh: 是否…...

《PySpark大数据分析实战》-14.云服务模式Databricks介绍基本概念
📋 博主简介 💖 作者简介:大家好,我是wux_labs。😜 热衷于各种主流技术,热爱数据科学、机器学习、云计算、人工智能。 通过了TiDB数据库专员(PCTA)、TiDB数据库专家(PCTP…...
微信小程序校园跑腿系统怎么做,如何做,要做多久
在这个互联网快速发展、信息爆炸的时代,人人都离不开手机,每个人都忙于各种各样的事情,大学生也一样,有忙于学习,忙于考研,忙着赚学分,忙于参加社团,当然也有忙于打游戏的&#x…...
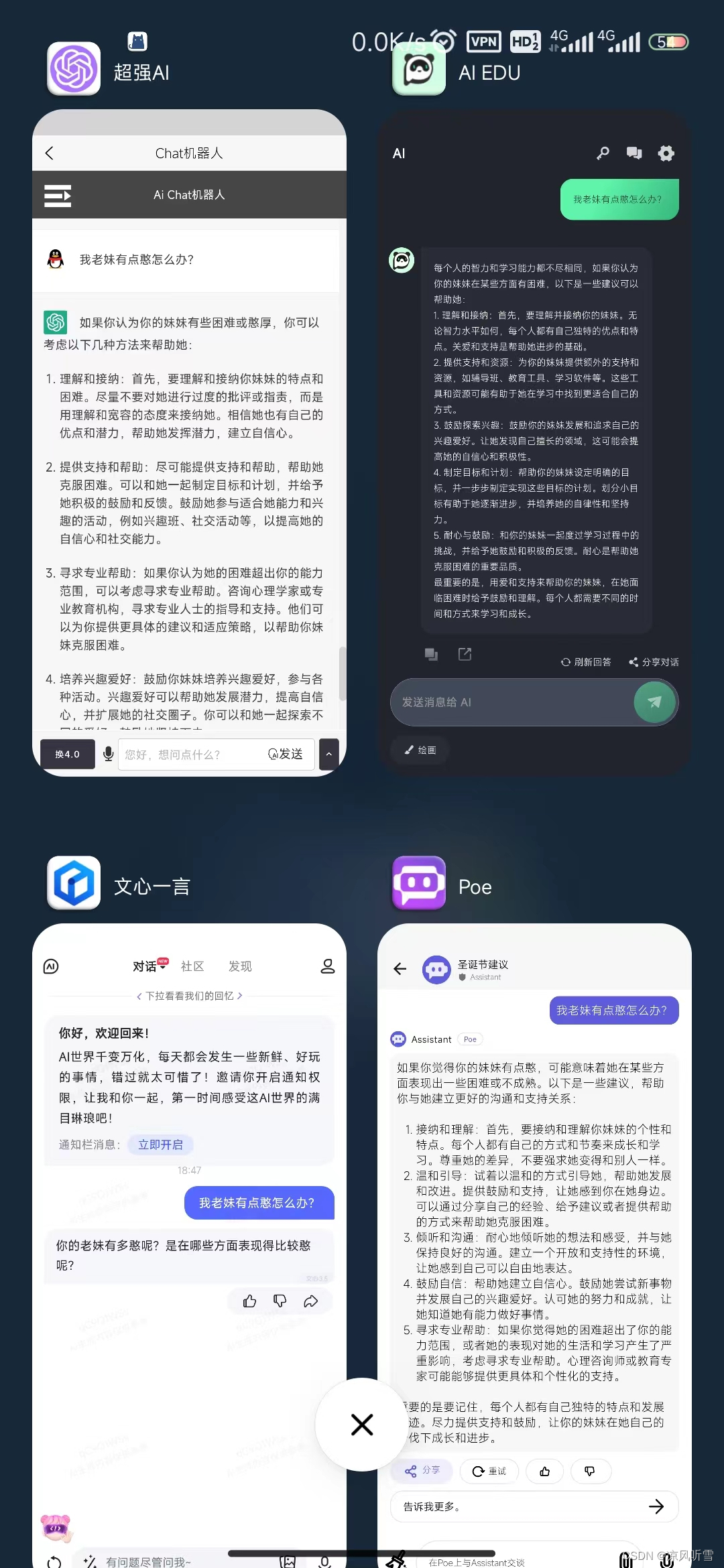
当我分别问8款GPT一个问题。。。
前两天下班在地铁上无聊寻思问一下不同的GPT一个相同的问题,哪个会给出我比较满意的答案,然后我就提问:我老妹有点憨怎么办?(ps:开玩笑的,嘻嘻。。。) 很明显其他GPT都给出了大差不差…...

Elasticsearch 8.9 search命令执行查询源码
一、相关的API的handler1、接收HTTP请求的handler2、往数据节点发送查询请求的action(TransportSearchAction)3、通过transportService把查询请求发送到指定的数据节点 二、数据节点收到请求的处理逻辑1、尝试从缓存中加载查询结果2、不通过缓存查询,直接执行查询(1…...

【PHP】身份证正则验证、校验位验证
目录 1.正则 简单正则 详细正则 2.校验位验证 1.正则 简单正则 function isValidIdCardNumber($idCardNumber) {// 身份证号长度为 15 位或 18 位$pattern /^(?:\d{15}|\d{17}[\dxX])$/;return preg_match($pattern, $idCardNumber); }$idCardNumber 12345678901234567…...
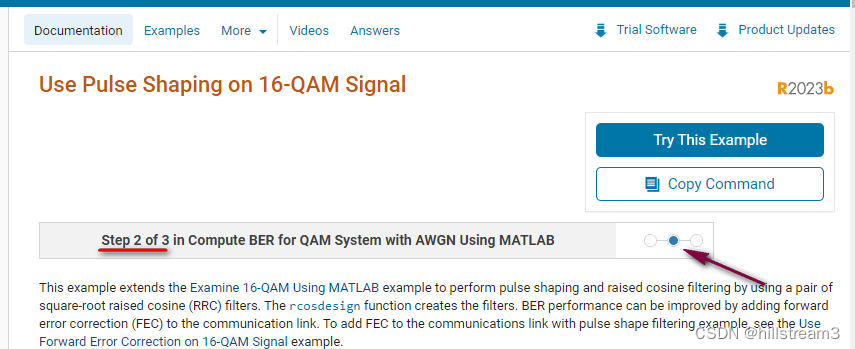
Matlab示例-Examine 16-QAM Using MATLAB学习笔记
工作之余学习16-QAM 写在前面 网上看到许多示例,但一般都比较难以跑通。所以,还是老方法,先将matlab自带的例子研究下。 Examine 16-QAM Using MATLAB Examine 16-QAM Using MATLAB 或者,在matlab中,键入&#x…...

ArcGIS Pro SDK运行消息只提示一次
工具大部分都是异步执行,所以提示信息需要异步执行完再进行,所以注意async和await的使用。 相关async和await的文章请查看C# 彻底搞懂async/await_c# async await-CSDN博客 public async Task InformationPrompt() {string message String.Empty;await ArcGIS.De…...
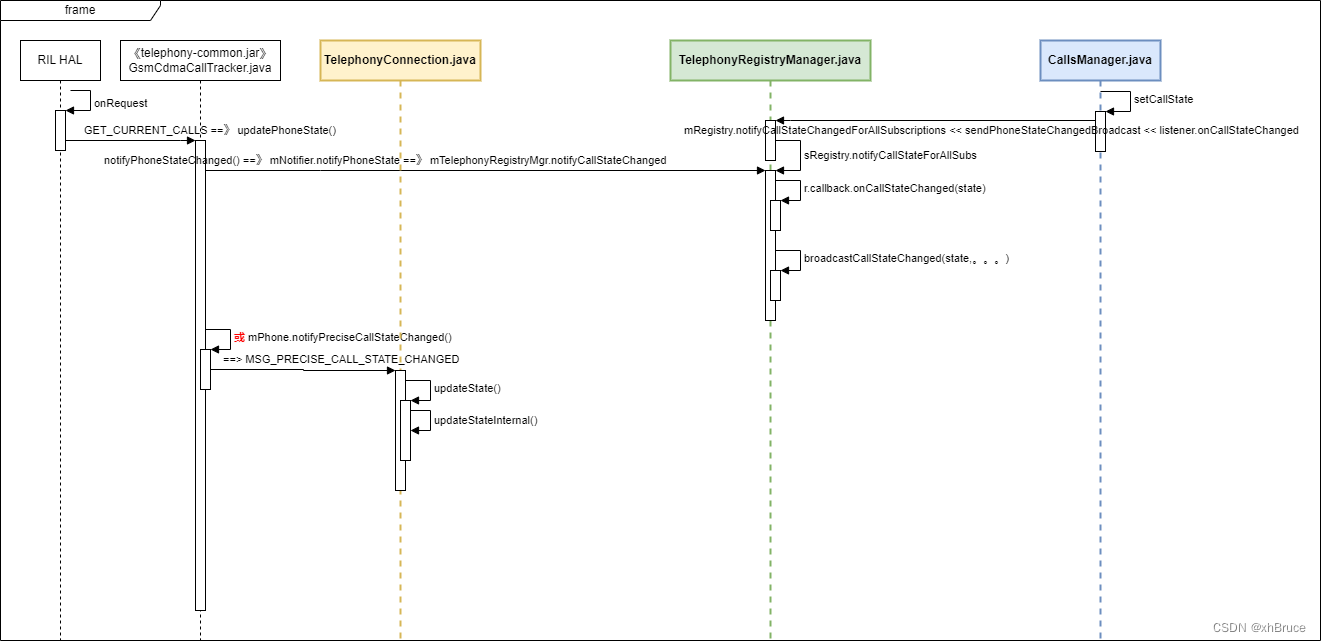
通话状态监听-Android13
通话状态监听-Android13 1、Android Telephony 模块结构2、监听和广播获取通话状态2.1 注册2.2 通话状态通知2.3 通话状态 3、通知状态流程* 关键日志 frameworks/base/core/java/android/telephony/PhoneStateListener.java 1、Android Telephony 模块结构 Android Telephony…...
无懈可击的防泄密之旅:迅软DSE在民营银行的成功实践
客户简要介绍 某股份有限公司主体是中部地区的民营银行,由其母公司联合9家知名民营企业共同发起设立。正式开业于2016年,紧紧围绕目标产业生态圈和消费金融,着力打造产业银行、便捷银行、数字银行、财富管理银行为一体的BEST银行,…...

【送书活动】智能汽车、自动驾驶、车联网的发展趋势和关键技术
文章目录 前言01 《智能汽车》推荐语 02 《SoC底层软件低功耗系统设计与实现》推荐语 03 《SoC设计指南》推荐语 05 《智能汽车网络安全权威指南(上册)》推荐语 06 《智能汽车网络安全权威指南(下册)》推荐语 后记赠书活动 前言 …...

不同版本QT使用qmake时创建QML项目的区别
不同版本QT使用qmake时创建QML项目的区别 文章目录 不同版本QT使用qmake时创建QML项目的区别一、QT5新建QML项目1.1 目录结构1.2 .pro 文件内容1.3 main.cpp1.4 main.qml 二、QT6新建QML项目2.1 目录结构2.2 .pro文件内容2.3 main.cpp2.4 main.qml 三、两个版本使用资源文件的区…...
【PHP入门】1.1-PHP初步语法
-PHP语法初步- PHP是一种运行在服务器端的脚本语言,可以嵌入到HTML中。 1.1.1PHP代码标记 在PHP历史发展中,可以使用多种标记来区分PHP脚本 ASP标记: <% php代码 %>短标记: <? Php代码 ?>,以上两种…...
如何在jenkins容器中安装python+httprunner+pytest+git+allure(一)
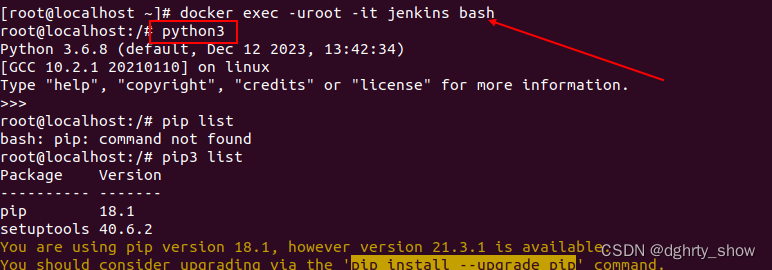
背景: API接口自动化使用python语言实现,利用httprunner框架编写自动化用例场景(执行的时候还是依赖pytest),使用jenkins自动构建git上的源代码,并产生allure报告可视化展示API执行结果。 步骤 1.进入jenkins容器 注意使用roo…...

Android终端模拟器Termux上使用Ubuntu
Termux 上安装各种 Linux 系统是通过 proot-distro 工具来实现的,所以先安装一下 proot-distro 工具。 ~ $ pkg install proot-distro 查看Termux支持安装那些Linux ~ $ proot-distro listSupported distributions:* Alpine LinuxAlias: alpineInstalled: noComme…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

