距离矩阵路径优化Python Dijkstra(迪杰斯特拉)算法和冲突驱动子句学习
Dijkstra算法
Dijkstra 算法是一种流行的寻路算法,通常用于基于图的问题,例如在地图上查找两个城市之间的最短路径、确定送货卡车可能采取的最短路径,甚至创建游戏地图。其背后的直觉基于以下原则:从起始顶点访问所有相邻顶点,同时跟踪迄今为止距起始顶点的最小距离。 该算法按以下步骤运行:
- 创建一个数组,用于保存每个顶点与起始顶点的距离。最初,将所有顶点的距离设置为无穷大,起始顶点除外,起始顶点应设置为 0。
- 创建一个优先级队列(堆)并插入距离为0的起始顶点。
- 当优先级队列中仍有顶点时,选择距起始顶点记录距离最小的顶点并访问其相邻顶点。
- 对于每个相邻顶点,检查它是否已经被访问过。 如果尚未访问过,则通过将其权重添加到迄今为止为其父级找到的最小距离来计算其暂定距离
- 如果这个暂定距离小于之前记录的值(如果有),请在我们的“distances”数组中更新它。
- 最后,将这个访问过的顶点及其更新的距离添加到我们的优先级队列中,并重复步骤 3,直到我们到达目的地或耗尽所有节点。
通过迭代所有相邻节点,我们可以确保我们已经探索了每条可能的路径,以确定哪条路径的总成本(距离)最短。 我们使用优先级队列数据结构来有效地跟踪接下来需要访问哪些节点,而不是在每次迭代中扫描每个节点。
通过以这种方式跟踪距离并迭代邻居,我们最终可以找到从起始节点(或更确切地说距离[源])到图中其他节点/城市的所需最小路径。
这就是 Dijkstra 算法背后的基本直觉!通过迭代地执行这些步骤,我们最终将找出从源顶点开始的图中任意顶点的最短距离。现在让我们用 Python 编写代码。
Python实现算法
def min_distance(distances, visited):min_val = float('inf')min_index = -1for i in range(len(distances)):if distances[i] < min_val and i not in visited:min_val = distances[i]min_index = ireturn min_indexdef dijkstra_algorithm(graph, start_node):num_nodes = len(graph)distances = [float('inf')] * num_nodesvisited = []distances[start_node] = 0for i in range(num_nodes):current_node = min_distance(distances, visited)visited.append(current_node)for j in range(num_nodes):if graph[current_node][j] != 0:new_distance = distances[current_node] + graph[current_node][j]if new_distance < distances[j]:distances[j] = new_distancereturn distances
以下是如何通过示例图使用此函数:
# 2D array
graph = [[0, 7, 9, 0, 0, 14],[7, 0, 10, 15, 0, 0],[9, 10, 0, 11, 0, 2],[0, 15, 11, 0, 6, 0],[0, 0, 0, 6, 0 ,9],[14. 0 ,2 ,0 ,9 ,8 ,10]]shortest_distances = dijkstra_algorithm(graph, 'A')print(shortest_distances)
[0.00... # Distance from start node to itself is zero
7
9
20
20
12
]
这演示了如何将 Dijkstra 算法与 Python 结合使用来查找图中的最短路径。
Python可视化 Dijkstra算法
开放街道地图(OSM)
Python Dijkstra算法寻找最短路径
冲突驱动子句学习
- 预处理:计算距离矩阵
- 创建网络图
- 使用 NetworkX 计算最短路径
- 使用 Plotly 动画生成模拟
- 使用 OR-Tools 解决旅行商问题(简单的路线优化)
- 使用 OR-Tools 解决车辆路径问题(高级路径优化)
参阅一 - 亚图跨际
参阅二 - 亚图跨际
相关文章:
算法和冲突驱动子句学习)
距离矩阵路径优化Python Dijkstra(迪杰斯特拉)算法和冲突驱动子句学习
Dijkstra算法 Dijkstra 算法是一种流行的寻路算法,通常用于基于图的问题,例如在地图上查找两个城市之间的最短路径、确定送货卡车可能采取的最短路径,甚至创建游戏地图。其背后的直觉基于以下原则:从起始顶点访问所有相邻顶点&am…...
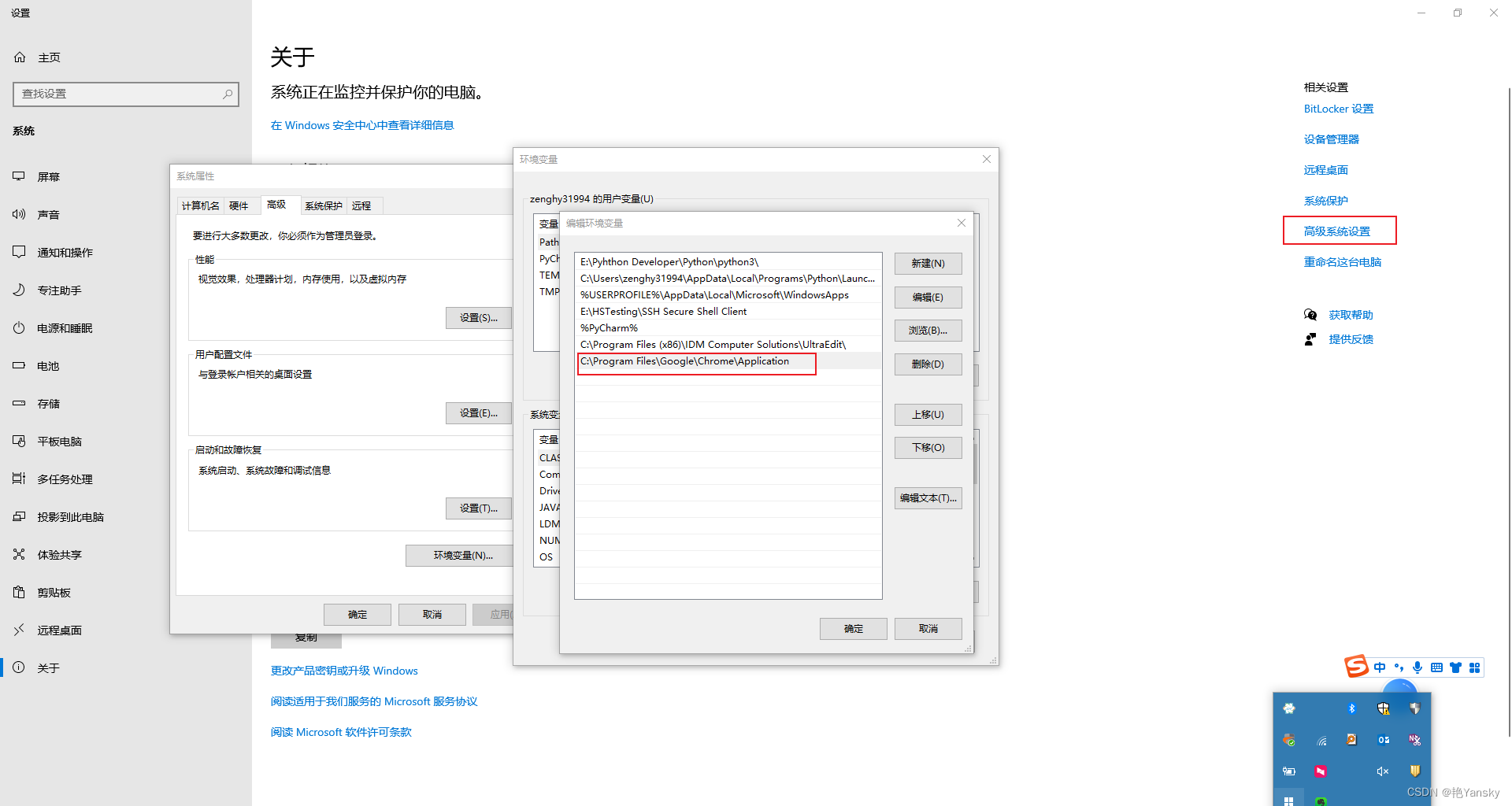
Selenium安装WebDriver:ChromeDriver与谷歌浏览器版本快速匹配_最新版120
最近在使用通过selenium操作Chrome浏览器时,安装中遇到了Chrome版本与浏览器驱动不匹配的的问题,在此记录安装下过程,如何快速找到与谷歌浏览器相匹配的ChromeDriver驱动版本。 1. 确定Chrome版本 我们首先确定自己的Chrome版本 Chrome设置…...
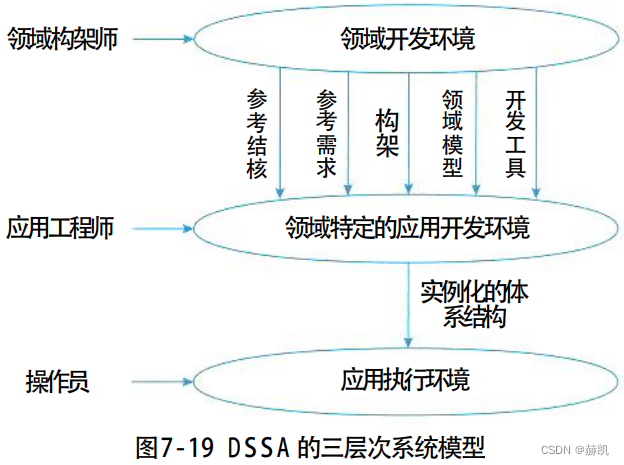
系统架构设计师教程(七)系统架构设计基础知识
系统架构设计基础知识 7.1 软件架构概念7.1.1 软件架构的定义7.1.2 软件架构设计与生命周期需求分析阶段设计阶段实现阶段构件组装阶段部署阶段后开发阶段 7.1.3 软件架构的重要性 7.2 基于架构的软件开发方法7.2.1 体系结构的设计方法概述7.2.2 概念与术语7.2.3 基于体系结构的…...
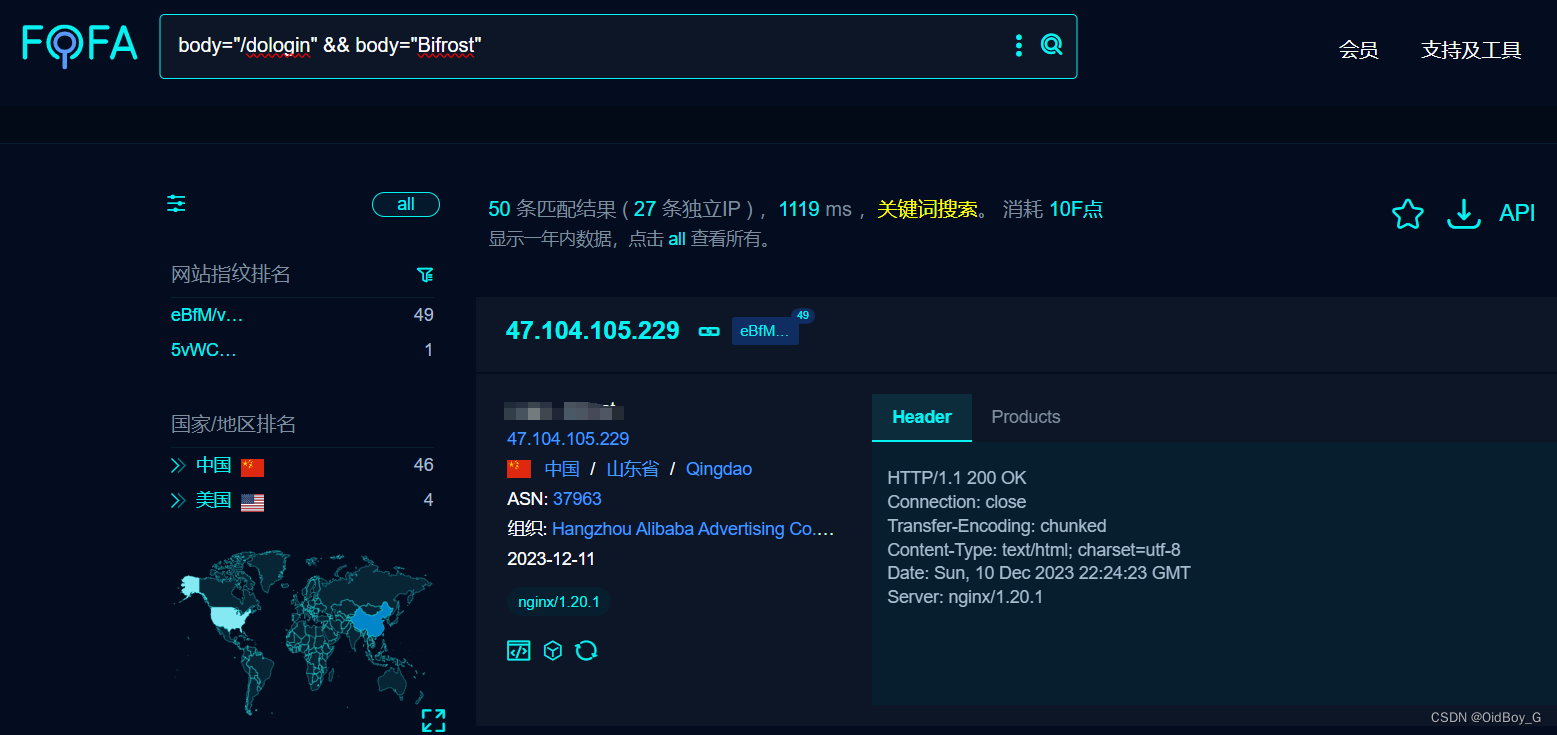
Bifrost 中间件 X-Requested-With 系统身份认证绕过漏洞复现
0x01 产品简介 Bifrost是一款面向生产环境的 MySQL,MariaDB,kafka 同步到Redis,MongoDB,ClickHouse等服务的异构中间件 0x02 漏洞概述 Bifrost 中间件 X-Requested-With 存在身份认证绕过漏洞,未经身份认证的攻击者可未授权创建管理员权限账号,可通过删除请求头实现身…...

OpenSSL 3.2.0新增Argon2支持——防GPU暴力攻击
1. 引言 OpenSSL新发布的3.20版本中,引入了一些新特性,包括: post-quantum方法Brainpool曲线QUICArgon2:Argon2 是一种慢哈希函数,在 2015 年获得 Password Hashing Competition 冠军,利用大量内存计算抵…...

数据结构--稀疏矩阵及Java实现
一、稀疏 sparsearray 数组 1、先看一个实际的需求 编写的五子棋程序中,有存盘退出和续上盘的功能。 分析问题: 因为该二维数组的很多值是默认值 0, 因此记录了很多没有意义的数据.->稀疏数组。 2、稀疏数组基本介绍 当一个数组中大部分元素为0…...
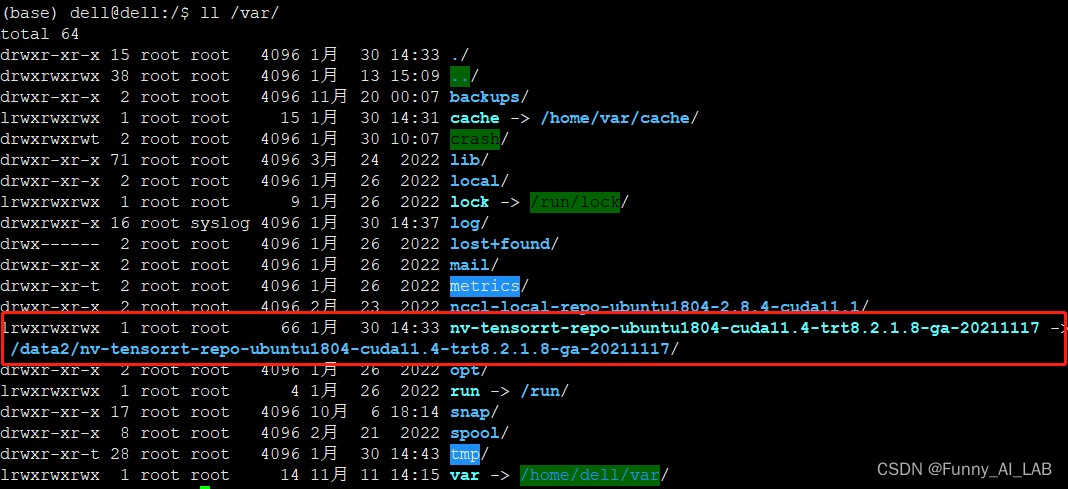
关于GPU使用过程中的若干问题
1.CUDA异常 问题描述:运行torch.cuda.is_available() 报错:cuda unknown error - this may be due to an incorrectly set up environment解决方案:重启 2.nvidia驱动版本不匹配 问题描述:运行nvidis-smi 报错:Fa…...
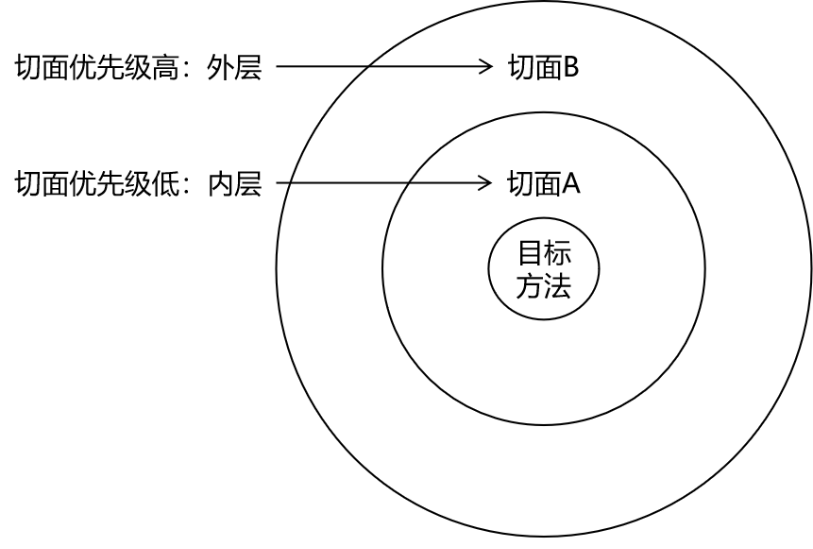
spring之面向切面:AOP(2)
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持,想组团高效学习… 想写博客但无从下手,急需…...

【开题报告】基于uniapp的家庭记账小程序的设计与实现
1.研究背景 随着社会经济的发展和人们生活水平的提高,家庭财务管理变得越来越重要。家庭记账是一种重要的财务管理方式,通过记录和分析家庭的收入和支出情况,可以帮助家庭成员更好地理解和掌握自己的财务状况,合理规划和管理家庭…...

HTML5面试题
HTML5面试题 什么是HTML5?它与HTML4有何不同之处? HTML5是HTML的第五个主要版本,它引入了许多新的语义化元素、API和功能,以改进网页的结构、样式、交互和多媒体体验。 HTML5与HTML4的不同之处包括: 引入了一系列新的语…...

树莓派通过网线连接电脑并且设置设置链接wifi
好久没玩过树莓派了,系统进不去了,需要记录一下,之前总觉得自己会了,但是还是需要不断的翻阅资料。 树莓派 配置SD卡开启ssh - 哔哩哔哩 树莓派通过网线连接ssh 直接在sd卡建立一个ssh的文件,不要带任何后戳 ip查…...

C#拼接JSON
一、业务背景 最近项目需要与U8c对接,实现增删改查,借此机会,梳理一下C#解析Json字符串的问题。 这篇文章,先以新增接口为例。 二、新增接口 查看需要传入的json格式。 拼接json,无非就是{}和[]的来回嵌套。 首先&am…...

评价机器学习模型的指标
为了衡量一个机器学习模型的好坏,需要给定一个测试集,用模型对测试集中的每一个样本进行预测,并根据预测结果计算评价分数。 对于分类问题,常见的评价标准有准确率、精确率、召回率和F值等。给定测试集 𝒯 {(…...
C# WPF上位机开发(日志调试)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 程序开发的过程中,调试肯定是少不了的。比如说,这个时候,我们可以设置断点、查看变量、检查函数调用堆栈等等。…...

AR室内导航如何实现?技术与原理分析
随着科技的进步,我们生活中许多方面正在被重新定义。其中之一就是导航,尤其是室内导航。增强现实(AR)技术的出现为室内导航带来了革命性的变革。本文将深入探讨AR室内导航的技术与原理,以及它如何改变我们的生活方式。…...

计算机网络:物理层(奈氏准则和香农定理,含例题)
带你速通计算机网络期末 文章目录 一、码元和带宽 1、什么是码元 2、数字通信系统数据传输速率的两种表示方法 2.1、码元传输速率 2.2、信息传输速率 3、例题 3.1、例题1 3.2、例题2 4、带宽 二、奈氏准则(奈奎斯特定理) 1、奈氏准则简介 2、…...

天津仁爱学院专升本化学工程与工艺专业 《无机化学》考试大纲
天津仁爱学院化学工程与工艺专业高职升本入学考试《无机化学》课程考试大纲 一.参考教材 杨宏孝《无机化学简明教程》以及《无机化学简明教程学习指南》,高等教育出版社,2011年版。 二.考试基本要求 本考试要求将《无机化学》…...
GO 的 socks5代理 编写
这里学习一下 socks5 代理的编写 网上有很多 学习一下 go 语言实战入门案例之实现Socks5 - 知乎 滑动验证页面 socks5协议原理学习-腾讯云开发者社区-腾讯云 (tencent.com) 首先我们要了解一下socks5的代理方式 socks5 是基于 认证建立连接转发数据 所形成的代理 我们只…...

MYSQL-简单的联表查询示例
假设我们有两个表,一个是users表,包含用户的ID和姓名;另一个是orders表,包含订单的ID、用户ID和订单金额。我们想要关联这两个表,查询出每个用户的订单总金额。 首先,我们可以使用以下SQL查询获取每个用户…...

Python基于joblib的并行计算进程线程multiprocessing多核并行计算
文章目录 Python基于joblib的并行计算适用场景使用示例总结爬虫&joblib使用`joblib`的场景注意事项使用实例结论joblib介绍简单示例多参数并行并行时CPU是怎么分配的何时选用并行进程&线程进程和线程之间的关系...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
