算法学习——回溯算法
回溯算法
- 理论基础
- 回溯法的效率
- 回溯法解决的问题
- 回溯法模板
- 组合
- 思路
- 回溯法三部曲
- 代码
- 组合(优化)
- 组合总和III
- 思路
- 代码
- 电话号码的字母组合
- 思路
- 回溯法来解决n个for循环的问题
- 回溯三部曲
- 代码
- 组合总和
- 思路
- 代码
- 组合总和II
- 思路
- 代码
理论基础
什么是回溯法?
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。
在二叉树系列中,我们已经不止一次,提到了回溯,例如二叉树:以为使用了递归,其实还隐藏着回溯。
回溯是递归的副产品,只要有递归就会有回溯。
所以以下讲解中,回溯函数也就是递归函数,指的都是一个函数。
回溯法的效率
回溯法的性能如何呢,这里要和大家说清楚了,虽然回溯法很难,很不好理解,但是回溯法并不是什么高效的算法。
因为回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是穷举的本质。
那么既然回溯法并不高效为什么还要用它呢?
因为没得选,一些问题能暴力搜出来就不错了,撑死了再剪枝一下,还没有更高效的解法。
那么都什么问题,这么牛逼,只能暴力搜索。
回溯法解决的问题
回溯法,一般可以解决如下几种问题:
组合问题:N个数里面按一定规则找出k个数的集合
切割问题:一个字符串按一定规则有几种切割方式
子集问题:一个N个数的集合里有多少符合条件的子集
排列问题:N个数按一定规则全排列,有几种排列方式
棋盘问题:N皇后,解数独等等
回溯法模板
卡哥总结的回溯算法模板。
回溯三部曲:
1.回溯函数模板返回值以及参数:回溯算法中函数返回值一般为void。再来看一下参数,因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来,所以一般是先写逻辑,然后需要什么参数,就填什么参数。
回溯函数伪代码如下:
void backtracking(参数)
2.回溯函数终止条件:
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
所以回溯函数终止条件伪代码如下:
if (终止条件) {存放结果;return;
}
3.回溯搜索的遍历过程:
在上面我们提到了,回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。
回溯函数遍历过程伪代码如下:
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果
}
for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
组合
力扣题目链接
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
思路
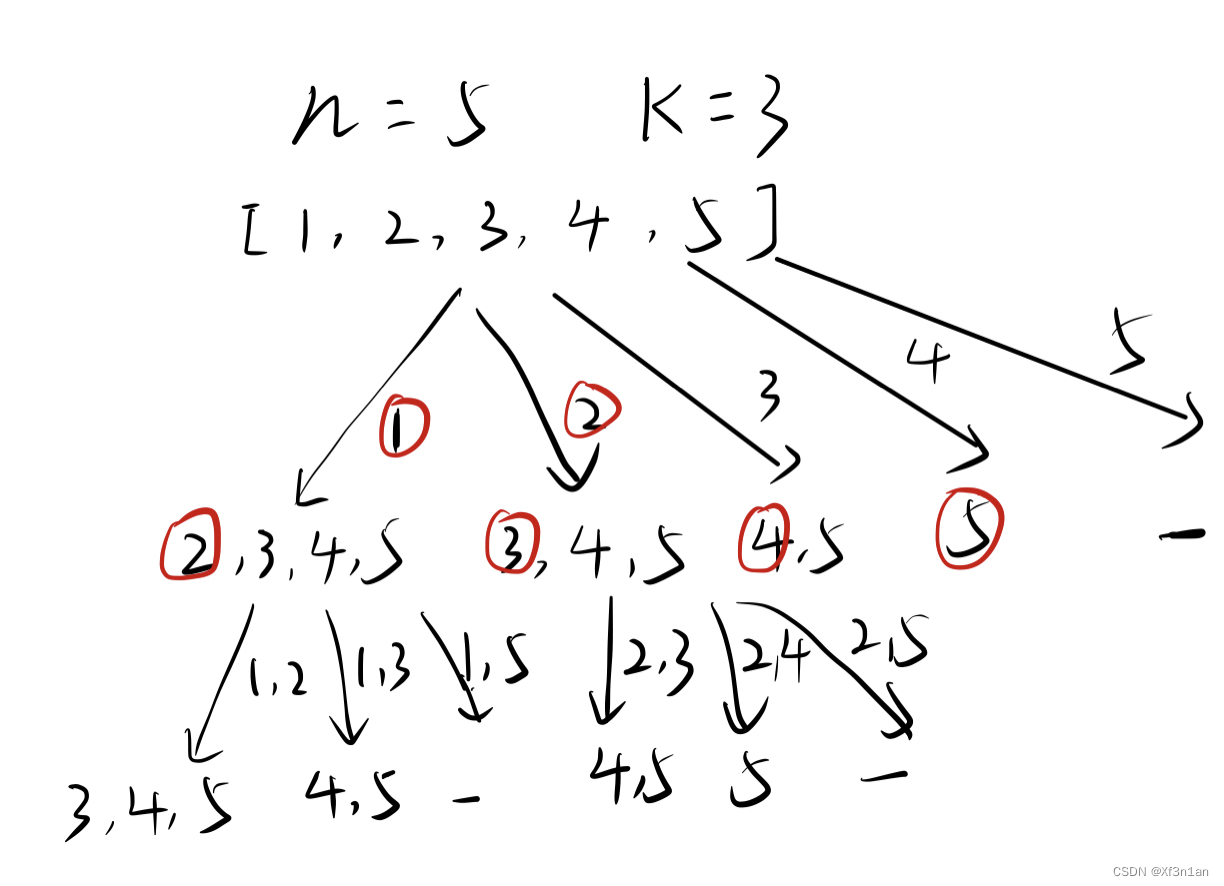
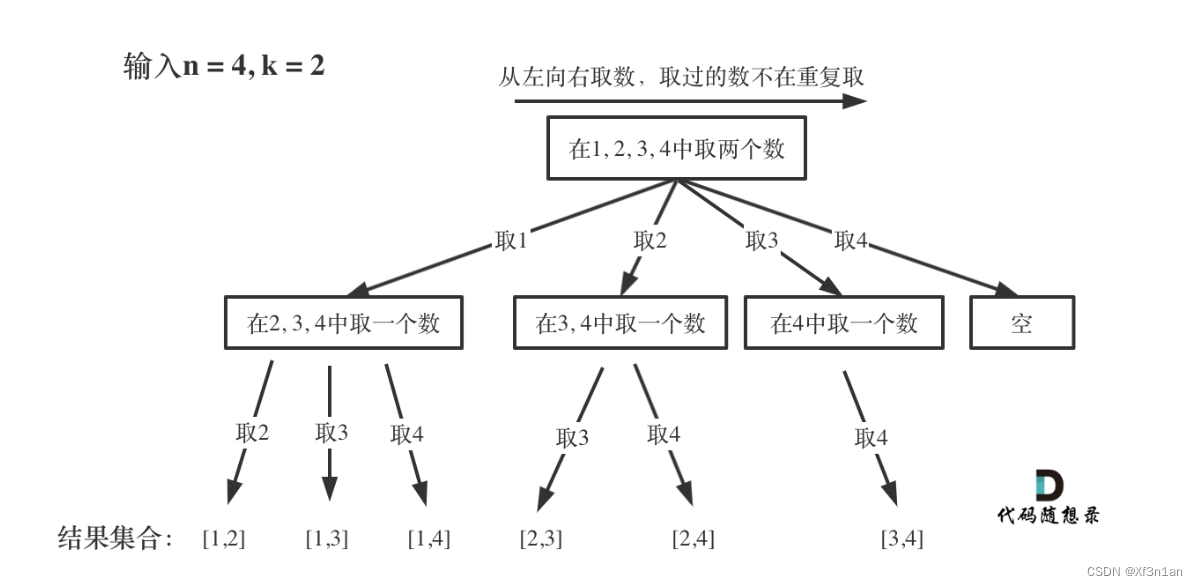
可以看出这棵树,一开始集合是 1,2,3,4, 从左向右取数,取过的数,不再重复取。
第一次取1,集合变为2,3,4 ,因为k为2,我们只需要再取一个数就可以了,分别取2,3,4,得到集合[1,2] [1,3] [1,4],以此类推。
每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围。
图中可以发现n相当于树的宽度,k相当于树的深度。
那么如何在这个树上遍历,然后收集到我们要的结果集呢?
图中每次搜索到了叶子节点,我们就找到了一个结果。
相当于只需要把达到叶子节点的结果收集起来,就可以求得 n个数中k个数的组合集合。
回溯法三部曲
递归函数的返回值以及参数
在这里要定义两个全局变量,一个用来存放符合条件单一结果,一个用来存放符合条件结果的集合。
vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件结果
函数里一定有两个参数,既然是集合n里面取k个数,那么n和k是两个int型的参数。
然后还需要一个参数,为int型变量startIndex,这个参数用来记录本层递归中,集合从哪里开始遍历(集合就是[1,…,n] )。
为什么要有这个startIndex呢?
startIndex 就是防止出现重复的组合。
从下图中红线部分可以看出,在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIndex。
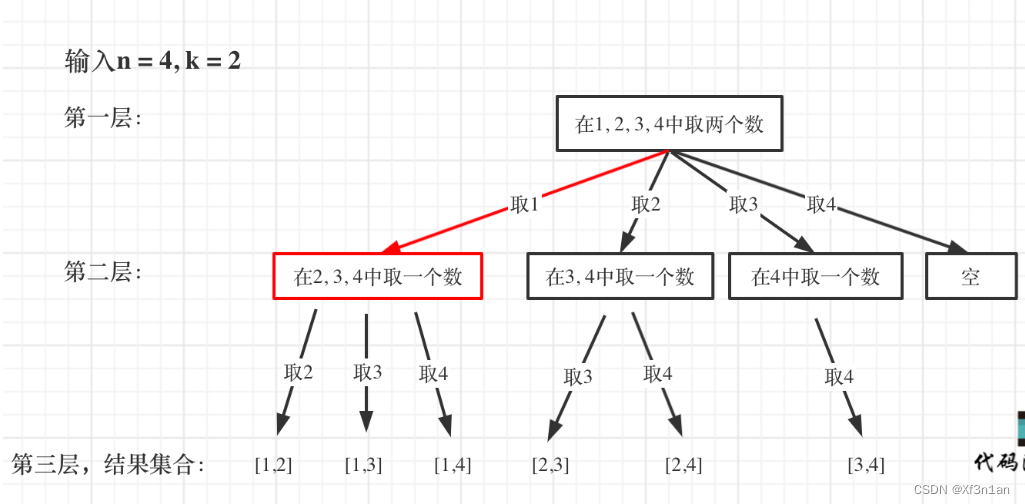
所以需要startIndex来记录下一层递归,搜索的起始位置。
那么整体代码如下:
vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件单一结果
void backtracking(int n, int k, int startIndex)
回溯函数终止条件
什么时候到达所谓的叶子节点了呢?
path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合了,在图中path存的就是根节点到叶子节点的路径。
此时用result二维数组,把path保存起来,并终止本层递归。
所以终止条件代码如下:
if (path.size() == k) {result.push_back(path);return;
}
单层搜索的过程
回溯法的搜索过程就是一个树型结构的遍历过程,在如下图中,可以看出for循环用来横向遍历,递归的过程是纵向遍历。
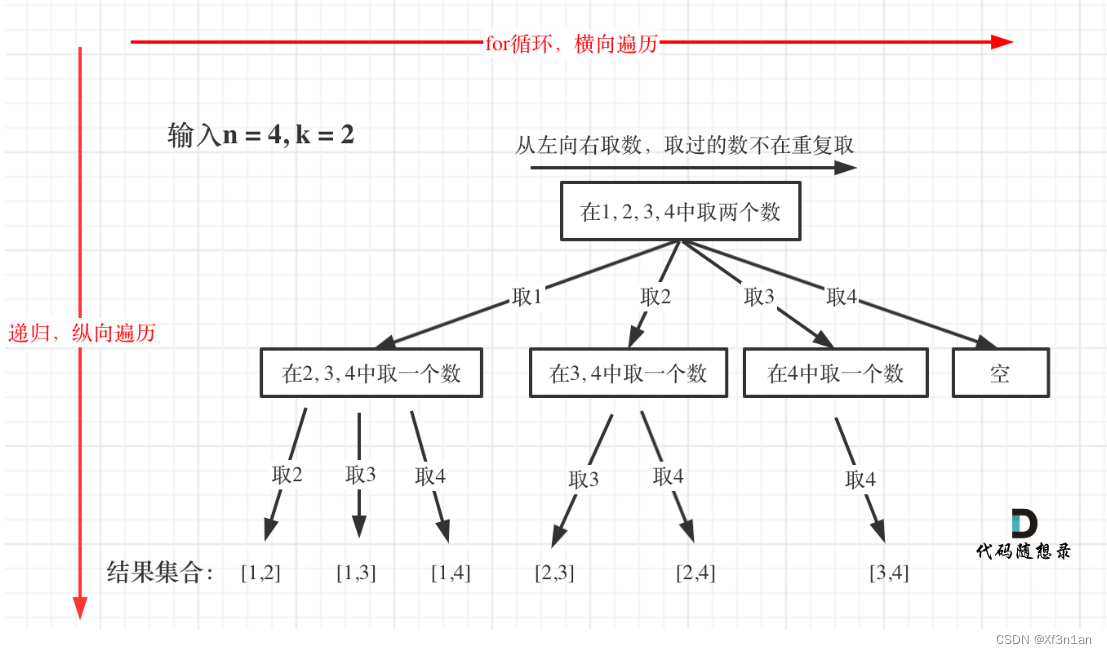
如此我们才遍历完图中的这棵树。
for循环每次从startIndex开始遍历,然后用path保存取到的节点i。
可以看出backtracking(递归函数)通过不断调用自己一直往深处遍历,总会遇到叶子节点,遇到了叶子节点就要返回。
backtracking的下面部分就是回溯的操作了,撤销本次处理的结果。
代码如下:
for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历path.push_back(i); // 处理节点backtracking(n, k, i + 1); // 递归:控制树的纵向遍历,注意下一层搜索要从i+1开始path.pop_back(); // 回溯,撤销处理的节点
}
代码
class Solution {
public:vector<int> paths;vector<vector<int>>result;void backtracking(int n , int k ,int startidx){if(paths.size()==k){result.push_back(paths);return;} for(int i = startidx;i <= n ;i++){paths.push_back(i);backtracking(n,k,i+1);paths.pop_back();}}vector<vector<int>> combine(int n, int k) {backtracking(n,k,1);return result;}
};
组合(优化)
组合总和III
力扣题目链接
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
所有数字都是正整数。
解集不能包含重复的组合。
示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]
思路
代码
class Solution {
public:vector<vector<int>>result;vector<int>paths;int sum = 0;void backtracking(int n , int k,int startidx){if(paths.size()>k) return;if(sum > n) return;if(paths.size()==k && sum==n ){result.push_back(paths);return ;}for(int i = startidx; i<=9;++i){paths.push_back(i);sum+=i;backtracking(n,k,i+1);paths.pop_back();sum-=i;}}vector<vector<int>> combinationSum3(int k, int n) {backtracking(n,k,1);return result;}
};
电话号码的字母组合
力扣题目链接
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 :
输入:digits = “23”
输出:[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]
思路
数字和字母如何映射
可以使用map或者定义一个二维数组,例如:string letterMap[10],来做映射,我这里定义一个二维数组,代码如下:
const string letterMap[10] = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz", // 9
};
回溯法来解决n个for循环的问题
例如:输入:“23”,抽象为树形结构,如图所示:
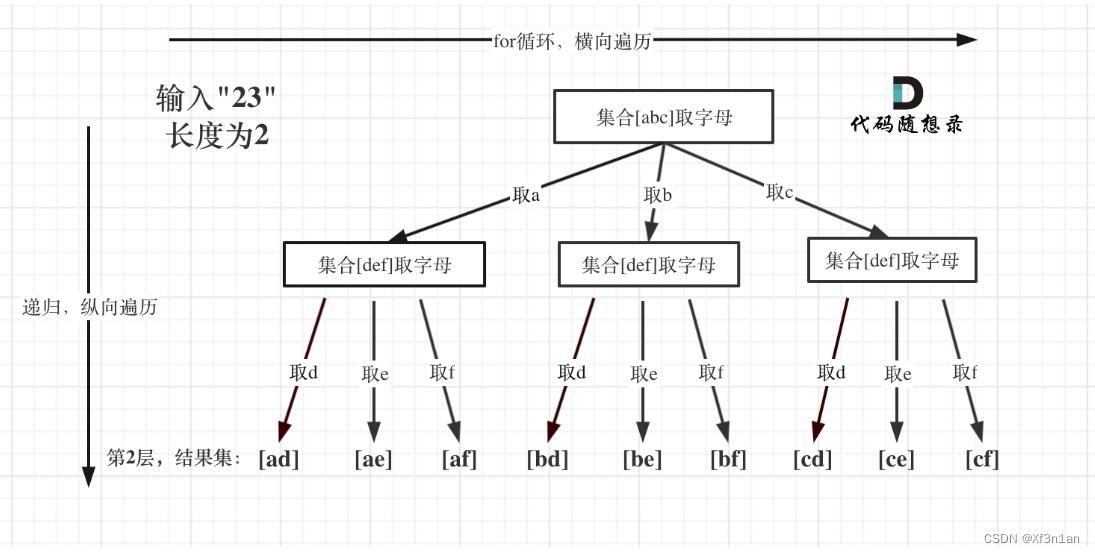
图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”]。
回溯三部曲
确定回溯函数参数
首先需要一个字符串s来收集叶子节点的结果,然后用一个字符串数组result保存起来,这两个变量我依然定义为全局。
再来看参数,参数指定是有题目中给的string digits,然后还要有一个参数就是int型的index。
这个index是记录遍历第几个数字了,就是用来遍历digits的(题目中给出数字字符串),同时index也表示树的深度。
代码如下:
vector<string> result;
string s;
void backtracking(const string& digits, int index)
确定终止条件
例如输入用例"23",两个数字,那么根节点往下递归两层就可以了,叶子节点就是要收集的结果集。
那么终止条件就是如果index 等于 输入的数字个数(digits.size)了(本来index就是用来遍历digits的)。
然后收集结果,结束本层递归。
代码如下:
if (index == digits.size()) {result.push_back(s);return;
}
这里index跳出循环后的大小就是数组的大小
确定单层遍历逻辑
首先要取index指向的数字,并找到对应的字符集(手机键盘的字符集)。
然后for循环来处理这个字符集,代码如下:
int digit = digits[index] - '0'; // 将index指向的数字转为int
string letters = letterMap[digit]; // 取数字对应的字符集
for (int i = 0; i < letters.size(); i++) {s.push_back(letters[i]); // 处理backtracking(digits, index + 1); // 递归,注意index+1,一下层要处理下一个数字了s.pop_back(); // 回溯
}
注意这里for循环,可不像是在回溯算法:求组合问题和回溯算法:求组合总和中从startIndex开始遍历的。
因为本题每一个数字代表的是不同集合,也就是求不同集合之间的组合,而上述两道题都是求同一个集合中的组合!
代码
class Solution {
public:const vector<string>phones = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};vector<string>result;string path;void backtracking(string digits , int index){if( index == digits.size()){result.push_back(path);return;}int num = digits[index] - '0';string words = phones[num];for(int i = 0 ; i < words.size();++i){path.push_back(words[i]);backtracking(digits,index+1);path.pop_back();}}vector<string> letterCombinations(string digits) {if(digits.size()==0)return result;backtracking(digits,0);return result;}
};
组合总和
力扣题目链接
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为: [ [7], [2,2,3] ]
思路
代码
class Solution {
public:vector<vector<int>>result;vector<int>paths;void backtracking(vector<int>& candidates , int target ,int sum , int startidx){if(sum > target){return;}if(sum == target){result.push_back(paths);return ;}for(int i = startidx ; i < candidates.size();++i){paths.push_back(candidates[i]);sum += candidates[i];backtracking(candidates,target,sum,i);sum -= candidates[i];paths.pop_back();}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {backtracking(candidates,target,0,0);return result;}
};
组合总和II
力扣题目链接
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明: 所有数字(包括目标数)都是正整数。解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[[1, 7],[1, 2, 5],[2, 6],[1, 1, 6]
]
思路
如果 candidates 中有重复元素,可能会生成重复的组合。为了避免这种情况,首先需要对 candidates 进行排序。排序后,相同的数字会排列在一起,从而可以更容易地跳过重复的组合。
不排序去重:

代码
class Solution {
public:vector<vector<int>>result;vector<int>path;void backtracking(vector<int>& candidates, int target, int sum,int startidx ){if(sum > target)return;if(sum==target){result.push_back(path);return;}for(int i = startidx;i<candidates.size();++i){if(i>startidx && candidates[i]==candidates[i-1])continue;path.push_back(candidates[i]);sum += candidates[i];backtracking(candidates,target,sum,i+1);sum -= candidates[i];path.pop_back();}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());backtracking(candidates,target,0,0);return result;}
};
相关文章:

算法学习——回溯算法
回溯算法 理论基础回溯法的效率回溯法解决的问题回溯法模板 组合思路回溯法三部曲 代码 组合(优化)组合总和III思路代码 电话号码的字母组合思路回溯法来解决n个for循环的问题回溯三部曲代码 组合总和思路代码 组合总和II思路代码 理论基础 什么是回溯法…...
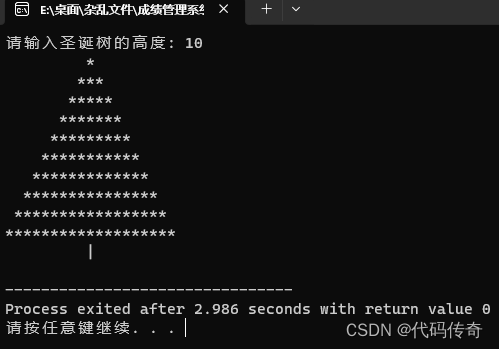
C语言—小小圣诞树
这个代码会询问用户输入圣诞树的高度,然后根据输入的高度在控制台上显示相应高度的圣诞树。 #include <stdio.h>int main() {int height, spaces, stars;printf("请输入圣诞树的高度: ");scanf("%d", &height);spaces height - 1;st…...

Android消息公告上下滚动切换轮播实现
自定义控件 通过继承TextSwitcher实现 直接上代码 public class NoticesSwitcher extends TextSwitcher implements ViewSwitcher.ViewFactory {private Context mContext;private List<Notice> mData;private final long DEFAULT_TIME_SWITCH_INTERVAL 1000;//1spri…...
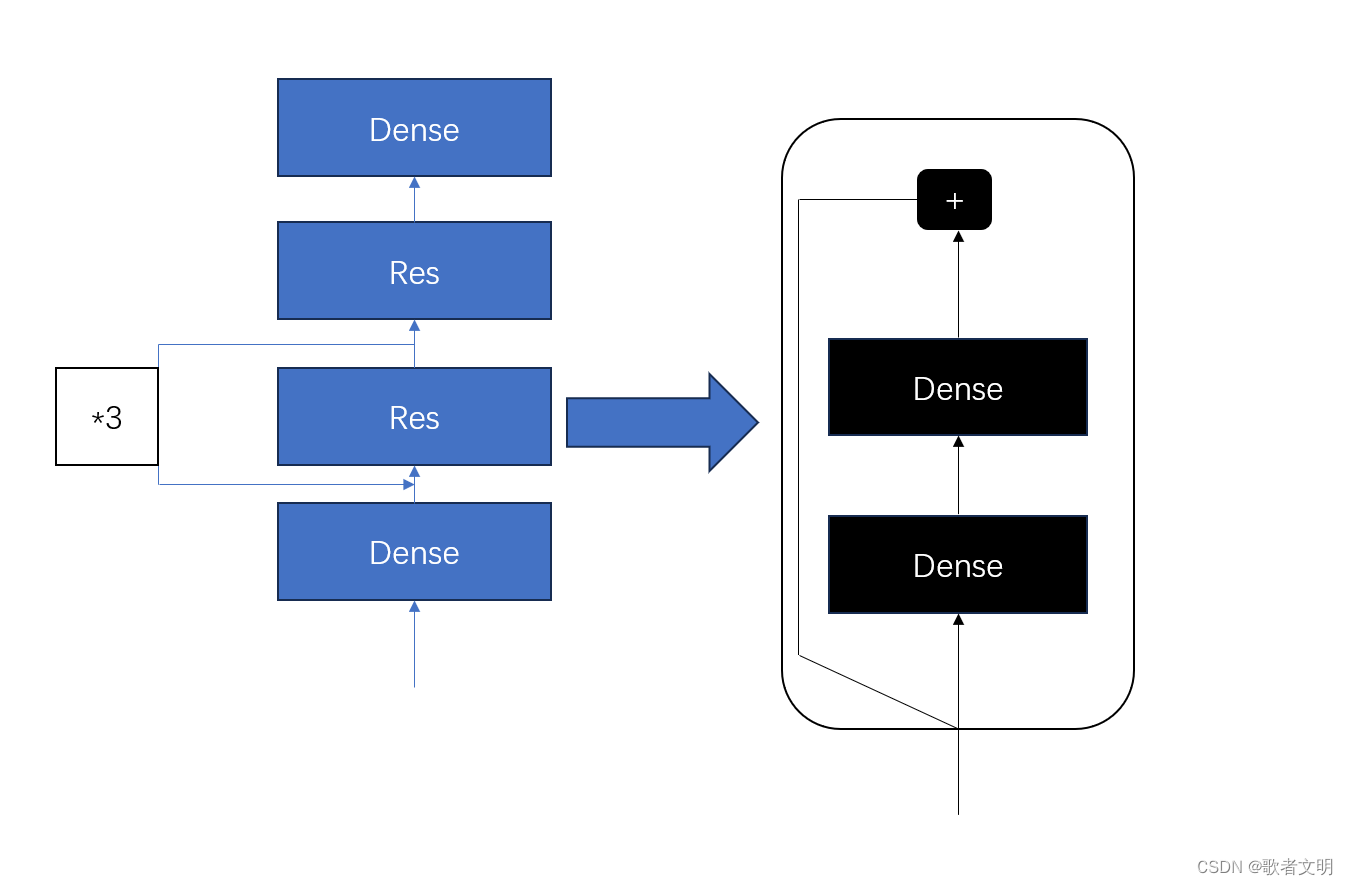
tensorflow入门 自定义模型
前面说了自定义的层,接下来自定义模型,我们以下图为例子 这个模型没啥意义,单纯是为了写代码实现这个模型 首先呢,我们看有几个部分,dense不需要我们实现了,我们就实现Res,为了实现那个*3,我们…...
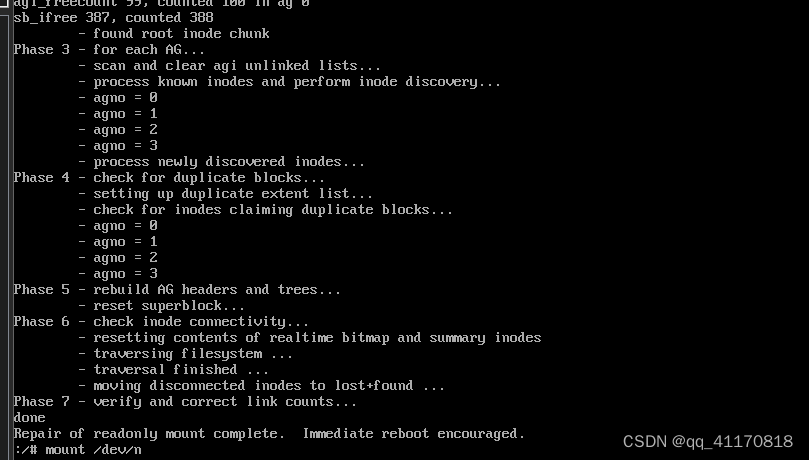
虚拟机启动 I/O error in “xfs_read_agi+0x95“
1.在选择系统界面按e 进入维护模式 2.找到ro把ro改成 rw init/sysroot/bin/sh 然后按Ctrlx 3.找到坏掉的分区,以nvme0n1p3为例进行修复 xfs_repair -d /dev/nvme0n1p3 4.init 6 重新启动 以下情况 先umount 再修复 则修复成功...

【MYSQL】-库的操作
💖作者:小树苗渴望变成参天大树🎈 🎉作者宣言:认真写好每一篇博客💤 🎊作者gitee:gitee✨ 💞作者专栏:C语言,数据结构初阶,Linux,C 动态规划算法🎄 如 果 你 …...

网络协议小记
一、TCP/IP协议 作为一个小萌新,当然我无法将tcp/ip协议的大部分江山和盘托出,但是其中很多面试可能问到的知识,我觉得有必要总结一下! 首先,在学习tcp/ip协议之前,我们必须搞明白什么是tcp/ip协议。 1、…...

STM32-I2C通讯-AHT20温湿度检测
非常感谢,提供的视频学习 https://www.bilibili.com/video/BV1QN411D7ak/?spm_id_from333.788&vd_source8ca4826038edd44bb618801808a5e076 该文章注意:串口显示中文会乱码,必须选用支持ASCII的串口助手,才能正常显示中文。…...
【机器学习】043_准确率、精确率、召回率
一、定义 在处理偏斜数据集时,通常使用不同的误差度量,而不仅仅是使用分类误差来衡量算法性能。 1. 混淆矩阵的概念 二分类问题的混淆矩阵为2X2矩阵,由四部分组成: 假阴性(FN):模型预测为负…...

【Qt开发流程】之文件目录、文件、输入和输出
概述 应用程序操作过程中,经常要对设备或文件进行读或者写操作。也会经常对文件及目录进行操作。 在Qt中,QIODevice类是Qt中所有进行I/O操作的设备的基类,比如QFile、 QIODevice为支持数据块读写的设备(如QFile、QBuffer和QTcpSo…...

CSS的基本选择器及高级选择器(附详细示例以及效果图)
Hi i,m JinXiang ⭐ 前言 ⭐ 本篇文章主要介绍HTML中CSS的基础选择及高级选择器(详解)以及部分理论知识 🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁 🍉博主收将持续更新学习记录获…...
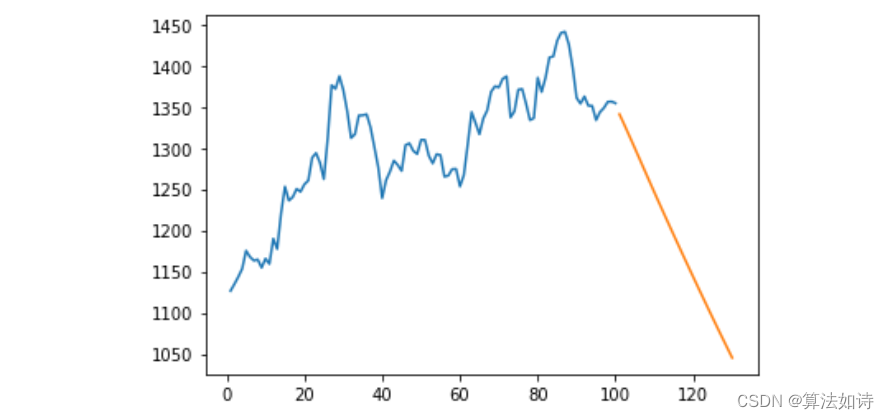
股票价格预测 | Python实现基于Stacked-LSTM的股票预测模型,可预测未来(keras)
文章目录 效果一览文章概述模型描述源码设计效果一览 文章概述 以股票价格预测为例,基于Stacked-LSTM的股票预测模型(keras),可预测未来。 模型描述 LSTM 用于处理序列数据,如时间序列、文本和音频。相对于传统的RNN,LSTM更擅长捕获长期依赖关系,...
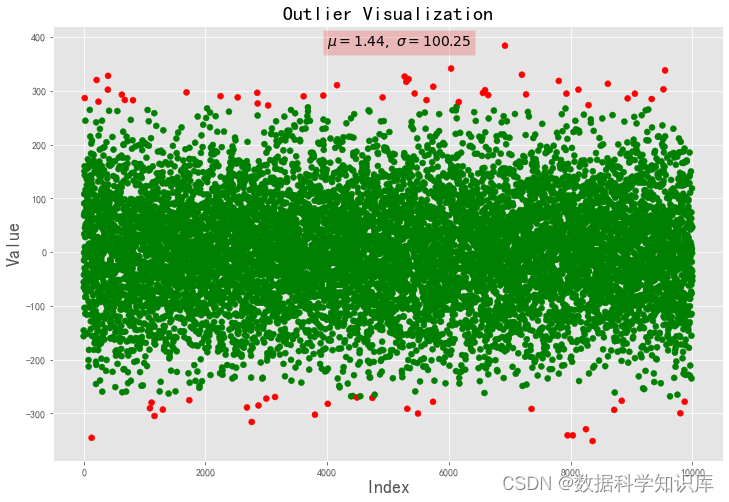
数据可视化---离群值展示
内容导航 类别内容导航机器学习机器学习算法应用场景与评价指标机器学习算法—分类机器学习算法—回归机器学习算法—聚类机器学习算法—异常检测机器学习算法—时间序列数据可视化数据可视化—折线图数据可视化—箱线图数据可视化—柱状图数据可视化—饼图、环形图、雷达图统…...

LeetCode Hot100 51.N皇后
题目: 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ,返回所有不同的 n 皇后问题 的…...

机器学习 | 贝叶斯方法
不同于KNN最近邻算法的空间思维,线性算法的线性思维,决策树算法的树状思维,神经网络的网状思维,SVM的升维思维。 贝叶斯方法强调的是 先后的因果思维。 监督式模型分为判别式模型和生成式模型。 判别模型和生成模型的区别…...
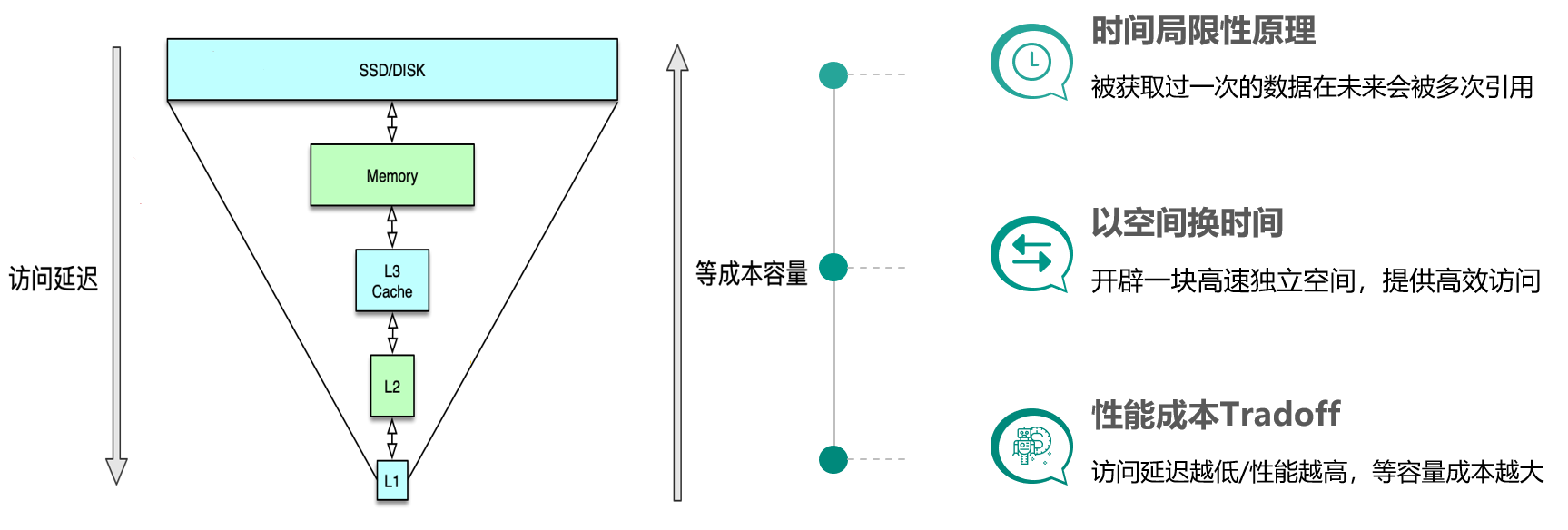
缓存的定义及重要知识点
文章目录 缓存的意义缓存的定义缓存原理缓存的基本思想缓存的优势缓存的代价 缓存的重要知识点 缓存的意义 在互联网高访问量的前提下,缓存的使用,是提升系统性能、改善用户体验的唯一解决之道。 缓存的定义 缓存最初的含义,是指用于加速 …...
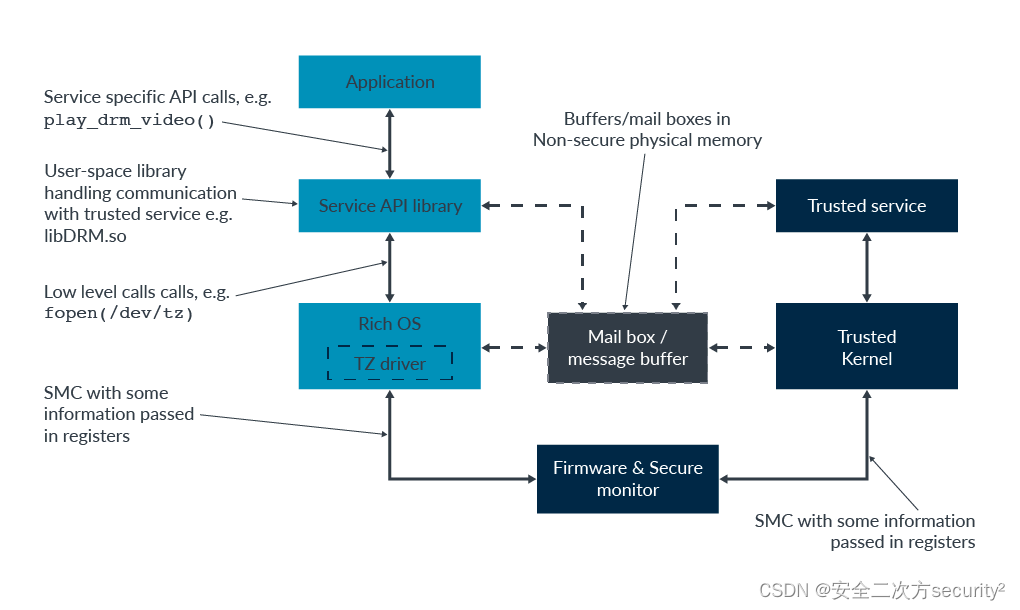
TrustZone之顶层软件架构
在处理器中的TrustZone和系统架构中,我们探讨了硬件中的TrustZone支持,包括Arm处理器和更广泛的内存系统。本主题关注TrustZone系统中发现的软件架构。 一、顶层软件架构 下图显示了启用TrustZone的系统的典型软件栈: 【注意】:为简单起见,该图不包括管理程序,尽管它们可…...
SpringBoot Whitelabel Error Page 报错--【已解决】
springboot 报错信息如下 这个报错页面就是个404 ,代表你访问的url 没有对应的的requestmapping 其实没啥影响的一个问题,但是看到Error 就是不爽,改了他丫的 解决方法如下 一、调整application.properties配置【治标不治本】 server.err…...
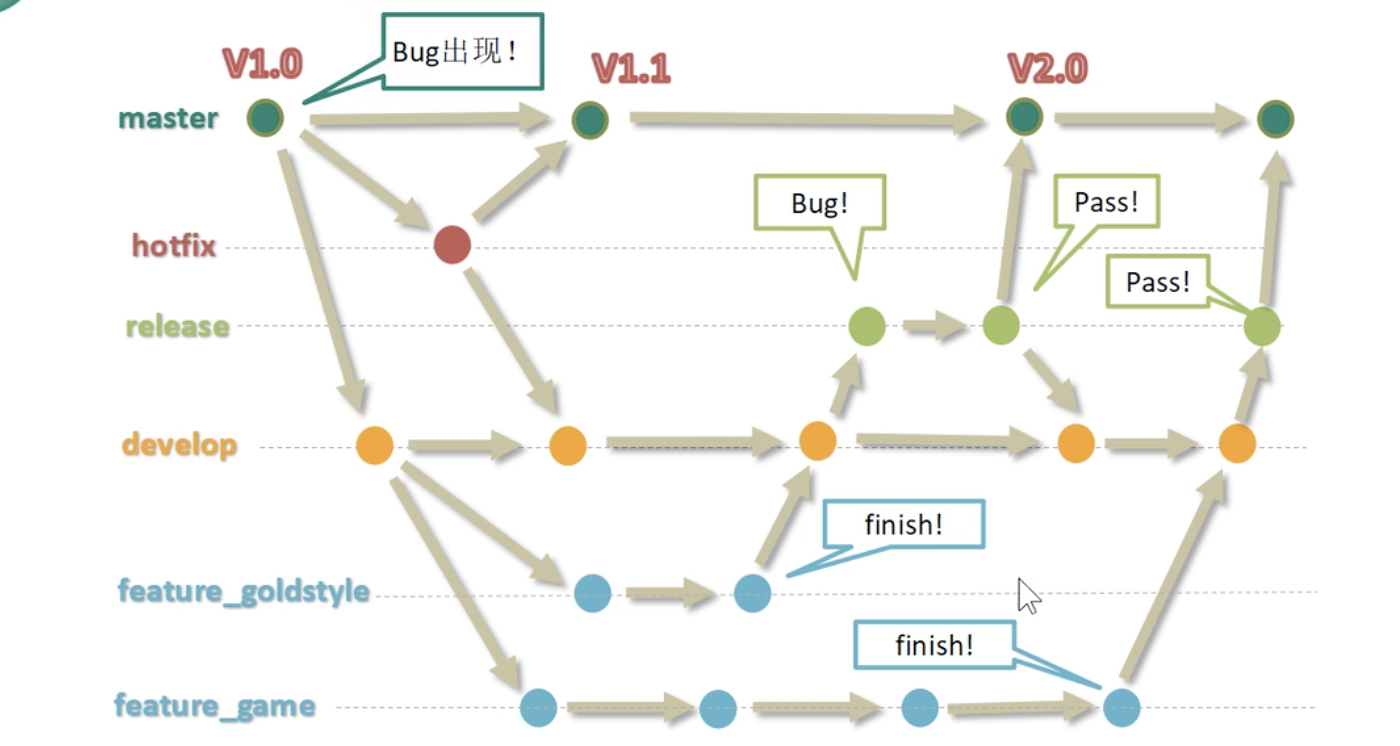
02.Git常用基本操作
一、基本配置 (1)打开Git Bash (2)配置姓名和邮箱 git config --global user.name "Your Name" git config --global user.email "Your email" 因为Git是分布式版本控制工具,所以每个用户都需要…...

黑盒测试中关键截图如何打点
黑盒测试中关键截图如何打点Android黑盒测试过程中如何进行有效的打点是我们经常遇到的问题,我们一般会在脚本内部进行数据打点,也可以使用其他进程录屏或截图。那我们如何选取合适的方式进行打点记录呢?下图是对常用打点方式的统计ÿ…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
