C语言插入排序算法及代码
一、原理
在待排序的数组里,从数组的第二个数字开始,通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
二、代码部分
#include<stdio.h>
#include<stdlib.h>
int main()
{
int arr[10] = { 9,2,1,3,5,4,10,8,6,7 };
int flag = 0, i = 0,j = 0;
printf("排列前:");
for (int i = 0; i < 10; i++)
{
printf("%d ", arr[i]);
}
printf("\n\n");
for (i = 1; i < 10; i++)
{
flag = arr[i]; //记录arr[i] 的值
for (j = i - 1; j >= 0 && arr[j] > flag;j--) //当arr[i]前面的一个数字比a[i]大时
{
arr[j + 1] = arr[j]; //将arr[i] 和其前一个数字进行交换
}
arr[j + 1] = flag;
}
printf("排列后:");
for (int i = 0; i < 10; i++)
{
printf("%d ", arr[i]);
}
printf("\n\n");
system("pause");
return 0;
}
代码输出结果:

三、代码解析
1、核心代码
for (i = 1; i < 10; i++)
{
flag = arr[i]; //记录arr[i] 的值
for (j = i - 1; j >= 0 && arr[j] > flag;j--) //当arr[i]前面的一个数字比arr[i]大时
{
arr[j + 1] = arr[j]; //将arr[i] 和其前一个数字进行交换
}
arr[j + 1] = flag;}
①因为插入排序的执行轮次为 N-1次,所以这里 i 的循环只有 9 次。
② j 循环的作用,通俗来讲就是每次将大于 a[i] 的数字往后各移一个位置。
2、 代码的部分运行过程(带图解)
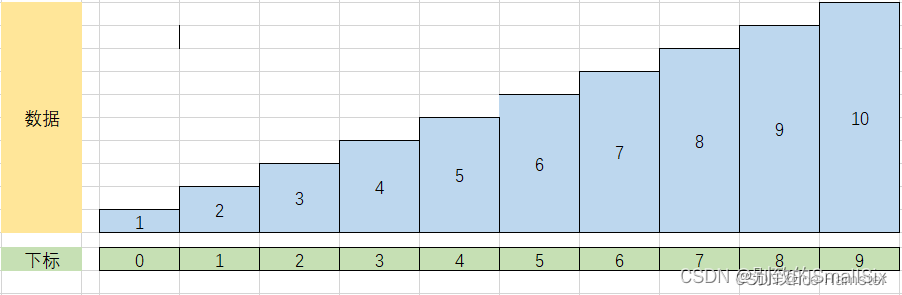
首先见如下原数组各元素的分布情况:
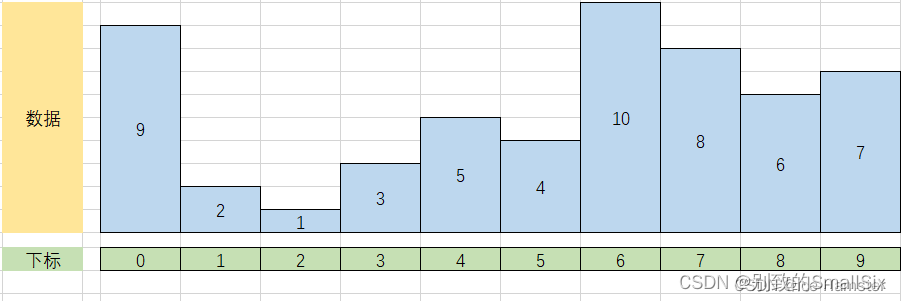
①i = 1,j = 0,flag = 2,进入 j 的循环后,要执行一次,使 arr[1] = 9,然后再执行 arr[j + 1] = flag,让 arr[0] = 2,最后的结果如下:
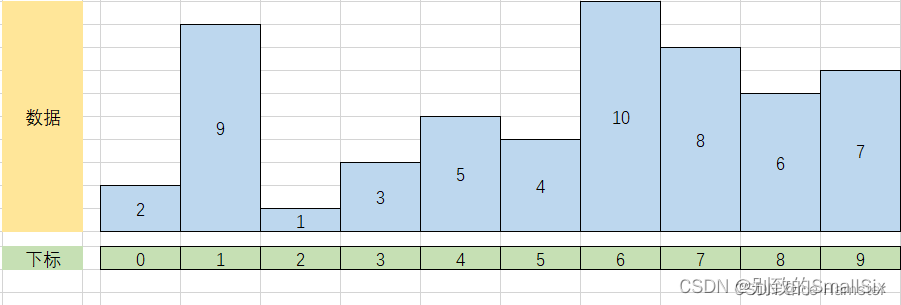
②i = 2,j = 1,flag = 1,进入 j 的循环后,要执行两次,第一次使 arr[2] = 9,第二次使 arr[1] = 2,然后再执行 arr[j + 1] = flag,让 arr[0] = 1,最后的结果如下:
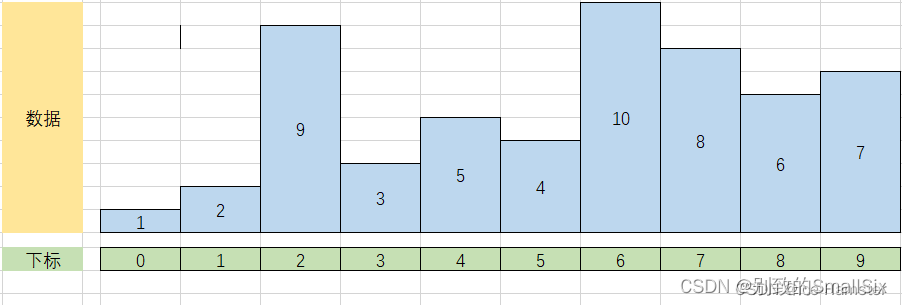
③i = 3,j = 2,flag = 3,进入 j 的循环后,要执行一次,使 arr[3] = 9,然后再执行 arr[j + 1] = flag,让 arr[2] = 3,最后的结果如下:
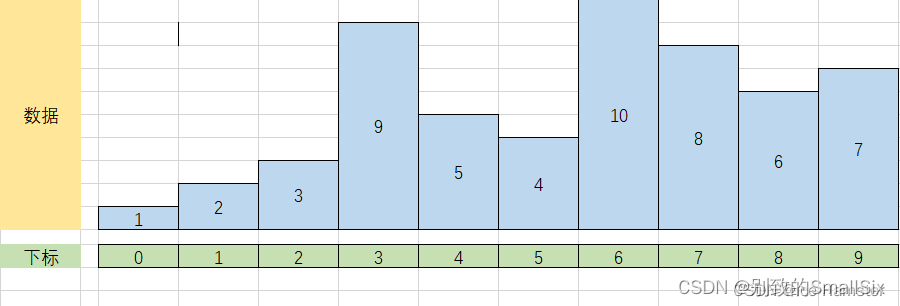
④i = 4,j = 3,flag = 5,进入 j 的循环后,要执行一次,使 arr[4] = 9,然后再执行 arr[j + 1] = flag,让 arr[3] = 5,最后的结果如下:
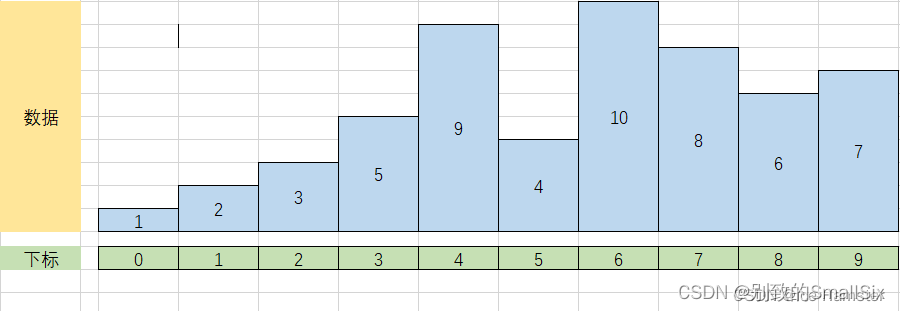
⑤i = 5,j = 4,flag = 4,进入 j 的循环后,要执行两次,第一次使 arr[5] = 9,第二次使arr[4] = 5,然后再执行 arr[j + 1] = flag,让 arr[3] = 4,最后的结果如下:
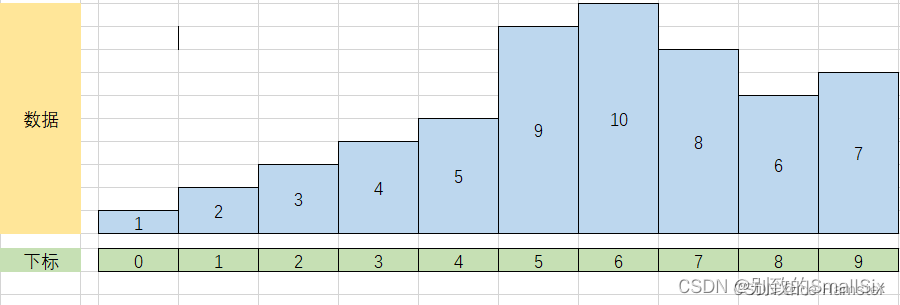
⑥i = 6,j = 5,flag = 10,因为不满足 j 的条件,所以直接执行 arr[j + 1] = flag,让 arr[6] = 10(arr[6] 原本就等于10,这步并未对原数组造成影响)。
⑦i = 7,j = 6,flag = 8,进入 j 的循环后,要执行两次,第一次使 arr[7] = 10,第二次使arr[6] = 9,然后再执行 arr[j + 1] = flag,让 arr[5] = 8,最后的结果如下:
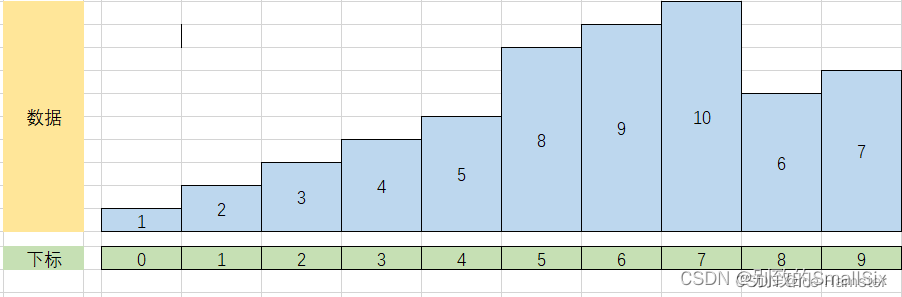
⑧i = 8,j = 7,flag = 6,进入 j 的循环后,要执行三次,第一次使 arr[8] = 10,第二次使arr[7] = 9,第三次使arr[6] = 8,然后再执行 arr[j + 1] = flag,让 arr[5] = 6,最后的结果如下:
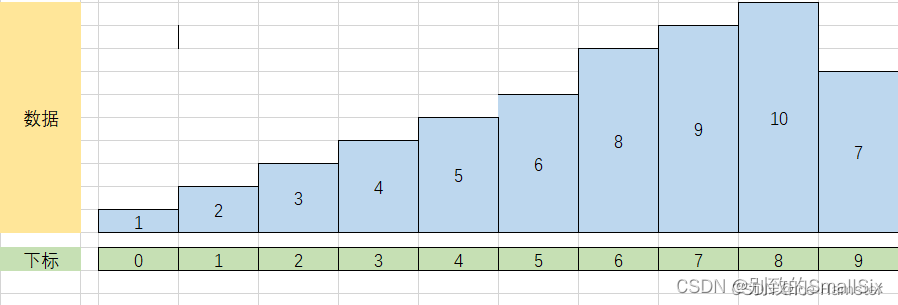
⑨最后一次,i = 9,j = 8,flag = 7,进入 j 的循环后,要执行三次,第一次使 arr[9] = 10,第二次使arr[8] = 9,第三次使arr[7] = 8,然后再执行 arr[j + 1] = flag,让 arr[6] = 7,最后的结果如下(排列完成):
四、总结
插入排序的优点:如果是进行相对有序的数组,效率会非常高。不占额外空间,是一种稳定的算法,编写过程也相对简单,时间复杂度高。
插入排序的缺点:遇到数据过多的情况下不是很适用。
相关文章:

C语言插入排序算法及代码
一、原理 在待排序的数组里,从数组的第二个数字开始,通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。 二、代码部分 #include<stdio.h> #include<stdlib.h> int ma…...
2023年中国法拍房用户画像和数据分析
法拍房主要平台 法拍房主要平台有3家,分别是阿里、京东和北交互联平台。目前官方认定纳入网络司法拍卖的平台共有7家,其中阿里资产司法拍卖平台的挂拍量最大。 阿里法拍房 阿里法拍房数据显示2017年,全国法拍房9000套;2018年&a…...

Android 清除临时文件,清空缓存
python 代码: import os import shutil import tracebackdef delete_folder(path):if os.path.exists(path):print(f"删除文件夹: {path}")shutil.rmtree(path)print("删除完成")def delete_file(path):if os.path.exists(path):print(f"删…...
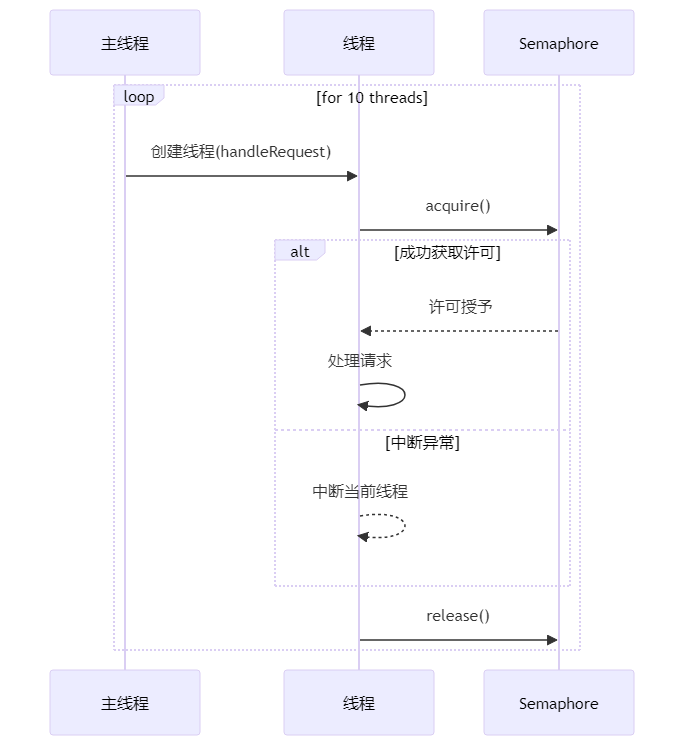
Guava限流神器:RateLimiter使用指南
1. 引言 可能有些小伙伴听到“限流”这个词就觉得头大,感觉像是一个既复杂又枯燥的话题。别急,小黑今天就要用轻松易懂的方式,带咱们一探RateLimiter的究竟。 想象一下,当你去超市排队结账时,如果收银台开得越多&…...

【六大排序详解】开篇 :插入排序 与 希尔排序
插入排序 与 希尔排序 六大排序之二 插入排序 与 希尔排序1 排序1.1排序的概念 2 插入排序2.1 插入排序原理2.2 排序步骤2.3 代码实现 3 希尔排序3.1 希尔排序原理3.2 排序步骤3.3 代码实现 4 时间复杂度分析 Thanks♪(・ω・)ノ下一篇文章见&am…...

凸优化问题求解
这里写目录标题 1. 线性规划基本定理2.单纯形法2.1 转轴运算 3. 内点法3.1 线性规划的内点法 1. 线性规划基本定理 首先我们指出,线性规划均可等价地化成如下标准形式 { min c T x , s . t A x b , x ⪰ 0 , \begin{align}\begin{cases}\min~c^Tx,\\\mathrm{s.…...
文件操作入门指南
目录 一、为什么使用文件 二、什么是文件 2.1 程序文件 2.2 数据文件 2.3 文件名 三、文件的打开和关闭 3.1 文件指针 3.2 文件的打开和关闭 四、文件的顺序读写 编辑 🌻深入理解 “流”: 🍂文件的顺序读写函数介绍: …...

Axure之交互与情节与一些实例
目录 一.交互与情节简介 二.ERP登录页到主页的跳转 三.ERP的菜单跳转到各个页面的跳转 四.省市联动 五.手机下拉加载 今天就到这里了,希望帮到你哦!!! 一.交互与情节简介 "交互"通常指的是人与人、人与计算机或物体…...
)
【数据库设计和SQL基础语法】--连接与联接--多表查询与子查询基础(二)
一、子查询基础 1.1 子查询概述 子查询是指在一个查询语句内部嵌套另一个查询语句的过程。子查询可以嵌套在 SELECT、FROM、WHERE 或 HAVING 子句中,用于从数据库中检索数据或执行其他操作。子查询通常返回一个结果集,该结果集可以被包含它的主查询使用…...
Android studio中导入opencv库
具体opencv库的导入流程参考链接:Android Studio开发之路 (五)导入OpenCV以及报错解决 一、出现的错误:NullPointerException: Cannot invoke “java.io.File.toPath()” because “this.mySdkLocation” is null 解决办法&#…...
_基础知识)
Linux(1)_基础知识
第一部分 一、Linux系统概述 创始人:芬兰大学大一的学生写的Linux内核,李纳斯托瓦兹。 Linux时unix的类系统; 特点:多用户 多线程的操作系统; 开源操作系统; 开源项目:操作系统,应用…...

网络相关面试题
简述 TCP 连接的过程(淘系) 参考答案: TCP 协议通过三次握手建立可靠的点对点连接,具体过程是: 首先服务器进入监听状态,然后即可处理连接 第一次握手:建立连接时,客户端发送 syn 包…...

Vue2面试题:说一下对跨域的理解?
http请求分为两大类:普通http请求(如百度请求)和ajax请求(跨域是出现在ajax请求) 同源策略:在浏览器发起ajax请求时,当前的网址和被请求的网址协议、域名、端口号必须完全一致,目的是…...

Axure中如何使用交互样式交互事件交互动作情形
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《产品经理如何画泳道图&流程图》 ⛺️ 越努力 ,越幸运 目录 一、Axure中交互样式 1、什么是交互样式? 2、交互样式的作用? 3、Axure中如何…...
)
1112. 迷宫(DFS之连通性模型)
1112. 迷宫 - AcWing题库 一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 n∗n 的格点组成,每个格点只有2种状态,.和#,前者表示可以通行后者表示不能通行。 同时当Extense处在某个格点时,他只…...
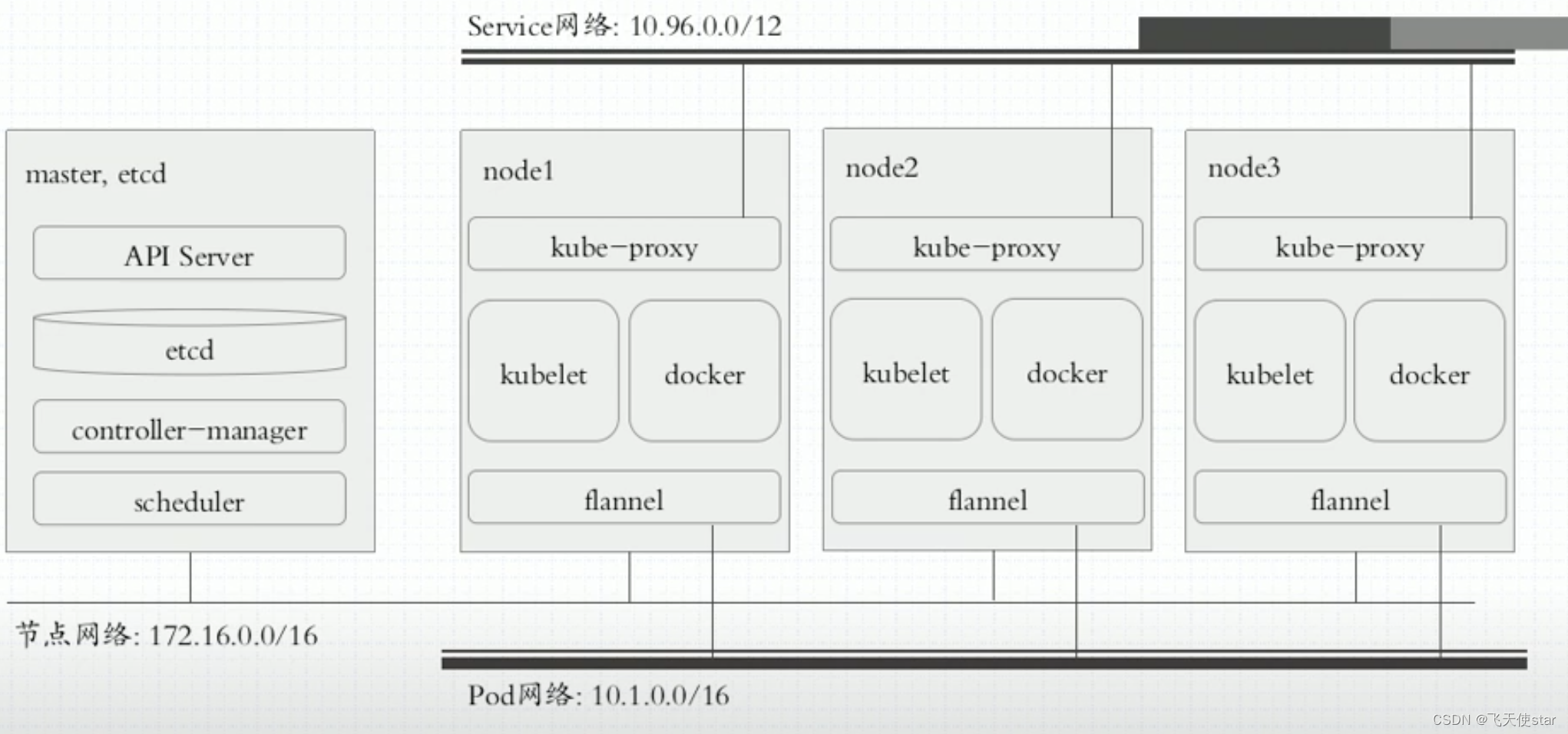
飞天使-k8s知识点1-kubernetes架构简述
文章目录 名词功能要点 k8s核心要素CNCF 云原生框架简介k8s组建介绍 名词 CI 持续集成, 自动化构建和测试:通过使用自动化构建工具和自动化测试套件,持续集成可以帮助开发人员自动构建和测试他们的代码。这样可以快速检测到潜在的问题,并及早…...
linux中deadline调度原理与代码注释
简介 deadline调度是比rt调度更高优先级的调度,它没有依赖于优先级的概念,而是给了每个实时任务一定的调度时间,这样的好处是:使多个实时任务场景的时间分配更合理,不让一些实时任务因为优先级低而饿死。deadline调度…...

jquery、vue、uni-app、小程序的页面传参方式
jQuery、Vue、Uni-app 和小程序(例如微信小程序)都有它们自己的页面传参方式。下面分别介绍这几种方式的页面传参方式: jQuery: 在jQuery中,页面传参通常是通过URL的查询参数来实现的。例如: <a href"page2…...
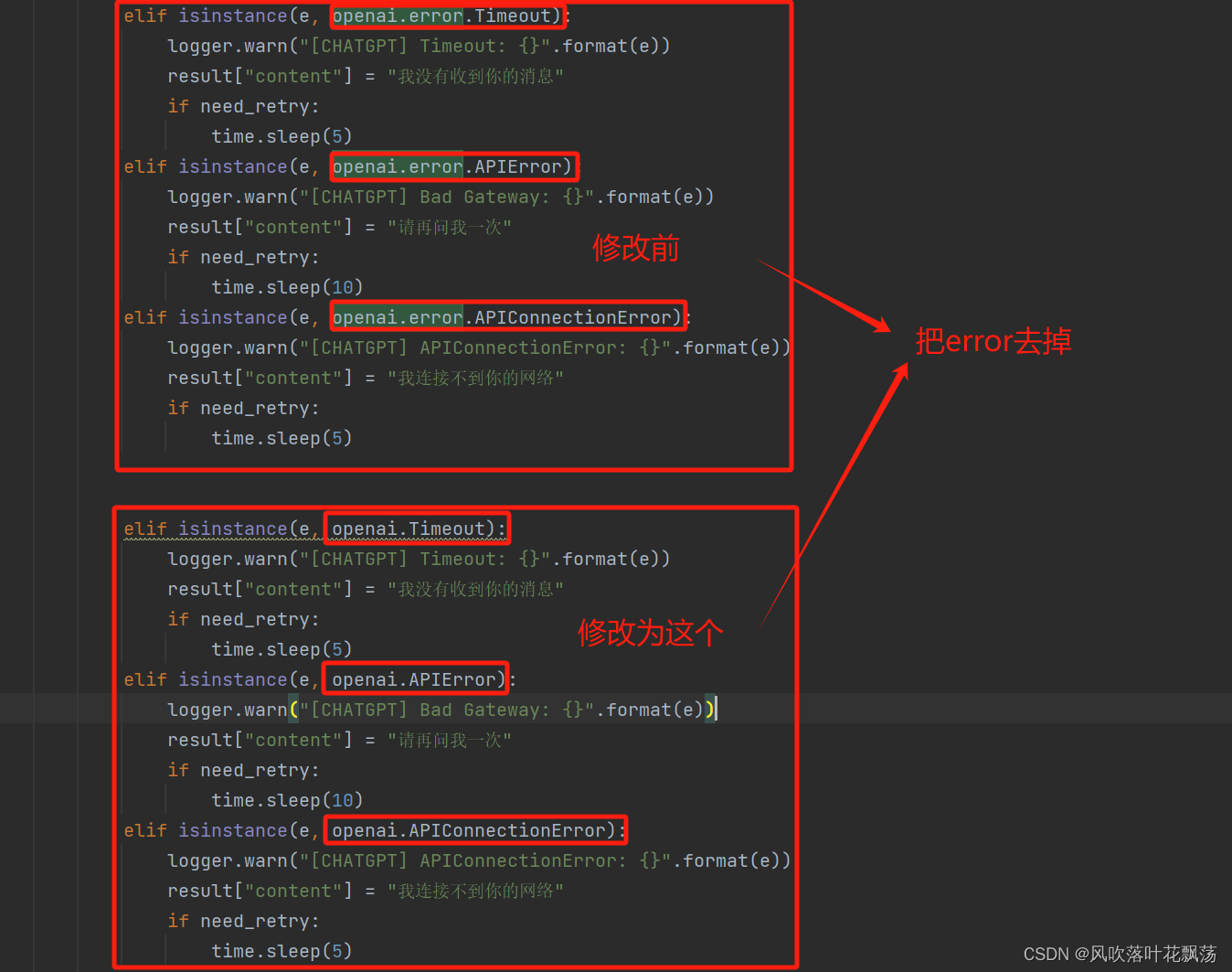
ModuleNotFoundError: No module named ‘openai.error‘
ModuleNotFoundError: No module named ‘openai.error’ result self.fn(*self.args, **self.kwargs) File “H:\chatGPTWeb\chatgpt-on-wechat\channel\chat_channel.py”, line 168, in _handle reply self._generate_reply(context) File “H:\chatGPTWeb\chatgpt-on-wec…...

理解pom.xml中的parent标签
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: 循序渐进学SpringBoot ✨特色专栏&…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
