管理类联考——数学——真题篇——按题型分类——充分性判断题——蒙猜E
老老规矩,看目录,平均每年2E,跟2D一样,D是全对,E是全错,侧面也看出10道题,大概是3A/B,3C,2D,2E,其实还是蛮平均的。但E为1道的情况居多。
第20题如果要硬猜,要不就是留给E吧

再把其他年份的第20题找出来,选了A或D,也就是说,第20题,验证了A的有效性,无效,就直接选E,有效,就还得验证B,B有效,就选D。

最后,第20题是分水岭,前面除了第17题,其他不大可能选E。即第20题之前若判断A,B都不充分,那么就选C。或者就把所有感觉要联立都选C,从C中找E,哈哈,不过这个概率说不定更低。
文章目录
- 2023
- 真题(2023-20)-E-不要被选项迷惑,不是取值范围,是两个不同未知数;-选项特点:一个大于号,一个小于号,两个未知数;
- 真题(2023-21)-E-选项特点:两个已知X的值;
- 2022
- 真题(2022-20)-E;选项特点-一个已知,一个只有;
- 真题(2022-23)-E-容易误判C,因为【一个等号+一个不等号】
- 2021
- 真题(2021-17)-E-要不要联立-要联立选C;(我爱说实话)两个条件看起来确实很像需要联立的样子
- 真题(2021-23)-E-易误判选C,因为【一个不等号,一个等号】
- 2020
- 真题(2020-20)-E
- 真题(2020-22)-E-条件轮换对称+结论要求具体某个量(不对称)-条件未知量轮换对称:轮换对称:a→b→c→d轮换位置后条件表达式不变;很容易误选C,因为【一个等号+一个不等号】
- 2019
- 真题(2019-22)-E选项蒙猜-特别难的结论就直接过;(我爱说实话,这个第一眼也像可以联合)
- 2018
- 真题(2018-21)-E;(我爱说实话,这个第一眼也像可以联合)
- 2017
- 真题(2017-20)-E;选项特点:两个已知X的值(这个特点没啥用,因为ABCD都出现)
- 2016
- 真题(2016-20)-E-看起来好像联合可以出答案的样子
- 2015
- 真题(2015-20)-E-看起来好像联合可以出答案的样子;-选项特点:和等式,积等式。
- 2014
- 2013
- 真题(2013-17)-E-特别难的结论选E(我爱说实话,考试想不到这个点);选E选项往往不需要联合,联合的选C的几率高
选E选项(条件1和条件2单独都不充分,联合起来也不充分)
对学员的掌握程度要求更高
判断误差的罪魁祸首,是E,在不确定的情况下,宁愿把E选成别的选项,也不要把别的选项选成E。
1.往往不需要复杂的推理或计算。通过特殊反例,常识,逻辑关系可看出来。
2.选E选项往往不需要联合,联合的选C的几率高。
真题:2013年17题;2012年21题;
自从13年出现“可确定”型题目,E选项绝大部分出自此类题目
1.特别难的结论就直接过;
真题:19年22题,13年01,17题
2.不满足“要啥给啥”原则:
(1)条件(比例关系)与所求结论(具体量)信息类型不匹配;
(2)条件(范围)与所求结论(具体量)信息类型不匹配;
真题:13年10月20题(缺少相关年份真题)
3.条件轮换对称+结论要求具体某个量(不对称)
条件未知量轮换对称;轮换对称:a→b→c→d轮换位置后条件表达式不变;
真题:20年22题。
2023
真题(2023-20)-E-不要被选项迷惑,不是取值范围,是两个不同未知数;-选项特点:一个大于号,一个小于号,两个未知数;
-几何-解析几何;
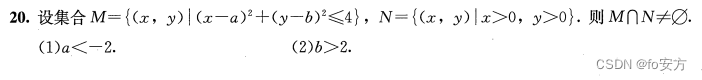

真题(2023-21)-E-选项特点:两个已知X的值;
-应用题-路程


2022
真题(2022-20)-E;选项特点-一个已知,一个只有;
-简单算术题
20.将 75 名学生分成 25 组,每组 3 人,则能确定女生人数。
(1)已知全是男生的组数和全是女生的组数。
(2)只有1男的组和只有1女的组数相等。

真题(2022-23)-E-容易误判C,因为【一个等号+一个不等号】
-数列-等比数列-等比中项;+一元二次函数
23.已知𝑎,𝑏为实数,则能确定𝑎的值。
(1)𝑎,𝑏,𝑎 + 𝑏成等比数列。
(2)𝑎(𝑎 + 𝑏) > 0。

2021
真题(2021-17)-E-要不要联立-要联立选C;(我爱说实话)两个条件看起来确实很像需要联立的样子
-应用题-工程
17.清理一块场地,则甲乙丙三人能在2天内完成。
(1)甲乙两人需要3天完成。
(2)甲丙两人需要4天完成。

真题(2021-23)-E-易误判选C,因为【一个不等号,一个等号】
-应用题-路程
23.某人开车去上班,有一段路因维修限速通行,则可以算出此人上班的距离。
(1)路上比平时多用了半小时。
(2)已知维修路段的通行速度。

2020
真题(2020-20)-E
-代数-方程-出现了两个及以上未知量,而数量关系却少于未知量的个数-整数不定方程-先根据题目转化为ax+by=c形式的不定方程,然后结合整除、倍数和奇偶特征分析讨论求解
20、共有n 辆车,则能确定人数。
(1)若每辆车 20 座,1 车未满。
(2)若每辆车 12 座,则少 10 个座。


真题(2020-22)-E-条件轮换对称+结论要求具体某个量(不对称)-条件未知量轮换对称:轮换对称:a→b→c→d轮换位置后条件表达式不变;很容易误选C,因为【一个等号+一个不等号】
-E-代数-方程-出现了两个及以上未知量,而数量关系却少于未知量的个数-整数不定方程-先根据题目转化为ax+by=c形式的不定方程,然后结合整除、倍数和奇偶特征分析讨论求解
22、已知甲、乙、丙三人共捐款 3500 元,则能确定每人的捐款金额。
(1)三人的捐款金额各不相同。
(2)三人的捐款金额都是 500 的倍数。



2019
真题(2019-22)-E选项蒙猜-特别难的结论就直接过;(我爱说实话,这个第一眼也像可以联合)
-E-算术-整除
22、设 n 为正整数,则能确定n 除以 5 的余数。
(1) 已知 n 除以 2 的余数。
(2) 已知n 除以 3 的余数。


2018
真题(2018-21)-E;(我爱说实话,这个第一眼也像可以联合)
-应用题-简单算术
21.甲购买了若干件 A 玩具,乙购买了若干件 B 玩具送给幼儿园,甲比乙少花了 100 元,则能确定甲购买的玩具件数。
(1)甲与乙共购买了 50 件玩具。
(2)A 玩具的价格是 B 玩具的 2 倍。

E。本题考查方程组相关知识。假设甲的玩具价格为每件x元,共买了A件,乙的玩具价格为每件y元,共买了B件,题干前提条件为Ax+100=By,其中,x,y,A,B均为未知数。条件(1)为A+B=50 ,条件(2)为x=2y,显然,无论条件(1)、(2)单独,还是联合,未知数个数都多于方程个数,无唯一解,不能确定未知数A的值,都不充分。


2017
真题(2017-20)-E;选项特点:两个已知X的值(这个特点没啥用,因为ABCD都出现)
-比例应用题-增长率
20.能确定某企业产值的月平均增长率。
(1)已知一月份的产值。
(2)已知全年的总产值答案。


答案应该是E。(否则2017年没有选E)
首先理解“月平均增长率x”:只与第一个月和最后一个月的产值有关。如:一月a、二、三、四…十一、十二月3a: a ( 1 + x ) 11 = 3 a a(1+x)^{11}=3a a(1+x)11=3a,得 ( 1 + x ) 11 = 3 (1+x)^{11}=3 (1+x)11=3,得: x = 3 11 − 1 x=\sqrt[11]{3}-1 x=113−1
∴(2)全年总产值是无关的。更改为“12月的产值”,才选C。
2016
真题(2016-20)-E-看起来好像联合可以出答案的样子
-应用题-溶液
20.将 2 升甲酒精和 1 升乙酒精混合,得到丙酒精,则能确定甲、乙两种酒精的浓度。
(1)1 升甲酒精和 5 升乙酒精混合后的浓度是丙酒精浓度的 1 2 \frac{1}{2} 21倍。
(2)1 升甲酒精和 2 升乙酒精混合后的中毒是丙酒精浓度的 2 3 \frac{2}{3} 32倍。

2015
真题(2015-20)-E-看起来好像联合可以出答案的样子;-选项特点:和等式,积等式。
-数列-等差数列
20.设{ a n a_n an}是等差数列,则能确定数列{ a n a_n an}
(1) a 1 + a 6 = 0 a_1+a_6=0 a1+a6=0
(2) a 1 a 6 = − 1 a_1a_6=-1 a1a6=−1

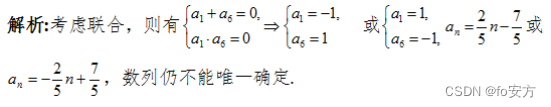
2014
我14年没有E,没人来管管的吗
2013
真题(2013-17)-E-特别难的结论选E(我爱说实话,考试想不到这个点);选E选项往往不需要联合,联合的选C的几率高
-E-算术-质合数
17. p = m q + 1 p = mq + 1 p=mq+1为质数。
(1) m m m为正整数, q q q为质数。
(2) m , q m,q m,q均为质数。


相关文章:

管理类联考——数学——真题篇——按题型分类——充分性判断题——蒙猜E
老老规矩,看目录,平均每年2E,跟2D一样,D是全对,E是全错,侧面也看出10道题,大概是3A/B,3C,2D,2E,其实还是蛮平均的。但E为1道的情况居多。 第20题…...
】)
【Linux基本指令(2)】
文章目录 一. 基本指令第二回 一. 基本指令第二回 cp指令语法 cp src dst 将目标文件或者目录拷贝到指定目录下或文件下。注意同级目录下,不允许存在同名文件或同名目录。如果将一个file.txt文件拷贝到当前目录下,就重名了,报错cp不了&#…...

Debian系统设置SSH密钥登陆
如果没有安装ssh,root权限运行apt install openssh-server进行安装。 ssh-keygen -t rsa # 生成配对密钥,后续一路enter即可会在用户目录(即~这个)下生成.ssh文件夹,里面的id_rsa是私钥,id_rsa.pub是公钥…...

uniapp cli开发和HBuilderX开发
uniapp cli开发和HBuilderX开发 前言 uniapp是一个跨平台的开发框架,可以开发出微信小程序、支付宝小程序、百度小程序、头条小程序、H5、App等,开发者只需要写一套代码,就可以发布到各个平台,大大提高了开发效率。 uniapp的开…...
【Java异常】idea 报错:无效的目标发行版:17 的解决办法
【Java异常】idea 报错:无效的目标发行版:17 的解决办法 一,问题来源 springcloud的第一个demo项目就给我干趴了 二、原因分析 java: 无效的目标发行版: 17 原因就是 JDK 版本不对。从 IDEA 编辑器中可以找到问题的原因所在,…...

代码提交规范-ESLint+Prettier+husky+Commitlint
代码提交规范-ESLintPrettierhuskyCommitlint 配置eslint (3步)配置prettier(4步)1.安装配置prettier2.设置忽略文件 .prettierignore3.处理eslint冲突4. 配置vscode 的settings.json husky安装并配置lint-staged(3步)安装配置com…...
)
手动实现 Vue 3的简易双向数据绑定(模仿源码)
Vue 3 带来了许多令人兴奋的新特性和改进,其中之一就是其双向数据绑定的实现方式。与 Vue 2 使用 Object.defineProperty 不同,Vue 3 利用了 JavaScript 的 Proxy 特性来创建响应式数据。在这篇博客中,我们将探讨 Vue 3 中双向数据绑定的基础…...
LVS最终奥义之DR直接路由模式
1 LVS-DR(直接路由模式) 1.1 LVS-DR模式工作过程 1.客户端通过VIP将访问请求报文(源IP为客户端IP,目标IP为VIP)发送到调度器 2.调度器通过调度算法选择最适合的节点服务器并重新封装数据报文(将源mac地址改为调度器的mac地址&am…...
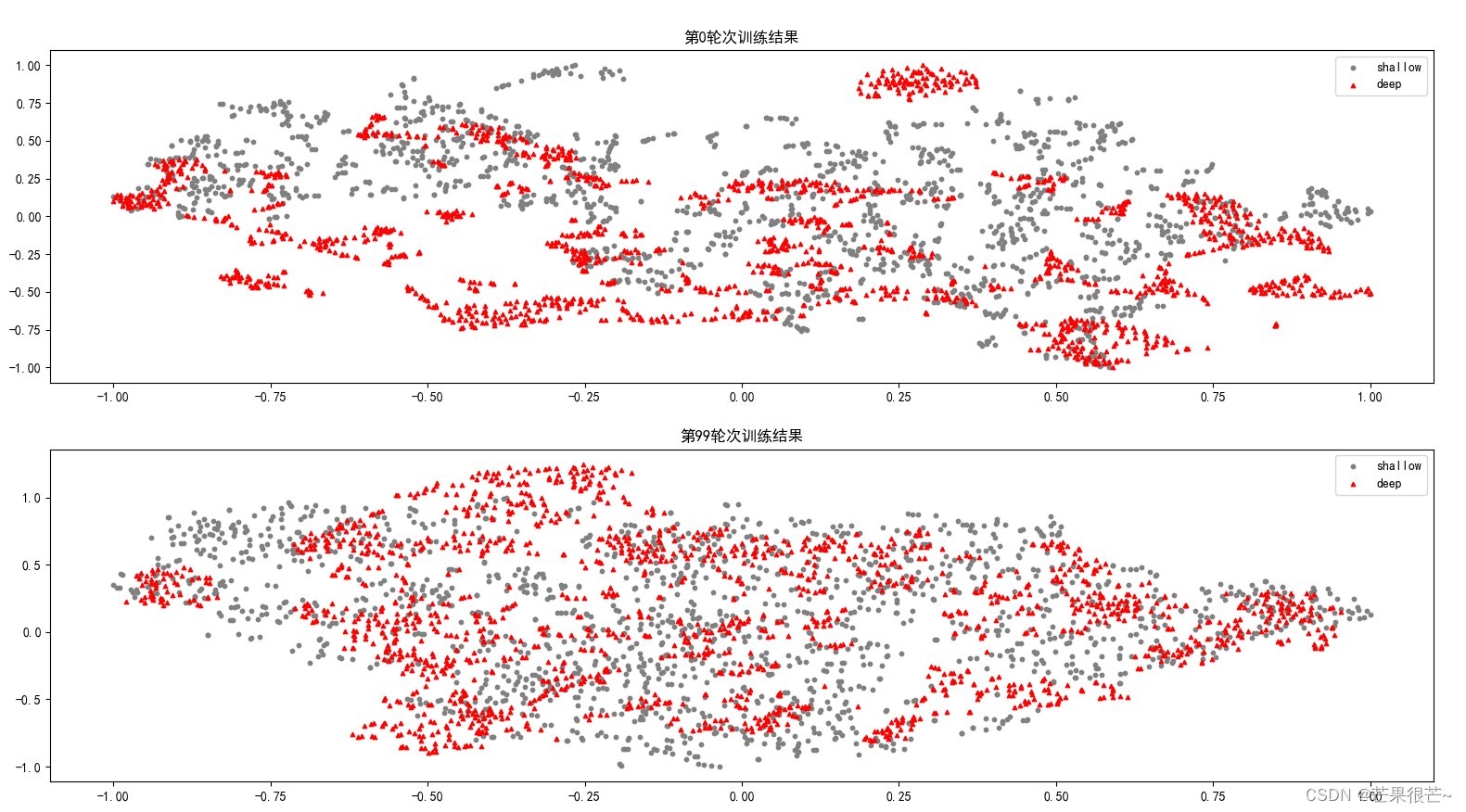
t-SNE高维数据可视化实例
t-SNE:高维数据分布可视化 实例1:自动生成一个S形状的三维曲线 实例1结果: 实例1完整代码: import matplotlib.pyplot as plt from sklearn import manifold, datasets """对S型曲线数据的降维和可视化"&q…...

配置应用到k8s
配置应用到k8s,前置条件是安装了Docker,Minikube,kubectl 应用已经通过Docker生成本地镜像文件 1,创建godemo-deployment.yaml apiVersion: apps/v1kind: Deploymentmetadata:name: godemo-deploymentspec:replicas: 3 #启动三个…...

(四)STM32 操作 GPIO 点亮 LED灯 / GPIO工作模式
目录 1. STM32 工程模板中的工程目录介绍 2. GPIO 简介 3. GPIO 框图剖析 1)保护二极管及上、下拉电阻 2) P-MOS 管和 N-MOS 管 3)输出数据寄存器 3.1)ODR 端口输出数据寄存器 3.2)BSRR 端口位设置/清除寄存器 4&a…...
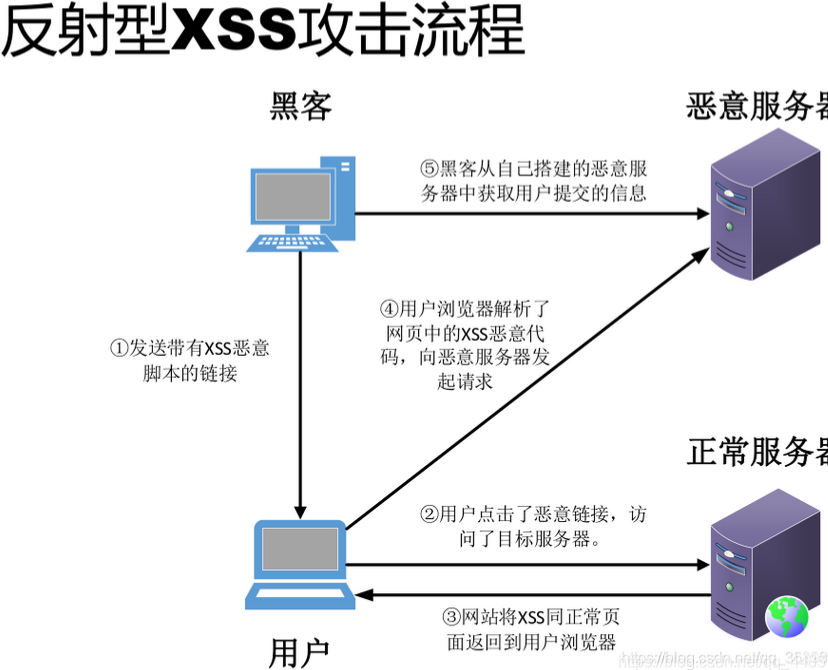
你知道跨站脚本攻击吗?一篇带你了解什么叫做XSS
1.XSS简介 (1)XSS简介 XSS作为OWASP TOP 10之一。 XSS中文叫做跨站脚本攻击(Cross-site scripting),本名应该缩写为CSS,但是由于CSS(Cascading Style Sheets,层叠样式脚本&#x…...
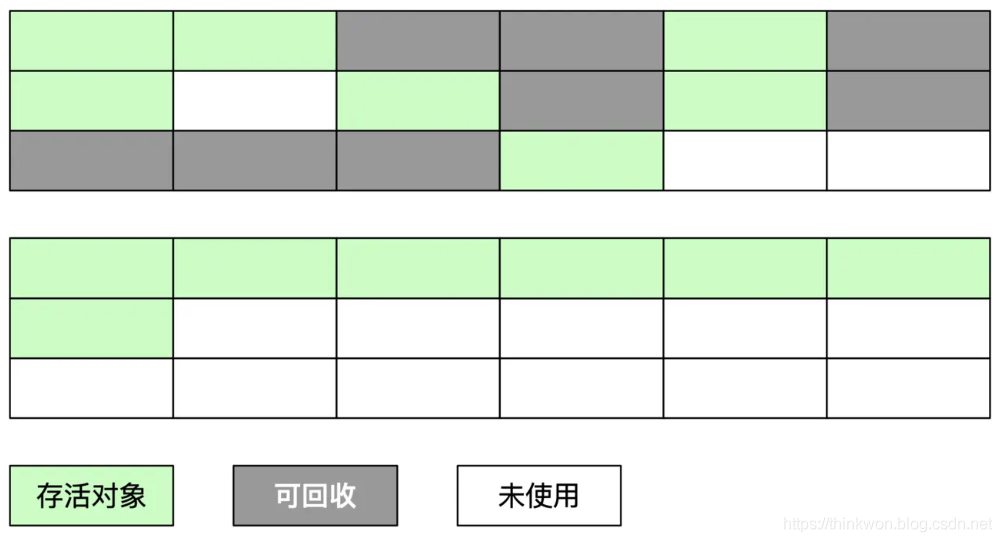
JVM入门
JVM概述 JVM位置 JVM体系结构 注意:栈中一定不存在垃圾,栈中数据用完一个弹出一个,总结来说,栈区、本地方法栈、程序计数器这三块必定不存在垃圾。JVM调优主要是针对方法区、堆(99%)进行调优。 常用的第三…...
)
Cmake基础(5)
这篇文章主要描述如何使用cmake构建一个库工程 文章目录 add_libraryinstall 库工程的代码:头文件和源文件 #ifndef ADD_H #define ADD_H#ifdef _WIN32 #ifdef MYMATH_EXPORTS #define MYMATH_API __declspec(dllexport) #else #define MYMATH_API __declspec(dll…...

Rabbitmq 死信取消超时订单
本文使用的版本 otp_win64_25.0rabbitmq-server-3.11.26rabbitmq插件 rabbitmq_delayed_message_exchange-3.11.1 pom.xml文件 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId> …...

C语言—每日选择题—Day55
指针相关博客 打响指针的第一枪:指针家族-CSDN博客 深入理解:指针变量的解引用 与 加法运算-CSDN博客 第一题 1. 若有如下定义,则 p1&m;p2p1; 是正确赋值语句.说法是否正确? int *p1; int *p2; int m …...

软件测试岗位的简历怎么写?项目怎么包装
已经帮大家打包好了包装好的简历模板,大家可以直接进行套用,详情请望下看 自动化测试相关教程推荐: 2023最新自动化测试自学教程新手小白26天入门最详细教程,目前已有300多人通过学习这套教程入职大厂!!_哔哩哔哩_bili…...

服务器解析漏洞是什么?攻击检测及修复
服务器解析漏洞(Server-side Include Vulnerability,SSI漏洞)是一种安全漏洞,通常出现在支持服务器端包含(SSI)功能的Web服务器上。SSI是一种在Web页面中嵌入动态内容的技术,允许开发人员将外部…...

HTML---CSS美化网页元素
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 一.div 标签: <div>是HTML中的一个常用标签,用于定义HTML文档中的一个区块(或一个容器)。它可以包含其他HTML元素,如文本、图像…...

【Docker】基础篇
文章目录 Docker为什么出现容器和虚拟机关于虚拟机关于Docker二者区别: Docker的基本组成相关概念-镜像,容器,仓库安装Docker卸载docker阿里云镜像加速docker run的原理**为什么容器比虚拟机快**Docker的常用命令1.帮助命令2.镜像相关命令3.容…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
