【学习笔记】NOMURA Programming Competition 2020
C - Folia
不难想到自底向上确定树的形态。可能要多尝试一下
一开始想错了好几个地方,服了
假设某一层有XXX个节点,那么上一层可能有⌈X2⌉,⌈X2⌉+1,...,X\lceil\frac{X}{2}\rceil,\lceil\frac{X}{2}\rceil+1,...,X⌈2X⌉,⌈2X⌉+1,...,X个节点(不包括叶子节点),那么我们可以很容易的递推求出每一层的[li,ri][l_i,r_i][li,ri]表示这一层点数的取值范围。但是并不是每一层的rir_iri都是能取到的,因为ri≤2ir_i\le 2^iri≤2i,而且2i2^i2i比较大不太好处理。
基于上述两个理由,我们考虑自顶向下确定每一层点的取值,每一层贪心取最大点数即可。并且可以证明答案不会超过long long
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define fi first
#define se second
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
int n,a[100005];
ll l[100005],r[100005],res=1;
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n;for(int i=0;i<=n;i++)cin>>a[i];if(n&&a[0]){cout<<-1;return 0;}l[n]=r[n]=a[n];for(int i=n-1;i>=0;i--){l[i]=a[i]+(l[i+1]+1)/2;r[i]=a[i]+r[i+1];}if(l[0]>1){cout<<-1;return 0;} ll X=1;for(int i=1;i<=n;i++){X=min(r[i],2*(X-a[i-1]));if(X<l[i]){cout<<-1;return 0;}res+=X;}cout<<res;
}
D - Urban Planning
对于给定的{pi}\{p_i\}{pi},贡献就是nnn减去连通块的个数。
笑死,然而还是不会做
注意到{pi}\{p_i\}{pi}对应导出的图是一个基环树森林,因此环的数目等于连通块的数目,要算所有情况下环数目的和,可以对于每个环单独考虑它出现次数的方案数。该死,为什么我这一步都没转化出来就像计数了啊
然后先考虑pi=−1p_i=-1pi=−1的情形。不过这道题的突破口好像不在这里,因为随便用组合数算算没啥难度
还是要考虑题目给定的{pi}\{p_i\}{pi}长什么样子。奇怪啊,竟然要对这一点特别提出来考虑 我们发现,其给出的图一定是由若干内向基环树和内向树构成 刚开始把内向树想成链了,真是奇怪。假设有MMM个基环树,那么对答案造成的贡献是固定的M(N−1)KM(N-1)^KM(N−1)K;假设有K′K'K′个内向树,那么只有根节点指向的边不是固定的,注意我们的目标还是数环。
为什么题解的式子这么简洁
定义环上的关键点为内向树的根节点以及pi=−1p_i=-1pi=−1的那些点。记这些点为{ai}\{a_i\}{ai},子树大小为{bi}\{b_i\}{bi},那么方案数为(n−1)!(N−1)K−n∏bi(n-1)!(N-1)^{K-n}\prod b_{i}(n−1)!(N−1)K−n∏bi,其中nnn表示环上的点数。不难证明这个计数方式不重不漏。
复杂度O(n2)O(n^2)O(n2)。代码非常简单,只需要一个简单的背包即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mod=1e9+7;
int n,m,K,fa[5005],p[5005],sz[5005],vs[5005];
ll fac[5005],F[5005],dp[5005],res;
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);
}
int main(){cin>>n;for(int i=1;i<=n;i++)fa[i]=i,sz[i]=1;fac[0]=F[0]=1;for(int i=1;i<=n;i++)fac[i]=fac[i-1]*i%mod,F[i]=F[i-1]*(n-1)%mod;for(int i=1;i<=n;i++){cin>>p[i];K+=(p[i]==-1);if(~p[i]){int u=find(i),v=find(p[i]);if(u!=v){fa[u]=v,sz[v]+=sz[u];}else{vs[u]=1,m++;}}}dp[0]=1;for(int i=1;i<=n;i++){if(fa[i]==i){if(!vs[i]){res=(res+(sz[i]-1)*F[K-1])%mod;for(int j=n;j>=1;j--){dp[j]=(dp[j]+dp[j-1]*sz[i])%mod;}}else{res=(res+F[K])%mod;}}}for(int i=2;i<=K;i++){if(dp[i]){res=(res+fac[i-1]*dp[i]%mod*F[K-i])%mod;}}cout<<(F[K]*n-res+mod)%mod;
}
E - Binary Programming
姑且先把这套题做着吧,其他的题也没精力翻了
考虑倒着做,然后贪心 这个过程中可能会产生一堆假做法,但是不要慌张 。
我企图直接贪心,然而产生了错误,我是joker,这里数据删除了
从何贪起呢,我们观察到111一定是放在最后删的,事实上这也是一个非常显然的结论。另一个观察我没有注意到,那就是无论怎么操作,相邻两个111对答案的贡献都是一样的,因此我们考虑把相邻的111删去,这样就不存在相邻的111了 。
然后就非常好搞了。设某个111前面000的个数为xxx,后面000的个数为yyy,那么对于奇数位上的111,贡献最大是⌊x2⌋+1+y\lfloor\frac{x}{2}\rfloor+1+y⌊2x⌋+1+y,对于偶数位上的111,贡献最大是⌊x−12⌋+1+y\lfloor\frac{x-1}{2}\rfloor+1+y⌊2x−1⌋+1+y,显然这是可以取到的。
复杂度O(n)O(n)O(n)。
做这种题比较爽的地方是只要有了正确的思路就很好搞,不然就会有很多种情况
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n;
ll res,zero,one,sum;
char s[200005];
int main(){scanf("%s",s+1),n=strlen(s+1);for(int i=1;i<=n;i++)sum+=(s[i]=='0');for(int i=1;i<=n;i++){if(s[i]=='0'){zero++;}else{one++;if(i+1<=n&&s[i+1]=='1'){res+=sum+1;one++;i++;}else{if(one&1)res+=zero/2+1+sum-zero;else res+=(zero-1)/2+1+sum-zero;}}}for(int i=1;i<=one;i++){res+=i/2;}cout<<res;
}
F - Sorting Game
该死,看到后面把前面的操作忘了,直接把Snuke\text{Snuke}Snuke的操作搞忘了,怪不得做不出来,先数据删除一波
一看到这个邻值交换就感到非常亲切,序列{ai}\{a_i\}{ai}合法等价于对于任意i<ji<ji<j,从高往低位找到第一个ci=1,cj=0c_i=1,c_j=0ci=1,cj=0时,其后面数位上的数完全相同。
嗯,读错题过后少考虑了一些因素,反而有帮助?
但是这个限制显然不能拿来直接计数。因为是平时训练题所以也懒得打表
到这里能发散的点还是挺多的,直接猜结论可能不一定会导向正确的方向
这题好做的原因可能还是在于没有什么特殊的限制,因此大胆猜测最终dpdpdp式子并不复杂
观察这个限制有点像数位dpdpdp。那么最基础的想法就是从高到低位考虑,打个表观察一下,于是不难发现这个想法的动机 然而这不是我最初的思路。。。 :对于i<ji<ji<j,aia_iai和aja_jaj的最高位分别是111,000,那么其剩余的数位一定完全相同。首先我们要知道,对于不存在子串101010的情况,其方案数等价于dpn,m−1dp_{n,m-1}dpn,m−1。其中dpn,mdp_{n,m}dpn,m表示nnn个数,mmm个数位的方案数。
另一方面,如果存在这样的i,ji,ji,j,我们猜测可以把i,ji,ji,j以及它之间的东西一起压缩掉变成同一个数,假设中间有KKK个位置最高位不确定那么剩下的方案数就是dpn−K−1,m−1dp_{n-K-1,m-1}dpn−K−1,m−1 。中间KKK个数最高位可以任取,方案数2K2^K2K。于是留给了我们一个艰巨的任务:证明这样的方案数是等价的。
至于这么压缩为什么是等价的,可以先写代码验证一番 ,或者更严谨地,因为后面数位的数都是复制粘贴所以可以只保留i,ji,ji,j两个数,因为不存在101010所以都只能比后j−1j-1j−1位,于是就是等价的。
综上所述,dpn,m=(n+1)×dpn,m−1+∑k=0n−2dpn−k−1,m−1×2k×(n−k−1)dp_{n,m}=(n+1)\times dp_{n,m-1}+\sum_{k=0}^{n-2}dp_{n-k-1,m-1}\times 2^k\times (n-k-1)dpn,m=(n+1)×dpn,m−1+∑k=0n−2dpn−k−1,m−1×2k×(n−k−1)。
利用换元把式子写成dpn,m=(n+1)×dpn,m−1+∑k=1n−1dpk,m−1×2n−1−k×kdp_{n,m}=(n+1)\times dp_{n,m-1}+\sum_{k=1}^{n-1}dp_{k,m-1}\times 2^{n-1-k}\times kdpn,m=(n+1)×dpn,m−1+∑k=1n−1dpk,m−1×2n−1−k×k 就可以O(1)O(1)O(1)转移了。
复杂度O(nm)O(nm)O(nm)。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mod=1e9+7;
int n,m;
ll dp[5005][5005],sum[5005][5005],F[5005],F2[5005];
int main(){cin>>m>>n;F[0]=1;for(int i=1;i<=n;i++)F[i]=F[i-1]*2%mod;F2[0]=1;for(int i=1;i<=n;i++)F2[i]=F2[i-1]*(mod+1)/2%mod;for(int j=1;j<=m;j++){dp[0][j]=1;for(int i=1;i<=n;i++){if(j>1){dp[i][j]=((i+1)*dp[i][j-1]+sum[i-1][j-1]*F[i-1])%mod;}else{dp[i][j]=F[i];}sum[i][j]=(sum[i-1][j]+dp[i][j]*F2[i]%mod*i)%mod;}}cout<<dp[n][m];
}
相关文章:

【学习笔记】NOMURA Programming Competition 2020
C - Folia 不难想到自底向上确定树的形态。可能要多尝试一下 一开始想错了好几个地方,服了 假设某一层有XXX个节点,那么上一层可能有⌈X2⌉,⌈X2⌉1,...,X\lceil\frac{X}{2}\rceil,\lceil\frac{X}{2}\rceil1,...,X⌈2X⌉,⌈2X⌉1,...,X个节点&…...
)
iis下常用程序的伪静态规则列表(包括wordpress、thinkphp)
shopex discuz2.0 discuz2.5 discuz3.x 淘宝客 ecshop phpwind参照http://www.west.cn/faq/list.asp?unid797通过主机面板设置即可 wordpress设置: 第一步: 1.新建一个“chineseurl.php”文件:在里面写入以下代码上传到wordpress安装目录。…...

【Python语言基础】——Python Select From
Python语言基础——Python Select From 文章目录 Python语言基础——Python Select From一、Python Select From一、Python Select From 从表中选取 如需从 MySQL 中的表中进行选择,请使用 “SELECT” 语句: 实例 从表 “customers” 中选取所有记录,并显示结果: import m…...
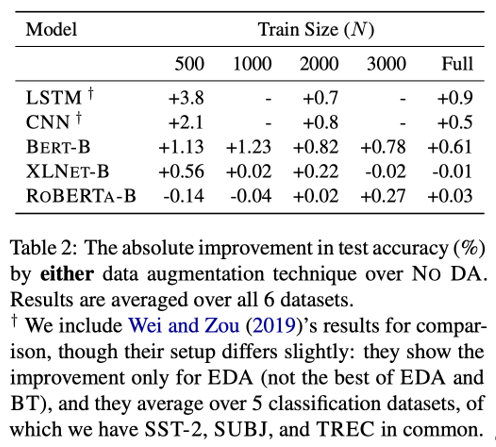
数据增广真有那么神奇吗?
作者:皮皮雷 来源:投稿 编辑:学姐 论文题目 How Effective is Task-Agnostic Data Augmentation for Pretrained Transformers? 论文作者 S. Longpre, Y. Wang, and C. DuBois 论文发表于 2020 EMNLP findings 摘要 任务无关的数据增广…...

常用基础硬件知识 - 判断MOS管导通
目录1. 概述2. 判断MOS管的导通1. 概述 本文主要记录下基础的硬件知识,方便自己查阅。 2. 判断MOS管的导通 在产品硬件设计中,有时需要程序控制一些电源使能。 1.原理图已经标出了G极(gate)—栅极、S极(source)—源极、D极(drain)—漏极。 如果没有标…...
2023金三银四,测试人还能找到好工作吗?
嫌看文章麻烦的朋友点这里:2023最新软件测试行业变革细谈之我们该如何应对? 按照往年的惯例,春节后复工的 3 月、4 月是人员跳槽最频繁的时候,俗称“金三银四”。然而,市场大环境的影响,很多行业感受到了一…...

c++构造函数
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录一、构造函数1.构造函数的形式2.构造函数的调用时机3.委托构造函数4.复制构造函数二、析构函数本文仅为个人笔记 视频链接:https://www.bilibili.com/vid…...
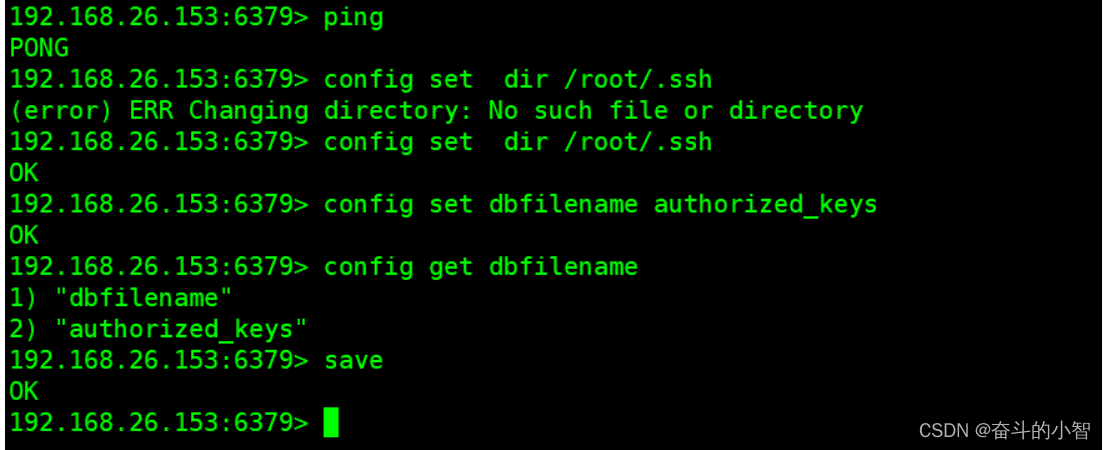
redis 未授权访问漏洞
redis 未授权访问漏洞 目录 redis 未授权访问漏洞 漏洞描述 漏洞原因: 漏洞危害 漏洞复现: 漏洞复现 写webshell: 写计划任务:centos默认在/var/spool/cron 写ssh公钥实现ssh登录: 漏洞描述: Redis默认情况下…...

如何制作一个自定义的winpe?
winpe制作过程 获取相关资源 https://www.aliyundrive.com/s/MP58JbRsm76 文件存放位置 将压缩包存放在一个全英文目录下了,我这里选择了D:/winpe目录 解压文件 将三个压缩包进行解压到当前目录,如下图所示 创建一个mount目录,并在mount目录下分别创建boot和install目…...

QString转为2进制,8进制,10进制,16进制介绍
首先看段代码: bool ok false;QString ss "11";qDebug()<<"-----"<<ss.toInt(&ok,2)<<ss.toInt(&ok,10)<<ss.toInt(&ok,16)<<ss.toInt(&ok,8);结果: ----- 3 11 17 9 bool ok fal…...

2023-3-2-22:01随笔
好久没怎么更新技术分享博客了。去年从2022年1月3日到2023年1月份一直专注于ADAS的行车横向功能的研发与实车调试,2022年写了几篇项目经验的文章,像LQR算法(虽然和同事(志同道合,技术追求的民哥)写出的工程…...
学习红客技术必备,手把手教你成为“安防第一人”
互联网时代已悄悄来临,作为新时代的人们,我们日常生活、工作、学习方面都需要借助互联网来完成,这样,又产生一种新的问题,那就是网络安全的问题,有时我们拼命加班好不容易完成的东西,在一夜之间…...
Git系列:常见指令辨析
Git系列:常见指令辨析指令辨析工作区、暂存区、版本库傻傻分不清楚?主干和分支的关系是什么?git fetch/merge/pull辨析日志查看时,git log与git reflog的区别是?git diff和status的区别是?相关资料本文小结…...

并发编程实战-构建自定义的同步工具
文章目录1.状态依赖性的管理1.1 示例:将前提条件的失败传递给调用者1.2 示例:通过轮询与休眠来实现简单的阻塞1.3 条件队列2.使用条件队列2.1 条件谓词2.2 过早唤醒2.3 丢失的信号2.4 通知2.5 示例:阀门类2.6 子类的安全问题2.7 入口协议与出…...
HBase集群部署
目录 一、前期准备 二、HBase下载 1. 查看HBase与hadoop版本对应关系 2. hbase的下载 3. 将hbase的tar包上传到linux 下 二、安装hbase 1. 解压 2. HBase的文件配置 主机名hadoop版本HBase版本hadoop安装路径Hbase安装路径HadoopMaster3.3.02.4.3/home/hadoop/softwareh…...
网络传输:linux下的网络请求和下载(ping wget curl)、端口
一、下载和网络请求 1.ping命令 可以通过ping命令,检查指定的网络服务器是否可连通状态 语法:ping [-c num] ip或主机名 选项: -c 检查的次数,若不使用-c,将无限次数持续检查参数:ip或主机名,…...

阅读(1)-----六级
目录 1.单词不懂怎么办? 1.1构词法 1.2上下文 2.句子不通怎么办? 3.时间不够怎么办 ? 4.题型 4.1细节题 问文章的细节 4.2主旨题(文章主旨和段落主旨) 4.3语义题 4.4观点题 (一共三种,支持、反对和中立 &…...

【Python实战】快看:”又中奖了,中大奖了“周围的小伙伴都惊呆了~你还不麻溜滴~(代码版彩票小游戏上线啦)
导语 哈喽!北鼻们,晚上好。 夕阳🌇的第一缕阳光送给小可爱们~每天都要加油鸭! 所有文章完整的素材源码都在👇👇 粉丝白嫖源码福利,请移步至CSDN社区或文末公众hao即可免费。 彩票是一个恒古不…...

【python】控制台中文输出乱码解决方案
注:最后有面试挑战,看看自己掌握了吗 文章目录控制台原因解决方法方法一方法二方法三如果是os.system函数乱码控制台原因 一般的情况下,还是我们的源码文件的编码格式问题。我们一般是要把源码文件的编码格式改成utf-8就好了,但是…...

一名IC验证工程师的成长路径是怎么样的?来听听工程师的见解
IC验证这个岗位对于非科班的学生是比较友好的,因为验证需要具备的技能UVM,SV,C等,非科班和科班的差距不会拉开太大。因其岗位需求量巨大而格外受到了大家的青睐,甚至成为不少学生的转行首选。 验证对于IC的重要性 IC…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
