线性表,也是Java中数组的知识点!
线性表定义:
由n (n≥0)个数据特性相同的元素构成的有限序列称为线性表,(n=0)的时候被称为空表。
线性表的顺序表示
线性表的顺序存储又被称为顺序表
-
优点
- 无需为表示表中元素之间的逻辑关系而增加额外的存储空间
- 可以随意读取任意位置的元素
-
缺点
-
插入或者删除,需要移动大量数据元素
-
线性表长度变化较大时,难以确定存储空间的容量
-
造成存储空间的碎片
-
java中用数组表示的:
double[] a = new double[N];
声明初始化数组:
int[] a = { 1, 1, 2, 3, 5, 8 };
数组一经创建,它的大小就是固定的。程序能够通过 a.length 获取数组 a[] 的长度,而它的最后一个元素总是 a[a.length – 1]。
典型的数组处理代码:
找出数组中最大的元素
double max = a[0];
for (int i = 1; i < a.length; i++)if (a[i] > max) max = a[i];
计算数组元素的平均值
int N = a.length;
double sum = 0.0;
for (int i = 0; i < N; i++)sum += a[i];
double average = sum / N;
复制数组
int N = a.length;
double[] b = new double[N];
for (int i = 0; i < N; i++)b[i] = a[i];
颠倒数组元素的顺序
int N = a.length;
for (int i = 0; i < N/2; i++)
{double temp = a[i];a[i] = a[N-1-i];a[N-i-1] = temp;
}
矩阵相乘(方阵) a[] [ ] * b[] [] = c[] []
int N = a.length;
double[][] c = new double[N][N];
for (int i = 0; i < N; i++)for (int j = 0; j < N; j++){ // 计算行 i 和列 j 的点乘for (int k = 0; k < N; k++)c[i][j] += a[i][k]*b[k][j];}
二维数组
在 Java 中二维数组就是一维数组的数组。大多数情况下(根据合适的参数 M 和 N)我们都会使用 M×N,即 M 行长度为 N 的数 组的二维数组(也可以称数组含有 N 列)。
二维数组 a[][] 的 第 i 行第 j 列的元素可以写作 a [i] [j]
创建时:double[] [] a = new double [M] [N]
其根本是等价于:
double[][] a;
a = new double[M][N];
for (int i = 0; i < M; i++)for (int j = 0; j < N; j++)a[i][j] = 0.0;Java 会将数值类型的数组元素初始化为 0,将布尔型的数组元素初始化为 false。但是如果想要初始化为其他值,我们就需要嵌套的 for 循环设置自己想要的值。
稀疏数组 (sparsearray)
比如像五子棋棋盘,用二维数组存棋盘上的点。假设0为空,1是黑棋,2是白棋;那么前面会有很多默认值0,这样子记录了很多没价值的数据。这个时候就是稀疏数组的用武之地。
一个数组中大部分元素为0,或者为同一个值的数组时,可以使用稀疏数组来保存该数组。
稀疏数组的处理方法是:
-
记录数组一共有几行几列,有多少个不同的值
-
把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模
具体实施:
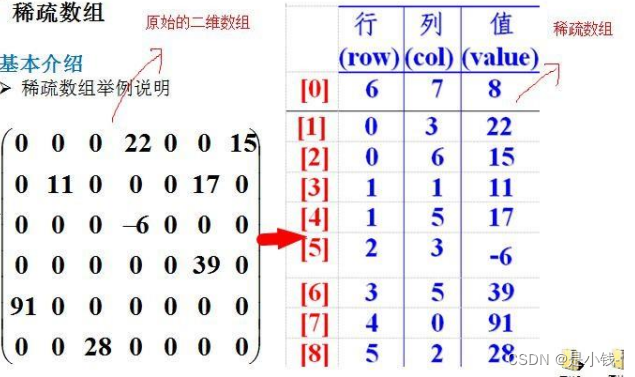
固定是3列。第一行是共有几行几列,有多少个不同的值 ,后面则是将每个特殊的元素所在的行列和值记录下来。
二维数组 转 稀疏数组的思路
1.遍历原始的二维数组,得到有效数据的个数sum
// 前面已经创建了原始二维数组,且用0表示没有棋子,1表示黑棋 2表示白棋int sum = 0;
for (int i = 0; i < 11; i++) {for (int j = 0; j < 11; j++) {if (chessArr1[i][j] != 0) {sum++;}}
}
2.根据sum就可以创建稀疏数组sparseArr int [sum+1] [3]
int sparseArr[][] = new int[sum + 1][3];3.将二维数组的有效数据数据存入到稀疏数组
// 给稀疏数组赋值
sparseArr[0][0] = 11;
sparseArr[0][1] = 11;
sparseArr[0][2] = sum;
// 遍历二维数组,将非 0 的值存放到 sparseArr 中
int count = 0; //count 用于记录是第几个非 0 数据
for (int i = 0; i < 11; i++) {for (int j = 0; j < 11; j++) {if (chessArr1[i][j] != 0) {count++;sparseArr[count][0] = i; //row列记录行sparseArr[count][1] = j; //col列记录列sparseArr[count][2] = chessArr1[i][j]; //value列记录值}}
}
稀疏数组转原始的二维数组的思路
1.先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组,比如上面的 chesArr2=int[11] [11]
int chessArr2[][] = new int[sparseArr[0][0]][sparseArr[0][1]];
2.再读取稀疏数组后几行的数据,并赋给 原始的二维数组 即可
for(int i = 1; i < sparseArr.length; i++) {// 二维数组【行=稀疏数组[i][0]行的值】【列=稀疏数组[i][1]列的值】//= 值(稀疏数组第三列的值)chessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
}相关文章:

线性表,也是Java中数组的知识点!
线性表定义: 由n (n≥0)个数据特性相同的元素构成的有限序列称为线性表,(n0)的时候被称为空表。 线性表的顺序表示 线性表的顺序存储又被称为顺序表 优点 无需为表示表中元素之间的逻辑关系而增加额外的存储空间可以随意读取任意位置的元素 缺点 插入…...

java使用面向对象实现图书管理系统
꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN …...

2023 英特尔On技术创新大会直播 |我感受到的“芯”魅力
文章目录 每日一句正能量前言AI时代,云与PC结合为用户带来更好体验全新处理器,首次引入针对人工智能加速的NPU大模型时代,软硬结合带来更好训练成果后记 每日一句正能量 成长是一条必走的路路上我们伤痛在所难免。 前言 在2023年的英特尔On技…...
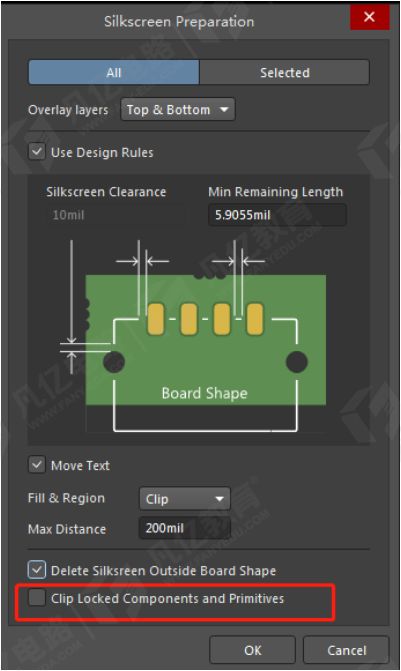
Atium Designer 23 全新功能-丝印制备,解决DFM问题
进行PCB设计时需要养成良好的设计习惯,才能保证后期的生产效果。例如整板上需要保证丝印跟阻焊的间距规则避免产生丝印重叠造成的PCB制造设计(DFM)问题。丝印重叠阻焊的影响有如下: 1)PCB板后期打样,一般是…...
Nginx快速入门:安装目录结构详解及核心配置解读(二)
0. 引言 上节我们讲解了nginx的应用场景和安装,本节继续针对nginx的各个目录文件进行讲解,让大家更加深入的认识nginx。并通过一个实操案例,带大家来实际认知nginx的核心配置 1. nginx安装目录结构 首先nginx的默认安装目录为:…...

测试TensorFlow/PyTorch的GPU版本是否启用
文章目录 1. Pytorch测试代码2. TensorFlow测试代码 后续遇到好的会不断更新。。。 1. Pytorch测试代码 import torch def gpu_is_available():print(\nGPU details:)print(f gpu_is_available : , torch.cuda.is_available())print(f cuda_device_count : , t…...
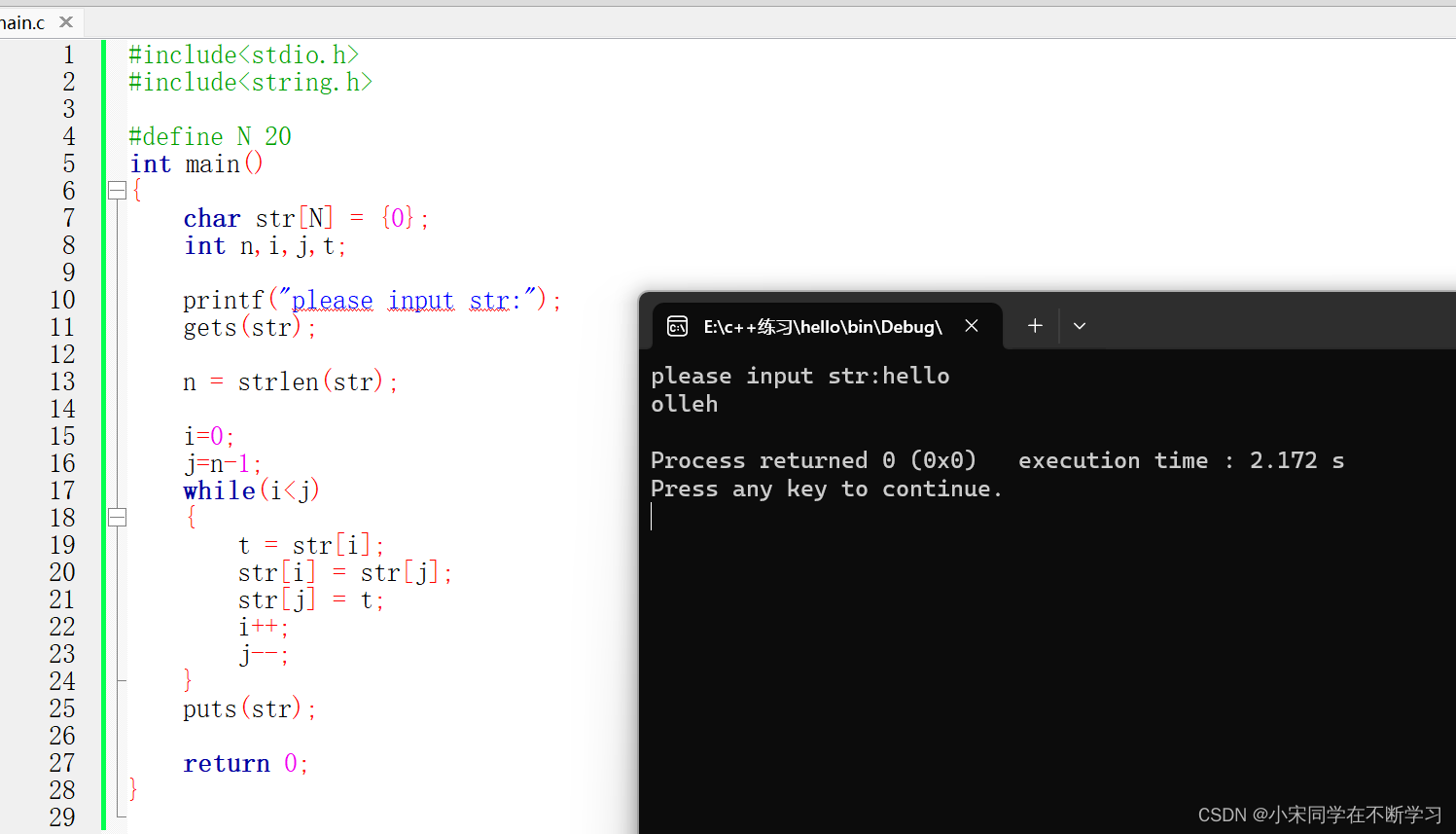
字符串逆序输出
逆序输出就是本来abc输出的,然后我想让他输出成cba,那么我们还是要用到for循环,只不过原先是从零开始往上加,这回呢,是从上面往下减 我们观察上面这个图片,我们想要输出olleh,那么我们就要从4开…...

期货平仓日历(期货平仓日期汇总)
什么是期货平仓日历? 期货是一种高风险高收益的投资品种。而期货交易不同于股票等其他投资品种的交易,期货交易需要在一定时间内才能买卖。而期货平仓日历就是指期货交易中规定的所有合约的平仓日期汇总。 常见期货平仓日期和时间? 不同的…...
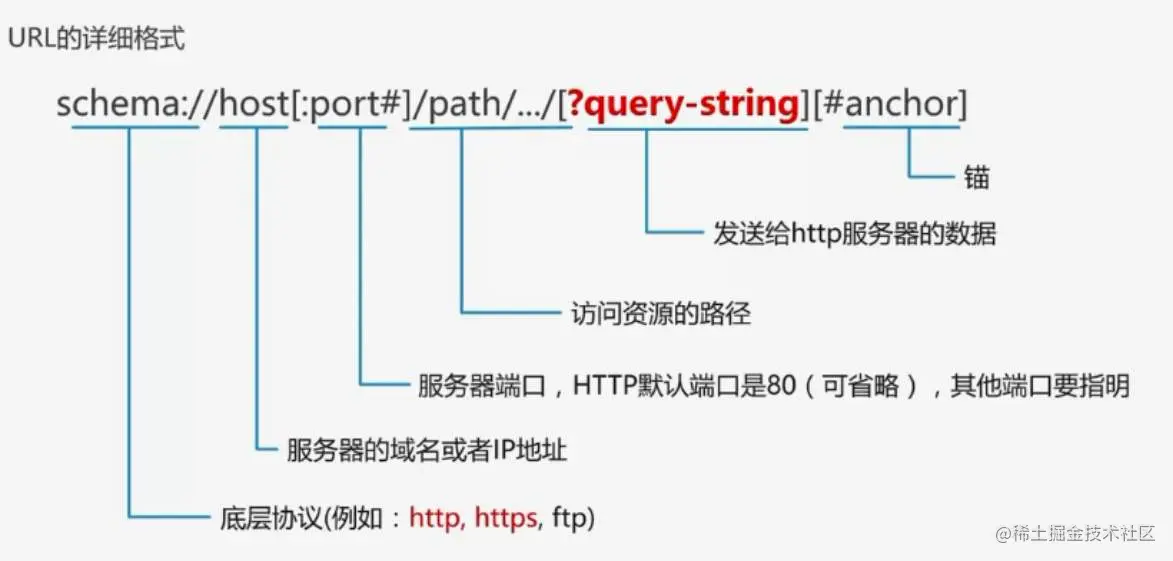
计算机网络-进阶
目录 易混淆物理层数据链路层网络层nat如何实现私有ip通信IP数据报 格式解析tcp 连接tcp流量控制滑动窗口拥塞控制 报文捕获 wireshark路由模拟器 enspcdn代理服务器 VS cdn VS web cache 计算机有了物理地址,为什么还要有ip地址?单播 多播 广播 传输层会…...
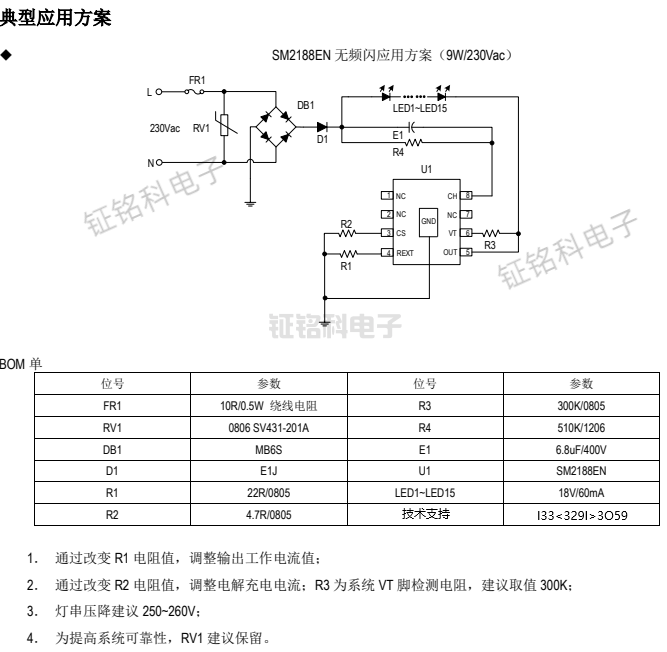
LED恒流驱动芯片SM2188EN:满足LED灯具出口欧盟所需的ERP能效认证标准和要求
LED灯具是一种节能环保的照明产品,因其高效节能、长寿命等优点而备受消费者青睐,成为照明市场的主流产品。作为LED灯具出口欧盟市场的必备条件,ERP能效认证标准和要求对LED灯具的能效性能提出了严格的要求。 首先,ERP能效认证标准…...

RocketMQ系统性学习-RocketMQ原理分析之消费者的接收消息流程
🌈🌈🌈🌈🌈🌈🌈🌈 【11来了】文章导读地址:点击查看文章导读! 🍁🍁🍁🍁🍁🍁dz…...

butterfly蝴蝶分类
一、分类原因 由于植物分类所使用的数据集存在一定问题,修改起来比较麻烦,本次采用kaggle的ButterflyMothsImageClassification数据集,对100这种蝴蝶进行分类。 二、100中蝴蝶类别 ‘ADONIS’,‘AFRICAN GIANT SWALLOWTAIL’,‘AMERICAN S…...

计算机基础:网络基础
目录 一.网线制作 1.制作所需要工具 网线制作标准 编辑 2.水晶头使用 3.网线钳使用 4.视频教学 二.集线器、交换机介绍 1.OSI七层模型 2.TCP/IP四层参考模型 3.集线器、交换机。路由器介绍 集线器 交换机 路由器 区别 三.路由器的配置 1.路由器设置 说明书 设…...

[原创][R语言]股票分析实战[3]:周级别涨幅趋势的相关性
[简介] 常用网名: 猪头三 出生日期: 1981.XX.XX QQ联系: 643439947 个人网站: 80x86汇编小站 https://www.x86asm.org 编程生涯: 2001年~至今[共22年] 职业生涯: 20年 开发语言: C/C、80x86ASM、PHP、Perl、Objective-C、Object Pascal、C#、Python 开发工具: Visual Studio、D…...
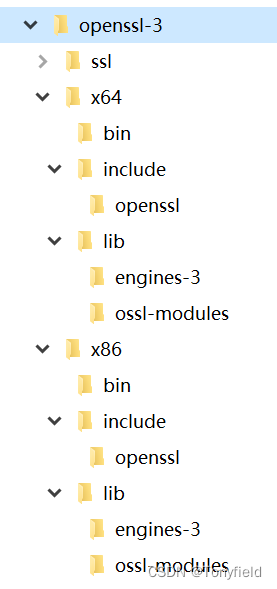
MSVC编译 openssl windows 库
开发需要在windows下集成 openssl 库,参考官方指导完成了编译:openssl/NOTES-WINDOWS.md at master openssl/openssl 不过,最后还是走了直接下载的捷径。 1. 安装 ActivePerl 需要在 ActiveState 注册账户,之后彼会提供具体的…...

electron兼容统信UOS系统过程中的坑
这里写目录标题 找统信支持人员咨询过,他们说不对electron提供支持,如果需要兼容统信UOS还是建议换个开发技术gbm_bo_map--no-sandboxNo protocol specified任务栏图标总结 找统信支持人员咨询过,他们说不对electron提供支持,如果…...

Flink系列之:Apache Kafka SQL 连接器
Flink系列之:Apache Kafka SQL 连接器 一、Apache Kafka SQL 连接器二、依赖三、创建Kafka 表四、可用的元数据五、连接器参数六、特性七、Topic 和 Partition 的探测八、起始消费位点九、有界结束位置十、CDC 变更日志(Changelog) Source十一…...

灰盒测试简要学习指南!
在本文中,我们将了解什么是灰盒测试、以及为什么要使用它,以及它的优缺点。 在软件测试中,灰盒测试是一种有用的技术,可以确保发布的软件是高性能的、安全的并满足预期用户的需求。这是一种从外部测试应用程序同时跟踪其内部操作…...
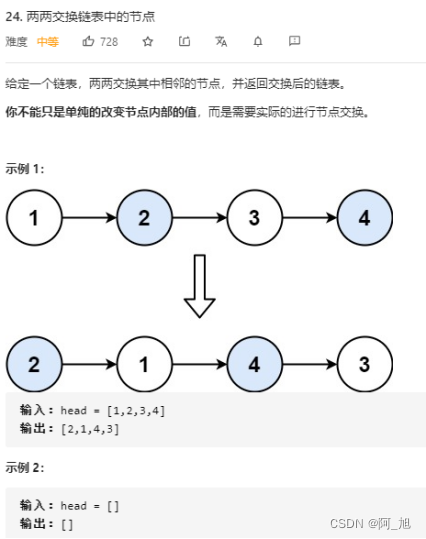
【经典LeetCode算法题目专栏分类】【第7期】快慢指针与链表
《博主简介》 小伙伴们好,我是阿旭。专注于人工智能AI、python、计算机视觉相关分享研究。 ✌更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~ 👍感谢小伙伴们点赞、关注! 快慢指针 移动零 class…...
springboot解决XSS存储型漏洞
springboot解决XSS存储型漏洞 XSS攻击 XSS 攻击:跨站脚本攻击(Cross Site Scripting),为不和 前端层叠样式表(Cascading Style Sheets)CSS 混淆,故将跨站脚本攻击缩写为 XSS。 XSS(跨站脚本攻击):是指恶意攻击者往 Web 页面里插…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
