信息论安全与概率论
目录
一. Markov不等式
二. 选择引理
三. Chebyshev不等式
四. Chernov上限
4.1 变量大于
4.2 变量小于
信息论安全中会用到很多概率论相关的上界,本文章将梳理几个论文中常用的定理,重点关注如何理解这些定理以及怎么用。
一. Markov不等式
假定X为非负且为实数的随机变量,令为该变量的数学期望,可得:
理解:代表事件的集合,该定理用来描述概率的上界,且该上界与数学期望相关。
二. 选择引理
令,左边的
代表随机变量,右边
代表该随机变量取值的字母集。假定某函数
,将这些函数集中在一起形成函数集
,另外该函数集内函数的个数
与n无关。给定如下条件:
一定存在该变量中一个具体的数
,满足:
理解:如果经过函数变化后的随机变量的数学期望有上界,那么该函数的某些取值也有上界。
证明:
先做一个简单的改写,令,可以把
看成一个常数,根据联合界定理(union bound),来看一个很有意思的概率:
马上使用刚才谈到的Markov不等式,右边不就是某个变量大于某个数的概率,可得:
条件告诉我们:
直接带入可得:
推导这么久,无非是想说
翻译成人话就是。事件的概率小于1,也就是存在
。接下来就是计算复杂性理论很喜欢用到的一些转化。定理条件说
是有限的,也就是一个常数,并且该常数与n无关,常数在计算复杂性中可以忽略,所以可将
等效为
。
证明完毕。
简化理解:以上推导只是严格按照概率论格式来推导,所以看起来可能有点复杂。让我们来简化下。该定理说明当期望有上限时,至少存在一个变量的值也是这个上限(是不是很简单)。只不是今天的上限满足,(安全领域很喜欢研究渐近性)。
三. Chebyshev不等式
令X为随机变量,可得:
理解:变量的值与期望值不会相差太大,该上限与方差相关。
四. Chernov上限
4.1 变量大于
令X为随机变量,可得:
理解:将s看成一个常数,代表变量大于等于a的概率;
代表对变量操作指数变换
后,求数学期望;该定理反映了变量大于某值时对应的概率有上限,该上限与数学期望有关。与Markov不等式相比,多了一个s,在实际信息论安全推导时,可以设定任何自己想要的参数。
4.2 变量小于
令X为随机变量,可得:
该定理的理解与4.1类似,就不重复描述了。
相关文章:
信息论安全与概率论
目录 一. Markov不等式 二. 选择引理 三. Chebyshev不等式 四. Chernov上限 4.1 变量大于 4.2 变量小于 信息论安全中会用到很多概率论相关的上界,本文章将梳理几个论文中常用的定理,重点关注如何理解这些定理以及怎么用。 一. Markov不等式 假定…...
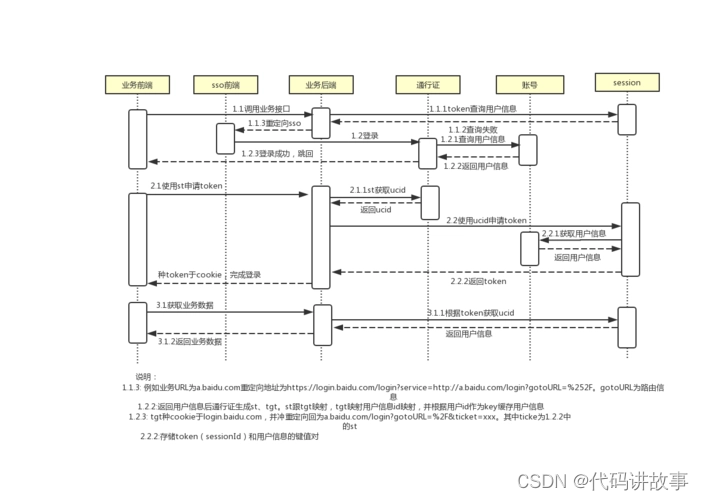
各种不同语言分别整理的拿来开箱即用的8个开源免费单点登录(SSO)系统
各种不同语言分别整理的拿来开箱即用的8个开源免费单点登录(SSO)系统。 单点登录(SSO)是一个登录服务层,通过一次登录访问多个应用。使用SSO服务可以提高多系统使用的用户体验和安全性,用户不必记忆多个密…...

Netty Review - 优化Netty通信:如何应对粘包和拆包挑战
文章目录 概述Pre概述场景复现解决办法概览方式一: 特殊分隔符分包 (演示Netty提供的众多方案中的一种)流程分析 方式二: 发送长度(推荐) DelimiterBasedFrameDecoder 源码分析 概述 Pre Netty Review - 借助SimpleTalkRoom初体验…...

vue介绍以及基本指令
目录 一、vue是什么 二、使用vue的准备工作 三、创建vue项目 四、vue插值表达式 五、vue基本指令 六、key的作用 七、v-model 九、指令修饰符 一、vue是什么 Vue是一种用于构建用户界面的JavaScript框架。它可以帮助开发人员构建单页应用程序和复杂的前端应用程序。Vue…...

重塑数字生产力体系,生成式AI将开启云计算未来新十年?
科技云报道原创。 今天我们正身处一个历史的洪流,一个巨变的十字路口。生成式AI让人工智能技术完全破圈,带来了机器学习被大规模采用的历史转折点。 它掀起的新一轮科技革命,远超出我们今天的想象,这意味着一个巨大的历史机遇正…...

JFreeChart 生成图表,并为图表标注特殊点、添加文本标识框
一、项目场景: Java使用JFreeChart库生成图片,主要场景为将具体的数据 可视化 生成曲线图等的图表。 本篇文章主要针对为数据集生成的图表添加特殊点及其标识框。具体包括两种场景:x轴为 时间戳 类型和普通 数值 类型。(y轴都为…...

vue整合axios 未完
一、简介 1、介绍 axios前端异步请求库类似jouery ajax技术,axios用来在前端页面发起一个异步请求,请求之后页面不动,响应回来刷新页面局部;Axios 是一个基于 promise 的 HTTP 库,可以用在浏览器和 node.js 中 2、特…...

java代码编写twitter授权登录
在上一篇内容已经介绍了怎么申请twitter开放的API接口。 下面介绍怎么通过twitter提供的API,进行授权登录功能。 开发者页面设置 首先在开发者页面开启“用户认证设置”,点击edit进行信息编辑。 我的授权登录是个网页,并且只需要进行简单的…...
SK Ecoplant借助亚马逊云科技,海外服务器为环保事业注入新活力
在当今全球面临着资源紧缺和环境挑战的大背景下,数字技术所依赖的海外服务器正成为加速循环经济转型的关键利器。然而,很多企业在整合数字技术到运营中仍然面临着一系列挑战,依然存在低效流程导致的不必要浪费。针对这一问题,SK E…...
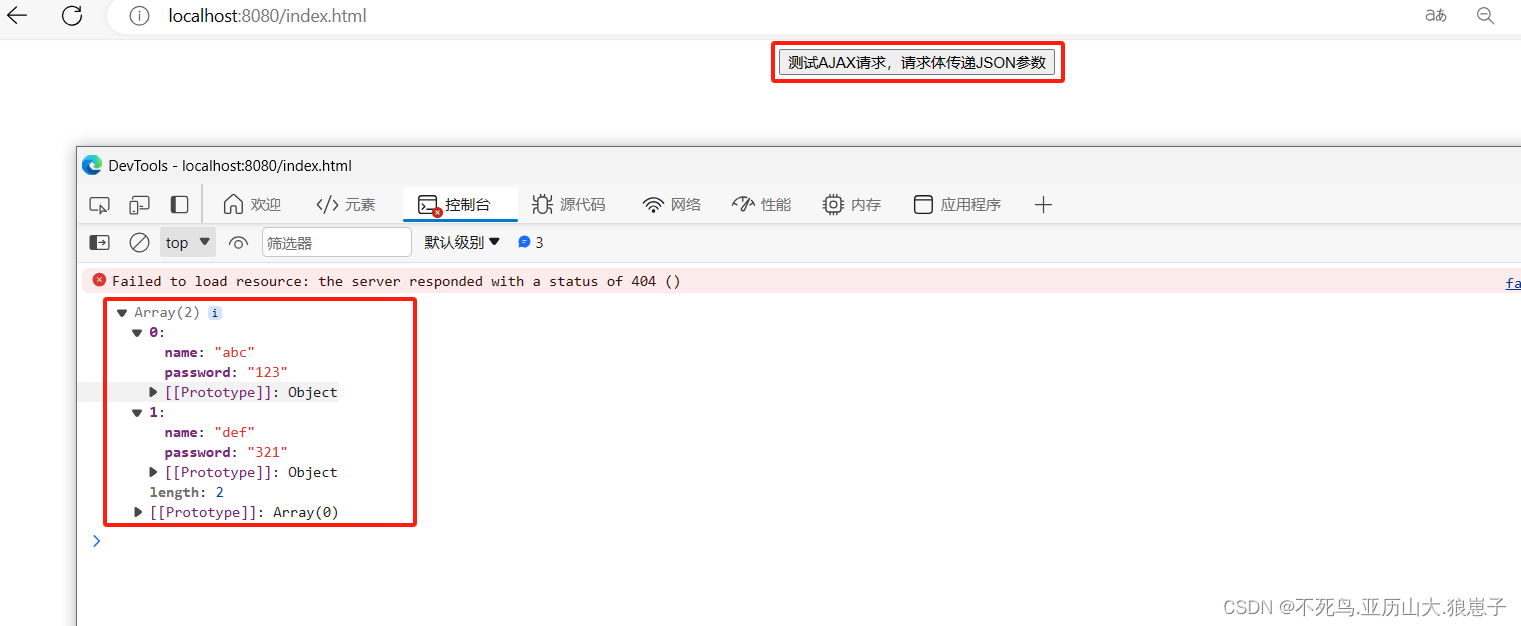
RPC(5):AJAX跨域请求处理
接上一篇RPC(4):HttpClient实现RPC之POST请求进行修改。 1 修改客户端项目 1.1 修改maven文件 修改后配置文件如下: <dependencyManagement><dependencies><dependency><groupId>org.springframework.b…...

用大白话举例子讲明白区块链
什么是区块链?网上这么说: 区块链是一种分布式数据库技术,它以块的形式记录和存储交易数据,并使用密码学算法保证数据的安全性和不可篡改性。每个块都包含了前一个块的哈希值和自身的交易数据,形成了一个不断增长的链条…...

Java URL
URL:统一资源定位符,说白了,就是一个网络 通过URLConnection类可以连接到URL,然后通过URLConnection可以获取读数据的通道。非文本数据用字节流来读取。 读完之后写入本地即可。 public class test {public static void main(S…...
:ETL涉及到的名词解释)
ETL-从1学到100(1/100):ETL涉及到的名词解释
本文章主要介绍ETL和大数据中涉及到名词,同时解释这些名词的含义。由于不是一次性收集这些名词,所以这篇文章将会持续更新,更新日志会存放在本段话下面: 12-19更新:OLTP、OLAP、BI、ETL。 12-20更新:ELT、…...

Jenkins + gitlab 持续集成和持续部署的学习笔记
1. Jenkins 介绍 软件开发生命周期(SLDC, Software Development Life Cycle):它集合了计划、开发、测试、部署的集合。 软件开发瀑布模型 软件的敏捷开发 1.1 持续集成 持续集成 (Continuous integration 简称 CI): 指的是频繁的将代码集成到主干。 持续集成的流…...

R语言【cli】——通过cli_abort用 cli 格式的内容显示错误、警告或信息,内部调用cli_bullets和inline-makeup
cli_abort(message,...,call .envir,.envir parent.frame(),.frame .envir ) 先从那些不需要下大力气理解的参数入手: 参数【.envir】:进行万能表达式编译的环境。 参数【.frame】:抛出上下文。默认用于参数【.trace_bottom】ÿ…...

cka从入门到放弃
无数次想放弃,最后选择了坚持 监控pod日志 监控名为 foobar 的 Pod 的日志,并过滤出具有 unable-access-website 信息的行,然后将 写入到 /opt/KUTR00101/foobar # 解析 监控pod的日志,使用kubectl logs pod-name kubectl logs…...

通过 jekyll 构建 github pages 博客实战笔记
jekyll 搭建教程 jekyll 搭建教程 Gem 安装 Ruby,请访问 下载地址。 Jekyll Jekyll 是一个简单且具备博客特性的静态网站生成器。 Jekyll 中文文档 极客学院中文文档 使用以下命令安装 Jekyll。 $ gem install jekyll在中国可能需要使用代理软件。然后ÿ…...

【AI美图】第09期效果图,AI人工智能汽车+摩托车系列图集
期待中的未来AI汽车 欢迎来到未来的世界,一个充满创新和无限可能的世界,这里有你从未见过的科技奇迹——AI汽车。 想象一下,你站在十字路口,繁忙的交通信号灯在你的视线中闪烁,汽车如潮水般涌来,但是&…...

网线的制作集线器交换机路由器的配置--含思维导图
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《产品经理如何画泳道图&流程图》 ⛺️ 越努力 ,越幸运 一、网线的制作 1、网线的材料有哪些? 网线 网线是一种用于传输数据信号的电缆,广泛应…...

LLM微调(四)| 微调Llama 2实现Text-to-SQL,并使用LlamaIndex在数据库上进行推理
Llama 2是开源LLM发展的一个巨大里程碑。最大模型及其经过微调的变体位居Hugging Face Open LLM排行榜(https://huggingface.co/spaces/HuggingFaceH4/open_llm_leaderboard)前列。多个基准测试表明,就性能而言,它正在接近GPT-3.5…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
