day38|70. 爬楼梯(进阶)、322. 零钱兑换、279.完全平方数
70. 爬楼梯(进阶)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
问题分析:
1、确定dp数组以及下标的含义
dp[j]:爬到 j 阶有多少种方法
2、确定递推公式
完全背包,重复利用物品,且为排列数
楼顶为背包,每次爬的阶数为物品
所以递推公式为:
dp[j]=dp[j]+dp[j-i]
3、dp数组初始化
初始化dp[0]=1
4、确定遍历顺序
本题要求是排列数,{2,1}和{1,2}是两种方法,所以先遍历背包。列排序中,阶数1和阶数2都在同层出现,所以会出现{1,2}和{2,1},为排列数
5、打印dp数组
class Solution {public int climbStairs(int n) {int[] dp=new int[n+1];dp[0]=1;for (int j=0;j<=n;j++){for (int i=1;i<=2;i++){if (j>=i) {dp[j] = dp[j] + dp[j - i];}}}return dp[n];}
}322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
问题分析:
1、确定dp数组以及下标的含义
dp[j]:装满 j 的最少物品是dp[j]
2、确定递推公式
金额为背包,硬币为物品
选出最少的物品数,用min方法,比较上一个物品的dp[j]和需要凑齐本次的物品数+1
所以递推公式为:
dp[j]=Math.min(dp[j],dp[j-coins[i]]+1)
3、dp数组初始化
初始化dp[0]=0,非0初始化为Integer.MAX_VALUE,因为递推公式为选出最小值,防止被覆盖应该先初始化一个最大值。
4、确定遍历顺序
本题为组合数,先遍历物品,再遍历背包
5、打印dp数组
class Solution {public int coinChange(int[] coins, int amount) {int[] dp=new int[amount+1];for (int j=0;j<=amount;j++){dp[j]=Integer.MAX_VALUE;}dp[0]=0;for (int i=0;i<coins.length;i++){for (int j=coins[i];j<=amount;j++){if (dp[j-coins[i]]!=Integer.MAX_VALUE) {//避免出现面额凑不齐总金额的情况// 需要凑齐的前一步也无法凑齐//导致这一步也无法凑齐// 例如[2] 3dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}/* for (int i=0;i<coins.length;i++){for (int j=0;j<=amount;j++){System.out.print(dp[j]+" ");}System.out.println("\n");}*/if (dp[amount]==Integer.MAX_VALUE) return -1;return dp[amount];}
}279.完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
问题分析:
1、确定dp数组以及下标的含义
dp[j]:组成和为n的最少的平方和数有dp[j]个
2、确定递推公式
和为背包,数字为物品
每个物品都是平方和数,即为i*i
选出最少的物品数,用min方法,比较上一个物品的dp[j]和需要凑齐本次的物品数+1
所以递推公式为:
dp[j]=Math.min(dp[j],dp[j-i*i]+1)
3、dp数组初始化
初始化dp[0]=0,非0初始化为Integer.MAX_VALUE,因为递推公式为选出最小值,防止被覆盖应该先初始化一个最大值。
4、确定遍历顺序
本题为组合数,先遍历物品,再遍历背包
5、打印dp数组
class Solution {public int numSquares(int n) {int[] dp=new int[n+1];for (int j=0;j<=n;j++){dp[j]=Integer.MAX_VALUE;}dp[0]=0;for (int i=1;i*i<=n;i++){for (int j=i*i;j<=n;j++){dp[j]=Math.min(dp[j],dp[j-i*i]+1);}}/*for (int i=1;i*i<=n;i++){for (int j=1;j<=n;j++){System.out.print(dp[j]+" ");}System.out.println("\n");}*/return dp[n];}
}
相关文章:
、322. 零钱兑换、279.完全平方数)
day38|70. 爬楼梯(进阶)、322. 零钱兑换、279.完全平方数
70. 爬楼梯(进阶) 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 示例 1: 输入:n 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 1 阶 2. 2…...
SpringBoot全局异常处理
一、目的 当客户端/前端向服务端发送一个请求后,这个请求并不是每次都能完全正确的处理,比如出现一些资源不存在、参数错误或者内部错误等信息的时候,就需要将异常反馈给客户端或者前端。那么这就需要程序有完整的异常处理机制。 在 Java 中所…...

SpringBoot异常处理
目录 一、 错误处理 1. 默认规则 2. 定制错误处理逻辑 二、自定义异常处理 1. 实现 ErrorController 2. RestControllerAdvice/ControllerAdvice ExceptionHandler 实现自定义异常 3. 新建 UserController.class 测试 3 种不同异常的处理 4. 最终效果如下 补充 1. 参…...
《C++ Primer Plus》(第6版)第8章编程练习
《C Primer Plus》(第6版)第8章编程练习《C Primer Plus》(第6版)第8章编程练习1. 打印字符串2. CandyBar3. 将string对象的内容转换为大写4. 设置并打印字符串5. max5()6. maxn()7. SumArray()《C Primer Plus》(第6版…...

RAD Studio 11.3 Alexandria Crack
RAD Studio 11.3 Alexandria Crack 瞄准最新平台版本-此版本增加了对Android 13和Apple macOS Ventura的官方支持。它还支持Ubuntu 22 LTS和Microsoft Windows Server 2022。 使用生物特征认证-New为FireMonkey移动应用程序提供了新的移动生物特征认证组件。 部署嵌入式InterBa…...

Stm32 iic 协议使用
/* 第1个参数为I2C操作句柄 第2个参数为从机设备地址 第3个参数为从机寄存器地址 第4个参数为从机寄存器地址长度 第5个参数为发送的数据的起始地址 第6个参数为传输数据的大小 第7个参数为操作超时时间 */ HAL_I2C_Mem_Write(&hi2c2,salve_add,0,0,PA_BUFF,sizeof(PA_BUFF…...
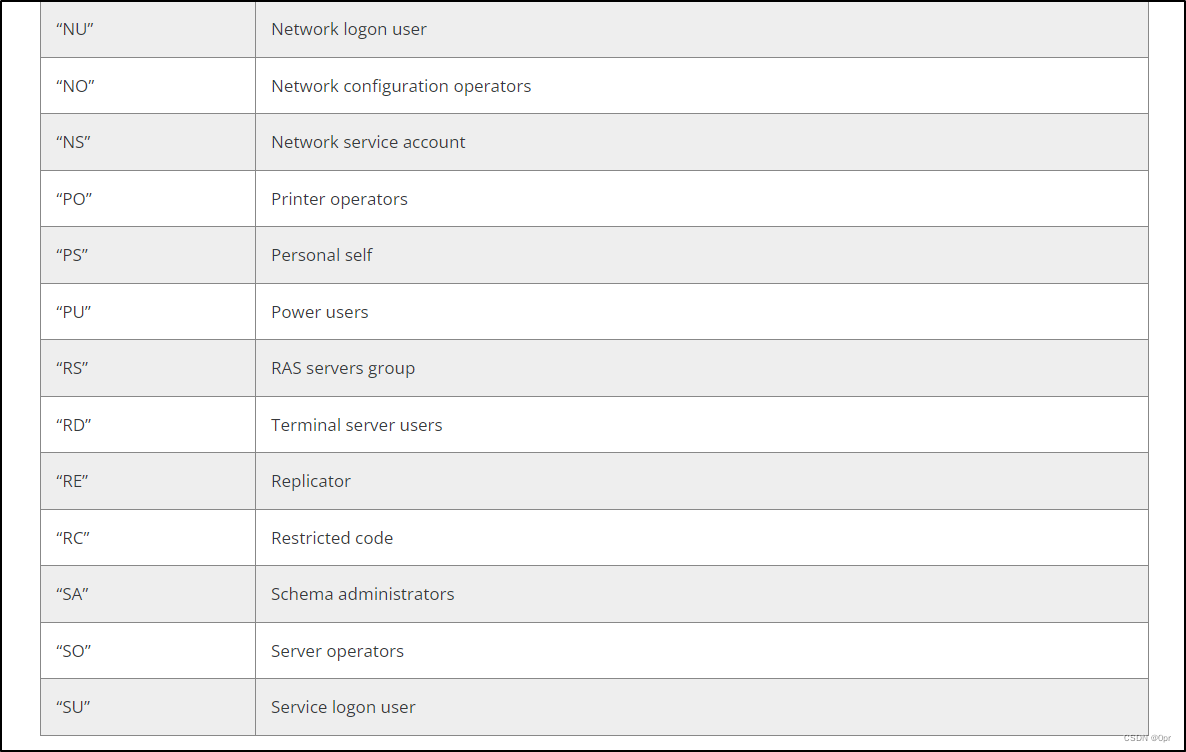
Malware Dev 02 - Windows SDDL 后门利用之 SCManager
写在最前 如果你是信息安全爱好者,如果你想考一些证书来提升自己的能力,那么欢迎大家来我的 Discord 频道 Northern Bay。邀请链接在这里: https://discord.gg/9XvvuFq9Wb我拥有 OSCP,OSEP,OSWE,OSED&…...

每日一题29——山峰数组的顶部
符合下列属性的数组 arr 称为 山峰数组(山脉数组) : arr.length > 3 存在 i(0 < i < arr.length - 1)使得: arr[0] < arr[1] < ... arr[i-1] < arr[i] arr[i] > arr[i1] > ... &g…...

Linux- 系统随你玩之--好用到炸裂的系统级监控、诊断工具
文章目录1、前言2、lsof介绍2.1、问题来了: 所有用户都可以采用该命令吗?3、 服务器安装lsof3.1、安装3.2、检查安装是否正常。4、lsof 命令4.1、常用功能选项4.2、输出内容4.2.1 、FD和 TYPE列5、 lsof 命令实操常见用法6 、常用组合命令7、 结语1、前言…...
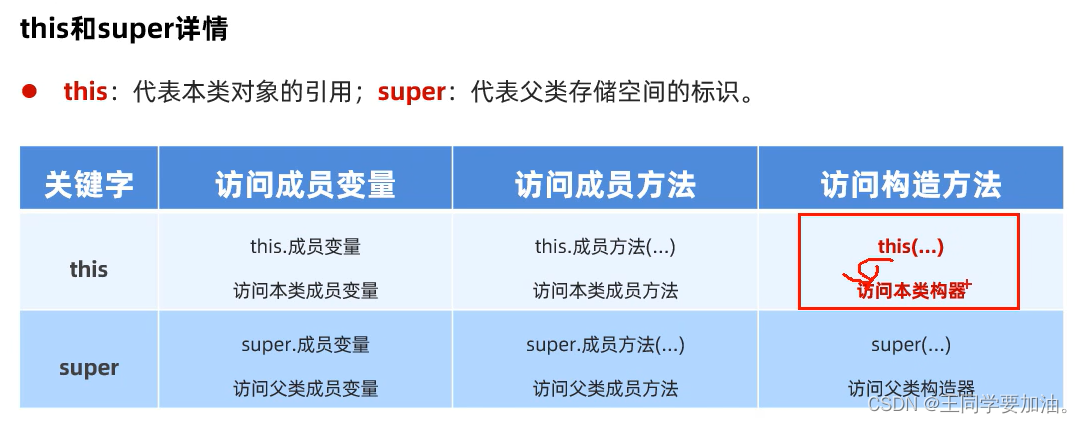
第十三节 继承
什么是继承? java中提供一个关键字extends,用这个关键字,我们可以让一个类和另一个类建立父子关系。 public class Student extends People{} student为子类(派生类),people为父类(基类或者超类…...

【优化】性能优化Springboot 项目配置内置Tomcat使用Http11AprProtocol(AIO)
Springboot 项目配置内置tomcat使用Http11AprProtocol(AIO) Windows版本 1.下载Springboot对应版本tomcat包 下载地址 Apache Tomcat - Apache Tomcat 9 Software Downloads 找到bin目录下 tcnative-1.dll 文件 2 放到jdk的bin目录下 Linux版本 在Springboot中内嵌的Tomcat默…...
SpringBoot之@ConfigurationProperties、@EnableConfigurationProperties
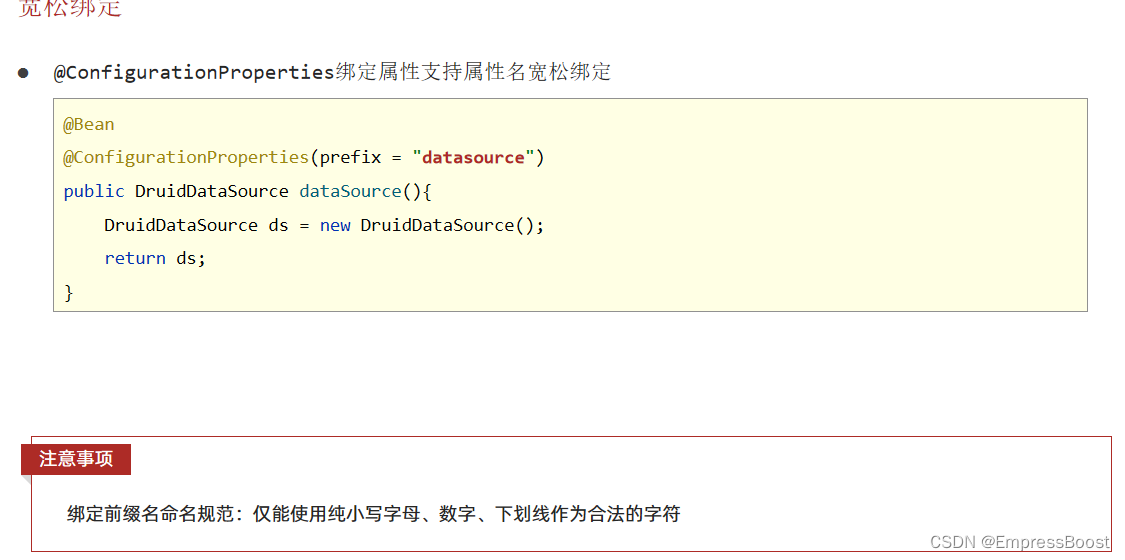
ConfigurationProperties 这个注解不仅可以为yml某个类注入还可以为第三方bean绑定属性 为yml某个类注入 只要将对应的yml类对象声明实体pojo并交给spring容器管理,再在类上使用ConfigurationProperties绑定对应的类名即可 涉及到两个知识点,这个类对…...
数组一次性删除多条数据
需求描述 最后提交时删除表格中的空行 实现方法 单行删除 - 并不是一次性删除 表格每行的最后设置删除按钮,点击时将当前行的索引传递给方法,splice 删除当前行。 <el-table :data"tableData" class"myTable" border>..…...

相机删除照片如何恢复?一键解决它
相机删除照片如何恢复?喜欢用相机拍照的人,总会在空闲时多拍几张,这使我们相机中会储存大量的、各种各样的照片。等到回家后,在进行删除,并选出比较好的照片。但也很容易就误删了一些好看的照片。碰到这种意外事&#…...

vue3搭建教程(基于webpack+create-vue+ element-plus)
前言使用vue脚手架搭建vuetswebpack项目搭建步骤:下载node 版本可以 12 或者14或者 16.0,此次使用的>16.0版本,vue-cli通过npm i -g vue/cli 升级到了 vue cli v5.0.8建目录,如(vue3Study)用IDE工具打开…...

代码随想录算法训练营第四十二天 | leetcode 1049. 最后一块石头的重量 II,494. 目标和,474.一和零
代码随想录算法训练营第四十二天 | leetcode 1049. 最后一块石头的重量 II,494. 目标和,474.一和零1049. 最后一块石头的重量 II494. 目标和474.一和零1049. 最后一块石头的重量 II 题目: 有一堆石头,每块石头的重量都是正整数。…...

Java8中Lambda表达式之Collection 的常见用法
背景 在java8中引入了Lambda表达式。其实,他就是一个匿名函数。我们经常会用到一些循环遍历,起始完全就可以通过Lambda来简化我们不必要的操作,下面我们来看一下Lambda常用的方法。 准备条件 DataBuilderprivate static class Person {priv…...
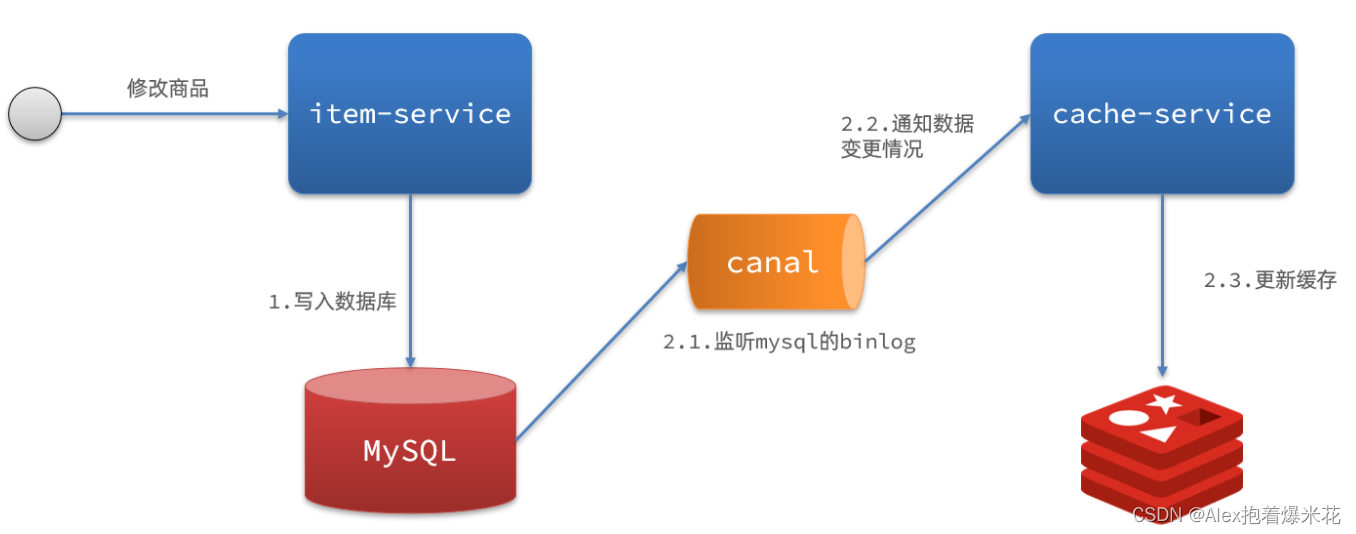
SpringCloud系列知识快速复习 -- part 2(Sentinel微服务保护,Seata分布式事务,Redis分布式缓存和多级缓存)
SpringCloud系列知识快速复习 -- part 2(Sentinel微服务保护,Seata分布式事务,Redis分布式缓存和多级缓存Sentinel微服务保护什么是雪崩问题?解决方法服务保护技术对比流量控制簇点链路Sentinel流控模式流控效果热点参数限流隔离和…...
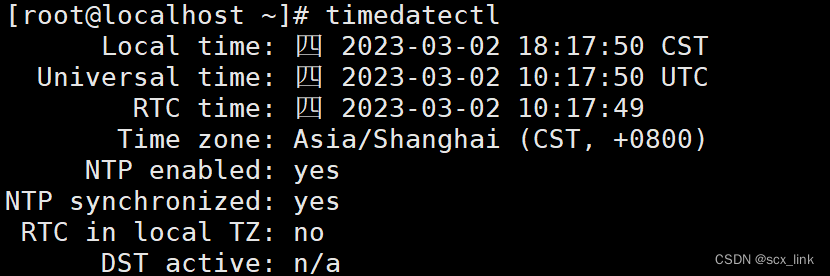
设置CentOS7的时间与网络同步
1.设置时区为北京时间 [rootlocalhost ~]# timedatectl set-timezone Asia/Shanghai 2.查看系统时间 [rootlocalhost ~]# timedatectl Local time: 四 2023-03-02 17:40:41 CST #系统时间 Universal time: 四 2023-03-02 09:40:41 UTC …...

java开发手册之编程规约
文章目录编程规约命名风格常量定义代码格式OOP规约集合处理并发处理控制语句注释规约其它编程规约 命名风格 1.代码中的命名均不能以下划线或者美元符号开始,也不能以下划线或者美元符号结束 例如:_name | name__ | name$ | $name2.代码中的命名严…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
