ARC142E Pairing Wizards
ARC142E Pairing Wizards
题目大意
有nnn个法师,编号为111到nnn。法师iii有强度aia_iai,他计划打败强壮度为bib_ibi的怪物。
你可以执行以下操作任意次:
- 选中一个法师,将它的强壮度增加1
一对法师(i,j)(i,j)(i,j)称为好的,当至少满足以下条件之一:
- 法师iii至少有bib_ibi的强壮度,法师jjj至少有bjb_jbj的强壮度
- 法师iii至少有bjb_jbj的强壮度,法师jjj至少有bib_ibi的强壮度
你的目标是对于i=1,…,mi=1,\dots,mi=1,…,m,使得(xi,yi)(x_i,y_i)(xi,yi)称为一对好的法师。求最小的操作数量。
题解
首先,令mnx=max(x,y)∈E(min(bx,by))mn_x=\max\limits_{(x,y)\in E}(\min(b_x,b_y))mnx=(x,y)∈Emax(min(bx,by))。如果ax<mnxa_x<mn_xax<mnx,则不断增加axa_xax使得ax=mnxa_x=mn_xax=mnx。
如果bx>axb_x>a_xbx>ax,则xxx属于XXX集合;如果bx≤axb_x\leq a_xbx≤ax,则xxx属于YYY集合。我们把每一对法师看作一条边,因为上面对axa_xax的改变,所以每条边中至少有一个点在YYY集合中。
每个XXX集合的点xxx对应一个点xxx,每个YYY集合中的点yyy和一个在1到100之间的值aaa对应一个点(y,a)(y,a)(y,a)。我们可以按如下方法建图,那么答案为最小割,即最大流,用网络流即可解决。
- 对于i∈Xi\in Xi∈X,连边(s,i,bi−ai)(s,i,b_i-a_i)(s,i,bi−ai)
- 对于i∈Yi\in Yi∈Y,连边((i,j),t,1)((i,j),t,1)((i,j),t,1)
- 对于i∈Yi\in Yi∈Y,连边((i,j),(i,j−1),∞)((i,j),(i,j-1),\infty)((i,j),(i,j−1),∞)
- 对于(i,j)∈E,i∈X,j∈Y,bi>aj(i,j)\in E,i\in X,j\in Y,b_i>a_j(i,j)∈E,i∈X,j∈Y,bi>aj,连边(i,(j,bi−aj),∞)(i,(j,b_i-a_j),\infty)(i,(j,bi−aj),∞)
如果要使ax≥bxa_x\geq b_xax≥bx,则割第一类边;如果要使ax≥by,ay≥bxa_x\geq b_y,a_y\geq b_xax≥by,ay≥bx,则割第二类边。因为无限的影响,第三类边只能将jjj值小的放在sss的一边,jjj值大的放在ttt的一边,第四类边不会被割。这样就可以求最小的操作数了。
code
#include<bits/stdc++.h>
using namespace std;
int n,m,x,y,ans=0,vt=0,s,t,v1=0,v2=0,inf=1e9,a[105],b[105],mn[105],on[105],re[105];
int tot=1,cs[100005],l[100005],r[100005],w[100005],d[100005],vd[100005];
struct node{int x,y;
}vw[10005];
void add(int xx,int yy,int zz){l[++tot]=r[xx];cs[tot]=yy;r[xx]=tot;w[tot]=zz;
}
int aug(int i,int augco){if(i==t) return augco;int augc=augco,dl=0,md=n-1;for(int u=r[i];u;u=l[u]){int j=cs[u];if(w[u]>0){if(d[i]==d[j]+1){dl=min(augc,w[u]);dl=aug(j,dl);w[u]-=dl;w[u^1]+=dl;augc-=dl;if(d[s]>=n) return augco-augc;if(!augc) break;}if(md>d[j]) md=d[j];}}if(augco==augc){--vd[d[i]];if(!vd[d[i]]) d[s]=n;d[i]=md+1;++vd[d[i]];}return augco-augc;
}
void sap(){vd[0]=n;while(d[s]<n) ans+=aug(s,inf);
}
int main()
{scanf("%d",&n);s=++vt;t=++vt;for(int i=1;i<=n;i++){scanf("%d%d",&a[i],&b[i]);mn[i]=a[i];}scanf("%d",&m);for(int i=1;i<=m;i++){scanf("%d%d",&x,&y);vw[i]=(node){x,y};mn[x]=max(mn[x],min(b[x],b[y]));mn[y]=max(mn[y],min(b[x],b[y]));}for(int i=1;i<=n;i++){ans+=mn[i]-a[i];a[i]=mn[i];if(a[i]<b[i]){add(s,i+2,b[i]-a[i]);add(i+2,s,0);}else{re[i]=++v2;on[i]=1;for(int j=1;j<=100;j++){add(2+n+(i-1)*100+j,t,1);add(t,2+n+(i-1)*100+j,0);if(j>1){add(2+n+(i-1)*100+j,2+n+(i-1)*100+j-1,inf);add(2+n+(i-1)*100+j-1,2+n+(i-1)*100+j,0);}}}}for(int i=1;i<=m;i++){x=vw[i].x;y=vw[i].y;if(on[x]==0&&on[y]==1){if(b[x]>a[y]){add(x+2,2+n+(y-1)*100+b[x]-a[y],inf);add(2+n+(y-1)*100+b[x]-a[y],x+2,0);}}else if(on[x]==1&&on[y]==0){swap(x,y);if(b[x]>a[y]){add(x+2,2+n+(y-1)*100+b[x]-a[y],inf);add(2+n+(y-1)*100+b[x]-a[y],x+2,0);}}}n=2+n+n*100;sap();printf("%d",ans);return 0;
}
相关文章:

ARC142E Pairing Wizards
ARC142E Pairing Wizards 题目大意 有nnn个法师,编号为111到nnn。法师iii有强度aia_iai,他计划打败强壮度为bib_ibi的怪物。 你可以执行以下操作任意次: 选中一个法师,将它的强壮度增加1 一对法师(i,j)(i,j)(i,j)称为好的…...

Spark开发实战-主播打赏排行榜统计
(一)需求分析 计算每个大区当天金币收入排名前N的主播 背景: 我们有一款直播APP,已经在很多国家上线并运营了一段时间,产品经理希望开发一个功能,计算前N主播排行榜,按天更新排名信息…...

python 如何存储数据 (python 的文件和异常)
文章目录存储数据1. 使用 json.dump() 和 json.load()json.dump()2. 保存和读取用户生成的数据存储数据 很多程序都要求用户输入某种信息,如让用户存储游戏首选项或提供要可视化的数据。不管专注的是什么,程序都把用户提供的信息存储在列表和字典等数据结…...

第三章-OpenCV基础-8-绘图函数
前置内容 这篇内容不是本书内容,但后续用的到,特做记录。 使用OpenCV中不可避免需要用到各种绘图功能,比如绘制人脸库、显示人脸识别信息,那就需要用到OpenCV的绘图函数,这些函数包括cv2.line(), cv2.circle(),cv2.rectangle()…...
逆约瑟夫问题
约瑟夫问题可以说十分经典,其没有公式解也是广为人知的~ 目录 前言 一、约瑟夫问题与逆约瑟夫问题 1.约瑟夫问题 2.逆约瑟夫问题 二、思考与尝试(显然有很多失败) 问题分析 尝试一:递归/递推的尝试 尝试二:条件…...
)
MySQL之三大日志(更新中)
MySQL之三大日志(更新中) MySQL日志记录着数据库运行过程中的各种信息,包括:错误日志、普通查询日志、慢查询日志、二进制日志、中继日志、事务日志等。 综合上一篇《MySQL之"幻读"问题》涉及到事务,本文主…...

如何使用EvilTree在文件中搜索正则或关键字匹配的内容
关于EvilTree EvilTree是一款功能强大的文件内容搜索工具,该工具基于经典的“tree”命令实现其功能,本质上来说它就是“tree”命令的一个独立Python 3重制版。但EvilTree还增加了在文件中搜索用户提供的关键字或正则表达式的额外功能,而且还…...

北京移动CM311-5s-ZG_GK6323V100C_2+8_免拆一键卡刷固件包
北京移动CM311-5s-ZG_GK6323V100C_28_免拆一键卡刷固件包 特点: 1、适用于对应型号的电视盒子刷机; 2、开放原厂固件屏蔽的市场安装和u盘安装apk; 3、修改dns,三网通用; 4、大量精简内置的没用的软件,…...

JavaScript(1)
JavaScript简介 JavaScript是一门跨平台、面向对象的脚本语言,用来控制网页行为的,它能使网页可以交互。 JavaScript引入方式 1、内部脚本 将js代码定义在HTML页面中,在HTML中,JavaScript代码必须位于<script>与</scrip…...

阿里云云原生每月动态 | 聚焦实战,面向开发者的系列课程全新上线
作者:云原生内容小组 云原生是企业数字创新的最短路径。 《阿里云云原生每月动态》,从趋势热点、产品新功能、服务客户、开源与开发者动态等方面,为企业提供数字化的路径与指南。 本栏目每月更新。 趋势热点 《云原生实战指南》白皮书发布 …...

Goby 征文大擂台,超值盲盒等你来!
001 Goby 技术征文正式启动 Goby 致力于做最好的网络安全工具。为了促进师傅们知识共享和技术交流,现发起关于 Goby 的技术文章征集活动! 欢迎所有师傅们参加,分享您的使用经验或挖洞窍门等,帮助其他人更好地了解和利用 Goby。 …...

NLP - langid 语种识别
文章目录一、关于 langid二、基本使用Normalization多个语言中选择一个三、训练模型1、需要2、工具是3、过程4、代码调用自定义模型一、关于 langid https://github.com/saffsd/langid.py 用于检测语言 二、基本使用 import langidlangid.classify("This is a test"…...

liquibase学习和使用
文章目录liquibase学习介绍数据库更新日志和数据库更新日志锁定相关概念changelogchangeset的属性preconditionsql样例Contextssql样例Labelsql样例文件格式sql样例其他格式用的时候在补充跟踪表DATABASECHANGELOGLOCK (数据库更改日志锁定表)DATABASECH…...
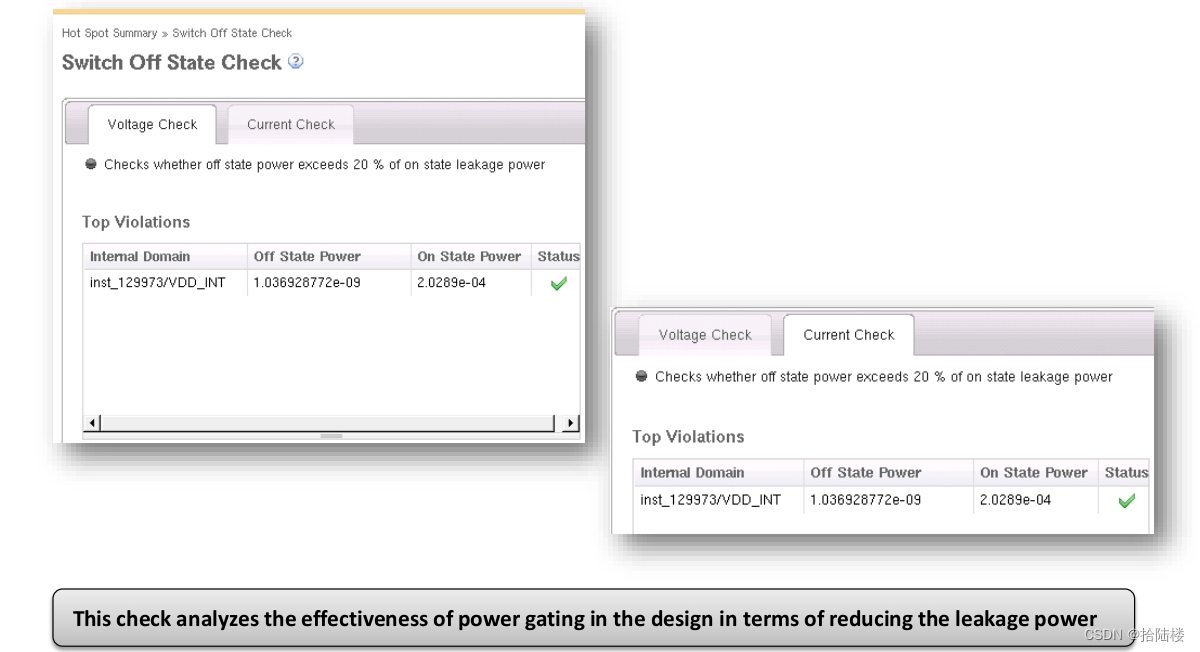
redhawk:Low Power Analysis
1.rush current与switch cell 在standby状态下为了控制leakage power我们选择power gating的设计方式,使用power switch cell关闭block/power domain的电源。 power switch的基本介绍可见: 低功耗设计-Power Switch power switch的table中有四种状态,…...

24- 深度学习的模型保存和加载 (TensorFlow系列) (深度学习)
知识要点 keras 保存成hdf5文件, 1.保存模型和参数, 2.只保存参数 1.保存模型和参数 save_modelcallback ModelCheckpoint2. 只保存参数 save_weightscallback ModelCheckpoint save_weights_only True 保存模型: 案例数据: Fashion-MNIST总共有十个类别的图像model.save_w…...

【Echarts图例点击事件】自定义Echarts图例legend点击事件(已解决)
目录先睹为快(效果)1、实现Echarts多条曲线2、点击echarts触发接口请求2.1 先默认隐藏部分数据2.2 自定义legend图例点击事件3、源码下载地址(解压即用)**【写在前面】**这下我又不得不说了,还是客户现场使用时想查询一…...

uniapp-首页配置
为了获取到后台服务器发来的数据,需要配置相应的网络地址。位置在main.js入口文件中。 import { $http } from escook/request-miniprogramuni.$http $http // 配置请求根路径 $http.baseUrl https://api-hmugo-web.itheima.net// 请求开始之前做一些事情 $http.…...

支持DDR5,超频更简单,小雕够给力,技嘉B760M小雕WIFI主板上手
目前13代酷睿已经全员集结了,其中全新的i5 13490F应该依然会备受欢迎,当然了,刚上市不久的13代酷睿价格方面还不是很有吸引力,好在12代酷睿在新一代主板上面依然可用,所以预算有限的朋友,完全可用继续使用1…...
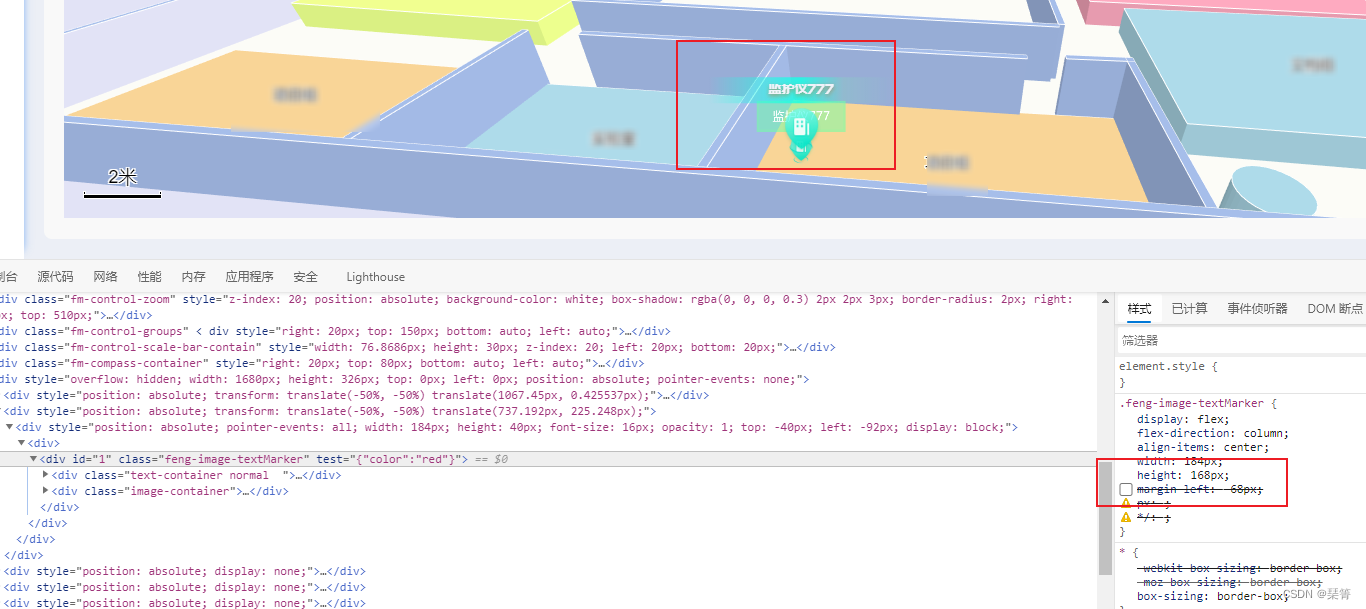
fengMap 自定义dom 偏离实际位置;缩放时飘出地图所在区域
目录 一、问题 二、原因及解决方法 三、总结 一、问题 1.前人写了一份代码,很奇怪。使用 new fengmap.FMCompositeMarker添加的复合覆盖物位置是正常的,缩放的时候也是正常的,仍然处于地图内部;但是new fengmap.FMDomMarker添加…...
TryHackMe-黑我杯
黑我杯 相信我们大家在TryHackMe的日积月累都学到了不少东西,从纯萌新到oscp再到更高 我很高兴能将国内各thm玩家聚集到一起,构建一个更好的学习环境和氛围 本次娱乐分两场: Offensive Pentesting — 中等难度Junior Penetration — 容易难…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
