剑指 Offer 16. 数值的整数次方
摘要
剑指 Offer 16. 数值的整数次方
本题的方法被称为快速幂算法,有递归和迭代两个版本。这篇题解会从递归版本的开始讲起,再逐步引出迭代的版本。当指数n为负数时,我们可以计算 x^(-n)再取倒数得到结果,因此我们只需要考虑n为自然数的情况。
一:快速幂 + 递归
快速幂算法的本质是分治算法。举个例子,如果我们要计算x^64,我们可以按照:
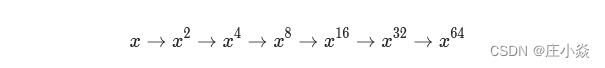
的顺序,从x开始,每次直接把上一次的结果进行平方,计算6次就可以得到 x^(64)的值,而不需要对 x乘 63次x。再举一个例子,如果我们要计算 x^77,我们可以按照:
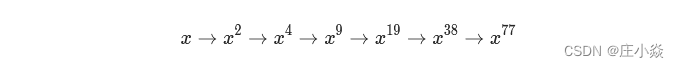
的顺序,在 x→x^2,x2→x^4,x19→x^38 这些步骤中,我们直接把上一次的结果进行平方,而在 x4→x^9,x9→x19,x38→x77这些步骤中,把上一次的结果进行平方后,还要额外乘一个 x。直接从左到右进行推导看上去很困难,因为在每一步中,我们不知道在将上一次的结果平方之后,还需不需要额外乘 xx。但如果我们从右往左看,分治的思想就十分明显了:
- 当我们要计算 x^n时,我们可以先递归地计算出 y=x⌊n/2⌋,其中⌊a⌋表示对a进行下取整;
- 根据递归计算的结果,如果 n为偶数,那么 x^n=y^2;如果n为奇数,那么 x^n=y^2×x;
- 递归的边界为n=0,任意数的0次方均为1。
由于每次递归都会使得指数减少一半,因此递归的层数为 O(logn),算法可以在很快的时间内得到结果。
class Solution {public double myPow(double x, int n) {long N = n;return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);}public double quickMul(double x, long N) {if (N == 0) {return 1.0;}double y = quickMul(x, N / 2);return N % 2 == 0 ? y * y : y * y * x;}
}复杂度分析
- 时间复杂度:O(logn),即为递归的层数。
- 空间复杂度:O(logn),即为递归的层数。这是由于递归的函数调用会使用栈空间。
二、快速幂 + 迭代
由于递归需要使用额外的栈空间,我们试着将递归转写为迭代。在方法一中,我们也提到过,从左到右进行推导是不容易的,因为我们不知道是否需要额外乘x。但我们不妨找一找规律,看看哪些地方额外乘了x,并且它们对答案产生了什么影响。


class Solution {public double myPow(double x, int n) {long N = n;return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);}public double quickMul(double x, long N) {double ans = 1.0;// 贡献的初始值为 xdouble x_contribute = x;// 在对 N 进行二进制拆分的同时计算答案while (N > 0) {if (N % 2 == 1) {// 如果 N 二进制表示的最低位为 1,那么需要计入贡献ans *= x_contribute;}// 将贡献不断地平方x_contribute *= x_contribute;// 舍弃 N 二进制表示的最低位,这样我们每次只要判断最低位即可N /= 2;}return ans;}
}复杂度分析
-
时间复杂度:O(logn),即为对n进行二进制拆分的时间复杂度。
-
空间复杂度:O(1)。
博文参考
《leetcode》
相关文章:

剑指 Offer 16. 数值的整数次方
摘要 剑指 Offer 16. 数值的整数次方 本题的方法被称为快速幂算法,有递归和迭代两个版本。这篇题解会从递归版本的开始讲起,再逐步引出迭代的版本。当指数n为负数时,我们可以计算 x^(-n)再取倒数得到结果,因此我们只需要考虑n为…...
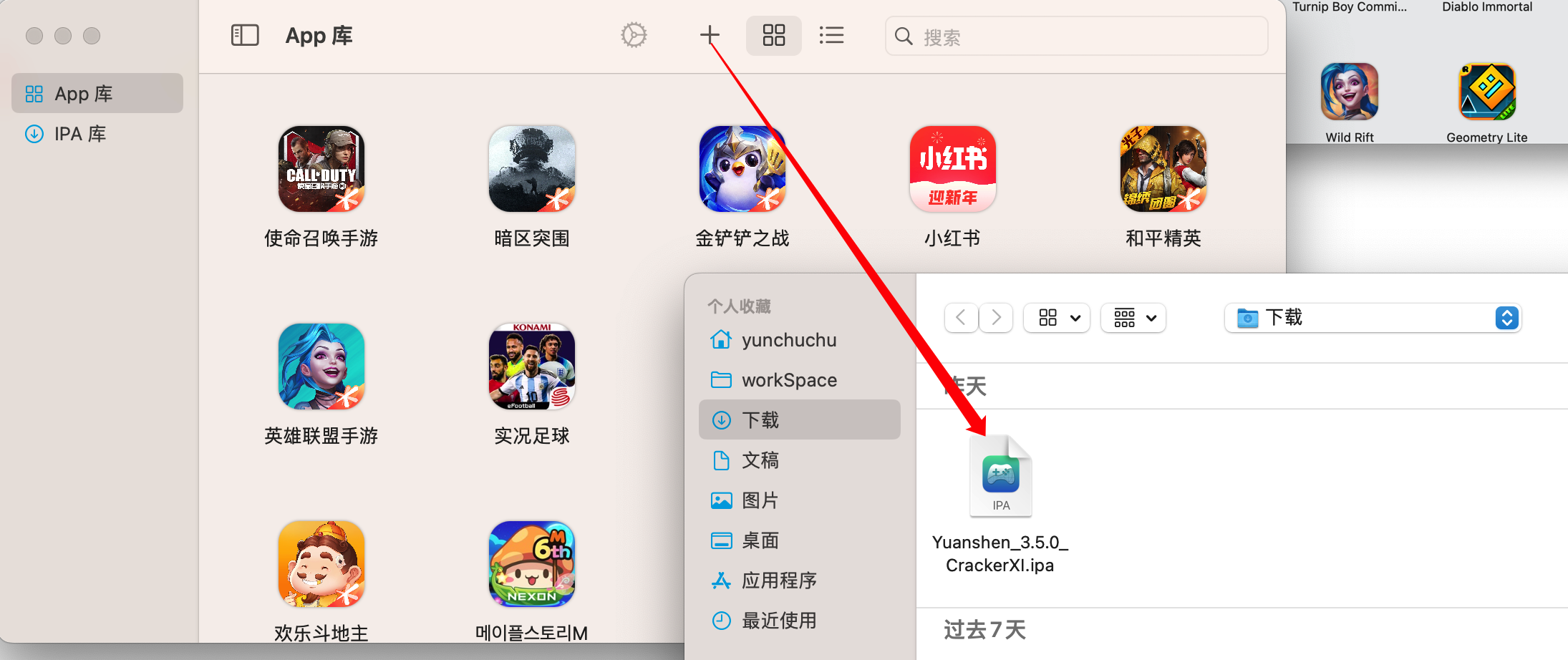
在苹果电脑 mac 上安装原神(playCover)
该方法只能在 M1、M2 mac 上安装原神 目录前言一、首先下载安装 playCover1. playCover 下载2. playCover 安装安装出现问题解决方法二、下载安装原神1.安装包下载2.安装原神三、登录、键盘映射及版本更新等问题登录键盘映射版本更新前言 最近买了新的mac,作者本人…...

数据结构考研习题精选
1 A假设比较t次,由于换或不换,则必然有2^t种可能。又设有n个关键字,n!排列组合,则必然有2^t&…...
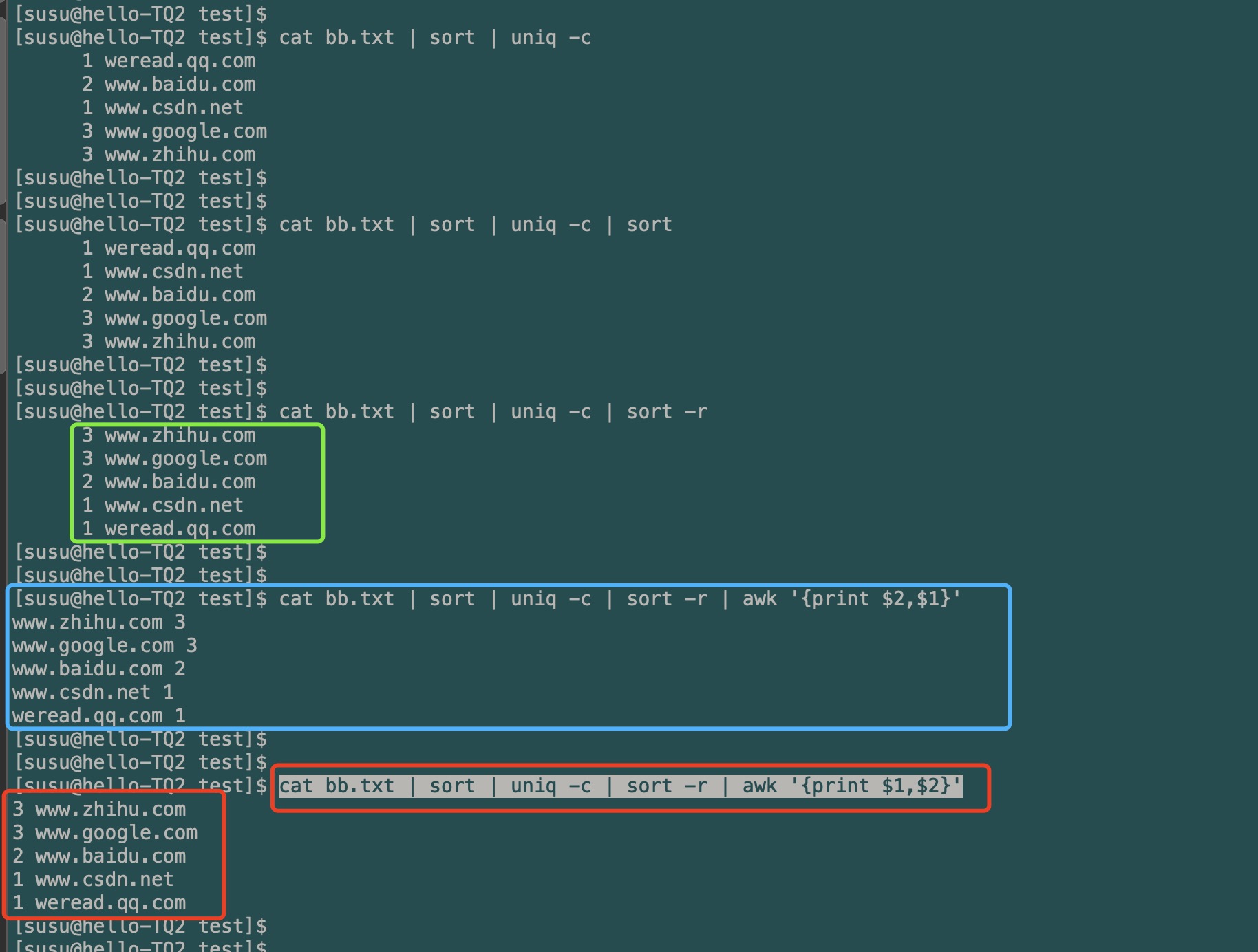
linux常用命令介绍 04 篇——uniq命令使用介绍(Linux重复数据的统计处理)
linux常用命令介绍 04 篇——uniq命令使用介绍(Linux重复数据的统计处理)1. uniq 使用语法2. sort 简单效果3. uniq 使用例子3.1 不加任何选项3.1.1 不用 sort 效果3.1.2 uniq 结合 sort 一起使用3.2 使用选项例子3.2.1 去重打印(或打印不重复…...
网站打不开数据库错误等常见问题解决方法
1、“主机开设成功!”上传数据后显示此内容,是因为西部数码默认放置的index.htm内容,需要核实wwwroot目录里面是否有自己的程序文件,可以删除index.htm。 2、恭喜,lanmp安装成功!这个页面是wdcp的默认页面&…...

爬虫实战进阶版【1】——某眼专业版实时票房接口破解
某眼专业版-实时票房接口破解 某眼票房接口:https://piaofang.maoyan.com/dashboard-ajax 前言 当我们想根据某眼的接口获取票房信息的时候,发现它的接口处的参数是加密的,如下图: 红色框框的参数都是动态变化的,且signKey明显是加密的一个参数。对于这种加密的参数,我们需要…...

大话数据结构-普里姆算法(Prim)和克鲁斯卡尔算法(Kruskal)
5 最小生成树 构造连通网的最小代价生成树称为最小生成树,即Minimum Cost Spanning Tree,最小生成树通常是基于无向网/有向网构造的。 找连通网的最小生成树,经典的有两种算法,普里姆算法和克鲁斯卡尔算法。 5.1 普里姆ÿ…...
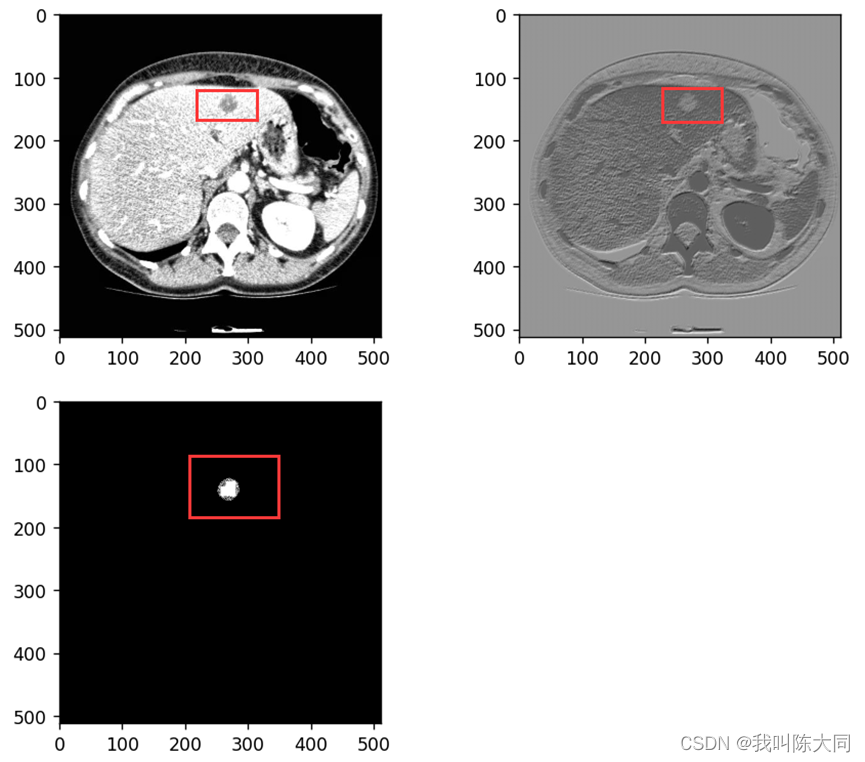
UNet-肝脏肿瘤图像语义分割
目录 一. 语义分割 二. 数据集 三. 数据增强 图像数据处理步骤 CT图像增强方法 :windowing方法 直方图均衡化 获取掩膜图像深度 在肿瘤CT图中提取肿瘤 保存肿瘤数据 四. 数据加载 数据批处理 编辑编辑 数据集加载 五. UNet神经网络模型搭建 单张图片…...

三周爆赚千万 电竞选手在无聊猿游戏赢麻了
如何用3个星期赚到1千万?普通人做梦都不敢想的事,电竞职业选手Mongraal却用几把游戏轻易完成,赚钱地点是蓝筹NFT项目Bored Ape Yacht Club(BAYC无聊猿)出品的新游戏Dookey Dash。 这款游戏类似《神庙逃亡》࿰…...

BERT学习
非精读BERT-b站有讲解视频(跟着李沐学AI) (大佬好厉害,讲的比直接看论文容易懂得多) 写在前面 在计算MLM预训练任务的损失函数的时候,参与计算的Tokens有哪些?是全部的15%的词汇还是15%词汇中真…...
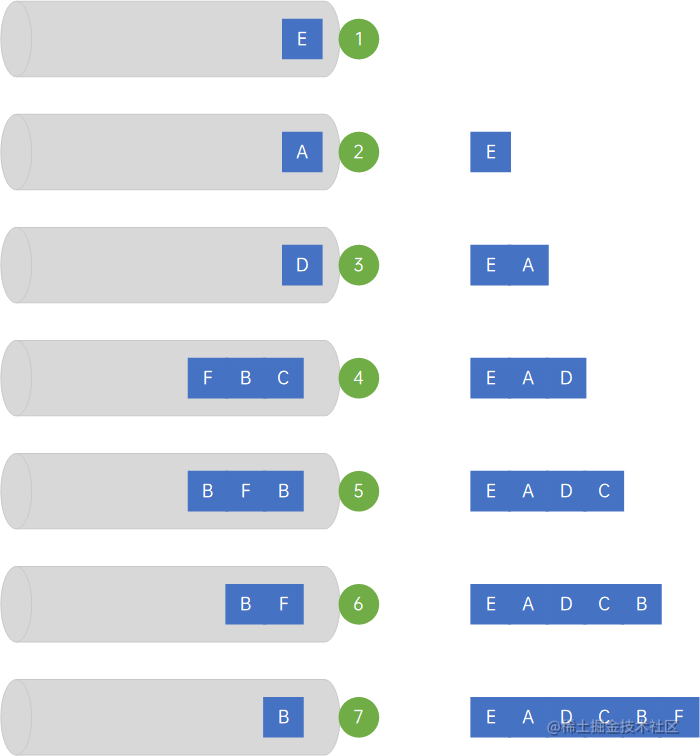
大话数据结构-图的深度优先遍历和广度优先遍历
4 图的遍历 图的遍历分为深度优先遍历和广度优先遍历两种。 4.1 深度优先遍历 深度优先遍历(Depth First Search),也称为深度优先搜索,简称DFS,深度优先遍历,是指从某一个顶点开始,按照一定的规…...

c语言指针怎么理解 第一部分
不理解指针,是因为有人教错了你。 有人告诉你,指针是“指向”某某某的,那就是误导你,给你挖了个坑。初学者小心不要误读这“指向”二字。 第一,“指针”通常用于保存一个地址,这个地址的数据类型在定义指…...
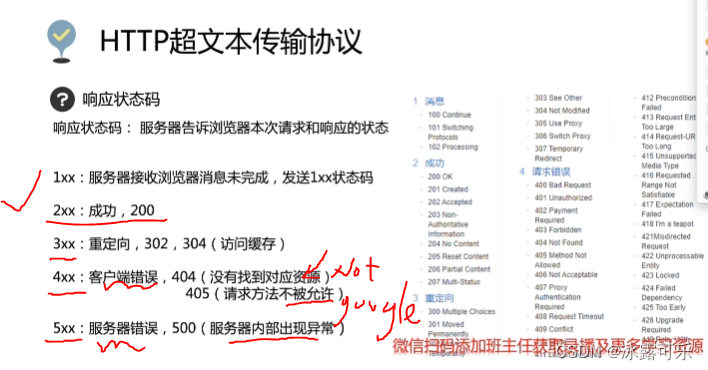
计算机网络安全基础知识2:http超文本传输协议,请求request消息的get和post,响应response消息的格式,响应状态码
计算机网络安全基础知识: 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,oracle,尤…...

Pytest自动化框架~权威教程03-原有TestSuite的执行方法
前言TestSuite一直是unittest的灵活与精髓之处, 在繁多的测试用例中, 可以任意挑选和组合各种用例集, 比如smoke用例集, level1用例集, webtest用例集, bug回归用例集等等, 当然这些TestSuite需要我们提前定义好, 并把用例加载进去.Pytest采取的是完全不同的用例组织和运行方式…...

web自动化 基于python+Selenium+PHP+Ftp实现的轻量级web自动化测试框架
1、 开发环境 win7 64 PyCharm 4.0.5 setuptools-29.0.1.zip 下载地址:setuptools-29.0.1.zip_免费高速下载|百度网盘-分享无限制 官方下载地址:setuptools PyPI python 3.3.2 mysql-connector-python-2.1.4-py3.3-win64 下载地址:mysq…...

【MyBatis】源码学习 05 - 关于 xml 文件解析的分析
文章目录前言参考目录学习笔记1、章节目录概览2、14.3:SqlSourceBuilder 类与 StaticSqlSource 类3、14.4.2:ResultMapResolver 类3.1、测试代码说明3.2、结果集 userMap 解析流程3.3、结果集 getGirl 解析流程3.4、鉴别器 discriminator 解析流程4、14.…...
代码随想录算法训练营第二天| 977. 有序数组的平方、209. 长度最小子数组、59.螺旋矩阵II
977 有序数组的平方题目链接:977 有序数组的平方介绍给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。思路看到题目的第一反应,首先负数的平方跟正数的平方是相同的&…...
Ethercat系列(10)用QT实现SOEM主站
首先将SOEM编译成静态Lib库可以参考前面的博文(83条消息) VS2017下编译SOEM(Simle Open EtherCAT Master)_soem vs_CoderIsArt的博客-CSDN博客make_libsoem_lib.bat "C:\Program Files (x86)\Microsoft Visual Studio\2017\Community\VC\Auxiliary\Build" x86用QT创建…...

论文投稿指南——中文核心期刊推荐(科学、科学研究)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...
、attr()和data())
jQuery属性操作prop()、attr()和data()
jQuery 提供了一些属性操作的方法,主要包括 prop()、attr() 和 data() 等。通过这些方法,能够实现不同的需求。下面我们分别进行详细讲解。 1.prop() 方法 prop0 方法用来设置或获取元素固有属性值。元素固有属性是指元素本身自带的属性,如 …...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
