Vue如何请求接口——axios请求
1、安装axios
在cmd或powershell打开文件后,输入下面的命令
npm install axios
可在项目框架中的package.json中查看是否:
二、引用axios
import axios from 'axios'在需要使用的页面中引用
三、get方式使用
get请求使用params传参,本文只列举常用参数
axios({url: "", // urlparams: {// 参数name: xxx,age: xxx,},}).then(function (res) {console.log(res); // 成功回调}).catch(function (err) {console.log(err); // 失败回调});
四、post请求
post请求使用data传参,需要使用qs处理参数
五、qs配置
qs是axios的一个数据序列化工具,可通过npm install qs命令进行安装.然后在需要使用的页面引用
引入方法:
import axios from 'axios'
import qs from 'qs'
方法 qs.parse()、qs.stringify()
qs.stringify()将对象序列化成URL的形式,以&进行拼接
qs.parse()将URL解析成对象的形式
写法:
axios({method: "post", //请求方式url: "", //urldata: qs.stringify({// 参数}),}).then(function (res) {console.log(res); //成功回调}).catch(function (err) {console.log(err); //失败回调});
相关文章:

Vue如何请求接口——axios请求
1、安装axios 在cmd或powershell打开文件后,输入下面的命令 npm install axios 可在项目框架中的package.json中查看是否: 二、引用axios import axios from axios 在需要使用的页面中引用 三、get方式使用 get请求使用params传参,本文只列举常用参数…...
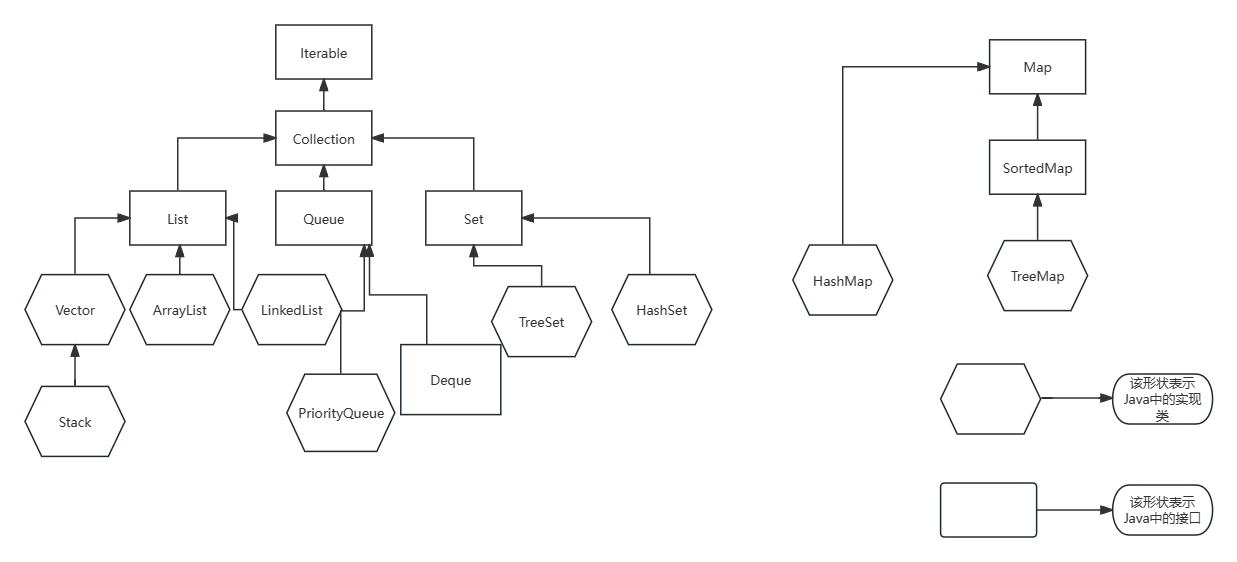
【数据结构一】初始Java集合框架(前置知识)
Java中的数据结构 Java语言在设计之初有一个非常重要的理念便是:write once,run anywhere!所以Java中的数据结构是已经被设计者封装好的了,我们只需要实例化出想使用的对象,便可以操作相应的数据结构了,本篇…...

直接将第三方数据插入到 Redis 中
Redis 是一个内存数据库,可以用于缓存和持久化数据。虽然常见的使用场景是将数据从关系型数据库(如MySQL)同步到 Redis 中进行缓存,但也可以直接将第三方数据插入到 Redis 中。 你可以通过编程语言的 Redis 客户端库(…...

【重点】【DP】322.零钱兑换
题目 法1:动态规划 // 时间复杂度:O(kN) class Solution {public int coinChange(int[] coins, int amount) {int[] dp new int[amount 1];Arrays.fill(dp, amount 1);dp[0] 0;for (int i 1; i < dp.length; i) {for (int coin : coins) {if (…...

Python入门学习篇(六)——for循环while循环
1 for循环 1.1 常规for循环 1.1.1 语法结构 for 变量名 in 可迭代对象:# 遍历对象时执行的代码 else:# 当for循环全部正常运行完(没有报错和执行break)后执行的代码1.1.2 示例代码 print("----->学生检查系统<------") student_lists["张三",&qu…...
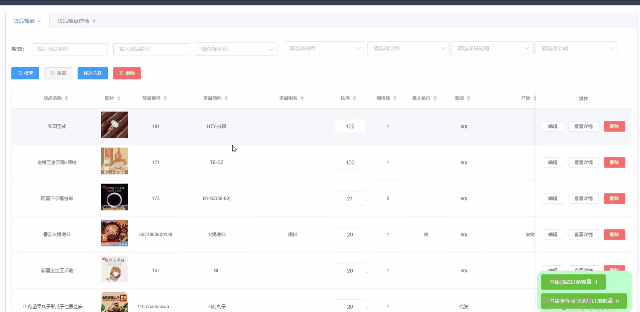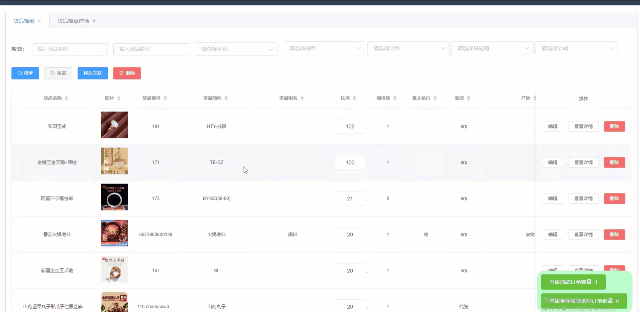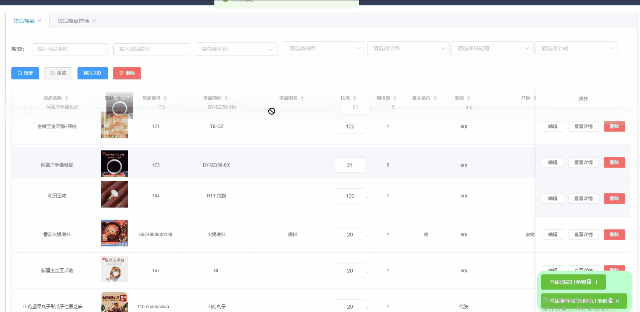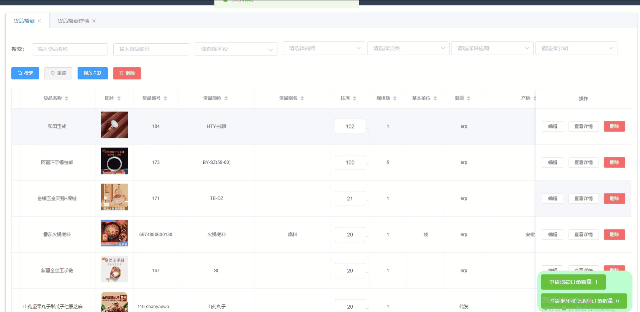
el-table 实现行拖拽排序
element ui 表格实现拖拽排序的功能,可以借助第三方插件Sortablejs来实现。 引入sortablejs npm install sortablejs --save组件中使用 import Sortable from sortablejs;<el-table ref"el-table":data"listData" row-key"id" …...
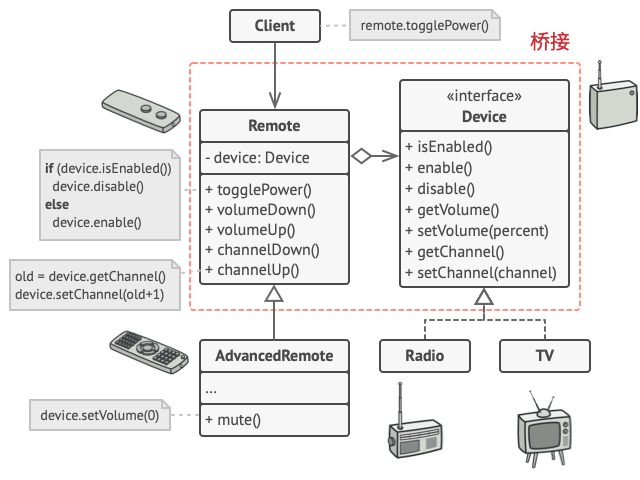
2. 结构型模式 - 桥接模式
亦称: Bridge 意图 桥接模式是一种结构型设计模式, 可将一个大类或一系列紧密相关的类拆分为抽象和实现两个独立的层次结构, 从而能在开发时分别使用 问题 抽象? 实现? 听上去挺吓人? 让我们慢慢来&#x…...

最小二乘法简介
最小二乘法简介 1、背景描述2、最小二乘法2.1、最小二乘准则2.2、最小二乘法 3、最小二乘法与线性回归3.1、最小二乘法与线性回归3.2、最小二乘法与最大似然估计 4、正态分布(高斯分布) 1、背景描述 在工程应用中,我们通常会用一组观测数据去…...

mathtype公式章节编号
1. word每章标题后插入章节符 如果插入后显示章节符,需要进行隐藏 开始->样式->MTEquationSection->修改样式->字体,勾选隐藏 2. 设置mathtype公式编号格式 插入编号->格式化->设置格式...
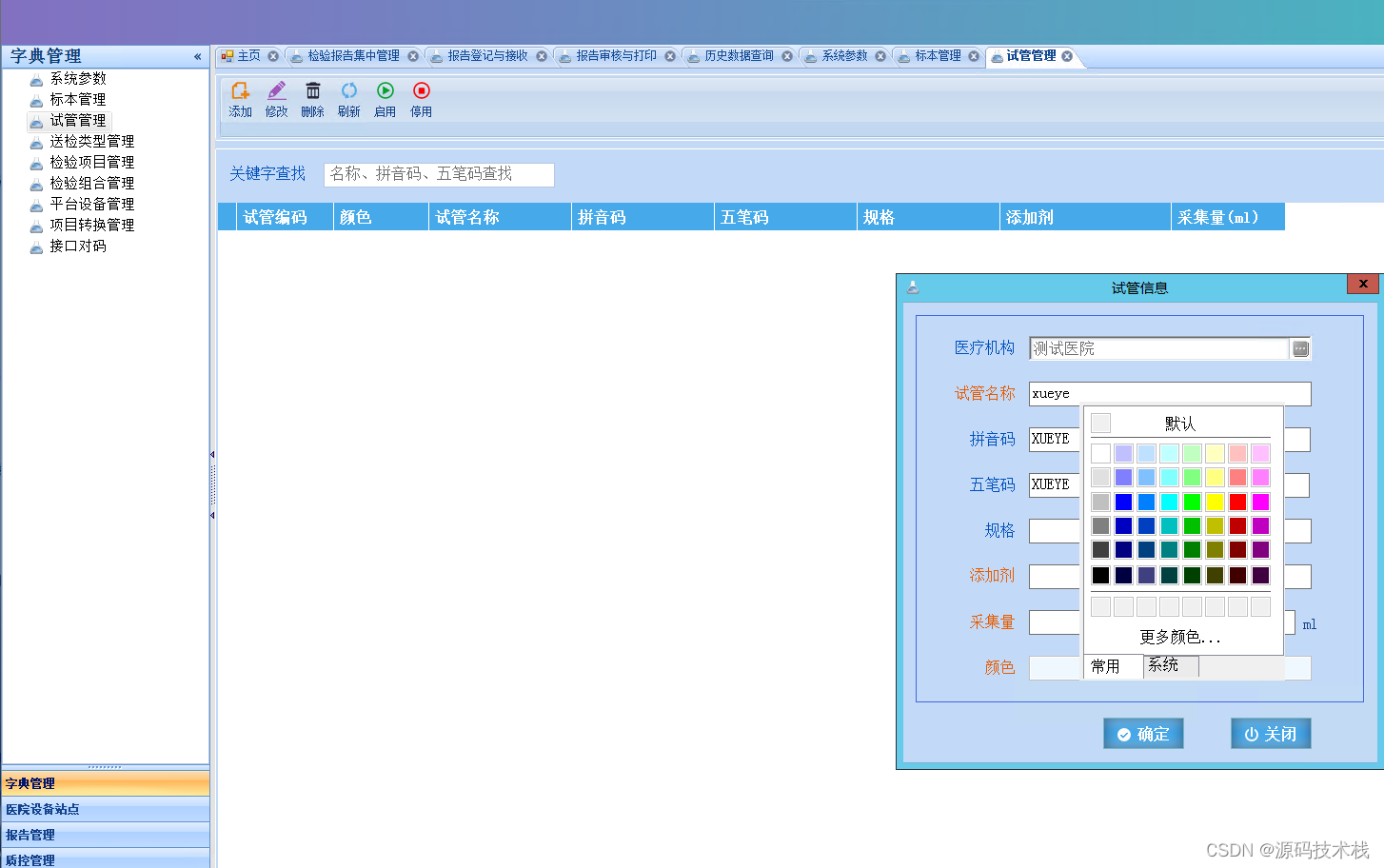
医学实验室检验科LIS信息系统源码
实验室信息管理是专为医院检验科设计的一套实验室信息管理系统,能将实验仪器与计算机组成网络,使病人样品登录、实验数据存取、报告审核、打印分发,实验数据统计分析等繁杂的操作过程实现了智能化、自动化和规范化管理。 实验室管理系统功能介…...
无需改动现有网络,企业高速远程访问内网Linux服务器
某企业为数据治理工具盒厂商,帮助客户摆脱数据问题困扰、轻松使用数据,使得客户可以把更多精力投入至数据应用及业务赋能,让数据充分发挥其作为生产要素的作用。 目前,该企业在北京、南京、西安、武汉等地均设有产研中心ÿ…...
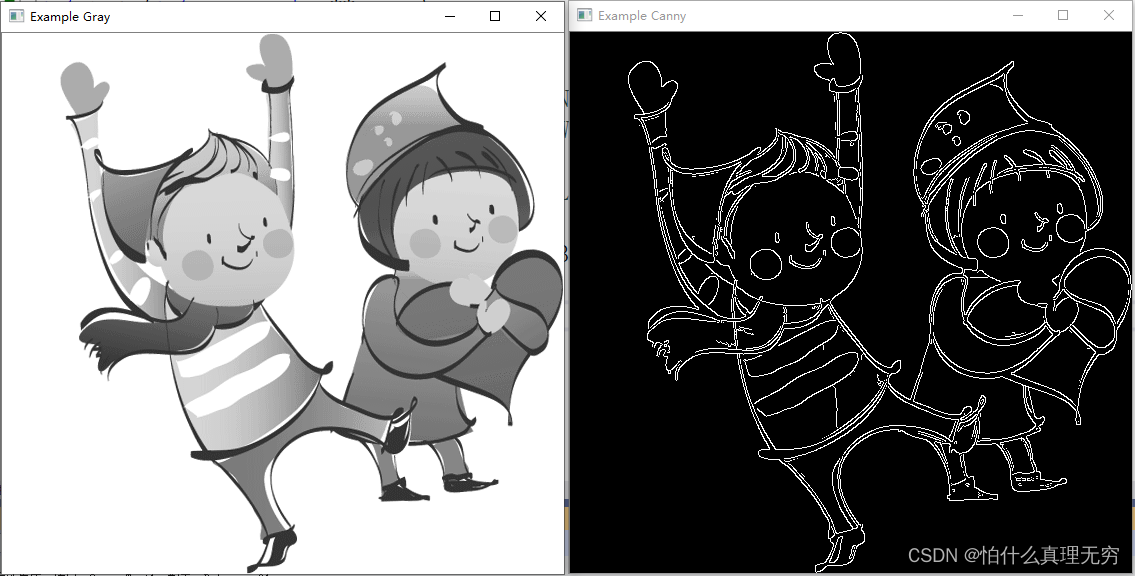
Opencv入门五 (显示图片灰度值)
源码如下: #include <opencv2/opencv.hpp> int main(int argc, char** argv) { cv::Mat img_rgb, img_gry, img_cny; cv::namedWindow("Example Gray",cv::WINDOW_AUTOSIZE); cv::namedWindow("Example Canny", cv::WINDOW_…...
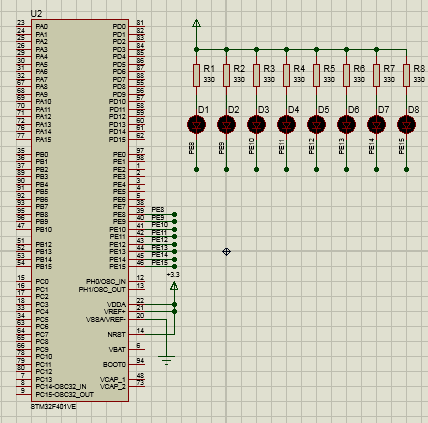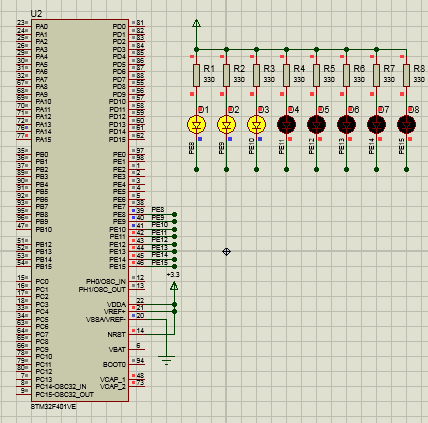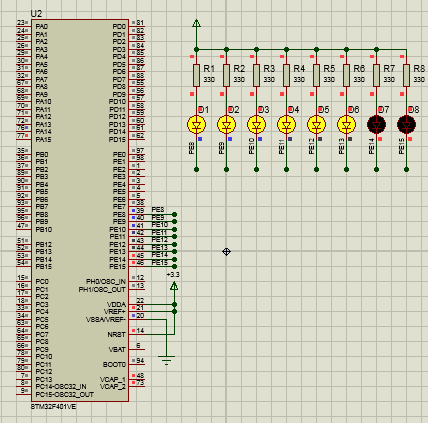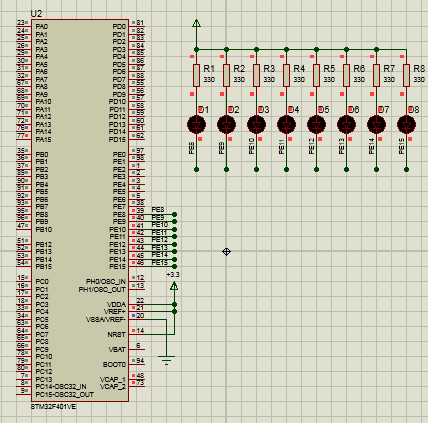
STM32F4 HAL流水灯Proteus仿真
源码下载:https://download.csdn.net/download/zlkk00/88654405...
【K8s】4# 使用kuboard部署开源项目实战
文章目录 1.开源项目2.实战2.1.创建spring-blade命名空间2.2.导入 spring-blade 到 K8S 名称空间2.3.设置存储卷参数2.4.调整节点端口2.5.确认导入2.6.查看集群2.7.导入配置到 nacos2.8.启动微服务工作负载 3.验证部署结果3.1.Nacos3.2. web 4.问题汇总Q1:Nacos启动…...

Mysql数据库(1)
目录 一.操作系统 二.数据库mysql 对象: 库 -> 表 -> 二维表格形式的结构化数据 常用的数据类型: MySQL的六大约束属性: SQL语句 :DDL DML DQL DCL 三.mysql的基础操作 查看当前服务器中的数据库 查看当前服务器中…...

网络安全-API接口安全
本文为作者学习文章,按作者习惯写成,如有错误或需要追加内容请留言(不喜勿喷) 本文为追加文章,后期慢慢追加 API接口概念 API接口(Application Programming Interface,应用程序编程接口&…...

flutter学习-day16-自定义组件
📚 目录 介绍组合多个组件自绘组件 Custompaint绘制边界RepaintBoundaryCustomPainter与Canvas画笔Paint绘制组件例子 本文学习和引用自《Flutter实战第二版》:作者:杜文 1. 介绍 当Flutter提供的现有组件无法满足我们的需求,或…...

XML简介 (EXtensible Markup Language)
XML简介 (EXtensible Markup Language) 可扩展标记语言 特点 XML与操作系统、编程语言的开发平台无关实现不同系统之间的数据交换 作用 数据交互配置应用程序和网站Ajax基石 XML标签 XML文档内容由一系列标签元素组成 <元素名 属性名"属性值">元素内容&l…...

基于Spring自动注入快速实现策略模式+工厂模式优化过多的if..else
一、策略模式 1.1策略模式定义 在策略模式(Strategy Pattern)中一个类的行为或其算法可以在运行时更改。这种类型的设计模式属于行为型模式。 在策略模式定义了一系列算法或策略,并将每个算法封装在独立的类中,使得它们可以互相…...
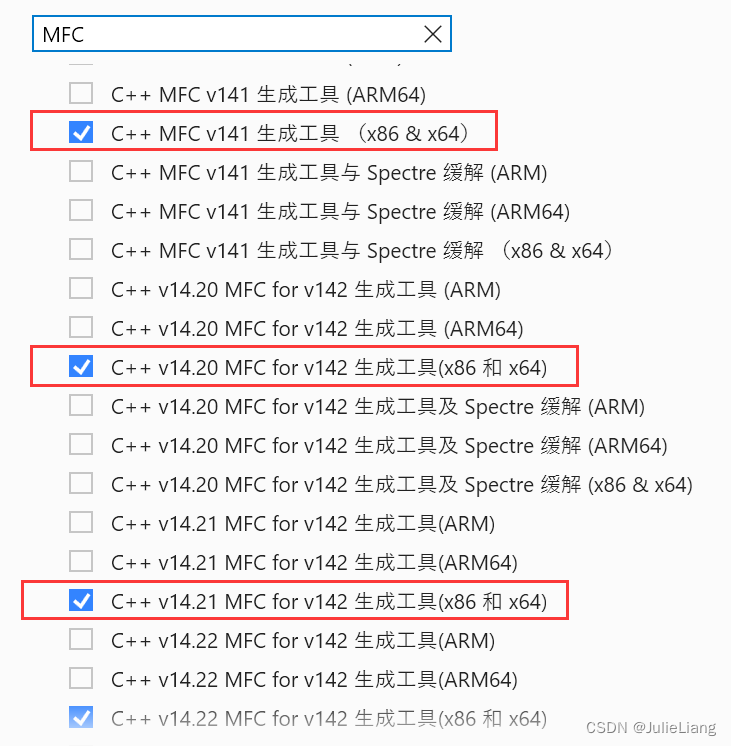
安装vcpkg管理opencv的安装+MFC缺失的解决
第一步,出现#include没有办法找到opencv头文件的问题,无法解决 在VC的提示下,安装了vcpkg,然后用vcpkg命令来帮助安装opencv,过程十分顺利。 1. cmd 到命令行窗口; 2. 建立src文件夹,并进入…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
