最小二乘法简介
最小二乘法简介
- 1、背景描述
- 2、最小二乘法
- 2.1、最小二乘准则
- 2.2、最小二乘法
- 3、最小二乘法与线性回归
- 3.1、最小二乘法与线性回归
- 3.2、最小二乘法与最大似然估计
- 4、正态分布(高斯分布)
1、背景描述
在工程应用中,我们通常会用一组观测数据去估计模型的参数,模型是我们根据经验知识预先给定的。例如,我们有一组观测数据 ( x i , y i ) (x_i,y_i) (xi,yi),通过简单分析,我们猜测y与x之间存在线性关系,那么我们的模型可以给定为:
y = k x + b y=kx+b y=kx+b
该模型只有两个参数,理论上,我们只需要通过两组观测值建立二元一次方程组即可求解。类似的,如果模型有n个参数,我们只需要n组观测值即可求解。换句话说,这种情况下,模型的参数是唯一确定解
但是,在实际应用中,由于我们的观测会存在误差(偶然误差、系统误差等),所以我们总会做更多观测。例如,在上述例子中,尽管只有两个参数,但是我们可能会观测n组数据: ( x 0 , y 0 ) 、 ( x 1 , y 1 ) 、 . . . 、 ( x n − 1 , y n − 1 ) (x_0,y_0)、(x_1,y_1)、...、(x_{n-1},y_{n-1}) (x0,y0)、(x1,y1)、...、(xn−1,yn−1),这会导致我们无法找到一条直线经过所有的点,也就是说,方程无确定解

于是,这就是我们要解决的问题:虽然没有确定解,但是我们能不能求出近似解,使得模型能在各个观测点上达到“最佳“拟合
那么“最佳”的准则是什么?可以是所有观测点到直线的距离和最小,也可以是所有观测点到直线预测点(真实值-理论值)的绝对值和最小,还可以是所有观测点到直线预测点(真实值-理论值)的平方和最小

2、最小二乘法
2.1、最小二乘准则
19世纪初(1806年),法国科学家勒让德发明了“最小二乘法”。勒让德认为,让误差(真实值-理论值)的平方和最小估计出来的模型是最接近真实情形的。换句话说,勒让德认为最佳的拟合准则是使 y i y_i yi与 y = f ( x i ) y=f(x_i) y=f(xi)的距离的平方和最小:
L = ∑ i = 1 m ( y i − f ( x i ) ) 2 L=\sum_{i=1}^m(y_i-f(x_i))^2 L=i=1∑m(yi−f(xi))2
这个准则也被称为最小二乘准则。这个目标函数取得最小值时的函数参数,就是最小二乘法的思想,所谓“二乘”就是平方的意思
勒让德在原文中提到:使误差平方和达到最小,在各方程的误差之间建立了一种平衡,从而防止了某一极端误差取得支配地位,而这有助于揭示系统的更接近真实的状态
至于为什么最佳准则就是误差平方而不是其它的,勒让德当时并没有给出解释,直到后来高斯建立了正态误差分析理论才成功回答了该问题

1829年,高斯建立了一套误差分析理论,从而证明了确实是使误差(真实值-理论值)平方和最小的情况下系统是最优的
误差分析理论其实说到底就一个结论:观察值的误差服从标准正态分布,即 ϵ ∈ N ( 0 , 1 ) ϵ∈N(0,1) ϵ∈N(0,1)
关于正态分布的介绍见本文第4节
2.2、最小二乘法
最小二乘法就是一个数学公式,在数学上称为曲线拟合,不仅包括线性回归方程,还包括矩阵的最小二乘法
最小二乘法是解决曲线拟合问题最常用的方法。令

其中, φ k ( x ) \varphi_k(x) φk(x)是事先选定的一组线性无关的函数, a k a_k ak是待定系数 ( k = 1 , 2 , . . . , m , m < n ) (k=1,2,...,m,m<n) (k=1,2,...,m,m<n),拟合准则是使 y i ( i = 1 , 2 , . . . , n ) y_i(i=1,2,...,n) yi(i=1,2,...,n)与 f ( x i ) f(x_i) f(xi)的距离 δ i \delta_i δi的平方和最小,称为最小二乘准则
百度百科词条给出的基本原理如下:

最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和最小
最小二乘法是一种在误差估计、不确定度、系统辨识及预测、预报等数据处理诸多学科领域得到广泛应用的数学工具
3、最小二乘法与线性回归
3.1、最小二乘法与线性回归
对于勒让德给定的最佳拟合准则,我们可以看到,最小二乘法其实就是用来做函数拟合的一种思想。至于如何求解具体的参数那就是另外一个问题了
最小二乘法的本质是一种数学思想,它可以拟合任意函数。而线性回归只是其中一个比较简单且常用的函数,所以讲最小二乘法基本都会以线性回归为例
线性回归因为比较简单,可以直接推导出解析解,而且许多非线性的问题也可以转化为线性问题来解决,所以得到了广泛的应用
线性回归简介见文章:传送门
3.2、最小二乘法与最大似然估计
最大似然估计:最大化给定样本集发生的概率,即就是极大化似然函数(Likelihood Function),而似然函数就是样本的联合概率。由于我们通常都会假设样本是相互独立的,因此联合概率就等于每个样本发生的概率乘积
假设我们有m组观测数据 ( x 1 , y 1 ) , . . . , ( x m , y m ) (x_1,y_1),...,(x_m,y_m) (x1,y1),...,(xm,ym),我们猜测其关系符合:
y = k x + b y=kx+b y=kx+b
假设真实值与预测值之间的误差为:
ε i = y i − y = y i − f ( x i ) \varepsilon_i=y_i-y=y_i-f(x_i) εi=yi−y=yi−f(xi)
根据高斯的误差分析理论,观测值的误差服从标准正态分布(见文末),即给定一个 x i x_i xi,模型输出真实值 y i y_i yi的概率为:
p ( y i ∣ x i ) = 1 2 π e − ε i 2 2 p(y_i|x_i)=\frac{1}{\sqrt{2\pi}}e^{-\frac{\varepsilon_i^2}{2}} p(yi∣xi)=2π1e−2εi2
则根据最大似然估计(似然函数)有:
L ( ω ) = ∏ i = 1 m p ( y i ∣ x i ) = ∏ i = 1 m 1 2 π e − ε i 2 2 L(\omega)=\prod_{i=1}^mp(y_i|x_i)=\prod_{i=1}^m\frac{1}{\sqrt{2\pi}}e^{-\frac{\varepsilon_i^2}{2}} L(ω)=i=1∏mp(yi∣xi)=i=1∏m2π1e−2εi2
两边取对数得:
J ( ω ) = l n ( L ( ω ) ) = ∑ i = 1 m l n ( 1 2 π e − ε i 2 2 ) = ∑ i = 1 m l n 1 2 π − 1 2 ∑ i = 1 m ε i 2 J(\omega)=ln(L(\omega)) = \sum_{i=1}^mln(\frac{1}{\sqrt{2\pi}}e^{-\frac{\varepsilon_i^2}{2}}) = \sum_{i=1}^mln\frac{1}{\sqrt{2\pi}}-\frac{1}{2}\sum_{i=1}^m\varepsilon_i^2 J(ω)=ln(L(ω))=i=1∑mln(2π1e−2εi2)=i=1∑mln2π1−21i=1∑mεi2
去掉无关常数项得:
J ( ω ) = l n ( L ( ω ) ) = − 1 2 ∑ i = 1 m ε i 2 = − 1 2 ∑ i = 1 m ( y i − f ( x i ) ) 2 J(\omega)=ln(L(\omega))=-\frac{1}{2}\sum_{i=1}^m\varepsilon_i^2=-\frac{1}{2}\sum_{i=1}^m(y_i-f(x_i))^2 J(ω)=ln(L(ω))=−21i=1∑mεi2=−21i=1∑m(yi−f(xi))2
要使 L ( ω ) L(\omega) L(ω)(概率)最大,即 J ( ω ) J(\omega) J(ω)最大,则使下面多项式结果最小即可:
∑ i = 1 m ( y i − f ( x i ) ) 2 \sum_{i=1}^m(y_i-f(x_i))^2 i=1∑m(yi−f(xi))2
上述结果表明:最大似然估计(似然函数)等价于最小二乘法,这也表明了以误差平方和作为最佳拟合准则的合理性
因此我们可以说,最小二乘法其实就是误差满足正态(高斯)分布的极大似然估计,最小化误差平方本质上等同于在误差服从正态(高斯)分布的假设下的最大似然估计
4、正态分布(高斯分布)
正态分布(Normal Distribution),也称高斯分布(Gaussian Distribution),其曲线呈钟型,两头低,中间高,左右对称,因此也被称为钟形曲线
定义:若连续型随机变量x有如下形式的密度函数:

则称x服从参数为 ( μ , σ 2 ) (\mu,\sigma^2) (μ,σ2)的正态分布(Normal Distribution),记为 X − N ( μ , σ 2 ) X-N(\mu,\sigma^2) X−N(μ,σ2)

性质:
- 关于 x = μ x=μ x=μ 对称,在 x = μ x=μ x=μ 处达到最大值 1 2 π σ \frac{1}{\sqrt{2\pi}\sigma} 2πσ1,越远离 μ μ μ,密度函数值越小
- 数学期望(均值)为 μ μ μ,标准差为 σ \sigma σ,方差为 σ 2 \sigma^2 σ2
标准正态分布:又称 μ μ μ分布,是以0为均值(数学期望)、以1为标准差的正态分布,记为 X − N ( 0 , 1 ) X-N(0,1) X−N(0,1),密度函数:

参考文章:
https://blog.csdn.net/MoreAction_/article/details/106443383
https://blog.csdn.net/MoreAction_/article/details/121591653
https://blog.csdn.net/qq_46092061/article/details/119136137
相关文章:

最小二乘法简介
最小二乘法简介 1、背景描述2、最小二乘法2.1、最小二乘准则2.2、最小二乘法 3、最小二乘法与线性回归3.1、最小二乘法与线性回归3.2、最小二乘法与最大似然估计 4、正态分布(高斯分布) 1、背景描述 在工程应用中,我们通常会用一组观测数据去…...

mathtype公式章节编号
1. word每章标题后插入章节符 如果插入后显示章节符,需要进行隐藏 开始->样式->MTEquationSection->修改样式->字体,勾选隐藏 2. 设置mathtype公式编号格式 插入编号->格式化->设置格式...
医学实验室检验科LIS信息系统源码
实验室信息管理是专为医院检验科设计的一套实验室信息管理系统,能将实验仪器与计算机组成网络,使病人样品登录、实验数据存取、报告审核、打印分发,实验数据统计分析等繁杂的操作过程实现了智能化、自动化和规范化管理。 实验室管理系统功能介…...
无需改动现有网络,企业高速远程访问内网Linux服务器
某企业为数据治理工具盒厂商,帮助客户摆脱数据问题困扰、轻松使用数据,使得客户可以把更多精力投入至数据应用及业务赋能,让数据充分发挥其作为生产要素的作用。 目前,该企业在北京、南京、西安、武汉等地均设有产研中心ÿ…...
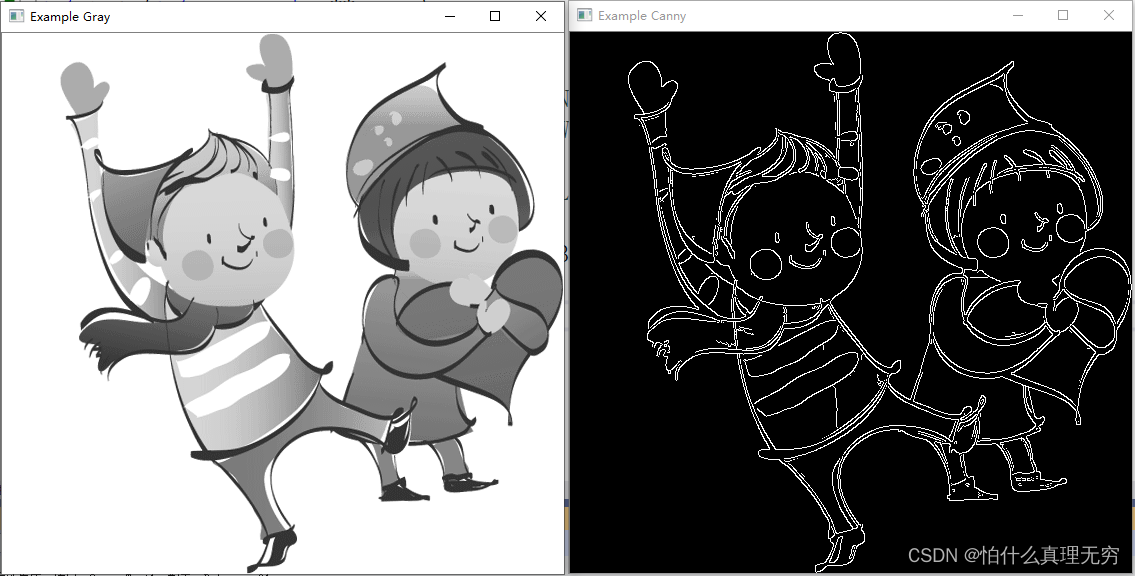
Opencv入门五 (显示图片灰度值)
源码如下: #include <opencv2/opencv.hpp> int main(int argc, char** argv) { cv::Mat img_rgb, img_gry, img_cny; cv::namedWindow("Example Gray",cv::WINDOW_AUTOSIZE); cv::namedWindow("Example Canny", cv::WINDOW_…...
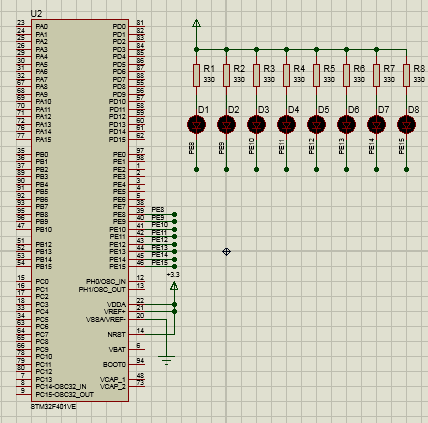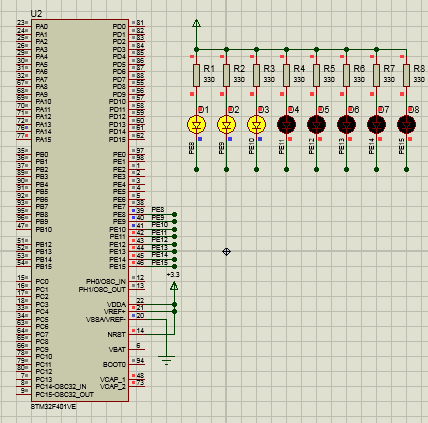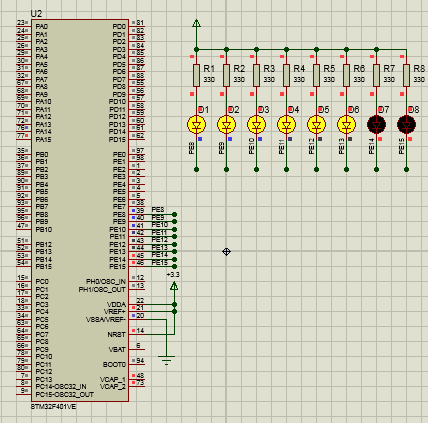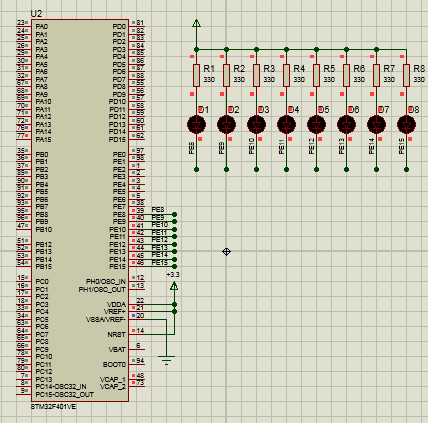
STM32F4 HAL流水灯Proteus仿真
源码下载:https://download.csdn.net/download/zlkk00/88654405...
【K8s】4# 使用kuboard部署开源项目实战
文章目录 1.开源项目2.实战2.1.创建spring-blade命名空间2.2.导入 spring-blade 到 K8S 名称空间2.3.设置存储卷参数2.4.调整节点端口2.5.确认导入2.6.查看集群2.7.导入配置到 nacos2.8.启动微服务工作负载 3.验证部署结果3.1.Nacos3.2. web 4.问题汇总Q1:Nacos启动…...

Mysql数据库(1)
目录 一.操作系统 二.数据库mysql 对象: 库 -> 表 -> 二维表格形式的结构化数据 常用的数据类型: MySQL的六大约束属性: SQL语句 :DDL DML DQL DCL 三.mysql的基础操作 查看当前服务器中的数据库 查看当前服务器中…...

网络安全-API接口安全
本文为作者学习文章,按作者习惯写成,如有错误或需要追加内容请留言(不喜勿喷) 本文为追加文章,后期慢慢追加 API接口概念 API接口(Application Programming Interface,应用程序编程接口&…...

flutter学习-day16-自定义组件
📚 目录 介绍组合多个组件自绘组件 Custompaint绘制边界RepaintBoundaryCustomPainter与Canvas画笔Paint绘制组件例子 本文学习和引用自《Flutter实战第二版》:作者:杜文 1. 介绍 当Flutter提供的现有组件无法满足我们的需求,或…...

XML简介 (EXtensible Markup Language)
XML简介 (EXtensible Markup Language) 可扩展标记语言 特点 XML与操作系统、编程语言的开发平台无关实现不同系统之间的数据交换 作用 数据交互配置应用程序和网站Ajax基石 XML标签 XML文档内容由一系列标签元素组成 <元素名 属性名"属性值">元素内容&l…...

基于Spring自动注入快速实现策略模式+工厂模式优化过多的if..else
一、策略模式 1.1策略模式定义 在策略模式(Strategy Pattern)中一个类的行为或其算法可以在运行时更改。这种类型的设计模式属于行为型模式。 在策略模式定义了一系列算法或策略,并将每个算法封装在独立的类中,使得它们可以互相…...
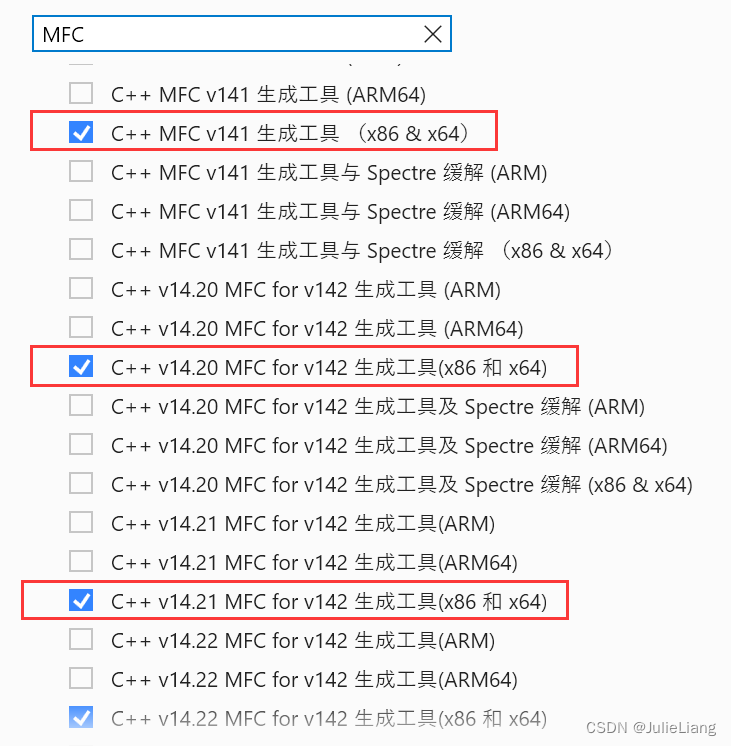
安装vcpkg管理opencv的安装+MFC缺失的解决
第一步,出现#include没有办法找到opencv头文件的问题,无法解决 在VC的提示下,安装了vcpkg,然后用vcpkg命令来帮助安装opencv,过程十分顺利。 1. cmd 到命令行窗口; 2. 建立src文件夹,并进入…...

了解树和学习二叉树
1.树 1.1 概念 树是一种 非线性 的数据结构,它是由 n ( n>0 )个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看 起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 。 注意:树形结构中…...

Spring Boot学习随笔- 拦截器实现和配置(HandlerInterceptor、addInterceptors)、jar包部署和war包部署
学习视频:【编程不良人】2021年SpringBoot最新最全教程 第十三章、拦截器 拦截器 :Interceptor 拦截 中断 类似于javaweb中的Filter,不过没有Filter那么强大 作用 Spring MVC的拦截器是一种用于在请求处理过程中进行预处理和后处理的机制。拦…...
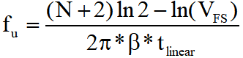
Pipelined-ADC设计二——结构指标及非理想因素(Part2)
接上文,本章将两个比较重要的非理想因素,因此各项指标制定。后续会对常见的非理想因素给出常见的解决方法,以及设计所采用的方法。 2.2.7. 比较器失调 在流水线 ADC 中,比较器的主要误差来源就是比较器失调,称为失调误…...
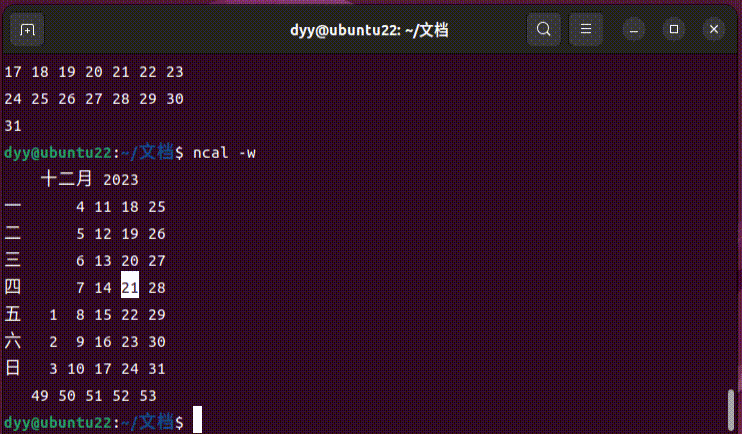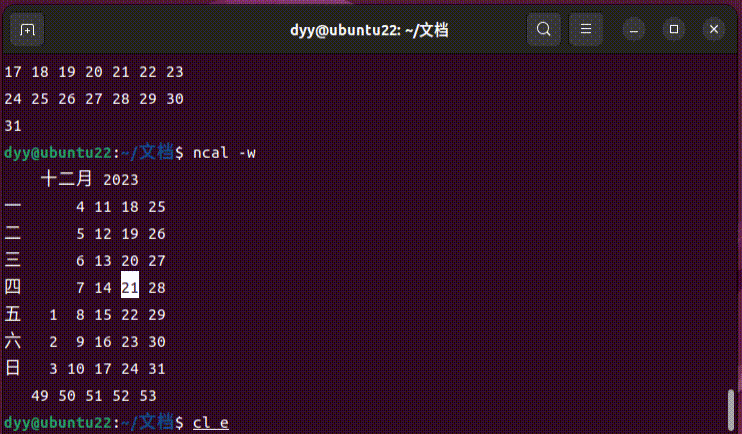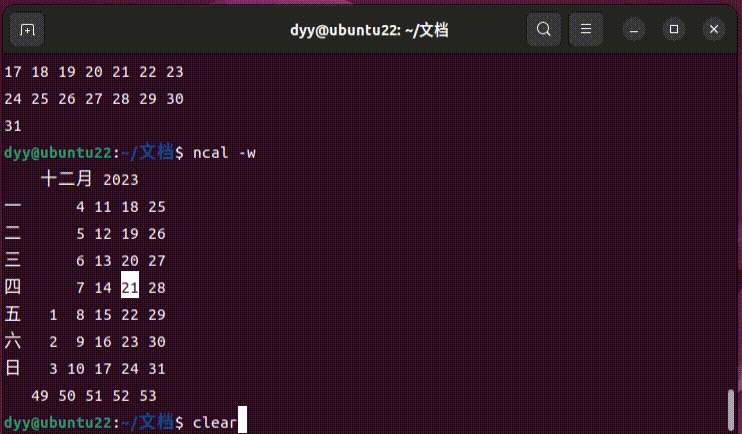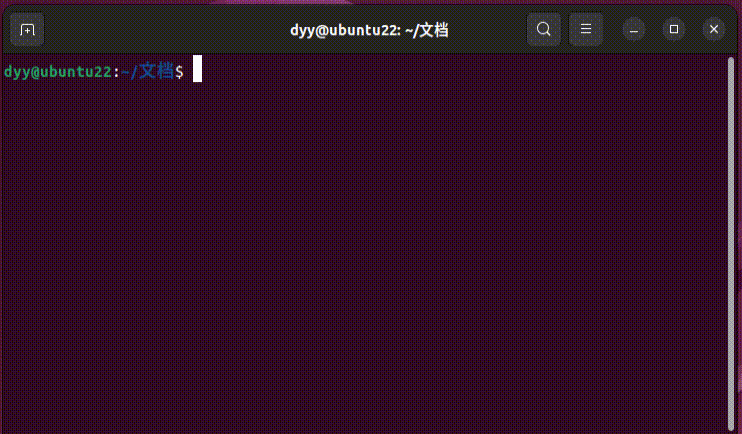
Ubuntu 常用命令之 clear 命令用法介绍
📑Linux/Ubuntu 常用命令归类整理 clear命令在Ubuntu系统下用于清除终端屏幕的内容。这个命令没有任何参数,它的主要作用就是清理终端屏幕上的所有信息,使得屏幕看起来像是新打开的一样。 使用clear命令非常简单,只需要在终端中…...

【JAVA面试题】什么是对象锁?什么是类锁?
🍎 个人博客 :个 人 主 页 🏆个人专栏:多线程JAVA ⛳️ 功 不 唐 捐 ,玉 汝 于 成 目录 前言 回答 对象锁(Object Lock): 类锁(Class Lock)࿱…...

飞天使-k8s知识点5-kubernetes基础名词扫盲
文章目录 deploymentspodNodeserviceskubectl 实现应用伸缩kubectl 实现滚动更新kubernetes架构 deployments 中文文档 http://docs.kubernetes.org.cn/251.htmldeployment是用来创建和更新应用的,master 会负责将创建好的应用实例调度到集群中的各个节点 应用实例…...

【视觉实践】使用Mediapipe进行目标检测:杯子检测和椅子检测实践
目录 1 Mediapipe 2 Solutions 3 安装mediapipe 4 实践 1 Mediapipe Mediapipe是google的一个开源项目,可以提供开源的、跨平台的常用机器学习(machine learning,ML)方案。MediaPipe是一个用于构建机器学习管道</...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
