了解树和学习二叉树

1.树
1.1 概念

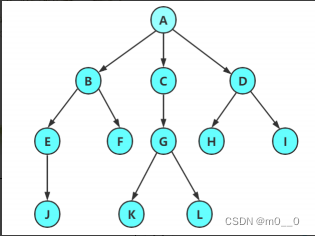
注意:树形结构中,子树之间不能有交集,否则就不是树形结构 !!!
一颗N结点的树有N-1条边

2. 二叉树(重点)
2.1 概念

二叉树的每个节点的度 <= 2
2.2 两种特殊的二叉树
满二叉树:每层的结点数都达到最大值,就是满二叉树。(每个节点的度=2)
完全二叉树:有n 个结点的二叉树,从上到下,从左到右,编号从0至n-1的结点一 一对应时称之为完 全二叉树。
满二叉树是一种特殊的完全二叉树。

2.3 二叉树的性质
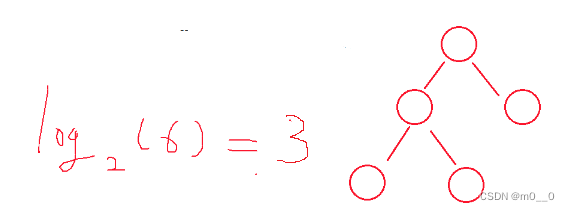
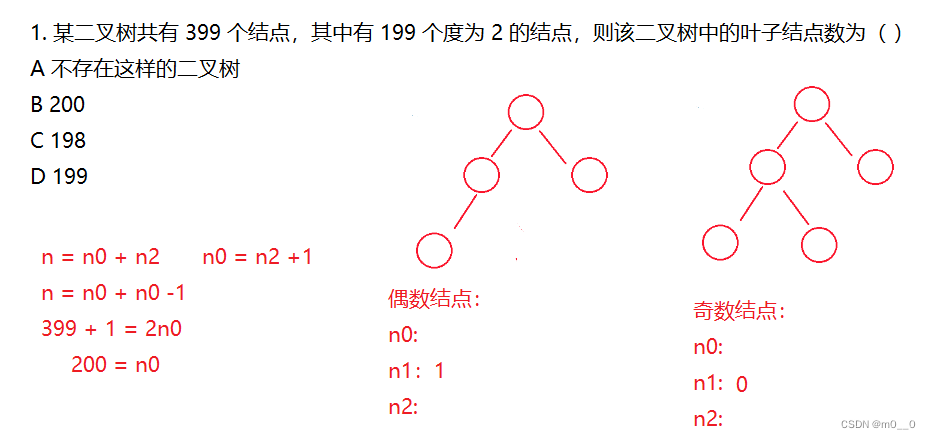
2.4 二叉树的遍历



前序遍历和后序遍历是无法构成一棵树的!
无法确定左、右子树
相关文章:

了解树和学习二叉树
1.树 1.1 概念 树是一种 非线性 的数据结构,它是由 n ( n>0 )个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看 起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 。 注意:树形结构中…...

Spring Boot学习随笔- 拦截器实现和配置(HandlerInterceptor、addInterceptors)、jar包部署和war包部署
学习视频:【编程不良人】2021年SpringBoot最新最全教程 第十三章、拦截器 拦截器 :Interceptor 拦截 中断 类似于javaweb中的Filter,不过没有Filter那么强大 作用 Spring MVC的拦截器是一种用于在请求处理过程中进行预处理和后处理的机制。拦…...
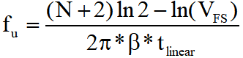
Pipelined-ADC设计二——结构指标及非理想因素(Part2)
接上文,本章将两个比较重要的非理想因素,因此各项指标制定。后续会对常见的非理想因素给出常见的解决方法,以及设计所采用的方法。 2.2.7. 比较器失调 在流水线 ADC 中,比较器的主要误差来源就是比较器失调,称为失调误…...
Ubuntu 常用命令之 clear 命令用法介绍
📑Linux/Ubuntu 常用命令归类整理 clear命令在Ubuntu系统下用于清除终端屏幕的内容。这个命令没有任何参数,它的主要作用就是清理终端屏幕上的所有信息,使得屏幕看起来像是新打开的一样。 使用clear命令非常简单,只需要在终端中…...

【JAVA面试题】什么是对象锁?什么是类锁?
🍎 个人博客 :个 人 主 页 🏆个人专栏:多线程JAVA ⛳️ 功 不 唐 捐 ,玉 汝 于 成 目录 前言 回答 对象锁(Object Lock): 类锁(Class Lock)࿱…...

飞天使-k8s知识点5-kubernetes基础名词扫盲
文章目录 deploymentspodNodeserviceskubectl 实现应用伸缩kubectl 实现滚动更新kubernetes架构 deployments 中文文档 http://docs.kubernetes.org.cn/251.htmldeployment是用来创建和更新应用的,master 会负责将创建好的应用实例调度到集群中的各个节点 应用实例…...

【视觉实践】使用Mediapipe进行目标检测:杯子检测和椅子检测实践
目录 1 Mediapipe 2 Solutions 3 安装mediapipe 4 实践 1 Mediapipe Mediapipe是google的一个开源项目,可以提供开源的、跨平台的常用机器学习(machine learning,ML)方案。MediaPipe是一个用于构建机器学习管道</...

C++之深拷贝进阶
目录 拷贝构造函数的深拷贝进阶版本 赋值运算符重载的深拷贝进阶 总结 上期我们学习了C中深拷贝的传统版本,今天我们将学习更为高效的版本。 拷贝构造函数的深拷贝进阶版本 传统版本代码如下: string(string& s):_str(new char[strlen(s._str)…...

导行电磁波从纵向场分量求其他方向分量的矩阵表示
导行电磁波从纵向场分量求解其他方向分量的矩阵表示 导行电磁波传播的特点 电磁波在均匀、线性、各向同性的空间中沿着 z z z轴传播,可用分离变量法将时间轴、 z z z轴与 x , y x,y x,y轴分离,电磁波的形式可表示为: E ⃗ E ⃗ ( x , y )…...

融资项目——swagger2的注解
1. ApiModel与ApiModelProperty(在实体类中使用) 如上图,ApiModel加在实体类上方,用于整体描述实体类。ApiModelProperty(value"xxx",example"xxx")放于每个属性上方,用于对属性进行描述。swagger2网页上的效果如下图&am…...

【性能优化】MySql数据库查询优化方案
阅读本文你的收获 了解系统运行效率提升的整体解决思路和方向学会MySQl中进行数据库查询优化的步骤学会看慢查询、执行计划、进行性能分析、调优 一、问题:如果你的系统运行很慢,你有什么解决方案? 关于这个问题,我们通常首先…...
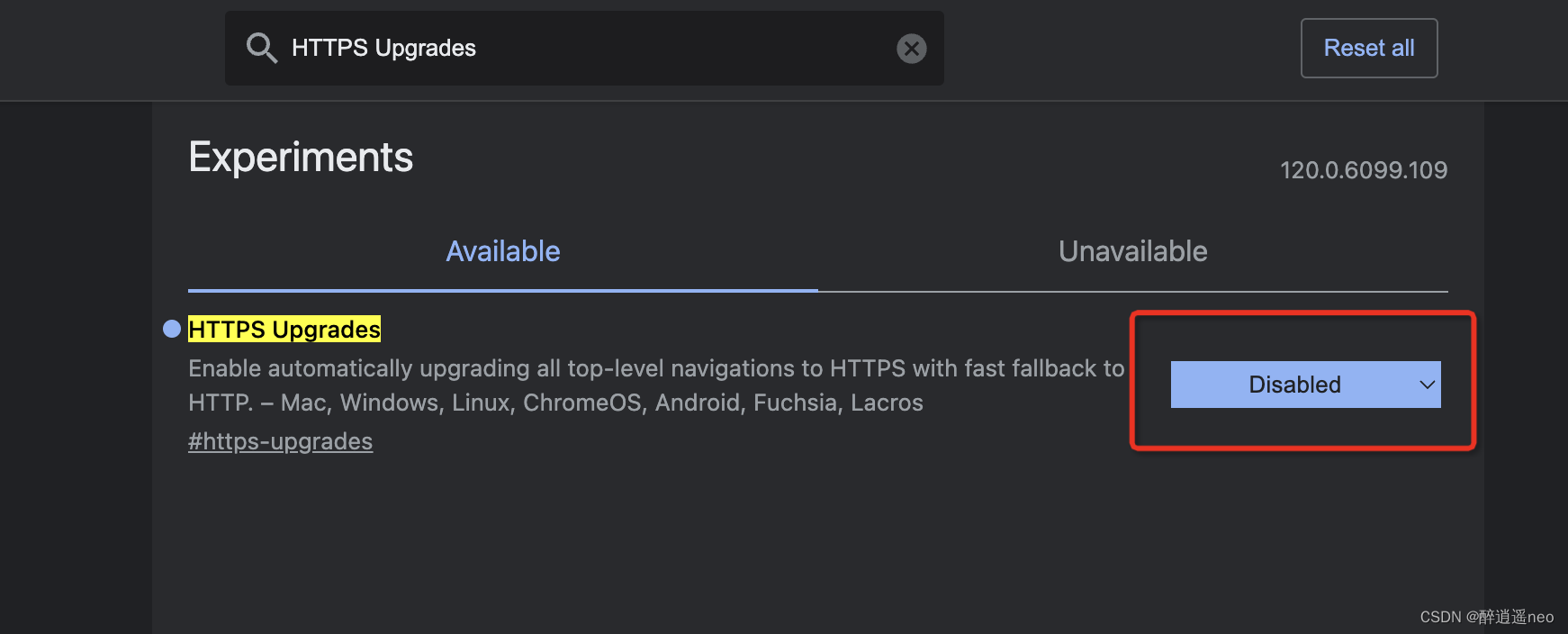
Chrome浏览器http自动跳https问题
现象: Chrome浏览器访问http页面时有时会自动跳转https,导致一些问题。比如: 开发阶段访问dev环境网址跳https,后端还是http,导致接口跨域。 复现: 先访问http网址,再改成https访问…...

【C++进阶02】多态
一、多态的概念及定义 1.1 多态的概念 多态简单来说就是多种形态 同一个行为,不同对象去完成时 会产生出不同的状态 多态分为静态多态和动态多态 静态多态指的是编译时 在程序编译期间确定了程序的行为 比如:函数重载 动态多态指的是运行时 在程序运行…...
PHP开发日志——循环和条件语句嵌套不同,效率不同(循环内加入条件语句,条件语句判断后加入循环,array_map函数中加入条件语句)
十多年前开发框架时,为了效率不断试过各种代码写法,今天又遇到了,想想php8时代会不会有所变化,结果其实也还是和当年一样,但当年没写博客,但现在可以把数据记录下来了。 PHP_loop_ireflies_dark_forest 项目…...
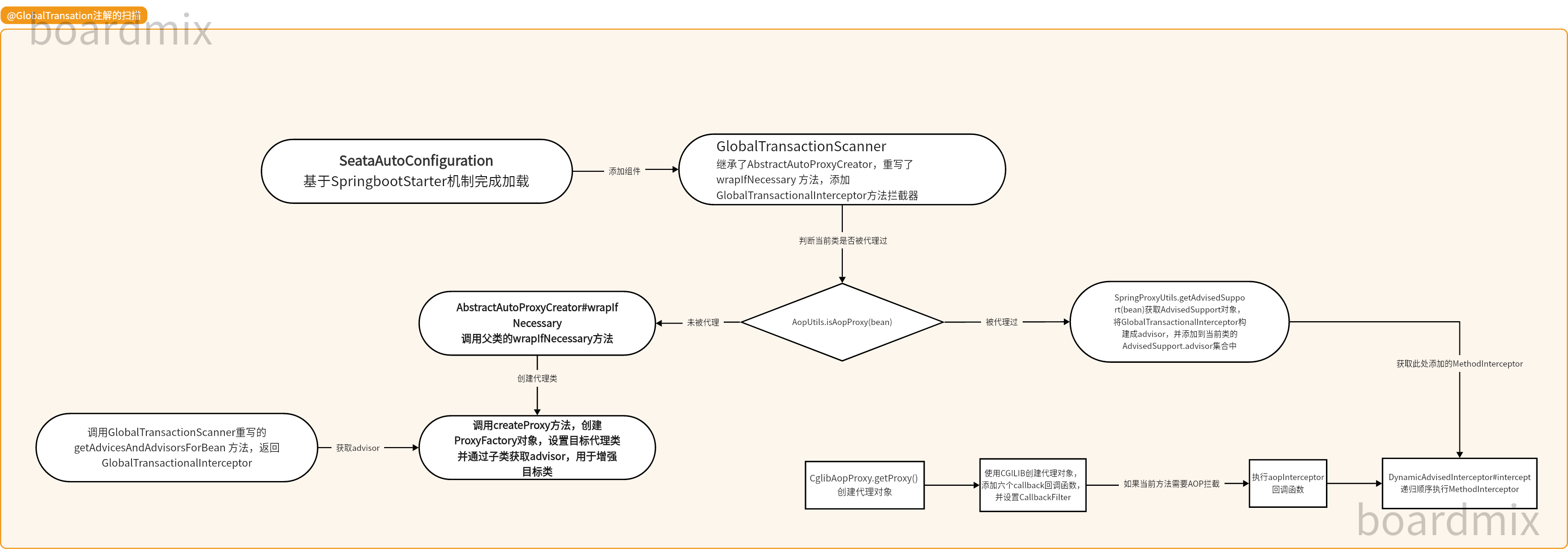
【Seata源码学习 】 扫描@GlobalTransaction注解 篇一
1. SeataAutoConfiguration 自动配置类的加载 基于SpringBoot的starter机制,在应用上下文启动时,会加载SeataAutoConfiguration自动配置类 # Auto Configure org.springframework.boot.autoconfigure.EnableAutoConfigurationio.seata.spring.boot.aut…...
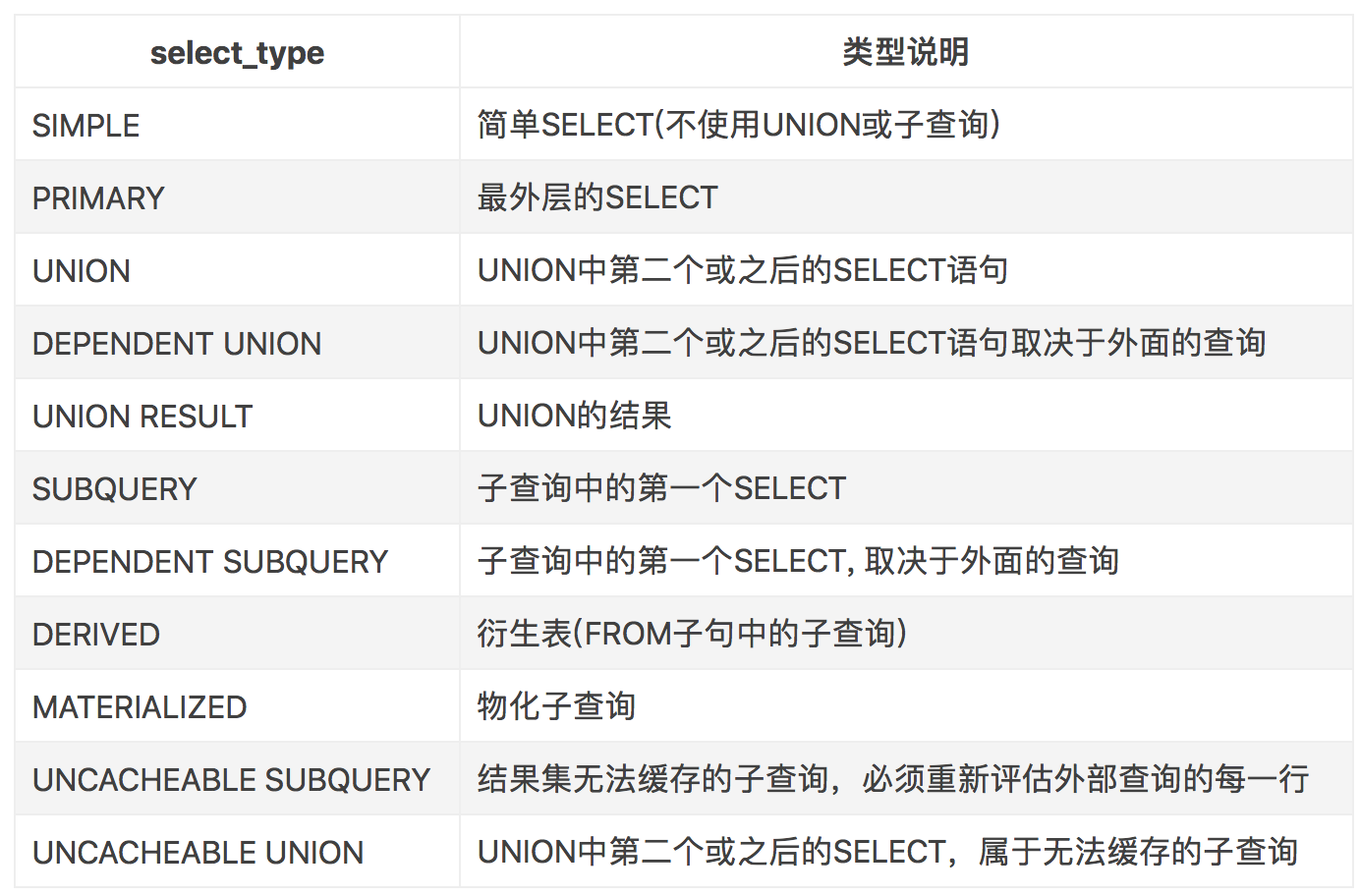
DBA-MySql面试问题及答案-上
文章目录 1.什么是数据库?2.如何查看某个操作的语法?3.MySql的存储引擎有哪些?4.常用的2种存储引擎?6.可以针对表设置引擎吗?如何设置?6.选择合适的存储引擎?7.选择合适的数据类型8.char & varchar9.Mysql字符集10.如何选择…...
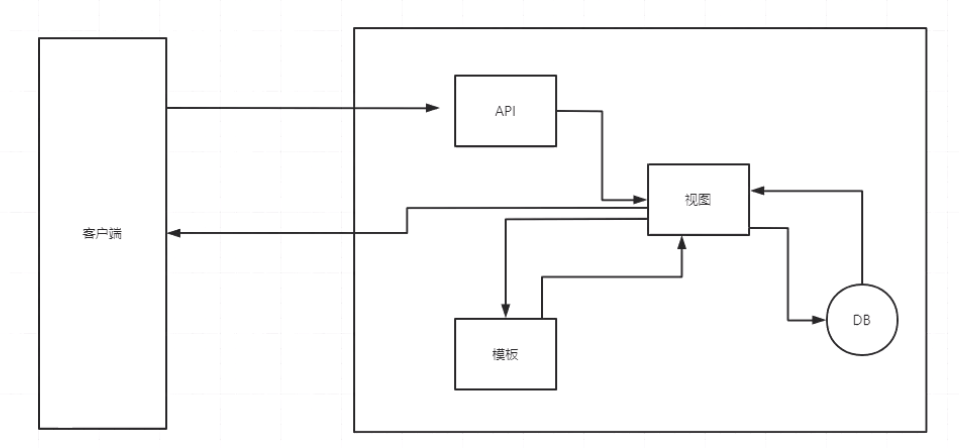
网络爬虫之Ajax动态数据采集
动态数据采集 规则 有时候我们在用 requests 抓取页面的时候,得到的结果可能和在浏览器中看到的不一样,在浏览器中可以看到正常显示的页面教据,但是使用 requests 得到的结果并没有,这是因为requests 获取的都是原始的 HTML 文档…...

c语言的初始学习(练习)
##初学c语言---MOOC浙江大学翁恺先生学习c语言 那么我们先看看这个题目吧,这是初始语法的应用。 记住,我们的程序是按步骤执行的,并不是在不同的两行同时进行。 程序设计:1.了解题目的需要,几个变量需要用到&#x…...

研究论文 2022-Oncoimmunology:AI+癌RNA-seq数据 识别细胞景观
Wang, Xin, et al. "Deep learning using bulk RNA-seq data expands cell landscape identification in tumor microenvironment." Oncoimmunology 11.1 (2022): 2043662. https://www.tandfonline.com/doi/full/10.1080/2162402X.2022.2043662 被引次数࿱…...

ChatGPT4与ArcGIS Pro3助力AI 地理空间分析和可视化及助力科研论文写作
在地学领域,ArcGIS几乎成为了每位科研工作者作图、数据分析的必备工具,而ArcGIS Pro3除了良好地继承了ArcMap强大的数据管理、制图、空间分析等能力,还具有二三维融合、大数据、矢量切片制作及发布、任务工作流、时空立方体等特色功能&#x…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
