解决 MATLAB 遗传算法中 exitflg=4 的问题
一、优化问题简介
以求解下述优化问题为例:
P 1 : min p ∑ k = 1 K p k s . t . { ∑ k = 1 K R k r e q l o g ( 1 + α k ∗ p k ) ≤ B b s , ∀ k ∈ K p k ≥ 0 , ∀ k ∈ K \begin{align} {P_1:}&\mathop{\min}_{\bm{p}}{ \sum\limits_{k=1}^K p_k } \nonumber \\ &s.t. \begin{cases} \sum\limits_{k=1}^K \frac{R_k^{req}}{log(1+\alpha_k * p_k) } \leq B^{bs}, \forall k \in \mathcal{K} \nonumber \\ p_k \geq 0, \forall k \in \mathcal{K} \end{cases} \end{align} P1:minpk=1∑Kpks.t.⎩ ⎨ ⎧k=1∑Klog(1+αk∗pk)Rkreq≤Bbs,∀k∈Kpk≥0,∀k∈K
其中, p k p_k pk是决策变量, α k \alpha_k αk、 R k r e q R_k^{req} Rkreq、 B b s B^{bs} Bbs均是已知的正常数, K = { 1 , 2 , … , K } \mathcal{K}=\{1,2,\dots,K\} K={1,2,…,K}表示变量的索引数。
二、有问题的代码
先以 K = 2 K=2 K=2 为例,调用遗传算法,编写下述代码,以求解上述优化问题:
1. 主函数:
clear all
clc
para.K = 2 ;para.alpha = ones( para.K , 1 );
para.B_bs = 10 ;
para.R_req = [ 3.6702 ; 5.2690 ] ; % 2*rand( para.K , 1 ) + 5 ; LB = zeros( para.K , 1 ) + 10^(-5);
[X,FVAL,EXITFLAG,OUTPUT] = ga( @(x) myfit(x,para), para.K ,[], [],[],[],LB,[], @(x) nonlcon(x,para),[] )
2. 目标函数:
function f = myfit( x , para )f = sum(x);
end
3. 非线性约束函数:
function [ g , h ] = nonlcon( x , para )
g = sum( para.R_req ./ log2( 1 + para.alpha .* x' ) ) - para.B_bs;
h=[] ;
在代码中的参数设定下,我的运行结果不稳定:(MATLAB R2014a版本)
- 运行好的结果如下(exitflg=1):
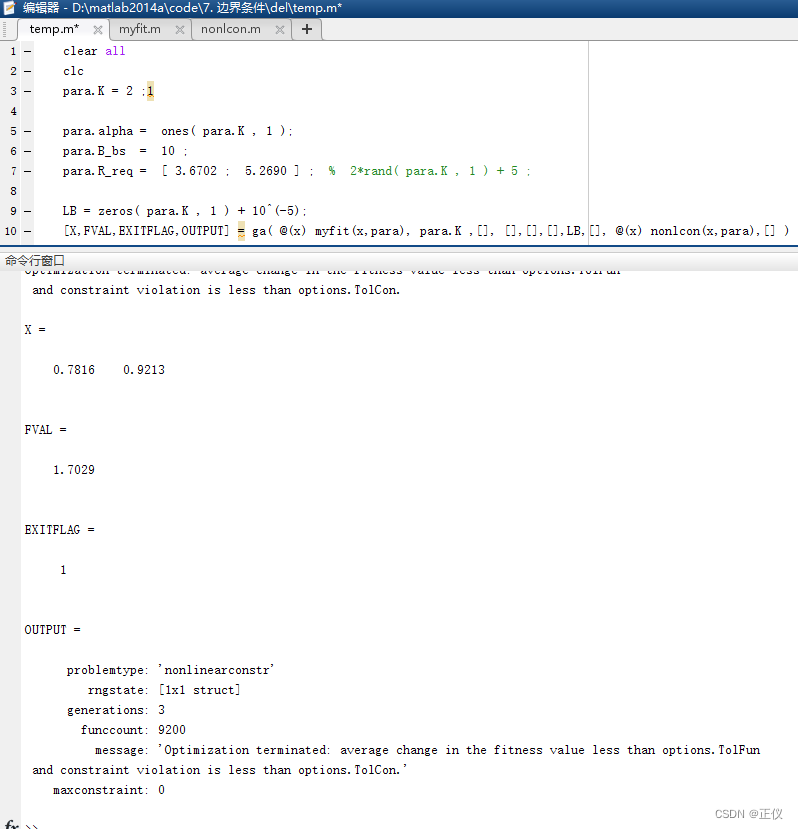
- 运行不好的结果如下(exitflg=4):
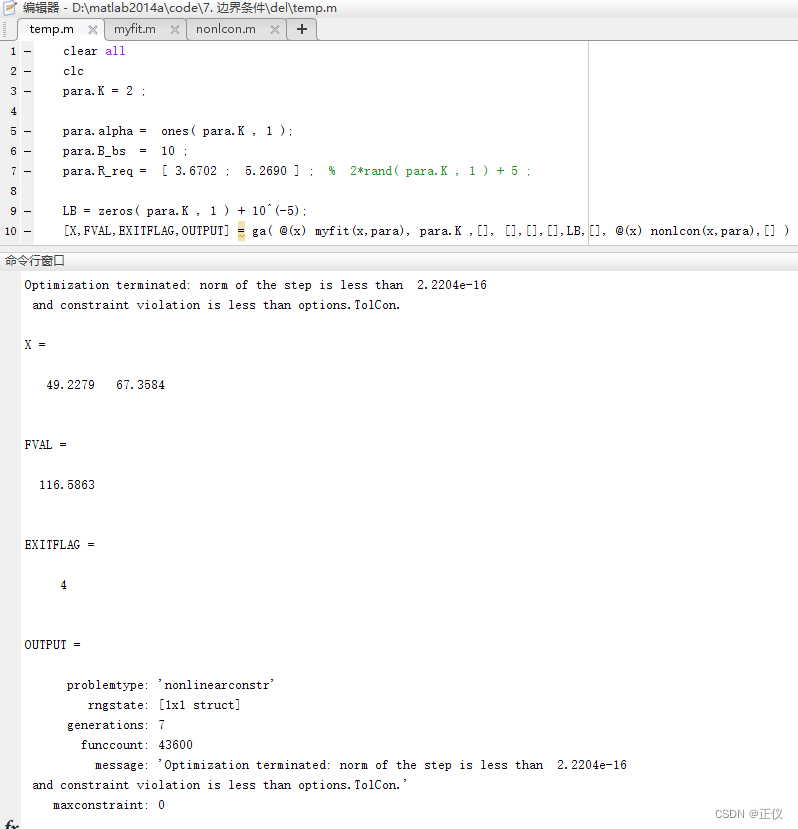
GA提示:
Optimization terminated: norm of the step is less than 2.2204e-16and constraint violation is less than options.TolCon.
GA函数返回迭代终止原因是步长范数过小,显示exitflg=4。
我搜了很多网址,寻找 exitflg=4 的原因,在以下两处资料中得到答案:
(1)官方MATLAB的文档

(2)exitFlag meaning in GA solver
“when the solution change is smaller than matlab capability (exit flag 4), this means you may need to improve your objective function.”
三、解决方案
在我的优化问题中,我将 low bound 从原始的 1 0 − 5 10^{-5} 10−5 提高到 0.1 就好了…… (由 log 函数的定义可知,决策变量 p k p_k pk 需要大于等于0,在我的问题中, p k p_k pk越远离0,越不会出现 exitflg=4 的情况,且 p k p_k pk 的最优解也没有取在0的附近,因此我可以设成了0.1)
因此,将main函数改为下式:
clear all
clc
para.K = 2 ;para.alpha = ones( para.K , 1 );
para.B_bs = 10 ;
para.R_req = [ 3.6702 ; 5.2690 ] ; % 2*rand( para.K , 1 ) + 5 ; LB = zeros( para.K , 1 ) + 0.1;
[X,FVAL,EXITFLAG,OUTPUT] = ga( @(x) myfit(x,para), para.K ,[], [],[],[],LB,[], @(x) nonlcon(x,para),[] )
此后运行结果非常稳定!

四、其他方案
在摸索 exitflg=4 的原因过程中,除了前述上调 low bound 令其远离 log 小于0的区域以外,我还发现了一些其他两个可有效缓解 exitflg=4 的方案:
- 增大种群规模(如:PopulationSize=300)
- 扩大目标函数(如:给目标函数乘以100倍)
- 增大迭代轮数(如:Generations=2000)
具体调试过程见下图:
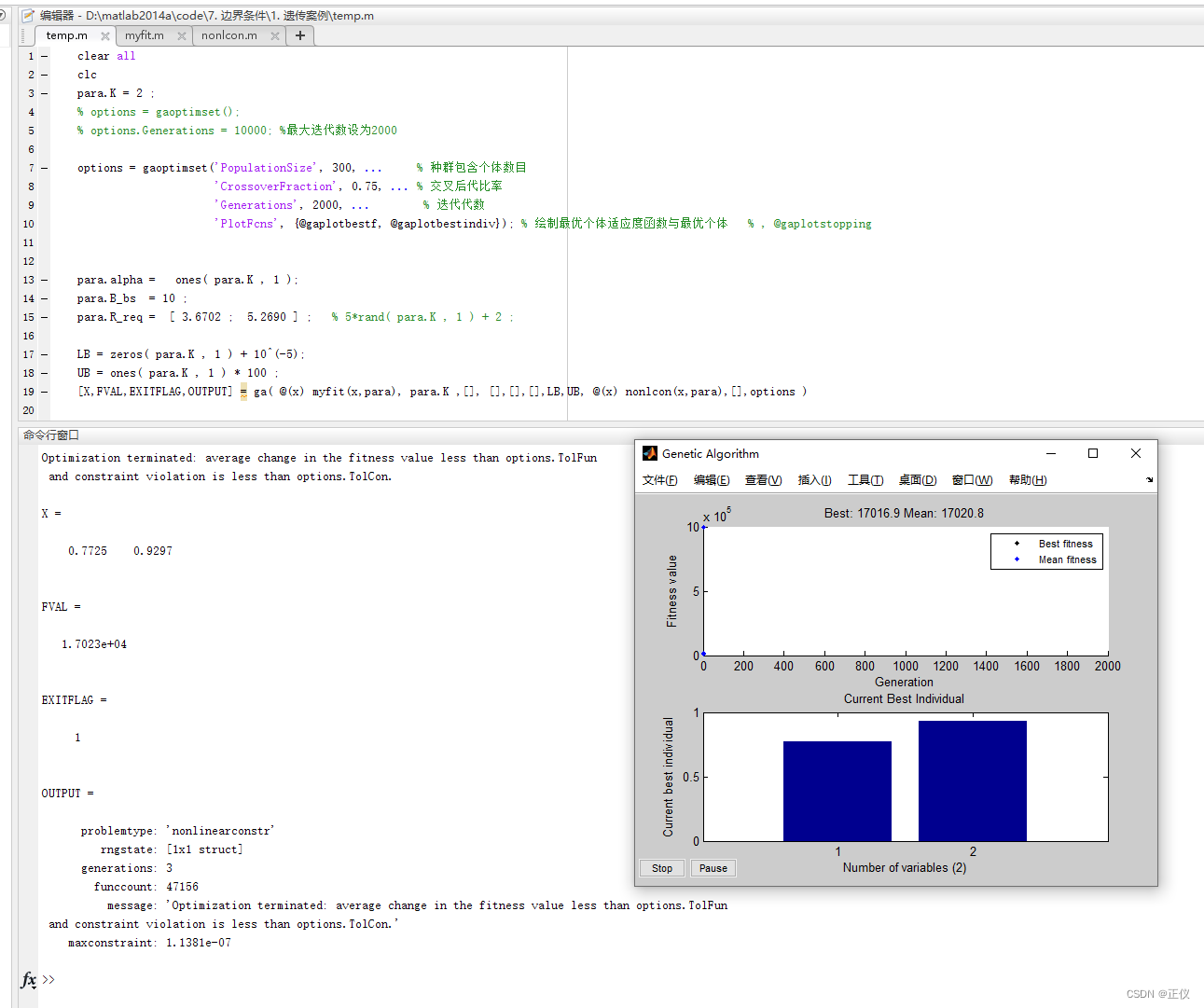
(1)目标函数扩大100倍以后:‘Generations’, 为2000、种群规模增长到300 时,exitflg仍为4,但此时已经很接近最优解了。
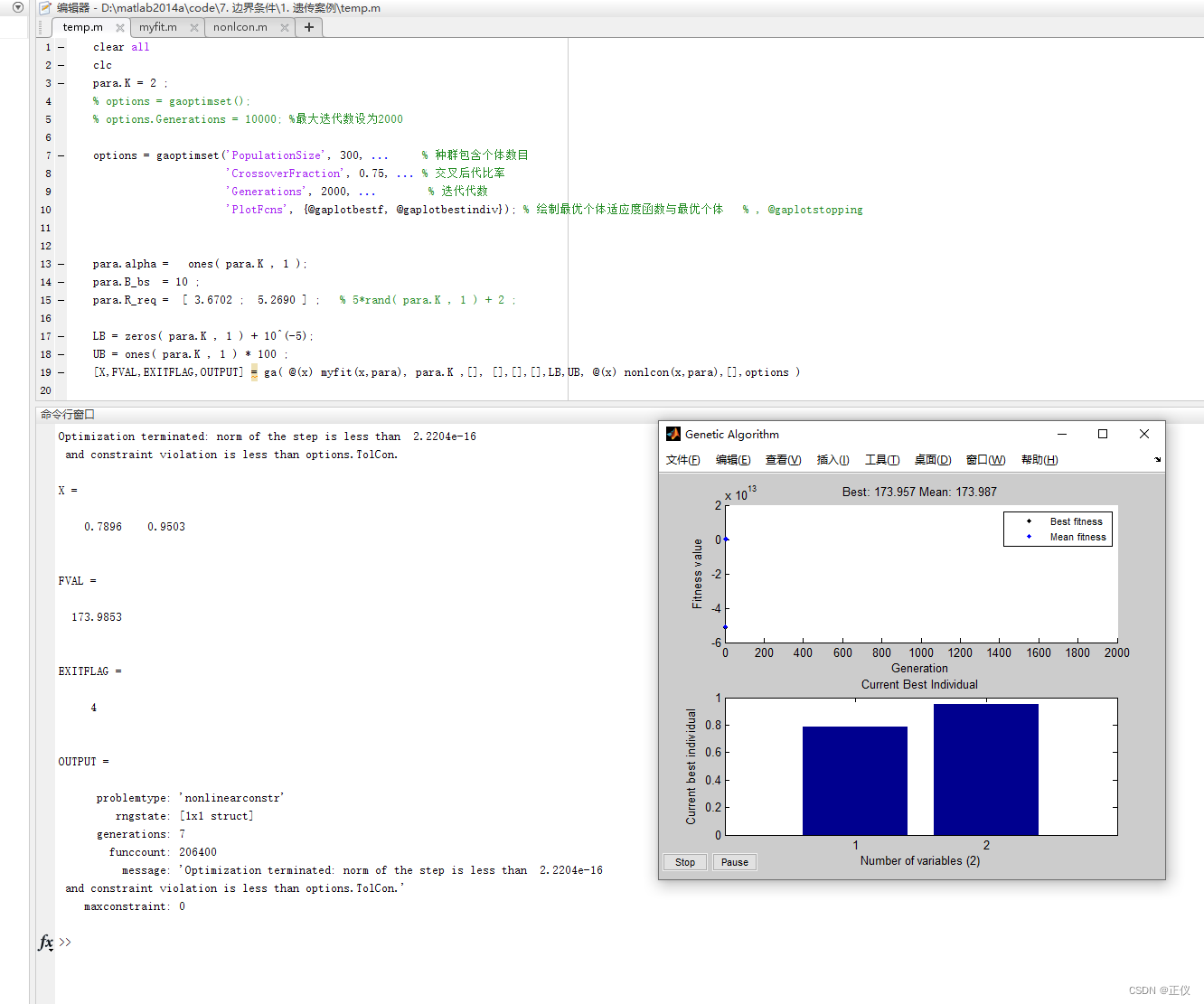
(2)目标函数扩大100倍以后:‘Generations’, 为10000、种群规模增长到300 时(即增大迭代次数),exitflg偶尔为4,大部分时间为1,此时就是最优解
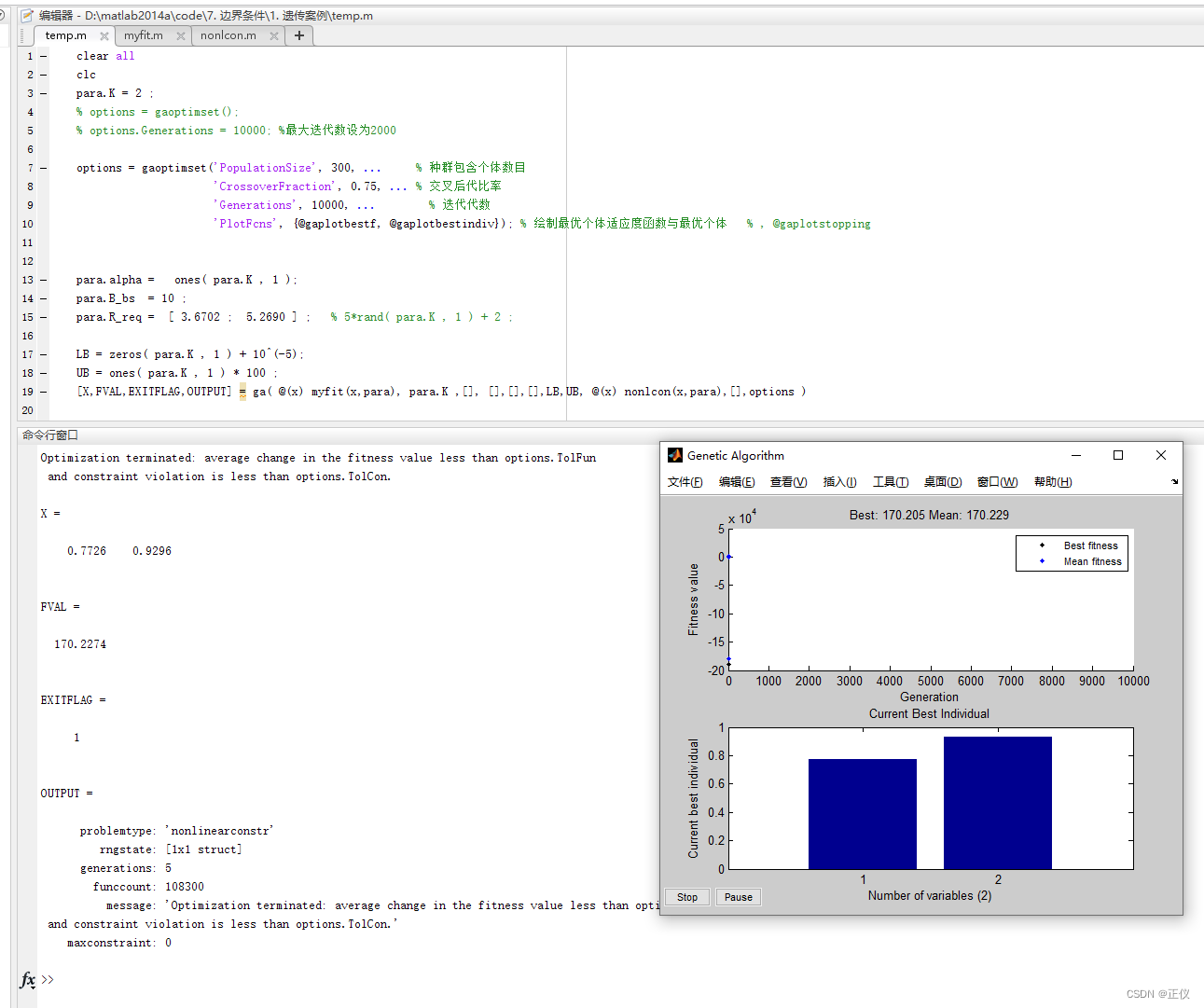
(3)目标函数扩大10000倍以后:‘Generations’, 即使为2000、种群规模为300 时,exitflg大部分情况也会为1
由此可知,增大种群规模、扩大目标函数、增大迭代轮数等方法,确实可以减缓 exitflg=4 的情况。
五、最终代码
解决了该问题后,本篇博客文末附上最终代码:
1. 主函数:
clear all
clc
para.K = 8 ;
% options = gaoptimset('PopulationSize', 100, ... % 种群包含个体数目
% 'CrossoverFraction', 0.75, ... % 交叉后代比率
% 'Generations', 2000, ... % 迭代代数
% 'TolFun',10^(-2), ...
% 'TolCon',10^(-2), ...
% 'PlotFcns', {@gaplotbestf, @gaplotbestindiv}); % 绘制最优个体适应度函数与最优个体 % , @gaplotstoppingpara.alpha = ones( para.K , 1 );
para.B_bs = 10 ;
para.R_req = 5*rand( para.K , 1 ) + 2 ; % [ 3.6702 ; 5.2690 ] ; % LB = zeros( para.K , 1 ) + 0.1;
UB = ones( para.K , 1 ) * 100 ;
[X,FVAL,EXITFLAG,OUTPUT] = ga( @(x) myfit(x,para), para.K ,[], [],[],[],LB,UB, @(x) nonlcon(x,para),[])
% [X,FVAL,EXITFLAG,OUTPUT] = ga( @(x) myfit(x,para), para.K ,[], [],[],[],LB,UB, @(x) nonlcon(x,para),[],options )
2. 目标函数:
function f = myfit( x , para )f = sum(x);
end
3. 非线性约束函数:
function [ g , h ] = nonlcon( x , para )
g = sum( para.R_req ./ log2( 1 + para.alpha .* x' ) ) - para.B_bs;
h=[] ;
运行结果:
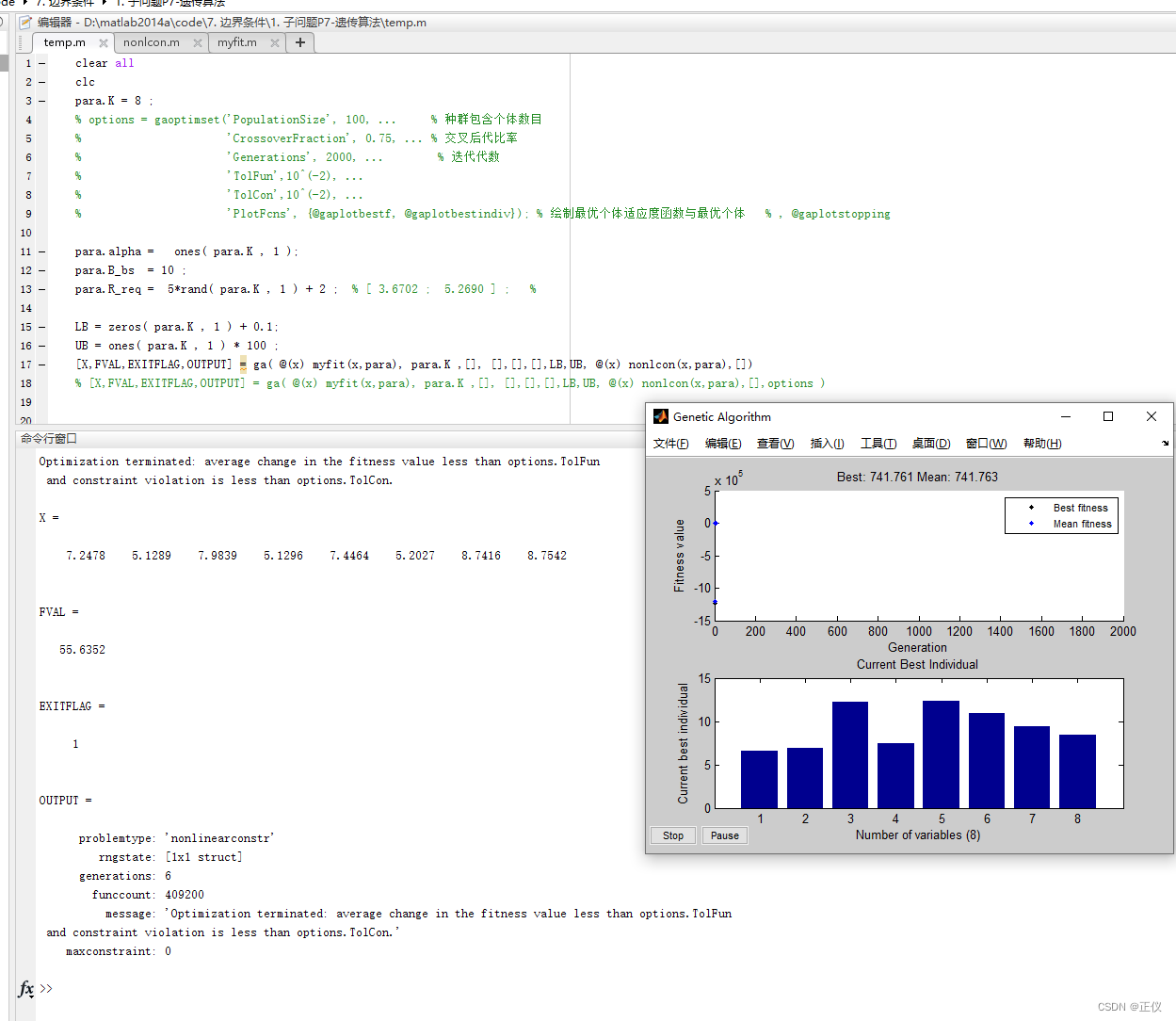
相关文章:

解决 MATLAB 遗传算法中 exitflg=4 的问题
一、优化问题简介 以求解下述优化问题为例: P 1 : min p ∑ k 1 K p k s . t . { ∑ k 1 K R k r e q l o g ( 1 α k ∗ p k ) ≤ B b s , ∀ k ∈ K p k ≥ 0 , ∀ k ∈ K \begin{align} {P_1:}&\mathop{\min}_{\bm{p}}{ \sum\limits_{k1}^K p_k } \no…...

云卷云舒:云原生业务应用成熟度模型
笔者最近学习了信通院发布的《云原生应用成熟度的评估模型》,做如下解读: 一、概述 云原生业务应用成熟度模型从企业业务应用基础设施域、应用研发域以及服务治理域等三个能力域二十个过程域综合评估企业业务应用在弹性、高可用、自愈性、可观测性以及…...

STM32的以太网外设+PHY(LAN8720)使用详解(5):MAC及DMA配置
0 工具准备 1.野火 stm32f407霸天虎开发板 2.LAN8720数据手册 3.STM32F4xx中文参考手册1 MAC及DMA配置 1.1 使能ETH时钟 stm32的ETH外设挂载在AHB1总线上,位于RCC_AHB1ENR的bit25-bit27: 相关语句如下: RCC_AHB1PeriphClockCmd(RCC_AHB1…...

GitHub、Gitee、Gitlab共用一个SSH密钥配置
目录 1. 说明2. 生成ssh2-1. 设置全局邮箱和用户名2-2. 生成全局ssh 3. Github、Gitee配置ssh3-1. Github配置3-2. Gitee配置 1. 说明 由于我的Github、Gitee、Gitlab用的邮箱不同,向不同的平台提交代码时都需要验证密码,非常麻烦所以配置了一个共用的S…...
ClickHouse集成Hive表引擎详细解析)
ClickHouse(19)ClickHouse集成Hive表引擎详细解析
文章目录 Hive集成表引擎创建表使用示例如何使用HDFS文件系统的本地缓存查询 ORC 输入格式的Hive 表在 Hive 中建表在 ClickHouse 中建表 查询 Parquest 输入格式的Hive 表在 Hive 中建表在 ClickHouse 中建表 查询文本输入格式的Hive表在Hive 中建表在 ClickHouse 中建表 资料…...

用C求斐波那契数列-----(C每日一编程)
斐波那契数列: 斐波那契数列是指这样一个数列:1,1,2,3,5,8,13,21,34,55,89……这个数列从第3项开始 ,每一项都等于前两项之和。 递推…...
在Jetpack Compose中使用ExoPlayer实现直播流和音频均衡器
在Jetpack Compose中使用ExoPlayer实现直播流和音频均衡器 背景 ExoPlayer与Media3的能力结合,为Android应用程序播放多媒体内容提供了强大的解决方案。在本教程中,我们将介绍如何设置带有Media3的ExoPlayer来支持使用M3U8 URL进行直播流。此外&#x…...

持续集成交付CICD:Jira 远程触发 Jenkins 实现更新 GitLab 分支
目录 一、实验 1.环境 2.GitLab 查看项目 3.Jira新建模块 4. Jira 通过Webhook 触发Jenkins流水线 3.Jira 远程触发 Jenkins 实现更新 GitLab 分支 二、问题 1.Jira 配置网络钩子失败 2. Jira 远程触发Jenkins 报错 一、实验 1.环境 (1)主机 …...

基于SSM的面向TCP_IP的网络互联实验平台
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SSM的面向TCP和IP的网络互联实验平台…...
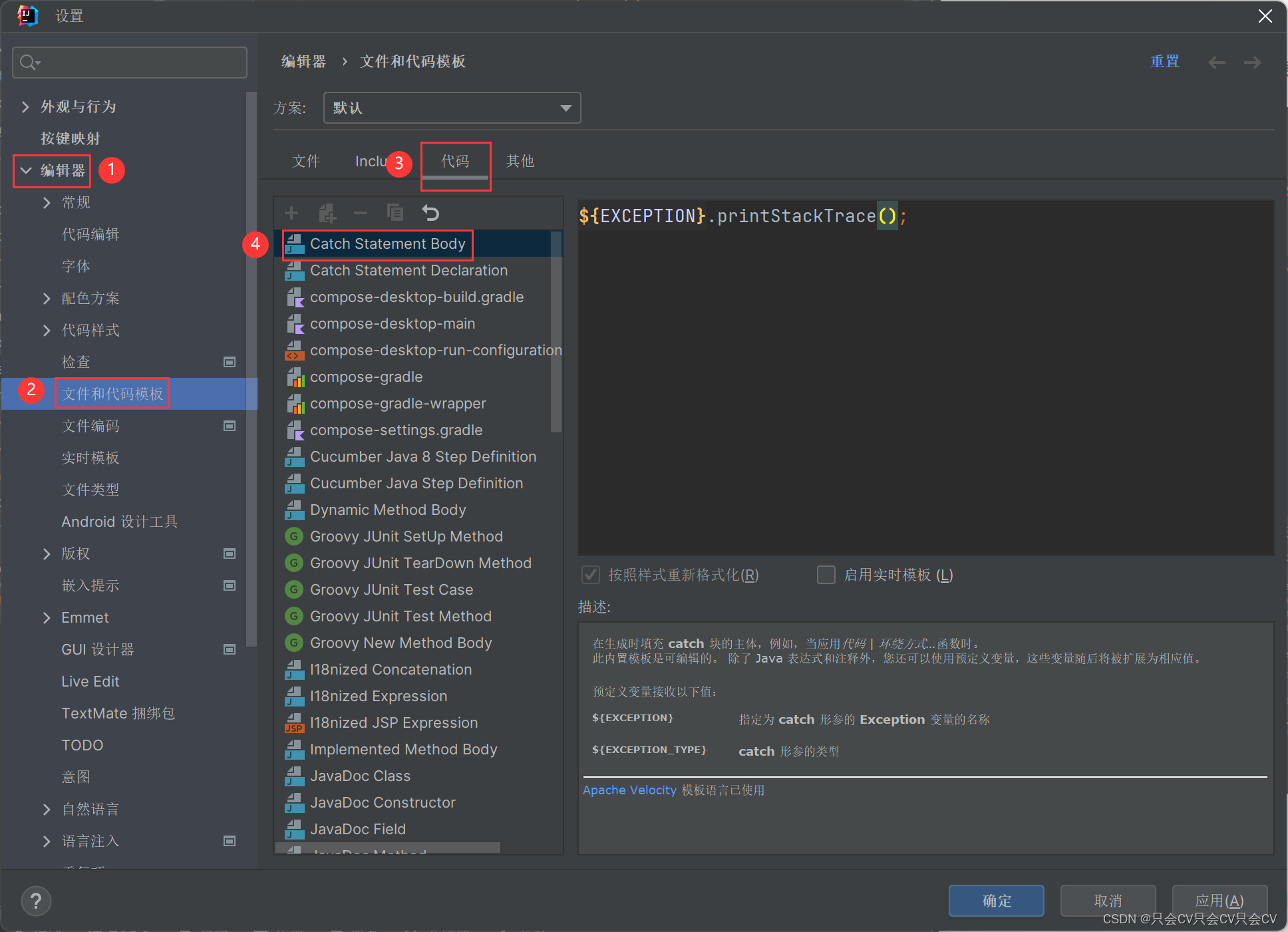
【IDEA】try-catch自动生成中修改catch的内容
编辑器 --> 文件和代码模板 --> 代码 --> Catch Statement Body...

2024 十大AI预测
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
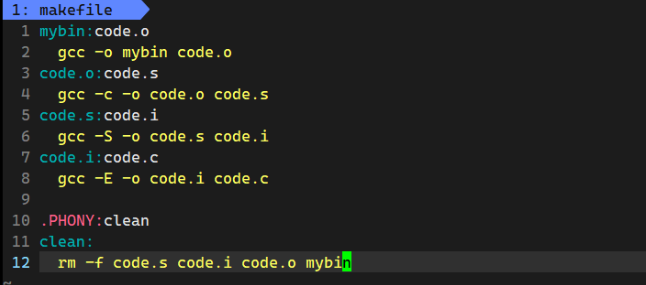
【Linux基础开发工具】gcc/g++使用make/Makefile
目录 前言 gcc/g的使用 1. 语言的发展 1.1 语言和编译器自举的过程 1.2 程序翻译的过程: 2. 动静态库的理解 Linux项目自动化构建工具-make/makefile 1. 快速上手使用 2. makefile/make执行顺序的理解 前言 了解完vim编辑器的使用,接下来就可以尝…...

Windows Nginx版本升级
记录windows系统上nginx版本从1.22.1直接升级到1.25.3,全程一步到位! nginx官网: https://nginx.org/ C:\Windows\system32>cd C:\nginx# 查看当前nginx版本C:\nginx>nginx -v nginx version: nginx/1.22.1# 停止nginx服务C:\nginx>net stop ng…...
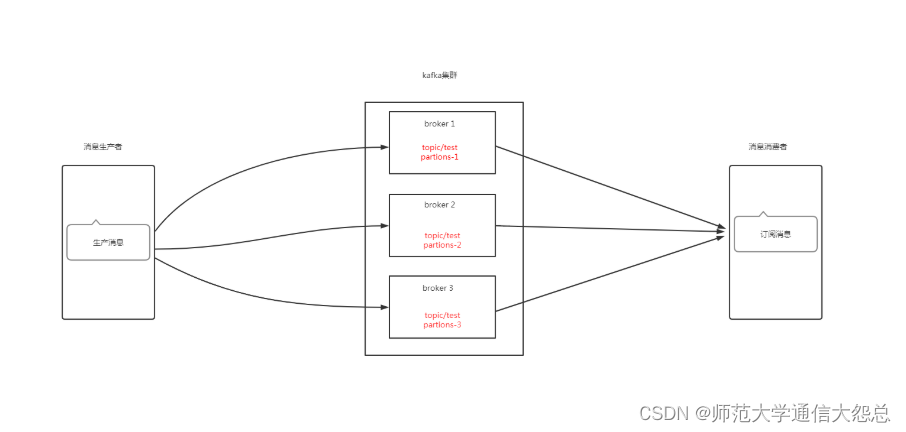
kubernetes集群 应用实践 kafka部署
kubernetes集群 应用实践 kafka部署 零.1、环境说明 零.2、kafka架构说明 zookeeper在kafka集群中的作用 一、Broker注册 二、Topic注册 三、Topic Partition选主 四、生产者负载均衡 五、消费者负载均衡 一、持久化存储资源准备 1.1 创建共享目录 [rootnfsserver ~]# mkdir -…...
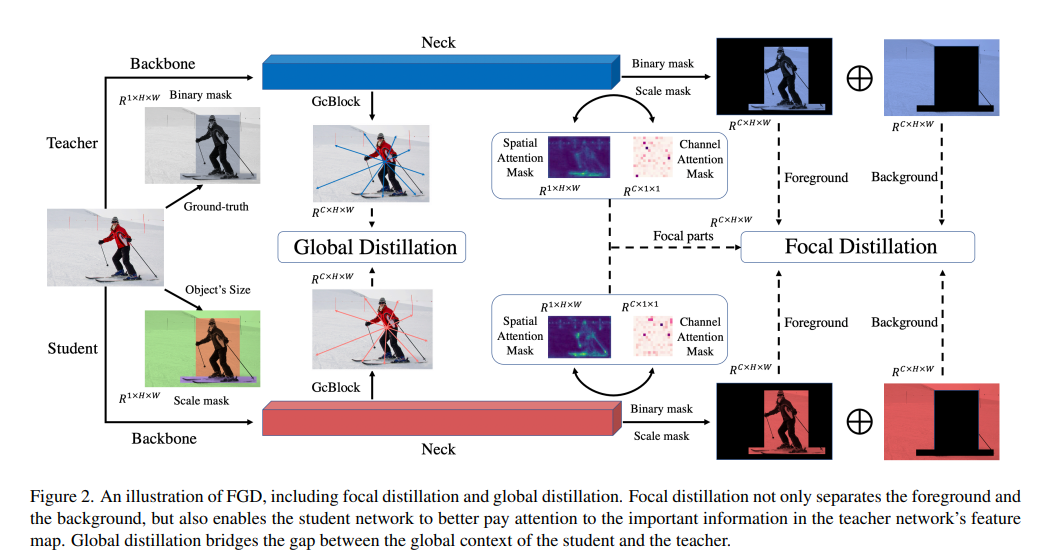
Featured Based知识蒸馏及代码(3): Focal and Global Knowledge (FGD)
文章目录 1. 摘要2. Focal and Global 蒸馏的原理2.1 常规的feature based蒸馏算法2.2 Focal Distillation2.3 Global Distillation2.4 total loss3. 实验完整代码论文: htt...
CentOs 安装MySQL
1、拉取安装包 wget --no-check-certificate dev.mysql.com/get/mysql-community-release-el6-5.noarch.rpm 成功拉取 2、安装 yum install mysql-community-release-el6-5.noarch.rpm 过程中可能需要你同意一些东西,y 即可 然后稍微检查一下 yum repolist enabled…...
基于Java (spring-boot)的在线考试管理系统
一、项目介绍 系统功能说明 1、系统共有管理员、老师、学生三个角色,管理员拥有系统最高权限。 2、老师拥有考试管理、题库管理、成绩管理、学生管理四个模块。 3、学生可以参与考试、查看成绩、试题练习、留言等功能 二、作品包含 三、项目技术 后端语言&…...
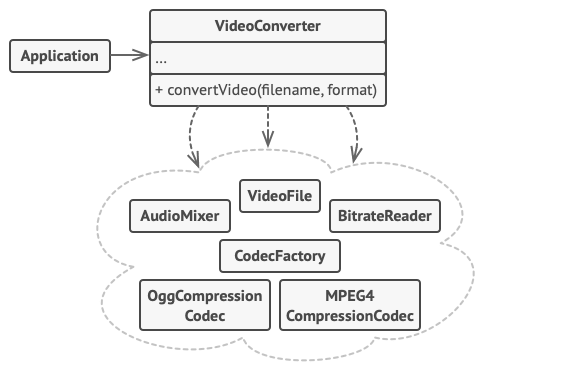
5. 结构型模式 - 外观模式
亦称: Facade 意图 外观模式是一种结构型设计模式, 能为程序库、 框架或其他复杂类提供一个简单的接口 问题 假设你必须在代码中使用某个复杂的库或框架中的众多对象。 正常情况下, 你需要负责所有对象的初始化工作、 管理其依赖关系并按正确…...
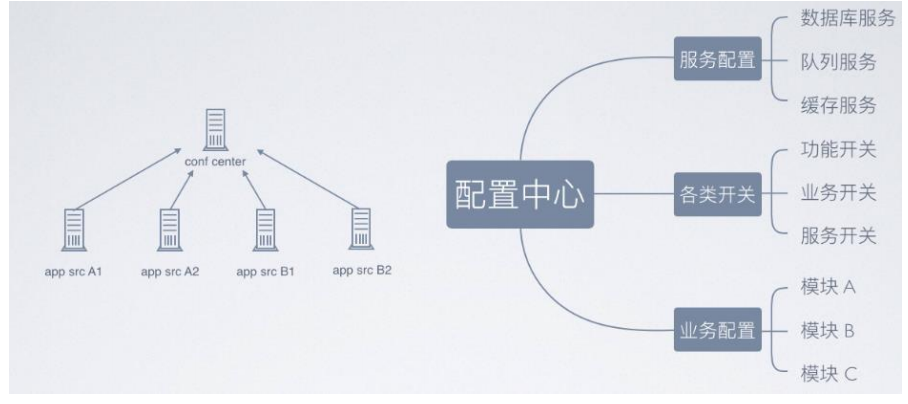
微服务之配置中心与服务跟踪
zookeeper 配置中心 实现的架构图如下所示,采取数据加载到内存方式解决高效获取的问题,借助 zookeeper 的节点监听机制来实现实时感知。 配置中心数据分类 事件调度(kafka) 消息服务和事件的统一调度,常用用 kafka …...

链表 典型习题
160 相交链表:遍历,统计是否出现过 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/ class Solution { public:ListNode *getIntersectionNode(L…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
